Оценка резонансных характеристик однослойных плазмонных сенсоров в жидких средах аппроксимацией Фано в видимом и инфракрасном диапазонах

В последнее десятилетие большое число работ в области нанофотоники было направлено на изучение распространения собственных мод в оптических структурах. Связанные с возбуждением мод резонансные эффекты, такие как усиление электромагнитного (ЭМ) поля и узкие резонансные линии в спектрах, представляют большой интерес как для фундаментальных, так и для прикладных исследований.

Возбуждение мод поверхностных плазмон-поля-ритонов (ППП), поддерживаемых металло-диэлектрическими слоистыми структурами, приводит к появлению резонансных линий в пространственных спектрах нарушенного полного внутреннего отражения (НПВО) [1]. Чувствительность резонансного отклика к изменениям оптических характеристик внешней среды широко используется в сенсорных устройствах для определения качественных и количественных изменений среды, а также низких концентраций веществ, адсорбированных на поверхности [2–6].

Исследования по усилению ближнего поля и резонансных явлений, возникающих на границе металлдиэлектрик, важны для различных применений, например, для создания наноразмерных локальных источников света или создания управляемых одиночных плазмонов в интегральных оптических схемах, усиления и затухания флуоресценции одиночных молекул, расположенных вблизи металлической поверхности. Существенный интерес вызывает исполь- зование резонансных эффектов плазмонных структур в сенсорике инфракрасного (ИК) диапазона для возбуждения колебательных мод молекул органических соединений [7–10]. ИК-диапазон содержит важную информацию о молекулярном строении веществ, поскольку колебательные моды молекул, резонансно возбуждаемые ИК-излучением, непосредственно связаны с элементами молекул, их химическими связями и их конфигурацией, что делает ИК-спектроскопию мощным и необходимым инструментом. В частности, ИК Фурье-спектроскопия широко используется в различных областях исследований и в индустрии. Однако вследствие низкого молекулярного поглощения в ИК-диапазоне требуются достаточно большой объём материала и применение громоздкого и дорогого чувствительного оборудования. Исследования в области поверхностно-усиленной ИК-спектроскопии, в основе которой лежит резонансное усиление ближнего поля и, как следствие, усиление поглощения света детектируемыми молекулами, направлены на преодоление этих ограничений.

Моды ППП в видимом диапазоне характеризуются большими энергетическими потерями, связанными с поглощением в металле. Вследствие низкой добротности, широкие резонансы были обнаружены в прошлом веке в спектрах НПВО слоистых планарных плазмонных структур в конфигурациях Отто [11] и Кречмана [12]. Авторами были проведены расчёты и анализ резонансных характеристик мод ППП трёх- слойных структур в водной среде в конфигурации Кречмана в рамках ЭМ теории на основе матричного метода 2×2 [13] в ультрафиолетовом (УФ), видимом и ближнем ИК-диапазонах (до 2000 нм) [14]. Было выявлено повышение максимальной чувствительности и усиление поля на поверхности сенсорных структур в ближнем ИК-диапазоне для серебра (Ag), алюминия (Al), золота (Au) и меди (Cu).

Однако необходимость расчётов пространственных спектров и их последующей обработки для получения характеристик резонансных линий и поля приводит к громоздким и ресурсоёмким вычислениям.

В недавней работе авторов [15] были получены аппроксимации формулой Фано асимметричных резонансных линий в пространственных спектрах НПВО двуслойных и трёхслойных плазмонных структур в конфигурациях Кречмана и Отто. Аналитическое представление коэффициентов аппроксимаций Фано и усиление поля моды на поверхности структуры найдено на основе ЭМ теории и теории связанных мод. Показано, что такие характеристики резонансного отклика, как ширина, высота, сдвиг резонанса, могут быть выражены с использованием коэффициентов, выражения которых получены аналитически.

В настоящей работе проводится анализ резонансных характеристик отклика мод ППП и чувствительности трёхслойных структур в конфигурации Кречмана на основе аппроксимации резонанса Фано для жидких сред на основе воды, этанола, изопропанола в видимом, ближнем и среднем ИК-диапазонах. В расчётах рассматриваются плазмонные структуры на основе Ag, Al и Au.

1.    Описание численного эксперимента

Исследуемая в численном эксперименте структура изображена на рис. 1. Она используется в известных техниках возбуждения затухающими волнами мод ППП в планарных структурах при условиях НПВО. В конфигурациях Отто [11] и Кречмана [12] генерация затухающих волн происходит в среде с низким показателем преломления при падении луча в высокоиндексной призме на их границу раздела под бóльшим углом, чем критический угол. При этом затухающие волны генерируются как в слое металла, так и в слое детектируемой среды, что приводит к возбуждению моды ППП на границе раздела сред металл-диэ-лектрик. Эти конфигурации НПВО на основе планарных структур отличаются простотой изготовления и использования. Так, конфигурацию Кречмана можно представить как трёхслойную структуру, включающую полубесконечный слой высокоиндексного непоглощающего диэлектрика L 0 с показателем преломления n 0 , металлический слой L 1 конечной ширины h с комплексным показателем преломления n 1 и полубес-конечный диэлектрический слой L 2 с комплексным показателем преломления n 2 , представляющий собой детектируемую среду.

Распространяющаяся в L 0 монохроматическая p -по-ляризованная плоская волна H ( x , z )= u exp[i k 0 ( α x + β i z )]

падает на границу раздела I01 слоев L0 и L1 под углом θ к её нормали, k0 =2π / λ0 – волновое число падающего излучения с длиной волны λ0 в свободном пространстве, u – комплексная амплитуда волны. Для случая распространяющейся волны (α2 < ε0) константа распространения волны вдоль оси x (рис. 1) находится как k0α= k0ε0sinθ. Константа распространения падающего излучения вдоль оси z в i-м слое будет определяться как k0βi=k0εi-α2 , где εi= ni2 – диэлектрическая проницаемость слоя Li. В условиях НПВО α >Re n1, Re n2, где Re обозначает действительную часть комплексного числа, β1 и β2 имеют ненулевую мнимую часть. При этом амплитуда волн экспоненциально затухает в слоях L1 и L2 вдоль оси z при удалении от границы I12, и такие волны относятся к затухающим волнам.

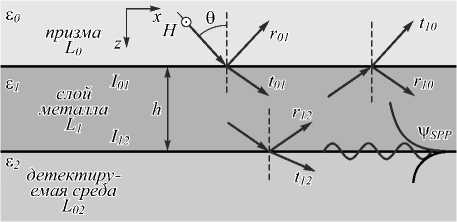
Рис. 1. Возбуждение моды ППП в конфигурации Кречмана

Распространение моды ППП вдоль границы I 12 возможно в случае, если действительные части диэлектрических проницаемостей слоев L 1 и L 2 удовлетворяют условиям ε ₁ ′ ε ′ ₂ <  0, ε ₁ ′+ ε ′ ₂ < 0, | ε ′ ₂ | > | ε ₁ ′ |. Поле моды ППП в слое L j может быть представлено в виде ψ ( x , z )= ψ j ( z ) exp(i γ SPP k 0 x ), где ψ – комплексная амплитуда моды ППП, ψ j = ψ exp(– b j | z |), b j = [ - ε 2 j /(ε 1 + ε 2 )]1 ' 2 , k 0 γ SPP – константа распространения моды ППП вдоль границы I 12 , j = 1, 2. Константа распространения моды вдоль оси x, нормированная на k 0 , γ SPP может быть интерпретирована как эффективный показатель преломления моды, характеризующийся отношением скорости света к фазовой скорости моды. Для границ раздела сред металл-диэлектрик с комплексными диэлектрическими проницаемостями ε 1 и ε 2 выражение для комплексной нормированной константы распространения γ SPP = γ S ′ PP + iγ S ′′ PP моды ППП находится как [1]:

γ SPP ⁼

ε 1 ε 2 ε 1 +ε 2

где γ ′ SPP соответствует фазовой скорости моды ППП, γ ′ _S ′ _PP – коэффициент затухания моды ППП.

ЭМ поле затухающей волны генерирует моду ППП, распространяющуюся вдоль границы I12. Амплитуда поля моды ППП максимальна на границе I12 и экспоненциально убывает с расстоянием от границы раздела в обеих средах и исчезает при |z| → ∞, как схематично изображено на рис. 1. В акустике такие поверхностные волны классифицируют как неоднород- ные [16]. В условиях возбуждения моды ППП часть энергии поглощается, а часть отражается в слой L0. Энергия, перешедшая в моду ППП, приводит к резонансу в угловом спектре отражательной способности. При этом зависимость отклика поля моды ППП, как дискретной моды, от нормированной константы распространения падающей волны а характеризуется асимптотическим резонансным поведением (ySpp - а2)-1 [17]. Угол, на котором наблюдается минимум интенсивности отражённого света в пространственных спектрах, называется резонансным и обозначается Ores. Резонансному углу соответствует значение нормированной константы распространения падающей волны αmin.

В общем случае коэффициент отражения r 012 трёхслойной структуры находится как [1]

где r012

r 01 + r i2 V 2

1 + r 01 ^2 ,

r ij

P / A^-B z /^L в/ё ⁺ Р у /е у

коэффициент отражения для границы раздела слоев L и L j в случае падения p -поляризованной волны из слоя L, v = exp( ik ₀ р 1 h ) - коэффициент затухания ЭМ поля в слое L 1 .

Ранее мы показали, что в случае двуслойной структуры металл-диэлектрик в области резонанса а ^ Y sPP интерференция резонансной компоненты отражённого поля, возникающей вследствие возбуждения моды ППП, и нерезонансной компоненты приводит к возникновению асимметричных резонансных линий Фано в пространственных спектрах коэффициента отражения r ₁₂ [15]. Аппроксимация r₁₂ коэффициента отражения r 12 на границе I 12 может быть получена для Y s_PP ^ Y S_PP или Y s_PP ^ 0 в виде

• - с ^{а   Y} zero

Г12 = r 2----=---, а - Ypole где с е2 - е,   е, + е2 ySpp r12 =-------+-- е1 + £2   е2 - е1 а2

коэффициент нерезонансного отражения от границы раздела слоев L 1 и L₂, y _pole = Y SPP - полюс и Y z_ero = Y SPP + Р 12 / r 2 — ноль аппроксимации r ₂ для двуслойной структуры, p ₁₂ = 2y S_pp / (е ₂ - е 1 ) - амплитуда моды ППП.

Для трёхслойной структуры Фано аппроксимация полного коэффициента отражения r012 может быть получена подстановкой аппроксимации (3) коэффициента отражения r12 в выражение (2) в виде произведения медленно меняющегося континуума и резонансной компоненты r012

= c ^{а Y}zero ⁰¹² а - Y pole ,

где r0c12

Г о1 + r 2 V 2 1+ r 01 r ₁ ^с ₂ v²

коэффициент нерезонансного отражения трехслойной структуры. Аналитические выражения для полюса и ноля резонансной компоненты функции Фано (4) могут быть найдены для Y sPP >>  Y sPP в виде [15]

Y pole = (Y SPP + Ь )^V 2 ,                                      (5)

Y zero = Y pole ^{+ (} a ^{- b} ) Y pOle /² ,                             ⁽⁶⁾

соответственно, как результат, где a = 2y spp V ² P 12 ( r „ + r 12 v² ) ^{- 1}, b = 2Y spp r >1 V² P 12 (1 + r >1 r 2 v²) ^{- 1}.

Таким образом, отражательная способность трёхслойной структуры | r 012 |² описывается аппроксимацией Фано

I r 01₂|2

= | ^r 0 c 12 I

γ zero       γ zero

^{(а -} Y pole^{) 2 +} Y^ le

где Yzero = Yzero + iYzero, Ypole = Ypole + iYpole . С помоЩЬЮ параметров Фано аппроксимации a, b, ypole и yzero возможно провести оценку таких характеристик формы линии ППП резонансов, как ширины резонанса на полувысоте (FWHM), высоты резонанса, положения резонанса в пространственном спектре Ores, усиления поля.

В рамках аппроксимации формулой Фано ширина резонанса на полувысоте Г вычисляется как

^Г = 2 ^YSPP^YSPP + b . ⁽⁸⁾

В соответствии с выражением (8), ширина резонанса в первом приближении прямо пропорциональна потерям в слоях L 1 и L 2 . Пространственные спектры отражательной способности, полученные экспериментально, являются зависимостями от угла падения θ падающей волны и выражаются в градусах. В этом случае может быть определена необходимая для измерений угловая точность оптической установки. Учитывая а = ^/ё О" sin 9 , выражение для FWHM, выражаемой в градусах, примет вид:

FWHM = _8 ⁰_ ( n о² - y z^o ) 2Г. (9) π

Условие возможности возбуждения моды ППП в рассматриваемой трёхслойной структуре формулируется на основе выражения (9) в виде ограничения на выбор показателя преломления призмы n ₀ >  Y zero ■

Возбуждение моды ППП на границе I 12 сопровождается усилением ближнего поля. На основе теории связанных мод можно записать усиление магнитного поля FE = | ^ ( z )|²/| z |² на I₁₂ в виде [15]

FE = |v 1 01 Р 12 1²/ lYp^le] ². (10)

Здесь коэффициент пропускания t 01 = r 01 + 1 для случая падения плоской волны в слое L 0 на границу раздела сред I 01 .

Трёхслойные резонансные плазмонные структуры нашли множество применений в детекции окружающей среды. Резонансы в спектрах отклика сенсорных структур меняются в зависимости от характеристик окружающей сенсор среды, например, растворов или газов [18]. Одной из важных характеристик сенсора является его чувствительность S y = A y / A x к изменению характеристики x , выраженная как отношение изменения A y = y - у 0 выходной величины у 0 сенсора вследствие изменения A x = x - x 0 детектируемой характеристики x 0 , где x и y – значения изменённых входной детектируемой характеристики и выходного параметра сенсора соответственно [5]. Если входным параметром оптического сенсора является показатель преломления детектируемой среды, то рефрактометрическая чувствительность характеризует изменение выходного параметра сенсора, вызванное изменением показателя преломления детектируемой среды. Выходным параметром оптических сенсоров могут быть резонансный угол O res , резонансная длина волны X _res, интенсивность отражённого света. В зависимости от вида выходного параметра чувствительность оптических сенсоров подразделяется на соответствующие типы. Так, при измерении интенсивности отражённого света I( 0 , X ) = | r ₀₁₂( 0 , Х )|², детектируемого при некотором угле падения (отражения) θ и некоторой длине волны X , выходным параметром сенсора является интенсивность. Рефрактометрическая чувствительность сенсора в этом случае может быть записана в следующем виде:

S I ( е,Х ) = |А 7 ( е,Х ) /А n 2| . (11)

Угловая рефрактометрическая чувствительность определяется как отношение величины сдвига AO res резонансного угла O res вследствие изменения A n 2 показателя преломления детектируемой среды n 2 :

S е = | Аe res / А n 2] . (12)

В случае трёхслойной резонансной структуры чувствительность положения резонанса в спектре по нормированной константе распространения S _у может быть определена как отношение изменения положения нуля Y Zero функции Фано (5), вызванного изменением показателя преломления n 2 :

S Y = |AY Zero / А n 2] . (13)

Учитывая, что e _res ® arcsm^ Zero / n ₀ ), угловая рефрактометрическая чувствительность может быть вычислена через параметры аппроксимации по формуле:

S е = S _Y ( n 02 - Y Z2ro ) -^Ш180 ° /п. (14)

Чтобы подчеркнуть тип рефрактометрической чувствительности и ввести отличие безразмерных величин, входящих в выражения чувствительности, для единиц показателя преломления детектируемой среды n 2 вводится обозначение RIU ( refractive index units ) [5].

Характеристика чувствительности (FOM) сенсора на основе резонанса ППП, дающая оценку снизу максимальной рефрактометрической чувствительности по интенсивности max S I ( е,Х ) , определяется как:

, I Г 012 ( a max )| ² - r 012 ( a m, )| ²

FOM ( е,Х ) = S _YJ_г^, (15) где a _max и a _min - положения максимума и минимума отражательной способности трёхслойной структуры, рассчитываемые как положения экстремумов первой производной выражения (7).

2.    Численные результаты

Для численного моделирования резонансных характеристик однослойных сенсорных структур рассматривались следующие параметры. В расчётах по-лубесконечный слой L 0 представляет собой высокоиндексную призму из материала ZnSe с показателем преломления n 0 [19], обладающую низким поглощением от зелёной части видимого диапазона до среднего ИК-диапазона. В вычислениях поглощение призмы считается малым, и n 0 принимает только действительные значения. Значения показателя преломления n 1 слоя L 1 соответствовали таким плазмонным материалам, как Ag и Au [20], Al [21]. В качестве материалов полубесконечного слоя L 2, представляющего собой детектируемую среду, с показателем преломления n 2 рассматривались вода [22], растворы 99,9 % этанола и 99,8 % изопропанола [23].

Вычисление ширины резонанса на полувысоте проводилось на основе выражения (9), FOM – на основе (16), усиления поля – на основе (10). Расчеты проводились для значений длин волн в диапазоне прозрачности ZnSe от 500 до 10000 нм с шагом 10 нм для различных значений толщины h слоя металла L 1 в диапазоне от 1 до 100 нм с шагом 1 нм. Зависимости максимальных значений FOM, достигаемых для оптимальных значений h opt толщины слоя металла, от длины волны приводятся на рис. 2. Чувствительность положения резонанса численно оценивалась по формуле (14) с использованием формулы (13) для изменения действительной части показателя преломления A n 2 = 10 -6 RIU.

Для некоторых значений h и X рассчитываемые коэффициенты принимают значения, приводящие к нефизичной интерпретации результатов. Так, действительные части коэффициентов ySPP, Ypole, YZero могут принимать значения меньше n2. В этом случае возбуждение моды ППП на границе I12 невозможно, и эта серия расчётов не принимается во внимание. В соответствии с формулами (5) и (6) корректные значения коэффициентов достигаются при h > 5 нм для Al и h > 10 нм для Ag и Au. В расчетах рассматриваются серии, для которых положение полюса Ypole = amax аппроксимации Фано лежит на шкале левее относительно значения её нуля YZero = amin в соответствии с выражениями (5) и (6). Серии, для которых |ro12(amin)|2 > 1, |ro12(amax)|2 < |ro12(amin)|2, являются нефизичными и не рассматриваются. Кроме того, не рассматриваются серии, для которых усиление поля моды ППП FE< 1,0. Для расчетов угловой ширины резонанса с учетом показателя преломления призмы n0 коэффициенты, описывающие положение минимума резонанса, должны удовлетворять условиям Yzero , amin < n0 .

а)

б)

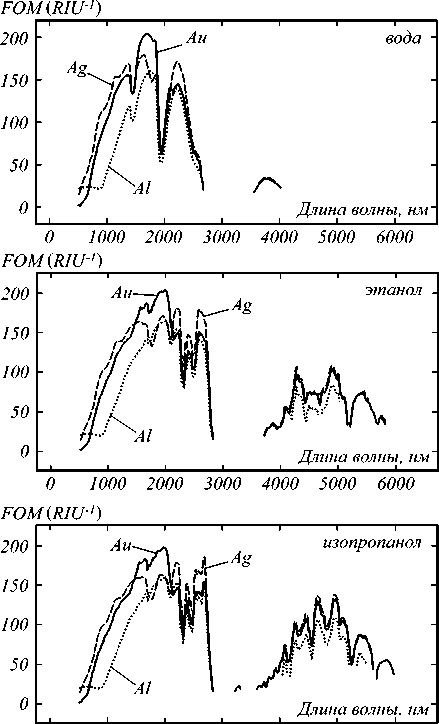
Рис. 2. Зависимость оценки чувствительности FOM от длины волны для структур в средах воды (a), этанола (б), изопропанола (в)

в)

В спектрах FOM наблюдаются три области с высокими значениями. Чувствительность сенсорных структур возрастает с возрастанием длины волны со значений около 20 RIU-1 при 500 нм до значений 150–200 RIU-1 на длинах волн от 1500 до 1900 нм для воды и до 2300 нм для этанола и изопропанола. В случае детекции воды области высоких значений FOM около 170 RIU-1 наблюдаются в диапазоне 1500 – 1900 нм, около 150 RIU-1 наблюдаются в диапазоне 2000 – 2500 нм, около 30 RIU-1 наблюдаются в диапазоне 3500–4000 нм. В случае детекции этанола и изопропанола первый диапазон высокой чувствительности расширяется по сравнению с детекцией воды до 2100 нм, средний диапазон сдвигается к 2200– 2700 нм, третий диапазон значительно расширен от 3500 до 6000 нм со средними значениями чувствительности 75– 100 RIU-1. Поглощение в детектируемых средах вызывает ослабление и исчезновение чувствительности в областях 2000 нм, 2800–3500 нм и более 4000 нм для воды, в областях 2800–3600 нм и более 6000 нм для этанола, в областях 2900– 3600 нм и более 6100 нм для изопропанола.

Структуры на основе Ag и Au показывают близкие значения чувствительности, большие значений структур на основе Al на 20–30 %.

Значения оптимальных толщин h opt слоя металла трёхслойной структуры, для которых оценки чувствительности FOM являются максимальными, показаны на рис. 3 как функции длин волн. Оптимальные толщины близки для случаев детекции рассматриваемых растворителей. Вариации наблюдаются для воды на длине волны усиления поглощения воды около 2000 нм.

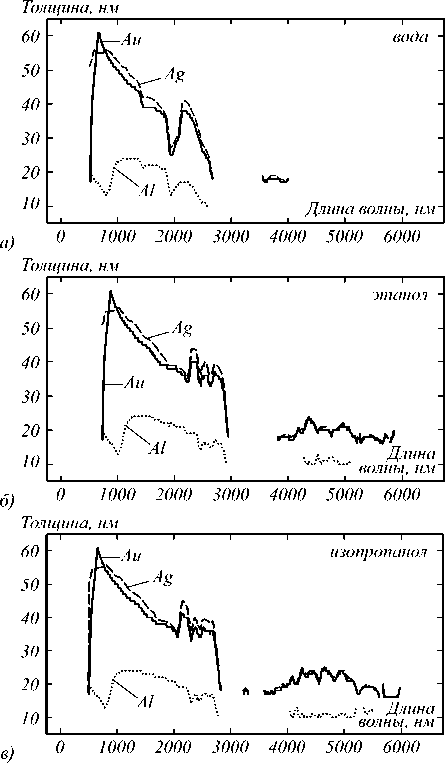
Рис. 3. Зависимости оптимальных толщин слоя металла от длин волн для максимизации FOM структур в средах воды (a), этанола (б), изопропанола (в)

Близкие значения оптимальной толщины Au и Ag возрастают от 20 нм при длине волны 500 нм до 55 – 60 нм при длине волны 650 нм и спадают до 20 нм при увеличении длины волны. Вариации толщины для Al происходят в диапазоне от 10 до 22 нм, что объясняется большей величиной абсолютной действительной части диэлектрической постоянной Al.

Для найденных значений оптимальных толщин h opt были рассчитаны зависимости значений FWHM в спектрах от длины волны, приведённые на рис. 4.

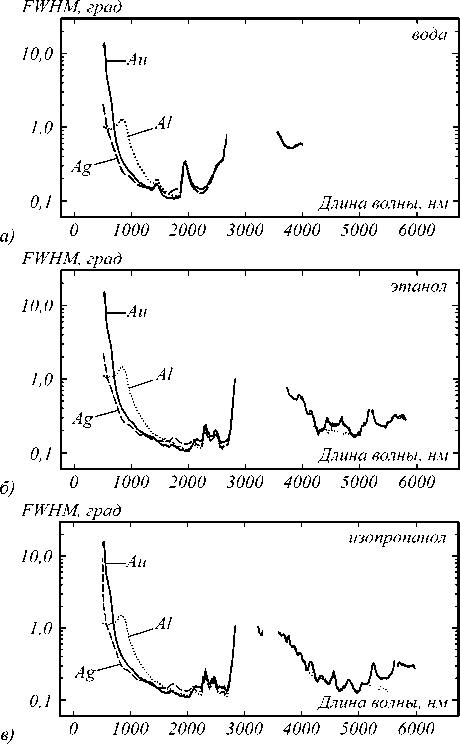
Рис. 4. Ширина на полувысоте ППП резонанса в спектрах структур на основе Ag, Au и Al в средах воды (a), этанола (б), изопропанола (в)

При увеличении длины волны от 500 нм FWHM уменьшается со значений 10° в случае Au, 2° в случае Ag и 1° в случае Al до около 0,1° при длине волны около 1800–2000 нм для всех рассматриваемых металлов.

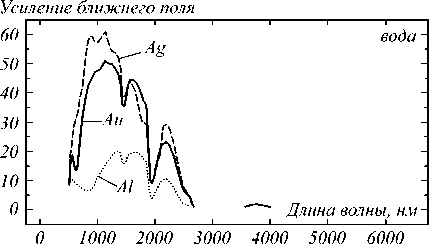
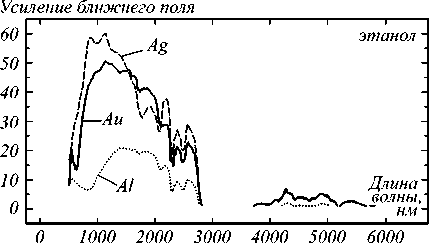
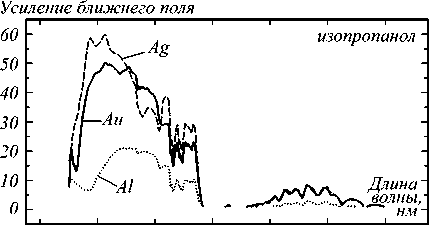
Значения максимального усиления ближнего поля на границе I 12 , рассчитанные с помощью выражения (10) для заданных длин волн, достигаются при толщинах слоя L 1 , отличных от h opt . Таким образом, резонансная структура, оптимизированная для получения максимального усиления поля моды ППП на границе I 12 , не проявляет максимальную чувствительность. Области максимального усиления поля на поверхности структуры, зависимости значений которого от длины волны представлены на рис. 5, составляют около 60 в диапазоне 900– 1100 нм для Ag, около 50 в диапазоне 1000 – 1100 нм для Au и около 20 в диапазоне 1300 – 1600 нм для Al. В среднем ИК-диапазоне наблюдается максимальное усиление моды ППП около 2 в случае водной среды в диапазоне 3500–4000 нм для всех металлов, в случае этанола и изопропанола – около 3–5 в диапазоне 3500–6000 нм.

Увеличение FWHM до 0,2°–0,3° наблюдается около 2000 нм в случае детекции воды и в диапазоне 2300– 2500 нм в случае детекции этанола и изопропанола вследствие повышения поглощения в этих растворите- лях. В диапазоне 2700–3500 нм для всех растворителей наблюдается деградация резонанса. Резонанс шириной около 0,7°, что достигается для красного видимого диапазона, может быть также получен и в диапазоне 3500– 4000 нм в случае воды. Для среднего ИК-диапазона в случаях этанола и изопропанола значения ширины 0,1°– 0,3° достигаются в диапазоне 4000–6000 нм. Al показывает большую ширину резонанса в ближнем ИК-диапазоне по сравнению с Ag и Au. В среднем ИК-диапазоне (более 3000 нм) значения ширины близки для всех рассматриваемых металлов.

а)

б)

О 1000 2000 3000 4000 5000 6000

Рис. 5. Зависимости максимального усиления ближнего поля на поверхности металла в средах воды (a), этанола (б), изопропанола (в)

в)

В области длин волн от 4000 до 6000 нм величины усиления поля близки для структур со слоями Ag и Au. Структуры со слоем алюминия демонстрируют меньшие величины усиления поля на всем рассматриваемом диапазоне длин волн.

Заключение

В работе продемонстрировано, что плазмонные сенсоры в конфигурации Кречмана на основе одного слоя Ag, Au или Al в средах воды, этанола и изопропанола проявляют в 6 раз большую чувствительность, в 10 раз более узкий резонанс в ближнем ИК-диапазоне по сравнению с длиной волны 632,8 нм.

Усиление поля на поверхности сенсора на основе Ag или Au достигает в 3 раза больших значений, чем для сенсоров на основе Al. В среднем ИК-диапазоне применение водных сред в сенсорике ограничено областью относительно низкого поглощения воды 3500 – 4000 нм. Расширение области детектирования в жидких средах до 3500–6000 нм возможно с использованием этанола и изопропанола. Полученные результаты могут быть применены для разработки и оптимизации высокочувствительных сенсоров на основе слоистых плазмонных структур для ИК-диапазона.

Работа выполнена при поддержке Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части постановки задачи численного эксперимента, РНФ (проект № 19-19-00514) в части реализации численных экспериментов и Российского фонда фундаментальных исследований (грант 18-29-20006) в части численных результатов.