Оценка результатов многократных измерений с использованием функций распределения вероятности с переменным масштабом

Одним из способов повышения точности и надежности результатов измерений физических величин является проведение многократных измерений с последующей статистической обработкой. Для проведения обработки по полученным результатам измерений строится функция распределения вероятности некоторого вида и определяются ее числовые характеристики. Полученные характеристики являются основанием для представления измеренной величины в виде х о ± Ах , где х о определяет центр интервала, в котором может лежать истинное значение измеряемой величины, а Ах — абсолютную ошибку измерений.

В настоящее время для статистической обработки используется в основном оценка по среднему арифметическому значению выборки с использованием центрального момента второго порядка (дисперсии) для определения абсолютной ошибки. Оценка по среднему арифметическому является общепризнанной методикой обработки результатов многократных измерений, однако ее использование следует считать корректным только для симметричных распределений случайных величин. Практически чаще всего используют гауссовское (нормальное) распределение, хотя, как показывают исследования, отнюдь не абсолютное большинство измерительных процессов дают распределение результатов измерений, подчиняющееся этому закону [1, 2]. Способы же оценки интервала распределения (например, по центральным моментам различного порядка) зависят от конкретного вида закона распределения.

Следует заметить, что метод обработки результатов измерений оказывается привязанным к конкретному закону распределения, предполагаемому априорно или определенному в процессе исследования характеристик измерительного прибора или системы. Однако при практических измерениях довольно часто наблюдаются отклонения закона распределения полученной выборки от предполагаемого вида распределения. Это может быть связано как с промахами, так и с объективными флуктуациями измеряемых значений, особенно при малых объемах выборки.

Существенные отклонения математического ожидания выборки от действительного значения измеряемой величины при наличии в выборке промахов обусловливают необходимость использования дополнительных методов фильтрации входных данных, либо использования альтернативных методик оценки (например, по медиане или моде выборки) [3]. Эти методики, как правило, носят индивидуальный характер, и не могут быть однозначно рекомендованы для проведения обработки результатов измерений различных физических величин. В связи с этим существует необходимость создания метода обработки результатов многократных измерений, устойчивого к наличию промахов в исходных данных, позволяющего использовать различные законы распределения и допускающего автоматизацию процесса обработки.

ПОСТАНОВКА ЗАДАЧИ

Задача статистической обработки результатов измерений может быть сформулирована следующим образом. Пусть события X1, X2,..., XN соответствуют состояниям хист = х 1, хист = х2 и т.д. Пусть также в результате измерений были получены события A।, A2,..., Am, соответствующие состояниям хизм = а 1, хизм = а2 и т.д. На основании этих данных требуется оценить вероятности событий X1, X2,.., XN, определить наиболее вероятное значение измеряемой величины и оценить погрешность измерений. При этих условиях апостериорная (после-опытная) вероятность событий X1, X2,..., XN может быть использована для оценки истинного значения хист измеряемой величины. Определение апостери- орной вероятности осуществляется в соответствии с теоремой Бейеса:

P ( ХДА ) = , P ⁽ AX k ) ^{P (} ,        (1)

S p (Ax,) p (xj i=1

где P(X k lA) — апостериорная (послеопытная) вероятность гипотезы X k при условии, что произошло событие A ; P(AX k ) — условная вероятность появления события A при наличии гипотезы X k ; P(X k ) — априорная вероятность гипотезы X k .. Или для непрерывных случайных величин:

, _ч     f ( x ) P ( A\x )

• f, ( x ) = +,              ,            (2)

J P (Ax)f (x )dx

-, где f A (x) — плотность распределения вероятности x по A .

Поскольку в теореме Бейеса не вводится ограничений на количество произведенных измерений m , можно ожидать, что и при малых m будет получена адекватная оценка вероятности гипотез. Однако основным препятствием к использованию теоремы Бейеса является недостаточно обоснованная оценка априорной вероятности гипотез X_i при проведении конкретных измерений. Действительно, в выражениях (1), (2) оказываются неизвестными как априорные вероятности появления того или иного истинного значения измеряемой величины, так и условная вероятность появления соответствующих показаний прибора. И если априорные вероятности появления гипотез относятся к анализируемым объектам, то вероятность появления тех или иных показаний измерительного прибора является характеристикой измерительной системы. На практике можно определить функцию распределения вероятности погрешности, вносимой измерительной системой, однако использование такой функции имеет смысл лишь при достаточно большом объеме выборки, когда вероятностные характеристики результатов измерений будут приближаться к истинным. Кроме того, наличие промахов в выборке ограниченного объема приводит к существенному отклонению параметров полученного распределения от истинного значения измеряемой величины. Таким образом, функция распределения вероятности, получаемая на основе ограниченной выборки, не всегда адекватно отражает реальные характеристики процесса измерений.

ПРЕДЛАГАЕМОЕ РЕШЕНИЕ ЗАДАЧИ

Рассмотрим процесс определения функции распределения вероятности более подробно. Часто вид этой функции может быть качественно опре- делен исходя из структуры и особенностей конструкции измерительной системы. Однако конкретные числовые характеристики могут существенно варьироваться от одной серии измерений к другой. Для их точного определения требуется достаточно большой объем выборки, получение которого связано с длительным временем на проведение многократных измерений. Кроме того, при таком подходе требуется отдельная фильтрация промахов.

В данной работе для оценки апостериорной вероятности гипотез предлагается рассматривать функцию P(A/X k ) в некотором диапазоне значений ее дисперсии (масштаба). Построение для каждого из выбранных значений дисперсии функции распределения вероятности позволит получить апостериорную вероятность гипотез как функцию двух величин — X_k и масштаба ст

P ( X k ) = f p ( X „ , ст ) , (3)

где f_P(X_k, ст) — некоторая функция двух переменных, имеющая смысл вероятности.

Проанализируем особенности данного подхода на примере нормального распределения ошибки измерений. Предполагается, что истинные значения контролируемого параметра объектов исследования равномерно распределены в рабочем диапазоне измерительной системы, т.е. невозможно априорно указать наиболее вероятное истинное значение измеряемого параметра.

Априорная вероятность появления показаний прибора x k при условии, что истинное значение измеряемой величины равно x ист , описывается некоторой функцией распределения вероятности. Вид этой функции зависит от методики проведения измерений и конструкции прибора и может быть качественно оценен на этапе разработки и испытаний измерительного прибора. Например, при нормальном (гауссовском) законе распределения условная вероятность появления тех или иных показаний прибора определяется как

⁽ x k ^- x _и ст )

• ^{d P (} x k x ист ) = "A^e 2 ^{СТ 2} d x • ⁽⁴⁾

• V 2пст

В формуле (4) присутствует параметр ст , определяющий дисперсию ст ². Этот параметр является уникальной числовой характеристикой каждой конкретной выборки и зависит прежде всего от условий проведения измерений, варьирующихся от одной серии измерений к другой. Таким образом, в (4) оказывается неизвестным параметр, характеризующий разброс результатов измерений.

Анализ вероятности гипотез предлагается производить при различных значениях дисперсии (или иного параметра, характеризующего разброс результатов). Выбирая значения дисперсии в некотором интервале, можно получить вероятности гипотез X1, X2,..., Xn как функцию двух переменных — значения xk и масштаба а.

Тогда в соответствии с теоремой Бейеса оказывается возможным определение апостериорной вероятности гипотезы X_k : x _ист = x_k в соответствии с (1) или (2). При условии, что априорные вероятности событий являются функциями дисперсии, получаем:

f ⁽ х ) P ( X k\ x ист , а )

A (х,а )=^

J P ^{( х}к|^х ист , ^а ) f ⁽ x ^{) d x}

-те

Табл. 1. Значения случайно распределенной величины

Номер измерения	Значение случайно распределенной величины
1	40
2	50
3	60

Поскольку было сделано предположение, что появление объектов с теми или иными свойствами равновероятно, можно считать f ( х ) = const и (5) принимает вид:

^{f ( х} ) ^{P (} x k l x ист , ^а )

A (x, а )= ----■*-----— f (x )J P (xk\x ист ,а )dx

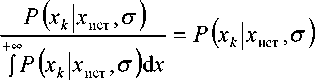
-те

(последнее преобразование было сделано с учетом +те того, что JP(Хк|хист,а)dx = 1).

-те

Наконец, для серии измерений A 1 , A 2 ,... , A m , воспользовавшись формулой сложения вероятностей, получаем

1N fA (Х,а )= N 5P(х/|хист , а ).         (7)

Аналогично, для серии измерений при условии, что f ( х ) ^ const, (5) может быть записано в виде

£ / ( х ) P ( X k x ист , а )

/а ( х - а ) = N +S .      (8)

J ^P ( Тк|^х ист , ^а ) f ^{( х ) d x}

-те

ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ функции /а (х, а)

Приведенная выборка обладает следующими характеристиками:

— математическое ожидание x ср = 50;

— среднеквадратическое отклонение выборочного среднего случайной величины

N

Х ^ х 2

• ⁵ = ^ NN - I ) = ^5Л7

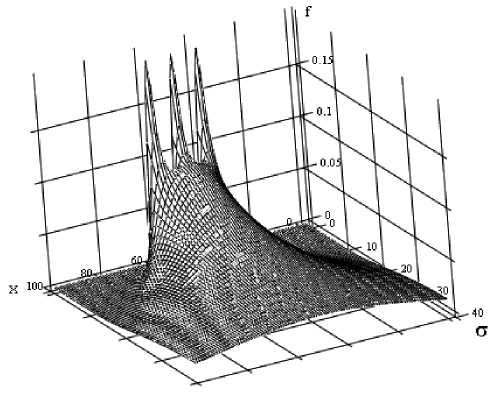
Для иллюстрации построим для этой выборки график функции / _а ( х , а ) согласно (7). На рис. 1 видно поведение функции f A при возрастании величины а . При ее малых значениях функция P ( ^х/| х _ист, а ) быстро убывает, и каждому отсчету выборки соответствует узкий пик, на который практически не оказывают влияния соседние центры распределений. С ростом а наблюдается

В качестве примера рассмотрим выборку из трех результатов измерений некоторой величины (табл. 1).

Рис. 1. График функции f_A ( x , σ ) для выборки, приведенной в табл. 1

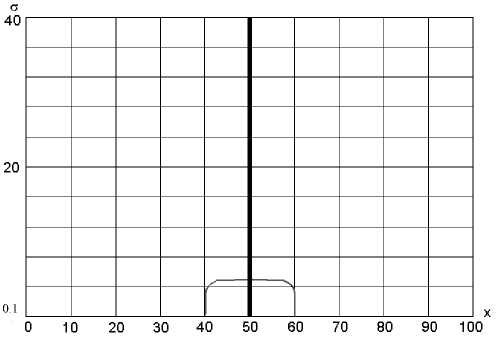
Рис. 2. Скелет максимумов функции f A ( x , σ ) для выборки, приведенной в табл. 1

ходе наличие нескольких мод при унимодальном распределении свидетельствует о необходимости увеличения дисперсии.

Таким образом, результаты анализа функции f A ( x ,у ) могут быть сопоставлены с результатами статистической обработки результатов измерений.

Покажем, что положение экстремума f A ( x ,у ) при использовании нормального распределения стремится к математическому ожиданию выборки при У ^ ^ . Действительно:

1N fA (x, У ^ N X P (xx ис1

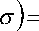
перекрытие функций распределения,

и

при

У ^ ^ f A ( x,y ) ^ о на всем интервале x . Нетрудно заметить, что при нарастании у происходит также изменение количества локальных экстремумов функции f_A ( x )| _y = _const, которое равно числу точек в выборке для у ^ 0 и единице для у ^ да. Для рассмотрения поведения локальных экстремумов функции f_A ( x )| _y = _const построим скелет максимумов f A ( x , у ) для приведенного примера.

На рис. 2 видно, что при некотором значении у наблюдается слияние линий, образованных локальными экстремумами функции f _A ( x , У ) . Точка слияния экстремумов имеет координату x = 50. Предельное значение у, при котором функция f_A ( x ) _y = _const имеет только один экстремум, для приведенной выборки равно 4.850. В сравнении с этим значением интерес представляет величина

N

X * x 2

S = । *^N ² — = 4^14, содержащая в знаменателе N ² вместо N ( N –1).

Поскольку под знаком суммы в (7) находятся плотности вероятности, функция f A ( x ,у ) также имеет физический смысл плотности вероятности. В этом случае координаты x локальных экстремумов можно рассматривать как моды анализируемой выборки при переменном значении дисперсии (или в более общем рассмотрении — масштаба вероятностного распределения). При подобном под-

N

1X

^N м У П

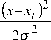
dfA(x,у) =    1 X(-2 x+2 xi) e v\u = dx    Ny 22л м   2у у

N                 ^{( x -} x i )

= -rnhr X ( xi - x ) - e ^{2 У} 2 ■             (10)

Na Aj2n i _{= 1}

⁽ x ^- x i ) 2

При У ^^ e 2 ^У ^ 1 , и с учетом того, что e ^{- x} убывает быстрее, чем возрастает любая степень x , (10) можно привести к виду

d f ( x , у ) d x

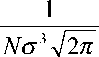
N

X ( x

= 1

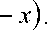
Для определения положения экстремума приравняем (11) к нулю:

1N                N з Г— X(xi - x)= 0 >X(xi - x)= 0- (12)

Ny 42л tt            i = t

Откуда получаем:

N

X, xi = Nx, или i=1

N x = N X x-          (13)

i = 1

Выражение (13) представляет собой формулу для определения среднего арифметического выборки x . Таким образом, максимум функции f A ( x , у ) при У ^^ действительно достигается для x = x _с р .

Для определения значения у , при котором наблюдается только один максимум функции

f A ( x, о ) , необходимо исследовать зависимость числа корней уравнения (10) от величины о. Так как для нормального распределения (10) является нелинейным уравнением, получение точной аналитической зависимости представляется затруднительным. Ввиду этого аналитическое определение предельного значения о представляет собой отдельную задачу.

АНАЛИЗ ПОЛУЧЕННОГО РЕШЕНИЯ

В рассмотренном выше примере была показана возможность соотнесения результатов предлагаемого метода анализа с результатами исследований известными в статистике методами. Однако существующие методы, основанные на определении математического ожидания в качестве наиболее вероятной величины и среднего квадрата отклонений (или центрального момента) для оценки степени рассеивания результатов, обладают низкой помехоустойчивостью. Действительно, при выборках небольшого объема возможно появление данных, не укладывающихся в предполагаемый закон распределения. Данная проблема иллюстрируется следующим примером (табл. 2).

Пример иллюстрирует результаты измерений некоторой физической величины с истинным значением 10. Значение этой величины было измерено 5 раз. Измерение под номером 5 представляет собой промах.

Рассмотрим влияние такого промаха на результаты статистической обработки. Математическое ожидание приведенной выборки равно 26, среднеквадратическое отклонение S = 16. Очевидно, что оценка результатов измерения на основе математического ожидания дает неверные результаты. Для сравнения построим скелет максимумов функции f_A ( x,о ) (рис. 3).

Табл. 2. Значения случайно распределенной величины

Номер измерения	Значение случайно распределенной величины
1	10
2	10
3	10
4	10
5	90

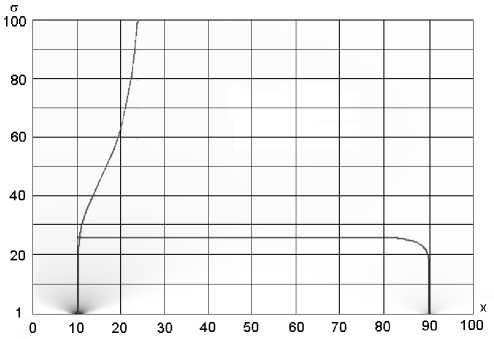
Рис. 3. Скелет максимумов функции f_A ( x , σ ) для выборки, приведенной в табл. 2

Анализ рис. 3 дает следующие характеристики выборки: координата x , при которой наблюдается единственный максимум функции f A ( x , о ) , составляет 10.323; предельное (наименьшее) значение о, при котором наблюдается единственный максимум, равно 27.235. Использование математического ожидания для оценки наиболее вероятного значения измеряемой величины привело к появлению абсолютной ошибки в 160 %, тогда как предлагаемый метод анализа в этой ситуации дал ошибку всего в 3.23 %. На рис. 3 также можно видеть, что максимум f A ( x , о ) асимптотически стремится к среднему арифметическому выборки при увеличении о. Таким образом, предлагаемый метод анализа дает возможность произвести оценку по среднему арифметическому, но вместе с тем имеется возможность получения альтернативных результатов, которые в некоторых случаях дают более точное представление об измеряемой величине. Необходимо отметить, что методика получения величины математического ожидания является частным случаем предлагаемого подхода (для о ^ ^ ).

Приведенный пример иллюстрирует важнейшее свойство предлагаемого метода анализа — малые отклонения результирующей моды при существенных выбросах в исходной выборке. Вместе с тем при анализе не используются явные методы фильтрации или отбрасывания данных, по каким-либо параметрам кажущихся недостоверными. И при этом имеется принципиальное отличие от метода оценки по моде распределения, поскольку для определения моды требуется предварительно получить закон распределения конкретной выборки, тогда как в формулировке поставленной задачи предполагается, что апостериорные

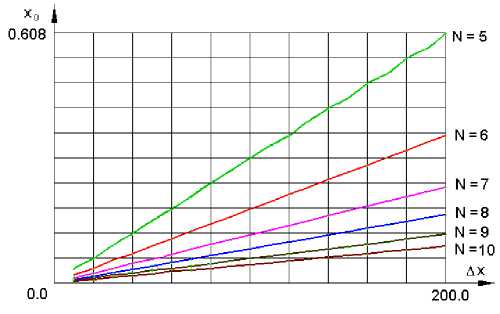
Рис. 4. Зависимость величины отклонения моды x0 от амплитуды промаха для различных объемов анализируемой выборки

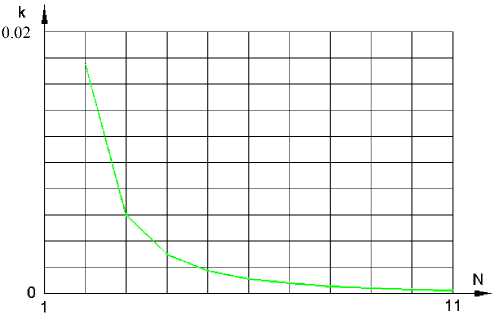
Рис. 5. Зависимость коэффициента наклона k от объема выборки N при наличии в ней одного промаха.

вероятности тех или иных событий неизвестны. В рассматриваемой же методике для проведения анализа оказывается достаточным наличие априорной информации о предполагаемом законе распределения.

Влияние амплитуды промаха на степень отклонения моды иллюстрируется рис. 4. Здесь представлены результаты анализа выборки из N значений, одно из которых отличается от остальных на величину Δ x . В процессе анализа определяется мода x 0 .

Из рассмотрения рис. 4 видно, что зависимость x0(Δx) достаточно хорошо аппроксимируется линейной функцией. Коэффициент наклона этой функции резко уменьшается при увеличении объема выборки. Зависимость коэффициента наклона k от объема выборки N при наличии в ней одного промаха приведена на рис. 5.

На рис. 5 видно, что влияние амплитуды промаха на отклонение моды резко падает уже при объеме выборки 4–5. Такое количество измерений можно обеспечить в большинстве измерительных приборов. Можно заметить, что наличие одного промаха на 4–5 измерений соответствует измерительному средству, дающему достоверные результаты в 75–80 % случаев, что, вообще говоря, является низким показателем. Таким образом, обработка результатов измерений по предлагаемой методике может использоваться в том числе и в измерительных приборах, подверженных частым возмущающим воздействиям, приводящим к появлению промахов. Это свойство, наряду с небольшим объемом выборки, необходимым для оценки измеряемой величины, позволяет существенно улучшить эксплуатационные характеристики измерительных приборов, использующих данную методику оценки.

ВЫВОДЫ

• 1.    Предложенный метод оценки результатов многократных измерений основан на использовании теоремы Бейеса и предполагает рассмотрение отсчетов анализируемой выборки в качестве центров распределения некоторых априорных функций распределения вероятности. Ключевым понятием метода является функция плотности вероятности с аргументами "измеряемая величина" и "масштаб априорной функции распределения вероятности". Оценка результатов многократных измерений производится исходя из анализа полученной функции.

• 2.    Из анализа функции плотности вероятности могут быть получены как математическое ожидание, так и моды случайно распределенной величины, определенные для различных масштабов априорной функции распределения вероятности. Особенный интерес представляет мода, полученная для масштаба, при котором наблюдается единственный экстремум функции распределения вероятности в зависимости от значения измеряемой величины. Это значение обладает весьма высокой устойчивостью к наличию промахов в исходных данных и вместе с тем обеспечивает точную оценку результатов при малом объеме выборки.

• 3.    Несмотря на то что в рассмотренных в статье примерах используется гауссовское распределение, не существует ограничений на выбор априорной функции распределения вероятности. Это делает метод универсальным и пригодным для широкого класса задач статистической обработки.

• 4.    Необходимость определения числа экстремумов затрудняет аналитическое нахождение

масштаба априорной функции распределения вероятности, при котором наблюдается единственная мода. Это обусловливает ориентацию на численный анализ с использованием ЭВМ. Вместе с тем относительная простота метода делает удобной его алгоритмизацию и позволяет использовать для автоматизации измерительных процессов.