Оценка шероховатости лопаток газотурбинных двигателей с заданной вероятностью на основе компьютерной обработки видеоизображений их поверхностей

дрической поверхности ролика подшипника. При этом оценка шероховатости выполнялась на основе измерения среднего периода колебания автокорреляционных функций, полученных по видеоизображениям исследуемых поверхностей.

В предлагаемой работе использовался тот же самый оптико-электронный комплекс, но с новой методикой, позволяющей определять шероховатость поверхности с заданной вероятностью распознавания на основе вычисления средней амплитуды переменной составляющей автокорреляционной функции. Схема исследовательского комплекса, приведёна на рис.1. Для исследования были изготовлены 2 образца (образец № 1 и образец № 2) из жаропрочного сплава на никелевой основе ЖС6ФИ. Финишная обработка этих образцов производилась методом бесцентрового шлифования на станке СВА АКМ 25/1. Кроме того, для исследования в качестве эталонов были взяты: полированная поверхность (образец № 3) и поверхность зеркала (образец № 4). Полирование производилось на виброконтакт-ном станке ЛВП4.

Для этих же образцов на профилографе модели SJ - 201P были записаны профилограммы и определены стандартные параметры шероховатости: образец № 1 имел Ra = 0,13 мкм , образец № 2 — Ra = 0,084 мкм образец № 3 - Ra = 0,048 мкм , образец № 4- Ra = 0,022 мкм . Найденные значения среднего арифметического отклонения профиля представляют собой средние значения, вычисленные по 10 измерениям для каждого образца. Видеоизображения поверхностей исследуемых образцов приведены на рис. 2.

Как видно из приведенных рисунков, выбранные образцы для исследования существенно отличаются друг от друга по внешнему виду. Так, например, для образцов после шлифования наблюдается ориентированная в вертикальном на-

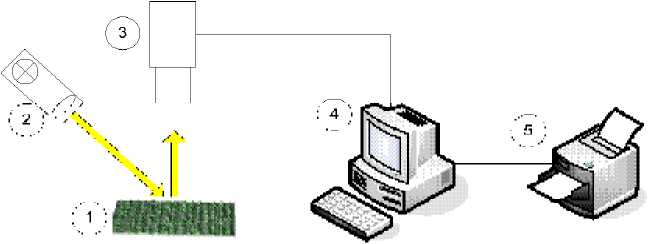
Рис. 1. Схема исследовательского комплекса:

1 – исследуемая поверхность;

2 – источник параллельного светового потока; 3 – видеокамера;4 – компьютер; 5 – принтер

образец №1 образец №2        образец №3       образец №4

Рис. 2. Видеоизображения исследуемых поверхностей

правлении текстура в виде чередования черных и белых полос. Для поверхности образца № 3 после полирования ориентированная в вертикальном направлении текстура вообще отсутствует. В ней наблюдаются на черном фоне отдельные белые фрагменты различного размера, расположенные случайным образом по поверхности. Изображение поверхности зеркала практически представляет из себя сплошное чёрное поле с очень редкими вкраплениями белых точек.

Для определения признаков, по которым с заданной вероятностью можно определить шероховатость поверхности была разработана следующая методика. Вначале исходное черно-белое изображение размером 320х240 пикселей преобразовывалось в формат 1пиксель-1байт. Таким образом, диапазон изменения сигнала яркости по строке видеокадра составил 0-255 условных единиц. Характерные изменения уровня яркости видеосигналов по строке видеокадра для поверхностей исследуемых образцов приведены на рис. 3. Анализ приведенных видеосигналов показывает влияние шероховатости поверхности как на амплитуду видеосигнала, так и на его спектр. При этом наблюдается уменьшение амплитуды сигнала с уменьшением шероховатости, особенно при переходе от шлифованной поверхности к полированной.

На следующем этапе многоградационное по яркости черно-белое изображение преобразовывалось в бинарное. Преобразование осуществлялось на основе медианной фильтрации окном с размерами 21 х21 пиксель [3]. В результате та- кого преобразования получались бинарные изображения формата 299 х 219 пикселей, приведенные на рис. 4.

Анализ полученных бинарных изображений также показывает влияние шероховатости поверхности на её текстуру. Так, например, для образца № 1 с более грубой шероховатостью наблюдается более четкая ориентация черных и белых компонент (полос) в вертикальном направлении, чем для образца № 2 с наименьшей шероховатостью после шлифования. Для поверхности образца после полирования и поверхности зеркала (образцы № 3 и № 4) текстура носит более случайный характер. В ней наблюдаются на черном фоне отдельные белые фрагменты различного размера, расположенные случайным образом по поверхности. Отмеченная особенность говорит о возрастающем влиянии случайной составляющей в формировании текстуры поверхности с наименьшими показателями по Ra.

В дальнейшем, бинарные изображения преобразовывались по методике, изложенной в работе [2]. В бинарном изображении исследуемой поверхности, начиная с первой верхней строки, выделялась полоса шириной в N пикселей. По центру этой полосы задавался эталон размером N _х N пикселя. Этот эталон перемещался по всей выделенной полосе с шагом в 1 пиксель. При каждом совмещении эталона с текущим фрагментом бинарного изображения подсчитывалась сумма совпавших пикселей в эталоне и текущем фрагменте. Этой сумме придавалось смысловое значение коэффициента корреляции.

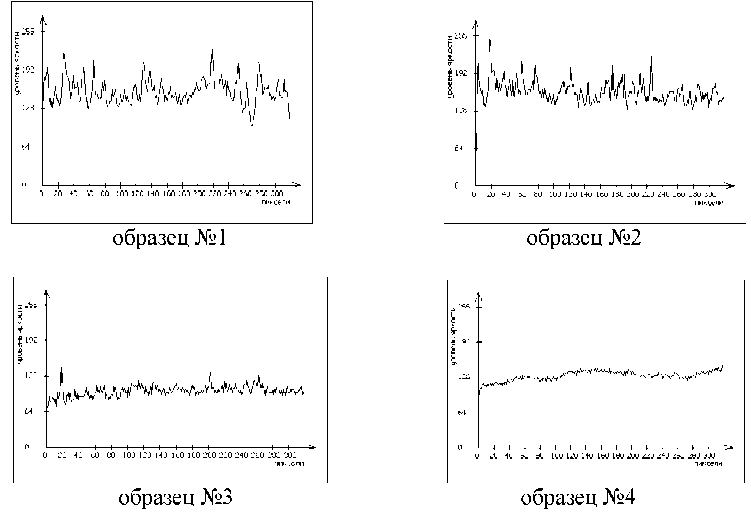
Рис. 3. Уровень яркости видеосигналов для исследуемых поверхностей образцов.

Рис. 4. Бинарные изображения исследуемых поверхностей.

Для получения нормированного коэффициента корреляции найденная сумма делилась на N _х N пикселя. Таким образом, при полном совпадении эталона и текущего фрагмента изображения, коэффициент корреляции принимал значение равное 1, которому в памяти компьютера сопоставлялся байт со значением 0 FFH . Нулевому значению коэффициента корреляции при полном несовпадении эталона и текущего фрагмента соответствовал байт со значением 00 H . После подсчета автокорреляционной функции в выделенной полосе задавалась следующая полоса того же формата, но смещенная вниз по вертикали на один пиксель и в ней производились те же самые вычисления, что и в первой полосе. Общее количество таких полос в кадре 299 х 219 пикселей было 219- N , а количество найденных коэффициентов корреляции в полосе составило 299– N значений. Таким образом, после обработки всего бинарного кадра для исследуемых образцов получались многоградационные автокорреляционные поверхности, характерный вид которых при размере эталона 16 х 16 пикселя приведен на рис. 5.

Их анализ показывает, что в этом случае также наблюдается ориентированная в вертикальном направлении текстура, при этом ориентация более четко выражена для поверхности с более грубой шероховатостью (образец № 1). Характерные изменения нормированных корреляционных сигналов приведены на рис. 6.

Из приведенных зависимостей также видно, что для поверхности с наилучшей шероховатостью (образцы № 3 и №4) наблюдается резкое падение амплитуды корреляционного сигнала от места взятия эталона, что может служить характерным признаком для идентификации (распознавания) изделий с заданными высокими показателями по качеству поверхности. Таким образом, поверхности с различной шероховатостью имеют и существенно различные двухмерные автокорреляционные функции, полученные в результате обработки бинарных изображений этих поверхностей.

Для введения количественной оценки, на основании которой можно с заданной вероятностью надёжно распознать неизвестную шероховатость исследуемой поверхности, в отличии от

Рис. 5. Нормированные автокорреляционные поверхности исследуемых образцов.

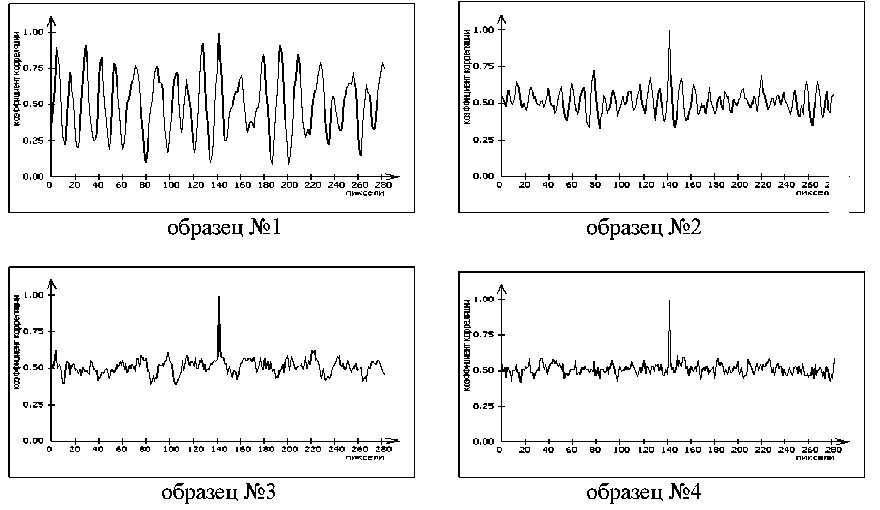
Рис. 6. Графики изменения нормированных корреляционных сигналов исследуемых поверхностей

методики, изложенной в работе [2], был применен следующий алгоритм. В автокорреляционной поверхности задавался порог B_п , которому соответствовал коэффициент корреляции r = 0,5 . Затем из каждого байта этой поверхности B_i вычиталось значение B_п , и подсчитывалась сумма всех разностей по абсолютной величине. Затем эта сумма делилась на площадь автокорреляционной поверхности:

U =

S

Е I B - ® .\

I =1 __________________

S

где S = N х N - количество пикселей (байт) в анализируемой поверхности.

Полученной таким образом оценке U можно придать смысловое значение средней амплитуды переменной составляющей двухмерной автокорреляционной функции. Отметим, что величина U также является безразмерной величиной, как и Bi . Применив рассмотренный алгоритм получения оценки шероховатости к исследуемым поверхностям для различных размеров эталонов были получены результаты, приведенные в табл. 1. Анализ приведенных данных показывает существенное влияние размера эта- лона как на среднюю амплитуду переменной составляющей автокорреляционной функции (АКФ), так и на её среднеквадратическое отклонение (СКО). Наилучшее различие по амплитуде и СКО для образцов с различной шероховатостью наблюдается при использовании эталонов размером 2 х 2 , 4 х 4 , 8 х 8 и 16 х 16 пикселя При этом для эталона 4 х 4 пикселя наблюдается более равномерное различие в U для образцов с различной шероховатостью.

Для этого эталона на рис. 7 приведен график зависимости среднего арифметического отклонения профиля исследуемых поверхностей от средней амплитуды переменной составляющей АКФ.

Как видно из приведенного графика, рассматриваемая зависимость имеет линейный характер. С увеличением среднего арифметического отклонения профиля от средней линии возрастает и средняя амплитуда переменной составляющей в автокорреляционной функции. Аналитическая зависимость Ra = f ( U ) для данного случая может быть представлена в виде уравнения:

Ra =(4,5 * U - 114)* 10 ^-3, мкм (2)

Для определения доверительных интервалов I_b, в которые попадает случайная величина U , зададим вероятность распознавания шерохова-

Таблица 1. Зависимость средней амплитуды переменной составляющей автокорреляционной функции от размера эталона

Ra, мкм	Средняя амплитуда U
	эталон 2x2	эталон 4x4	эталон 8x8	эталон 16x16	эталон 32x32	эталон 64x64
0,022	□ EMBED	U = 30,2 <7 = 1,7	(7 = 16,0 <7 = 1,5	U = 8,7 <7 = 1,2	U = 5,3 <т = 0,9	U = 3,7 <т = 0,8
0,048	и = 60,7 <7 = 2,8	и = 36,1 <7 = 1,9	U = 20,2 <7 = 1,8	(7 = 11,3 <7 = 1,6	(7 = 7,4 <7 = 1,4	(7 = 5,6 <7 = 1,2
0,084	U = 70,8 <7 = 3,6	U = 44,8 о-= 2,1	U = 26,9 о- = 1,42	(7 = 15,9 о-= 1,2	(7 = 9,6 ст = 1,1	(7 = 11,4 о-= 2,7
0,13	и = 76,2 <7 = 8,4	U = 54,3 <7 = 5,6	U = 37,1 <7 = 4,8	U = 24,2 <7 = 3,7	(7 = 16,3 <7 = 3,5	(7 = 17,2 <7 = 2,7

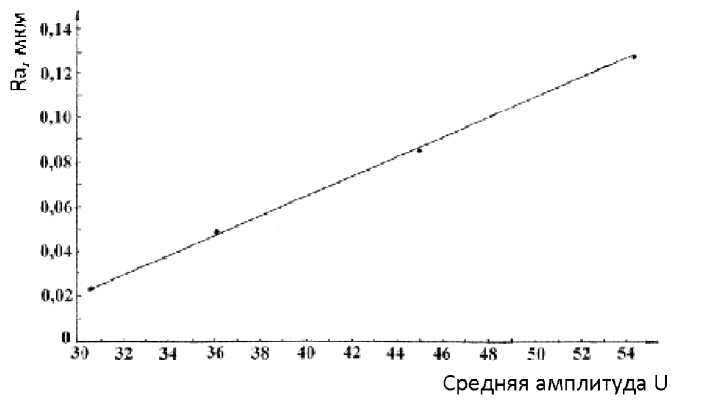
Рис. 7. Зависимость Ra , мкм = f (U )

тости поверхности равной Р=0,99. Проведенными исследованиями также было установлено, что образец № 1 имел среднеквадратическое отклонение от U , равное с т = 5,6 , образец № 2 - с т = 2,1, образец № 3 - с = 1,9 , и образец №4 - с = 1,7, а сама случайная величина U подчиняется нормальному закону распределения. В этом случае число среднеквадратических отклонений t_b, которое нужно отложить вправо и влево от центра рассеивания для того, чтобы вероятность попадания случайной величины U в полученный интервал была P = 0,99 , имеет значение 2,576 [5]. Для каждого образца было обработано по 30 изображений с различных участков исследуемой поверхности, т.е. n=30. Тогда среднеквадратическое отклонение оценки для U определяется по формуле [5]:

σср

σ Т ⁼     .                 (3)

n

Следовательно, для образца № 1 имеем C T = 1,0, для образца № 2 - c T = 0,4 , для образца № 3 - а _т = 0,3 , и для образца №4 - с _т = 0,3.

Через величины tb и с _т доверительный интервал выражается в виде:

I в = (^{U -} t _P * с ; U + b * с ).    (4)

Округляя вычисленные значения t р * cT в сторону увеличения, получим:

для образца № 1 - I р = 2,6 , 51,7 <  U <  56,9; для образца № 2 - I _р = 1,0, 43,8 <  U <  45,8; для образца № 3 - I _р = 0,8, 35,3 <  U <  36,9; для образца № 4 - I р = 0,8, 29,4 <  U <  31,0;

Как видно из приведенных данных, довери- тельные интервалы для U с увеличением шеро- ховатости возрастают и, что очень важно, не перекрываются. График зависимости Iр = f (U)

приведен на рис. 8.

Как видно из приведенного графика, зависи мость I , = f ( U ) для нашего случая имеет не

-

-

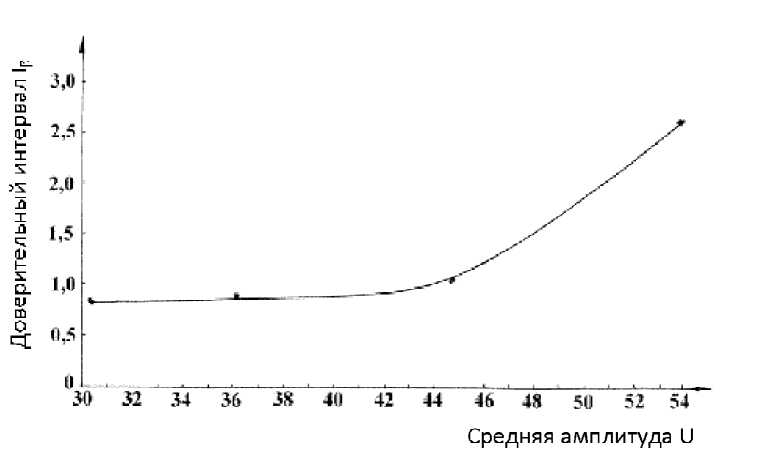
Рис. 8. Зависимость доверительного интервала от средней амплитуды переменной составляющей автокорреляционной функции

линейный характер. Следовательно, для неё можно найти аналитическое выражение, используя интерполяционную формулу Лагранжа [4]. Проведя необходимые вычисления, получим:

I _e = ( 3 * U ³ - 318 * U ² + 11156 * U - 121500 ) * 10 ^{- 4} .(5)

Таким образом, определяя с использованием оптико-электронного комплекса и рассмотренной выше методики среднюю амплитуду колебания переменной составляющей автокорреляционной функции U можно с использованием аналитических зависимостей (2), (4) и (5) вычислять среднее арифметическое отклонение профиля исследуемой поверхности, а также диапазон изменений Ra с заданной вероятностью распознавания.

Рассмотренная методика была применена к оценке шероховатости поверхности профиля пера лопатки 1-ой ступени ГТД, вид которой приведён на рис. 9.

Предварительно профиль лопатки шлифовался накатными абразивными кругами на полиро-

Рис. 9. Лопатка 1-ой ступени турбины авиационного двигателя вальных бабках. Лопатка 1-ой ступени турбины изготовлена из жаропрочного сплава на никелевой основе ЖС6ФИ. Обработка производилась абразивными зернами из электрокорунда белого (24А), с режимами: скорость круга 45 м/с, ручная врезная подача. Полирование производилось на виб-роконтактном станке ЛВП4 абразивными шкурками на бумажной основе зернами 24А, зернистостью 5, то есть также как и исследуемые образцы.

Для анализа были взяты участки поверхности лопатки после операции полирования, а для получения автокорреляционной поверхности использовался эталон размером 4 x 4 . На рис. 10 приведены: бинарное изображение, автокорреляционная поверхность и изменение коэффициента корреляции для одного из выбранных участков.

Обработка результатов эксперимента показала, что после операции полирования U = 42,1. Подставляя это значение в формулу (5), находим I р = 0,8 . Следовательно, U min = 41,3 и U max = 42,9 . Используя формулу (2) определяем, что Ra = 0,075 мкм , Ra min = 0,072 мкм , Ra max = 0,079 мкм , что вполне согласуется с техническими условиями, предъявляемыми к шероховатостям отмеченных изделий. Аналогичные данные получены и на других участках поверхности лопатки, которые укладываются в данные пределы.

Расхождение найденных значений с результатами измерения Ra непосредственно по профилограммам составило около 5%. Это незначительное расхождение можно объяснить тем, что профилограммы дают ограниченную информацию о рельефе всей поверхности, тогда как оптико-электронный комплекс позволяет обрабатывать двухмерные изображения

Рис. 10. а – бинарное изображение; б – автокорреляционная поверхность;

в – изменение коэффициент автокорреляции для одного из выбранных участков поверхности лопатки

Таким образом, рассмотренный оптико-электронный комплекс и методика определения стандартных параметров шероховатости на основе компьютерной обработки видеоизображений анализируемых участков позволяют оценивать качество поверхности различных изделий, не нанося ей механических повреждений и в тех местах, где применение других методов не представляется возможным. Кроме того, этот комплекс позволяет организовать оперативный, 100% контроль качества выпускаемых изделий непосредственно в ходе их производства.