Оценка силы трения плунжера о цилиндр штангового скважинного насоса при проектировании колонны штанг

трения в УСШН при ходе вверх G_mp = 2500l , [Н], где l – длина хода полированного штока, м [2].

Сила трения штанг о насосно-компрессорные трубы для обычных условий составляет около 2% от веса штанг. При добыче вязких нефтей (более 0,03 Па·с) она увеличивается и может превышать 1кН. Сила трения в паре плунжер – цилиндр гораздо больше, и может достигать 3 кН [1]. Она зависит от диаметра насоса, вязкости добываемой нефти, группы посадки плунжера, количества механических примесей.

Определением сил трения в плунжерной паре штанговых скважинных насосов, занимались многие авторы [1, 2, 3, 4, 5, 6].

В работе [6] представлена зависимость силы трения Fтр от диаметра насоса D:

F_тр = 25000D ,               (1)

Согласно (1), значение силы трения плунжера о цилиндр для плунжера, диаметром 43 мм равно 1075 Н.

Для искривленных скважин, в которых возможен изгиб штангового насоса, была установлена уточненная зависимость учитывающая радиус кривизны участка скважины R [6]:

, ME

F_mp = 25000 - D + 7,2 - 10 ^-3 -^= , (2) где ∆J – разность моментов инерции сечения плунжера и цилиндра, м⁴;

E – модуль Юнга, Па ;

δ – зазор между плунжером и цилиндром, м.

При том же плунжере диаметром 43 мм, R =100 м, δ = 0,1 мм; второе слагаемое в уравнении (2) составляет 320 Н, а сила F_тр = 2070 Н.

Зависимости (3) и (4), учитывающие диаметр насоса и величину зазора в плунжерной паре, предложены В.И Сердюком на основе экспериментальных исследований [1].

При смазке плунжерной пары водой:

Fmp = 1,84 D - 137 ,           (3)

При смазке плунжерной пары трансформаторным маслом:

F ™, = 1’65 D - ¹²⁷ ,            (4)

δ

— dP ( r ² - R 2) + 4 • ц dz ^ЦЛ

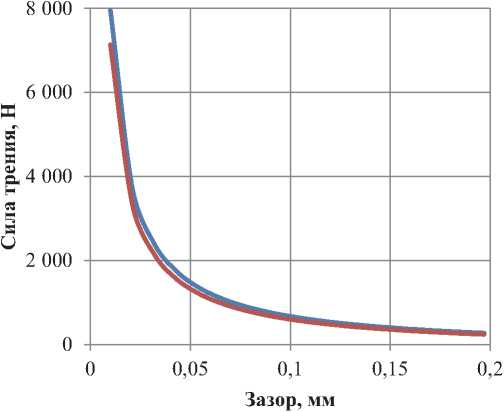
Для насоса с диаметром плунжера равным 43 мм, построен график по зависимостям 3 и 4 (рис. 1)

Из рис. 1 видно, что при зазоре менее 0,25 мм, что соответствует нулевой посадке плунжера в цилиндре, силы трения достигают значений более 3 кН.

Величины сил трения расчитанных по различным зависимостям значительны, и их необ-

ln(—)

+ (+v +    dP(R² -r²)) —^IP-

^V .Л                      ЦЛ .Л                   ,

4 • Ц dz ⁴        i_n, ^г „л )

R цл

ходимо учитывать при проектировании штанговых колонн [12].

Для полноценного анализа силы трения возникающей в плунжерной паре, необходимо также рассмотреть гидродинамическое трение при течении жидкости в зазоре плунжерной пары.

Влияние гидродинамического трения при течении жидкости в зазоре плунжерной пары

можно определить, рассмотрев вертикально расположенный насос, в котором плунжер и ци-

линдр расположены концентрично.

Для вязких жидкостей зависимость касательных напряжений от скорости движения плунжера определяться по закону Ньютона

где    – перепад давления жидкости на едини- dz цу длины, Па/м;

r – расстояние от оси симметрии цилиндра до его стенки, м.

R_цл – внутренний радиус цилиндра, м;

r_пл – наружный радиус плунжера, м;

v_пл – скорость движения плунжера, м/с.

Решая уравнение (6) при известных радиусах цилиндра и плунжера, получим зависимость возникающих касательных напряжений на поверхности плунжера при ходе вверх и вниз от скорости плунжера, перепада давления и вязкости жидкости:

Г P P • ( R ² - r²) ЦЛ .Л

T =-- .^Л  -            + V

τ =- µ

dV z dr ^,

где μ – динамическая вязкость жидкости, Па ^. с;

V_z – скорость движения слоя жидкости, м/с;

r – расстояние от оси симметрии цилиндра до его стенки, м.

Скорость движения слоя жидкости в кольцевом пространстве определяется зависимостью [7]:

r

4 • r • ln( "^Л ) ^ЦЛ

μ

.Л---^r— , (7)

r • ln(- . ^)

^ЦЛ

где Р – перепад давления жидкости на плунжере.

Для плунжера c площадью поверхности S, сила трения будет определяться зависимостью:

r P F™, = ^ ( r^

P - ( R ² - r²) ЦЛ ПЛ

r

4 • r • ln( -^)

ИЛ

Rm

- ----Ц. ) ^, (8)

r ™ • ^ln^{(    )}

R- ЦЛ

Вода

Масло трансформаторное

Рис. 1. Зависимость силы трения при различных смазках от величины зазора между плунжером и цилиндром при диаметре плунжера 43 мм

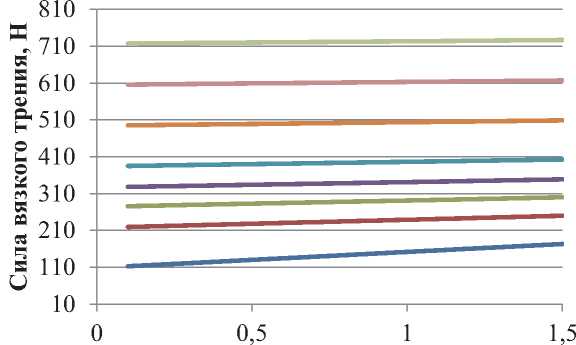
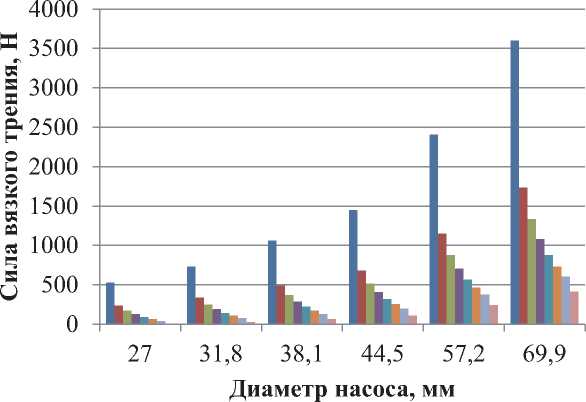
По формуле (8) построены графики зависимости силы вязкого трения при движении плунжера диаметром 43 мм и длиной 1,6м от его скорости при различных величинах зазора (рис. 2) и зависимость силы вязкого трения от диаметра насоса (рис. 3). Расчеты проводились для жидкости вязкостью 0,01 мПа ^. с (рис. 2) и 0,1 мПа ^. с (рис. 3), при давлении 20 МПа.

Наибольшая интенсивность увеличения сил вязкого трения при увеличении скорости плунжера, наблюдаются при малых величинах зазора (рис. 2).

При максимальных значениях вязкости жидкости откачиваемой штанговыми насосами (0,1 мПа ^. с), значения сил вязкого трения сопоставимы с силами трения металл по металлу (рис. 3). При этом видно, что с увеличением зазора плунжерной пары, сила вязкого трения уменьшается.

При нагрузке на головку балансира 100 кН силы трения, доля которых составляет 2–5%, равны 2–5 кН (200 – 500 кгс). При относительно небольшой нагрузке при подборе колонны штанг необходимо учитывать, что направление действия сил трения меняется на противоположное два раза за цикл качаний головки балансира и в расчетах учитывается как составляющая амплитудного значения асимметричного цикла. С увеличением глубины скважины именно из-за сил трения в паре плунжер-цилиндр в асимметричном цикле появляются отрицательные значения, причем ассиметрия цикла может изменяться даже при изменении состава добываемой нефти и механических примесей, а так же из-за известной неравномерности движения плунжера под действием инерционных и вибрационных нагрузок. При большой силе трения в паре плунжер – цилиндр может возникнуть зависание колонны штанг при ходе вниз, что требует применения специальных мер, например утяжеленного низа. Согласно статистике при

Скорость плунжера, м/с

Зазор

^—0.025 мм 0.05 мм

^-0.063 мм

^—0.075 мм

---0.088 мм

^—0.113 мм

^—0.1 мм

^—0.138 мм 0.163 мм

Рис. 2. Зависимость силы вязкого трения в плунжерной от скорости плунжера

• ■    №^РММ

• ■    0,05 мм

0,063 мм

• ■    0,075 мм

• ■    0,088 мм

0,1 мм

• ■    0,113 мм

• ■    0,138 мм

Рис. 3. Зависимость силы вязкого трения в плунжерной паре от диаметра насоса

увеличении диаметра штанговых насосов и диаметра насосных штанг аварии штанговой колонны происходят в нижней ее части из-за появления знакопеременных нагрузок, обусловленных в том числе и силами трения в плунжерной паре при ходе вниз.

Длительная работа штанговых насосов ведет к большому количеству циклов переменных, а в нижней части колонны и знакопеременных нагрузок. Пределом усталости для металлов является наибольшее напряжение, которое выдерживает образец при 10 млн. циклов симметричной нагрузки. В процессе работы ШСН такое число циклов возникает при 10 ходах в минуту за 700 сут.

Для приведенных напряжений в колонне штанг известны формулы:

° „р = V ° макс '° а формула И.А. Одинга; (9)

° „_р = ° _а + 0,2 ° _ср формула М.П. Марковца; (10) ° „р = ° макс - 0,56 ° мак фоРмУла Б.Б. КРУмана. ⁽¹¹⁾

Значения σ _пр вычисленные по этим формулам отличаются не более, чем на 5 – 10 %.

Также известен метод вычисления предельного приведенного напряжения по А.С. Вир-новскому для насосной штанги стандартной конструкции, на основе модифицированной диаграммы Гудмана [8].

Сила трения равная 4 кН, вызовет в штангах диаметром 16 мм амплитудное напряжение равное 20 МПа. Приведенное напряжение например, для стали 20Н2М при нормализации равно 60 – 90 МПа. Как видно, примерно треть от допускаемой нагрузки создается только силами трения, в то время как аналогичные статические нагрузки, согласно формуле М.П. Марковца вызовут приведенные напряжения в пять раз меньшие, равные 4 МПа. По этой причине для увеличения долговечности штанговой колонны необходимо в первую очередь учитывать знакопеременные нагрузки – силы трения, инерционные и вибрационные нагрузки/

Формула М.П. Марковца наглядно показывает долю σ _a при расчете приведенного напряжения – она в пять раз больше, чем влияние σ _ср.

Из теории усталостной прочности известна более точная формула определения приведенных напряжений, чем формула М.П. Марковца [9]

°„р =°а -k|- + V°°ср , (12) р е°в° р где kσ – эффективный коэффициент концентрации напряжений;

ε_σ – масштабный коэффициент;

β_σ – коэффициент состояния поверхности, зависящий от шероховатости поверхности и механических свойств поверхностного слоя, наличия коррозионных повреждений, упрочняющей поверхностной обработки;

ψ_σ – коэффициент влияния постоянных нормальных напряжений.

Для определения запасов усталостной прочности следует учесть возможный характер изменения переменных и постоянных напряжений [9].

Зависимость предельного значения амплитуды переменных напряжений (предела выносливости по амплитуде при асимметричном цикле) σ _a от среднего (статического) напряжения σ _ср, σ _a = f( σ _ср) имеет вид, представленный на рис. 4 [10].

Для упрощения расчетов используют линейную зависимость, например формулу М.П. Марковца.

Количество циклов до разрушения является случайной величиной поскольку практика показывает, что колонна может работать надежно с превышением допустимого напряжения, либо, наоборот, число обрывов может увеличиться при более низких напряжениях.

Выше рассмотрено трение при наличии смазки. В случае сухого трения, например, при спуске или подъеме насоса или при его запуске, при трении штанг о НКТ, плунжера о цилиндр, колебания силы трения могут привести к релаксационным колебаниям, которые при определенном энергетическом балансе приводят к незатухающим автоколебательным процессам [4], что отрицательно сказывается на долговечности штанг.

Релаксационные колебания по сравнению с обычными колебаниями сил трения имеют

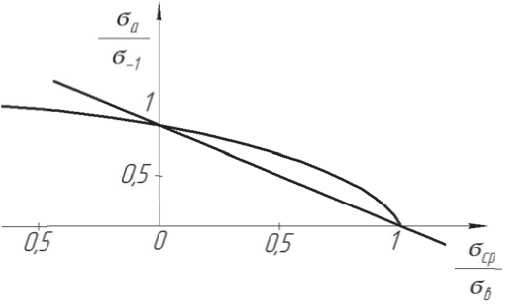
Рис. 4. Влияние статического напряжения на предел выносливости (кривая предельных амплитуд)

амплитуду в три - четыре раза меньше. Но их частота гораздо выше. По расчетам один цикл релаксационных колебаний происходит за полторы-две секунды, вследствие чего 10 млн. циклов достигается за гораздо меньший проме- жуток времени.

Колонна штанг, является упругой системой. Ограниченная жесткость штанг за счет упругих деформаций, приводит к рассогласованию движения устьевого штока и плунжера. Рассогласование возможно как по скорости, так и по перемещению. Способствует рассогласованию повышенная вязкость нефти.

Релаксационные колебания вызываются нестабильностью сил трения при контактном взаимодействии перемещающихся тел, разницей сил трения покоя и скольжения. При малых скоростях перемещения наблюдается прерывистое движение в виде «остановки» и «скачка».

Коэффициент прерывистости движения при релаксационных колебаниях

V =

R i - R 2 mpv

где R ₁ – сила трения покоя, Н;

R 2 - сила трения скольжения, R 1 >  R 2 , Н;

m – масса плунжера, кг;

• p – частота собственных колебаний колонны штанг; p ² = c / m , 1/с;

• c – жесткость колонны штанг, Н/м;

• v – скорость перемещения головки балансира, м/с.

Релаксационные колебания характеризуются следующими основными параметрами: временем от момента срыва до новой остановки (продолжительностью скачка) T1 , временем остановки T2 , периодом колебаний T , максимальной скоростью при скачке Vmax, и другими.

_ 2 z

Tx = -(л-arctg y),(14)

p

72 = —,(15)

p

_ _ _ 2 ,

T = T + T2 = —(п + y-arctg y),(16)

p

Релаксационные колебания возможны лишь при скоростях ниже критических.

В теории фрикционных колебаний введено понятие критической скорости. Если известны свойства упругой системы (жесткость, масса, трение, коэффициент затухания), то критическое значение скорости v_c приближенно имеет вид

R . - R 2

vc

V4П0 cm ’

где 9 - коэффициент затухания.

Коэффициент затухания 9 изменяется в пределах 0,012-0,160 [11].

При скорости перемещения устьевого штока больше критического значения, движение штанговой колонны и плунжера происходит непрерывно, а при скоростях меньших критического значения неизбежно их скачкообразное перемещение.

Принимая глубину подвески насоса 1000 м, R 1 = 4 кН, R 2 = 0,75 R 1 , 9 = 0,012 согласно (17) получаем значения критических скоростей для штанг диаметром 16 мм, 19 мм, 22 мм, 25 мм, 28 мм. Они соответственно равны 0,32 м/с, 0,22 м/с, 0,17 м/с, 0,13 м/с, 0,10 м/с. Полученные значения скоростей входят в рабочий диапазон современных станков-качалок.

Период релаксационных колебаний для штанг диаметром 16 мм и длиной штанговой колонны 1000 м, рассчитанный, по формуле (4) при скоростях устьевого штока менее 0,32 м/с равен 1,5 с. Десять миллионов циклов при амплитуде 1 кН достигается за 77 суток.

В современных условиях в связи с стремлением обеспечить непрерывные режимы откачки при эксплуатации малодебитных скважин, часто используется тихоходный режим работы станка-качалки [13]. При таких режимах возможно возникновение релаксационных колебаний, которые в виду их большой частоты, могут оказаться опасными и потребуют дополнительных мер для их предупреждения.

ВЫВОДЫ

При подборе ШСНУ необходимо учитывать влияние амплитудных напряжений от сил трения в плунжерной паре даже при статическом режиме работы ШСНУ. Наиболее неблагоприятные условия – возникновение сухого трения. При сухом трении колебания силы трения могут перейти в релаксационные колебания и привести к автоколебательным процессам, что вызовет увеличение циклов знакопеременных напряжений и снизит долговечность штанговой колонны.