Оценка сложности систем

Введение. Все объекты окружающего нас мира являются системными, т. е. могут быть представлены в виде различных систем. Это относится и к искусственно созданным человеком техническим объектам. Целью создания любой технической системы является результат ее функционирования, а эффективностью - степень соответствия этого результата поставленной цели. При разработке системных объектов техносферы часто возникает задача выбора лучшей системы из нескольких при равной эффективности. Сложность систем при одинаковых функциях определяет целый комплекс экономических и эксплуатационных качеств. В этих условиях интуитивный выбор не может быть рациональным. Кроме того, объективная оценка сложности позволит классифицировать системы по более общим признакам, не связанным с конкретной областью их применения. Таким образом, возникает вопрос о критерии объективной количественной оценки сложности технических систем как их основного структурного параметра.

Состояние вопроса. В литературе [1, 2] часто встречаются термины «большая» или «сложная» система. Но большое число элементов не обязательно делает систему сложной (например, цепная система с одной связью между элементами). Иногда считается, что сложность системы определяется важностью выполняемых ею функций. Действительно, функция искусственного сердечного клапана очень важна, но это не влияет на его сложность. Иногда сложной называется система, модель которой не адекватна поставленной цели [2], а некоторые авторы большой считают систему, которую наблюдатель может рассматривать только по частям [3]. Согласиться с подобными определениями нельзя.

Сложность систем рекомендуется оценивать степенью влияния случайных факторов, числом непересекающихся системных функций и, наконец, системными параметрами: количеством элементов, числом связей и иерархических уровней. Последние рекомендации [4] как количественные представляются наиболее приемлемыми, но методика их использования не разработана.

Принято считать, что никакой четкой границы, отделяющей простые системы от сложных, не может существовать [1]. При этом авторы предлагают оценивать сложность систем субъективно, используя однотипные элементы реальных систем (Л), некоторые числа (5) и вспомогательную величину (а), a=M/N(N-l) ,                                       (1)

где м— фактическое число связей в реальной системе.

Тогда сложность системы оценивается количественной величиной р

8 = (иуо)^8^ ,                          (2)

г=1

где v - коэффициент, учитывающий сложность связей по сравнению со сложностью элементов; к - число элементов одного класса; р - количество типовых классов элементов.

Существенным преимуществом данного подхода является приоритет связей, поскольку для современных технических систем в большей степени характерны интенсивные структуры (рост числа связей), а не экстенсивные (увеличение числа элементов). Однако пользоваться формулой (2) весьма затруднительно, так как субъективные оценки S, v и в некоторой степени к не позволяют получить однозначные объективные результаты. Кроме того, учитывается только двунаправленные связи.

Следовательно, объективная количественная методика оценки сложности систем в настоящее время не разработана и представляет существенный теоретический и практический ин терес.

Разработка методики. Сложность системы возрастает как с ростом числа ее элементов, так и с увеличением числа связей между ними. Причем связи, на наш взгляд, являются более важным параметром. Это объясняется тем, что элемент, не связанный с остальными, не входит в систему, а внутренняя структура системы реализуется через связи. Каждый элемент может иметь от одной до нескольких связей (ограничения отсутствуют): управляющую, обратную информирующую, корректирующую, резервную дублирующую и т. д. Кроме того, связи могут быть однонаправленными (-►) и двунаправленными (◄—► ), одноканальными и многоканальными. Следовательно, для выбора связей в виде оценочного параметра необходимо ограничить их многообразие.

В качестве первого упрощения приведем все многообразие системных связей к простейшим одноканальным и однонаправленным. А число каналов и направленностей учитываем как соответствующее увеличение количества условных простейших связей.

Далее считаем, что при минимальном числе условных простейших связей каждый элемент системы должен быть связан только с одним соседним элементом и только одной связью. Тогда из элементарных геометрических соотношений минимальное число связей системы определяется выражением

OTmin = и - 1 ,                                          (3)

где т - число связей; п - число элементов.

Максимальным числом связей будем считать теоретический случай, когда каждый элемент системы связан одной простейшей связью со всеми остальными элементами. В этом случае наибольшее возможное число связей может быть найдено как mmax= 0,5ф-1) .(4)

Из выражений (3) и (4) найдем среднее число условных связей тср = 0,25(и - 1)(и + 2).(5)

Для сравнительных оценок более значимыми и гибкими являются относительные величины. Определим среднее возможное количество условных связей, приходящееся на один элемент системы

Si = 0,25и"'(и - 1)(и + 2).(6)

Аналогично выражению (6) сложность реальной системы оценивается по относительному числу условных связей

S = M/n.(7)

Поскольку величины St и S рассчитаны по отношению к одному элементу, то сложность любой системы может быть оценена независимо от их числа в системе.

Применение выражения (6) в качестве порогового критерия позволяет разбить все множество сравниваемых систем с одинаковыми или разными функциями и с равным или близким числом элементов на два класса: простые (S5,).

Несмотря на абсолютную объективность рассчитанных оценок сложности, определенным интуитивным ограничением разработанной методики видится то, что система из трех элементов с возможным наибольшим числом связей выглядит все-таки менее сложной, чем система из двадцати элементов с минимальным числом связей. Таким образом, необходима более детальная методика, позволяющая четче дифференцировать все множество самых разных систем.

Рассмотрим основные количественные характеристики систем, приведенные в табл. 1.

Таблица 1 Количественные характеристики систем

——-^ ^ Элементы, п Параметр         —------------		3	5	8	10	15	20	30
Число условных связей	^min	2	4	7	9	14	19	29
	^max	3	10	28	45	105	190	435
	Wcp	2,5	7,0	17,5	27	59,5	104,5	232
Показатель СЛОЖНОСТИ	Smin	0,67	0,80	0,88	0,90	0,93	0,95	0,97
		1,0	2,0	3,5	4,5	7,0	9,5	14,5
	S’cp	0,83	1,40	2,19	2,70	3,97	5,23	7,73

Анализ табличных данных позволяет сделать выводы:

• -    рост количества связей т в системах значительно опережает увеличение в них числа элементов п;

• -    в достижении наибольшего количества связей т_тах и даже близких к нему величин отсутствует практическая необходимость.

Следует отметить, что установленный порог наибольшего количества связей в системе (табл. 1) теоретически может быть превышен. Вместе с тем, в реальных системах количество связей практически всегда меньше т_тах. Это связано с неудобством и нецелесообразностью выполнения декомпозиции системы сразу на подсистемы 3, 4 и более высоких порядков. Обычно начальная декомпозиция системы осуществляется на относительно небольшое число ведущих функциональных блоков - подсистем первого порядка. В этой связи пороговый критерий может быть задан не средней величиной, а делением диапазона варьирования параметра сложности S на 10, что соответствует 10 %-ой области. Это позволяет откорректировать выражение (6)

5, = 0,05^ - 1)(и + 2) .                                 (8)

Метрика для более детального измерения сложности систем должна включать соответствующую шкалу и единицу измерений. В качестве шкал принимаем шкалы отношений, а единицами считаем параметры тип.

Всю рассматриваемую область параметров систем подразделяем на классы сложности (рис. 1) в соответствии со значениями ординаты т и абсциссы п.

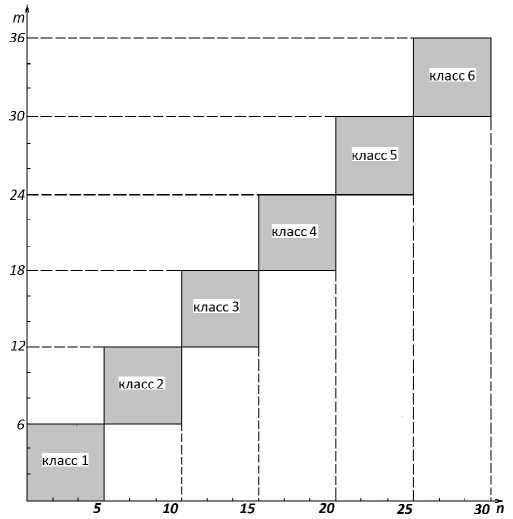
Рис. 1. Классы сложности систем

Такой выбор классов делает их в значительной степени универсальными межсистемными. Величина градаций классов равномерная по обоим параметрам. Это достигается уменьшением приращения т на 50-24 % от т_{т т}, убывающего с увеличением сложности систем, и его округлением до целых значений.

Сложность подсистем оценивается полностью независимо от системы и может отличаться от ее сложности в любую сторону. Система классов замкнута только со стороны наименьшей сложности и, при необходимости, может быть дополнена большей. Выход за границы класса хотя бы одного из параметров системы приводит к ее переходу в следующий класс сложности. Вопросы о квалиметрической адекватности и удобстве предлагаемой методики должны решать время и практика.

Рассмотрим пример оценки сложности реальных технических систем (рис. 2)

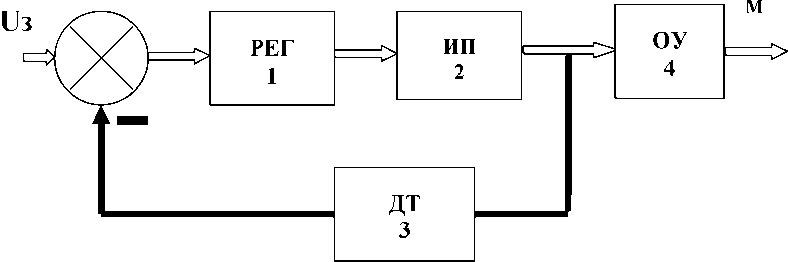
Рис. 2. Система регулирования износостойкости

Система включает 5 элементов и 5 связей. В соответствии с предлагаемой методикой она имеет первый класс сложности (п = 5, т < 10).

Более сложная система автоматического управления электрическим подвижным составом состоит из трех основных блоков (рис. 3, а). Для детализации перейдем к подсистемам следующе-

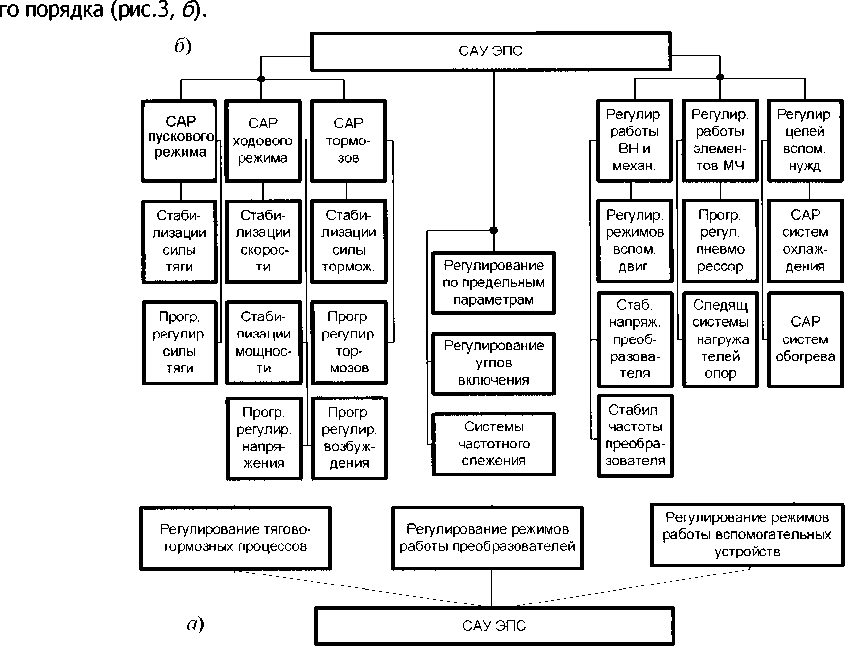
Рис. 3. Система автоматического управления электрическим подвижным составом: а-общая; б- детальная

Система (рис. 3, б) включает 25 элементов и 28 связей. Поскольку 20<и<25, а 25 <  т < 30, то систему следует отнести к пятому классу сложности.

Следует отметить, что точная оценка системы и установление ее принадлежности к определенному классу стала возможной только при декомпозиции до подсистем второго порядка.

Выводы. Разработана методика оценки сложности технических систем, включающая как объективный количественный пороговый критерий, так и систему классов их сложности.

Пороговый критерий предназначен для сравнения систем с однотипными функциями для последующего обоснованного выбора системы требуемой сложности.

По степени сложности системы разделены по шкале отношений на шесть объективно различимых классов, представляющих собой открытый и допускающий развитие со стороны роста сложности комплекс.

Проверка предлагаемой методики на реальных технических системах подтвердила ее объективность и эффективность.