Оценка содержания хлорофилла по оптической плотности листьев растений с использованием машинного обучения

ТЕХНОЛОГИИ, МАШИНЫ И ОБОРУДОВАНИЕ / TECHNOLOGIES, MACHINERY AND EQUIPMENT

EDN: updates ЕЙ® УДК / UDK 004.89:547.979.7

Хлорофилл, являясь ключевым пигментом фотосинтеза, играет центральную роль в преобразовании световой энергии в химическую, обеспечивая синтез органических веществ в растениях. Его концентрация и соотношение форм напрямую зависят от множества факторов: биотических (наличие вредителей или болезней), генетических особенностей вида растений, фазы их роста, условий окружающей среды, таких как уровень освещенности, влажность почвы, 680 Технологии, машины и оборудование ее плодородие и засоленность. В связи с этим мониторинг содержания хлорофилла (CC - Chlorophyll Content) в листьях растений представляет собой важный инструмент для оценки физиологического состояния растений, их реакции на внешние воздействия и эффективности фотосинтетических процессов. Такая информация критически важна как для научных исследований в области физиологии растений, так и для практического применения в сельском хозяйстве, особенно в контексте точного земледелия и экологического мониторинга.

Традиционные методы определения CC , основанные на лабораторном анализе экстрактов из листьев, связанные с разрушением образца, требуют значительных временных затрат и сложной подготовки проб [1]. В связи с такими ограничениями традиционные подходы становятся непригодными для оперативной и массовой диагностики состояния растений в полевых условиях. В последние годы все большее внимание уделяется разработке и внедрению неразрушающих, быстрых и экономически эффективных методов анализа, основанных на спектрофотометрии и машинном обучении ( ML – Machine Learning ) [2]. Однако применение таких методов создает ряд проблем, связанный с необходимостью повышения точности измерений, устойчивости к влиянию внешних факторов и адаптации к различным видам растений. Гиперспектральные данные имеют потенциал, однако в качестве недостатка выделяется избыточность [3].

Особый интерес вызывает интеграция спектральных измерений с алгоритмами машинного обучения, которая позволяет создавать прогнозные модели для оценки СС по данным оптической плотности листьев. Подходы, основанные на искусственных нейронных сетях (ИНС), показали свою перспективность в обработке нелинейных зависимостей и адаптации к изменяющимся условиям. Тем не менее, существующие решения часто требуют значительных вычислительных ресурсов, что ограничивает их использование в портативных устройствах [4]. Также остается недостаточно изученной возможность минимизации ошибок предсказания в широком диапазоне концентраций хлорофилла и при различных условиях освещения.

Целью данной работы является обоснование структуры ИНС и ее обучение для прогнозирования CC в листьях растений на основе данных об оптической плотности в отдельных диапазонах видимого спектра.

Задачи исследования:

– сформировать датасет на основе экспериментальных данных измерений оптической плотности листьев в синем, зеленом и красном спектральных диапазонах и соответствующих значений содержания хлорофилла;

• -    провести сравнительный анализ различных архитектур искусственной нейронной сети для выявления оптимальной структуры, обеспечивающей высокую точность прогноза;

• –    оценить точность и сходимость выбранной модели с использованием метрик MAE, MAPE и R²;

• –    провести сравнительную оценку точности разработанной нейросетевой модели с классическими алгоритмами машинного обучения (множественная линейная регрессия, метод опорных векторов, случайный лес);

  – адаптировать и реализовать выбранную модель искусственной нейронной сети в микроконтроллере портативного измерительного устройства – листового фотоколориметра.

ОБЗОР ЛИТЕРАТУРЫ

Разработка оперативного, неразрушающего метода оценки CC является важной задачей. Традиционно для изучения содержания фотосинтетических пигментов применяют спектрофотометрический метод, который основан на изучении спектра поглощения их экстрактов из листа растения. Этот метод позволяет одновременно определить содержание различных пигментов без предварительного разделения компонентов. Однако у спектрофотометрии есть ограничения: она трудоемкая, требует много времени и быстрой обработки образцов (так как пигменты быстро разрушаются), предусматривает уничтожение образцов, что препятствует динамическому наблюдению за изменениями в одних и тех же экземплярах, а также затрудняет работу с редкими видами. Эти проблемы преодолеваются с помощью бесконтактных методов оценки содержания фотосинтетических пигментов в листе непосредственно на растении с помощью портативных приборов. В живом листе у хлорофиллов более широкий и выровненный спектр поглощения, чем в растворах. Это связано с тем, что в живом листе химическая структура молекулы хлорофилла отличается от выделенного хлорофилла за счет влияния липопротеидного комплекса хлоропластов, в который они встроены¹.

Развитие дистанционных (аэрокосмических) методов значительно увеличило возможности изучения и оценки природных ресурсов по значениям вегетационных индексов, повысило качество исследований, объективность получаемых результатов, сократило временные и финансовые затраты [5]. В последние годы жизнеспособным решением для получения данных CC при мониторинге сельскохозяйственных культур и развитии точного земледелия стало гиперспектральное дистанционное зондирование [6]. Дистанционное зондирование, использующее спектры отражения растительности и вегетационные индексы, позволяет провести быстрое, эффективное, неразрушающее определение различных морфологических и биохимических признаков растений, в том числе CC [7]. Для быстрого мониторинга физиологического состояния растений по CC в различные фазы роста используются данные гиперспектральной отражательной способности листьев [8]. Показано, что объединение гиперспектральных данных дистанционного зондирования и алгоритмов ML может быть эффективным для оценки свойств растительности по СС [9].

Интеграция спектральных методов предварительной обработки с алгоритмами машинного обучения доказала свою ценность при оценке сезонной изменчивости CC. Этот подход широко применяется в точном земледелии и фенотипировании сельскохозяйственных культур [10]. Для оценки состояния растений разработаны различные методы прогнозирования СС: вегетационные индексы на основе отражения в зеленой, красной и ближней инфракрасной областях спектра; модели на основе спектральных параметров; ML [11]. Методы ML приобрели известность благодаря их применению в построении прогностических моделей для признаков растений с использованием спектральной отражательной способности. Эти методы показали заметные улучшения в точности прогнозирования и надежности моделей [12]. Подходы на основе компьютерного зрения и ML позволяют быстро и точно производить оценку CC в масштабах селекционных программ, что критически важно для точного земледелия и ускоренной селекции устойчивых сортов [13]. Комбинация гиперспектральной визуализации и ML позволяет повысить точность оценки СС за счет анализа высокоразмерных данных, автоматизировать мониторинг стресса и питания растений, масштабировать решения для крупных сельхозугодий. Спектроскопия и ML открывают новые возможности для точного, неразрушающего и экономичного мониторинга состояния выращиваемых растений, что критически важно для устойчивого сельского хозяйства и повышения урожайности [14].

Интеллектуальные системы мониторинга и управления на основе ML преобразуют традиционное сельское хозяйство в высокоточное, основанное на данных. Эти технологии позволяют в реальном времени отслеживать состояние растений и окружающей среды, обеспечивая точное орошение, удобрение и защиту от вредителей. Получаемые спектрофотометрическим методом кривые поглощения позволяют выделить из общей кривой поглощения информацию о концентрации отдельных пигментов [15]. Современные методы ML помогают своевременно диагностировать болезни растений, используя данные о СС и другие показатели. Это ускоряет реакцию на угрозы и улучшает здоровье посевов. Благодаря таким технологиям аграрии получают эффективные инструменты для контроля над состоянием растений, повышая производительность и снижая затраты ресурсов [16].

В настоящее время применяются различные приборы, такие как SPAD-502, CL-01, CCM-200, atLEAF+, позволяющие оперативно оценивать относительные концентрации пигментов без повреждения растений. Эти устройства основаны на измерении поглощения света хлорофиллом на специфичных длинах волн, при этом контроль осуществляется в инфракрасной области спектра, где поглощение минимальное, что компенсирует различия в толщине листа [17; 18]. Так, в экспериментах с томатом было установлено, что наибольшее влияние на СС оказывал уровень облученности (68 % вклад в общую вариацию), затем следовал фотопериод (15,1 %) и положение листа в кроне растения (5,7 %). В одном из экспериментов спектральный состав незначительно влиял на СС [19]. В другом эксперименте СС оказалось чувствительным к уровню освещенности и спектральному составу света. Исследование показало, что измерение СС дает возможность объективно оценивать качественные изменения в растениях, происходящих под воздействием различных факторов световой среды [20].

В научных исследованиях и практической деятельности к настоящему времени широкое распространение получили ИНС [21]. Нейросетевые технологии применяются для мониторинга состояния растений как биологических объектов, распознавания и классификации признаков дефицита питательных элементов по изображению листьев [22], оптимизации микроклимата умных теплиц [23], для определения биомассы растений по визуальному состоянию [24] и выявления заболеваний растений [25].

Предлагаемое нами техническое решение – комбинация нейросетевых методов прогноза СС по оптической плотности листа в отдельных спектральных диапазонах и использование обученной нейросети в портативном приборе – устраняет выявленные недостатки различных подходов и позволяет получать качественные результаты измерения СС в полевых условиях.

МАТЕРИАЛЫ И МЕТОДЫ

Использованы экспериментальные данные, полученные в лаборатории энергоэкологии светокультуры в ИАЭП - филиале ФГБНУ ФНАЦ ВИМ в течение 2015-2022 гг. В данный период в лаборатории исследовали оптические свойства листьев салата, перца, томата, кабачка в различных возрастных состояниях и при различных параметрах световой среды [26]. Размер объединенного датасета составлял 1 000 записей.

Для определения реальных значений СС в листе использовали прибор CCM-200 (рис. 1), принцип действия которого основан на нахождении отношения оптических плотностей листа на длинах волны 931 нм (используется для компенсации влияния толщины листа) и 653 нм (зависит от концентрации хлорофилла) [27]. Для определения оптической плотности листьев растений использовали денситометр ДП-1М (рис. 2) [28]. Использовали светофильтры группы А , с помощью которых определяли оптическую плотность листа в синем B (421-467 нм), зеленом G (511-562 нм) и красном R (607-676 нм) диапазонах.

Р и с. 1 . Измеритель содержания хлорофилла CCM-200

F i g. 1 . Chlorophyll content meter CCM-200

Р и с. 2. Определение оптической плотности листьев на приборе ДП-1М

F i g. 2. Determining the leaf optical density by the device DP-1M

Источник: фотографии 1, 2, 4 сделаны Е. Н. Ракутько при проведении измерений в лаборатории энергоэкологии светокультуры ИАЭП – филиал ФГБНУ ФНАЦ ВИМ в 2015–2025 гг.

Source: photos 1, 2, 4 were taken by Ye. N. Rakutko during the measurements in the Laboratory of Energy and Ecology Efficiency of Plant Lighting in IEEP in 2015–2025.

На рисунке 3 представлено соотношение спектров поглощения хлорофиллов (а и b) и пропускания применяемых в денситометре светофильтров. В синем и красном спектральных диапазонах полосы пропускания соответствующих светофильтров перекрываются с основными пиками поглощения хлорофиллов, что предоставляет возможность оценить их концентрацию по оптическим плотностям листа DB и DR в этих диапазонах. В зеленом диапазоне отсутствуют характерные пики поглощения хлорофиллов. Применение зеленого светофильтра по оптической плотности DG позволяет косвенно учесть другие параметры листа, не связанные с пигментами, например, его толщину. Такие спектральные соотношения дают основание полагать, что по оптической плотности листьев возможна комплексная оценка СС в них.

В качестве цифрового средства для экологического мониторинга, использующего обученную нейронную сеть для получения численных значений СС в листе растения, был взят листовой фотоколориметр, имеющий все необходимые аппаратные средства для измерения оптической плотности листа в отдельных спектральных диапазонах (рис. 4) [29]. Программное обеспечение микроконтроллера устройства реализует алгоритм предсказания СС по измеренным значениям оптической плотности листа.

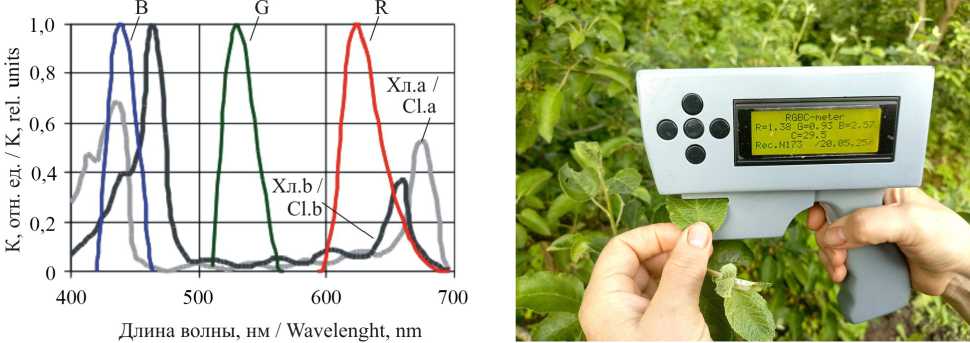
Рис. 3 . Спектры поглощения хлорофиллов и пропускания светофильтров листового фотоколориметра

Р и с. 4. Использование листового фотоколориметра для прогнозирования СС в листьях

Fig. 3 . Absorption spectra of chlorophylls and transmittance of light filters of a photocolorimeter leaves

Fig. 4. Using a photocolorimeter for leaves to predict leaf СС

Примечание: B – кривая пропускания синего светофильтра; G – кривая пропускания зеленого светофильтра; R - кривая пропускания красного светофильтра; Хл. a - спектр поглощения хлорофилла а ; Хл. b – спектр поглощения хлорофилла b .

Note: B – blue filter transmission curve; G – green filter transmission curve; R – red filter transmission curve; Chl. a – chlorophyll a absorption spectrum; Chl. b – chlorophyll b absorption spectrum.

Источник: рисунки 3, 5–10 составлены авторами статьи.

Source: figures 3, 5–10 are compiled by the authors of the article.

Произведены эксперименты со структурой ИНС путем изменения гиперпараметров в коде (количества нейронов в скрытых слоях). На рисунке 5 показана структура сети с двумя скрытыми слоями по четыре нейрона в каждом.

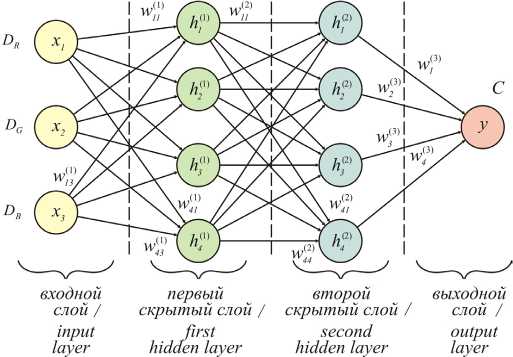
Рис. 5. Структура искусственной нейронной сети Fig. 5. Structure of an artificial neural network

Примечание: D _R , D _G , D _B – оптическая плотность листа соответственно в красном, зеленом и синем диапазоне; x _1, x _{2 ,} x ₃ – входные признаки; h l ¹, h™, h™, h? – выходные сигналы нейронов первого скрытого слоя; hfi, hfi, hfi, hfi — выходные сигналы нейронов второго скрытого слоя; у - целевая переменная; С - прогноз содержания хлорофилла; W 1 I) , W 1 3\ W^¹, W 3 - весовые коэффициенты нейронов первого слоя; W^¹, W^¹, Wfi¹ — весовые коэффициенты нейронов второго слоя; Wf³¹, W^³¹, W^³¹, W4¹³¹ — весовые коэффициенты нейронов выходного слоя.

Note: D_R , D_G , D_B – leaf optical density in the red, green, and blue spectral ranges, respectively; x , x 2 x 3 - input features; hfi, hfi,hfi,hfi - output signals of the neurons in the first hidden layer; h²\ hfi, hfi, hfi - output signals of the neurons in the second hidden layer; у - target variable; С -predicted chlorophyll content; Wfi, W ^¹ , W 41 , W j ) - weight coefficients of the first layer neurons; Wn*, W 42 , W )^ - weight coefficients of the second layer neurons; Wl³¹, Wfi, Wfi, W 4^{3 1} - weight coefficients of the output layer neurons.

Результатом обучения сети являются матрицы весов между входным и первым скрытым слоем W ⁽¹⁾, между первым и вторым скрытыми слоями W ⁽²⁾, между вторым скрытым и выходным слоем W ⁽³⁾, смещений ( bias ) для нейронов соответствующих слоев B ⁽¹⁾, B ⁽²⁾ и B ⁽³⁾ (на структуре не показаны). При переносе значений матриц в микропроцессорное устройство, аппаратно измеряющее элементы входного вектора X , программно реализуются вычисления:

h <1 = ^ (W d’ X + B⁽¹⁾); h <²⁾ = ^ (W <²⁾ h + B <²’); y = a out W ® h ⁽²⁾ + B <³’), где σ, σ _out – соответствующие функции активации.

Вычисленное значение y представляет собой предсказание СС , соответствующее измеренным значениям оптической плотности листа D_R , D_G и D_B .

Каждый слой линейного стека имеет один входной и один выходной тензор. Скрытые слои полносвязные. Для придания нелинейности модели применена функция активации ReLU (Rectified Linear Unit). Выходной слой содержит один нейрон, так как предсказывается одно значение СС (C,pred) без функции активации. Применяется оптимизатор Adam, который учитывает предыдущие градиенты для ускорения сходимости, адаптивно настраивает скорости обучения для каждого параметра и хорошо работает с регрессией. Для обучения и оценки моделей исходный датасет был случайным образом разделен на обучающую и тестовую (валидационную) выборки в соотношении 80/20. Таким образом, для обучения модели использовалось 800 примеров, а для независимой проверки ее обобщающей способности 200 примеров. Перед разделением данные были перемешаны для обеспечения репрезентативности распределения целевой переменной (содержания хлорофилла) в обеих выборках. Данный прием позволил избежать переобучения и получить объективную оценку производительности модели на новых, не участвовавших в обучении данных.

Задавали 100 эпох – итераций полного прохода по всем обучающим данным. С помощью метрики средней абсолютной ошибки ( MAE – Mean Absolute Error ) определяли насколько в среднем (по n примерам в тестовом наборе) предсказания C_i^pred отличаются от реальных значений C_i^true . Особенности MAE : линейная чувствительность к ошибкам, более легкая интерпретируемость (это средняя абсолютная ошибка в единицах целевой переменной), меньшая чувствительность к выбросам.

В качестве функции потерь приняли среднюю квадратичную ошибку ( MSE – Mean Squared Error ). Особенности принятой функции потерь MSE : сильно штрафует большие ошибки (квадратичная зависимость), оптимальна для задач регрессии с нормальным распределением ошибок, чувствительна к выбросам. Вычисляли среднюю ошибку предсказаний ( MAPE – Mean Absolute Percentage Error ). Разброс данных характеризовали стандартным отклонением ( SD ).

Предварительная обработка и визуализация данных велась в Excel. Для построения и обучения ИНС использовалась облачная среда Google Colab, предоставляющая бесплатный доступ к вычислительным ресурсам ( GPU / TPU ).

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

На рисунке 6 показана связь СС и оптической плотности листьев в отдельных спектральных диапазонах (по результатам измерений).

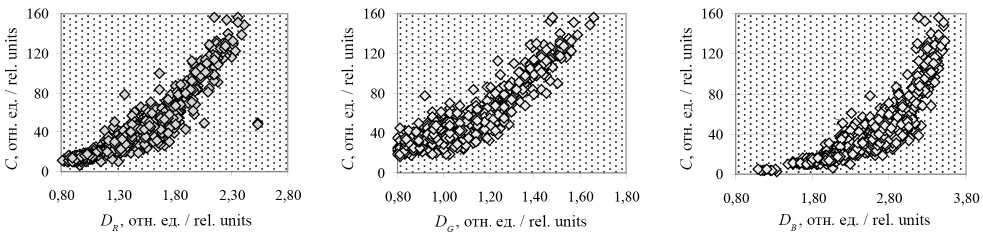
Рис. 6. Связь СС ( С и оптической плотности листа в красном D R , синем D_G и зеленом D_B диапазонах

Fig. 6. Relationship between СС ( С) and leaf optical density in red D R , green D_G and blue D_B ranges, relative units

Анализ первичной информации об оптической плотности листьев в отдельных спектральных диапазонах и соответствующих им значениям СС позволил выявить следующие закономерности.

Экспериментальные данные свидетельствуют о нелинейной связи СС и оптической плотности листа в разных спектральных диапазонах. Эта нелинейность обусловлена природой взаимодействия света с веществом листа, включающей поглощение и рассеивание электромагнитного излучения пигментами. Особенно ярко проявляется нелинейность в красной области спектра (рис. 3).

Оптическая плотность листьев в красной области D_R варьируется от 0,57 до 2,54 ( SD = 0,35), зеленой D_G от 0,9 до 1,66 ( SD = 0,24), синей D_B от 1,09 до 3,53 ( SD = 0,47) отн. ед. Соответственно этим комбинациям значение С меняется от 3,1 до 156,5 ( SD = 28,89) отн. ед. Такой широкий диапазон вызван различной толщиной листа, неоднородностью его строения, различиями в составе клеточной стенки, плотности тканей и распределением пигментов у различных растений, использованных в эксперименте.

Результаты экспериментов со структурой ИНС, при которых изменяли количество скрытных слоев, сведены в таблицу 1. Помимо рассмотренных выше метрик, таблица содержит количество весов нейронов N (включая нейроны смещения), а также размер необходимой памяти V (при сохранении весов в формате float ).

Для демонстрации эффективности предложенного подхода с ИНС была проведена сравнительная оценка с рядом классических алгоритмов машинного обучения. В качестве альтернативных моделей выбраны множественная линейная регрессия ( Linear Regression ), метод опорных векторов для регрессии ( SVR - Support Vector Regression ) и алгоритм ансамблевого обучения – случайный лес ( Random Forest ). Все модели обучались и тестировались на одном и том же разделенном наборе данных. Результаты сравнения представлены в таблице 2.

Т а б л и ц а 1

T a b l e 1

Показатели искусственной нейронной сети с различной структурой скрытых слоев Performance of artificial neural network with different hidden layer structure

Структура / Structure	MAE, отн. ед. / rel. units	R2 , отн.ед. / rel. units	MAPE , %	N , шт. / number	V , байт / bytes
64:64	6,75	0,8862	17,02	4 481	17 924
32:32	6,64	0,8886	16,34	1 217	4 868
16:16	6,71	0,8867	17,05	353	1 412
8:8	6,80	0,8837	17,14	113	452
4:4	6,83	0,8808	16,86	41	164
4:0	8,21	0,8508	21,68	21	84

Из таблицы 2 видно, что предложенная ИНС с архитектурой «4:4» превзошла все сравниваемые модели по всем метрикам, показав наименьшую среднюю абсолютную ошибку ( MAE ) и среднюю абсолютную процентную ошибку ( MAPE ), а также наибольший коэффициент детерминации ( R ²). Это свидетельствует о ее способности эффективнее улавливать нелинейные взаимосвязи между оптической плотностью и содержанием хлорофилла по сравнению с линейными и ансамблевыми методами.

Т а б л и ц а 2

T a b l e 2

Сравнительный анализ моделей машинного обучения для прогнозирования содержания хлорофилла

Comparative analysis of machine learning models for chlorophyll content prediction

Модель / model	MAE , отн. ед. / rel. units	R2 , отн.ед. / rel. units	MAPE , %
Множественная линейная регрессия / Linear Regression	12,45	0,7215	28,91
Случайный лес / Random Forest	8,03	0,8612	19,54
Метод опорных векторов / Support Vector Regression	9,87	0,8103	23,12
ИНС 4:4 / ANN 4:4	6,83	0,8808	16,86

На рисунке 7 представлены графики обучающих и валидационных потерь при работе ИНС, построенные в следующих координатах: ось X – номер эпохи; ось Y – значение функции потерь MSE . Графики показывают динамику изменения ошибки модели в процессе обучения.

Смоделировано шесть конфигураций ИНС, начиная от глубокой сети с двумя скрытыми слоями по 64 нейрона («64:64» согласно таблице) и заканчивая простой однослойной сетью с четырьмя нейронами («4:0»). Все сети имеют три входных и один выходной признак. Средняя абсолютная ошибка MAE = 6,64 отн. ед. достигает минимума при архитектуре «32:32». При этом средняя относительная ошибка MAPE = 16,34 % наименьшая, коэффициент детерминации R ² = 0,8886 максимален. Хуже себя проявляет самый простой вариант с одним скрытым слоем из четырех нейронов («4:0»), где MAE = 8,21 отн. ед., R ² = 0,8508, MAPE = 21,68 %.

Количество параметров (весов) N непосредственно зависит от количества нейронов в структуре. Чем меньше нейронов, тем меньше параметров хранится в памяти микроконтроллера. Модель «4:0» содержит минимум параметров (всего 21 вес), тогда как сеть «64:64» насчитывает почти в 213 раз больше (4 481 вес). Для хранения параметров сети «4:0» требуется всего 84 байта, тогда как для сети «64:64» потребуется 17 924 байт.

Наиболее сбалансированная комбинация ошибок и сложности наблюдается при структуре «32:32». Следующая структура по критерию меньшего значения MAPE – сеть «4:4». Ее MAPE всего на 0,52 %, а MAE на 0,19 % выше, чем у структуры «32:32». Однако она существенно менее требовательна по объему требуемой памяти, что может быть критично для применения сети в простых микроконтроллерах типа Arduino.

Для реализации на микропроцессорном устройстве остановились на структуре ИНС «4:4». Графики обучающих и валидационных потерь показывают, что после 20-й эпохи потери резко уменьшились примерно с 3 000 до 200 отн. ед. Такое поведение характерно для большинства нейронных сетей, где начальная случайная инициализация весов постепенно приближается к оптимальному решению. Высокие начальные значения потерь связаны с большим расхождением начальных предсказаний модели и реальных данных, которое быстро исправляется процессом обучения. Тот факт, что графики потерь на тренировочном и контрольном наборах практически совпадают и остаются близкими друг другу на протяжении всей процедуры обучения, свидетельствует о хорошем поведении модели. Значительно

^® ИНЖЕНЕРНЫЕ ТЕХНОЛОГИИ И СИСТЕМЫ Том 35, № 4. 2025 более высокие потери указывают на переобучение модели, но в данном случае разницы практически нет, значит, модель успешно экстраполирует знания на новые данные. Параллельный ход обоих графиков вдоль горизонтальной оси означает, что дальнейшее обучение практически не улучшает результаты. Оптимизатор уже находится в точке локального минимума, модель достигает своего предела обобщаемости на предоставленном наборе данных. Дальнейшее уменьшение потерь маловероятно без существенного улучшения архитектуры или увеличения набора данных.

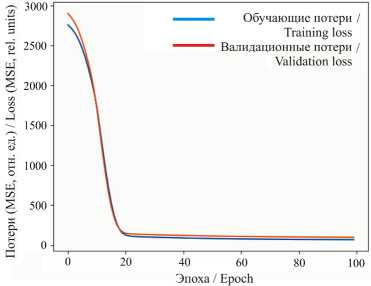
Р и с. 7. Обучающая и валидационная потери

F i g. 7. Training and validation loss

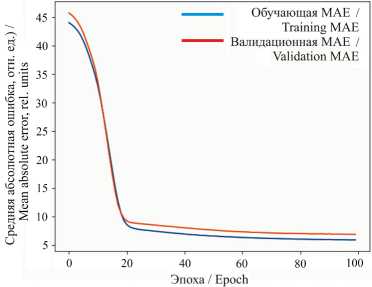
Р и с. 8. Обучающая и валидационная ошибки

F i g. 8. Training and validation MAE

На рисунке 8 представлены графики обучающей и валидационной ошибки. Средня абсолютная ошибка MAE = 6,83 отн. ед.

Динамика средних абсолютных ошибок повторяет картину, рассмотренную выше для среднеквадратичной ошибки. Начальное падение MAE аналогично снижению MSE , демонстрирует стремительное улучшение предсказательных способностей модели в первые этапы обучения. Такая динамика связана с постепенным выходом из начальной хаотичности в сторону оптимального положения весов сети и ее способности хорошо обобщаться на неизвестные данные. Небольшое устойчивое снижение MAE после первого этапа обучения свидетельствует о медленном продвижении к лучшему состоянию. Здесь возможна остановка процесса обучения раньше, если расходы на ресурсы превышают пользу от небольших улучшений. Данные графики дополняют предыдущий анализ и укрепляют уверенность в достигнутом результате.

На рисунке 9 фактические значения (True Values) сопоставляются с предсказанными (Predicted Values). Рассмотрение графика сопоставления истинных значений СС и предсказанных моделью дает важные сведения о точности и надежности разработанной модели. Большая часть точек расположена вблизи диагональной прямой, что свидетельствует о хорошем совпадении предсказанных значений с реальными. Чем ближе точка к диагонали, тем точнее работа модели. Скопление точек в нижней части графика (первая треть диапазона изменения СС) указывает на лучшее качество предсказаний для образцов с низким уровнем хлорофилла. Вместе с анализом первичных данных (рис. 6) это свидетельствует о том, что листья с низким СС были представлены в большем количестве в исходном наборе данных или имели большую однородность, облегчающую обучение модели. Отдельные точки располагаются далеко от диагонали, что указывает на наличие значимых ошибок в предсказаниях. Причины могут включать плохую репрезентативность таких случаев в обучающем наборе, трудности распознавания сложных ситуаций или аномалии в данных. Возможно, в модель необходимо включить дополнительные входные признаки, такие как вид растения и физически измеряемую толщину листа. В целом модель работает удовлетворительно, особенно для малых значений СС, но требует доработки для повышения точности предсказаний в полном диапазоне возможных значений.

На рисунке 10 представлен график распределения ошибок предсказания, имеющий вид нормального распределения с центром в районе нулевого значения, что свидетельствует о ряде положительных качеств модели.

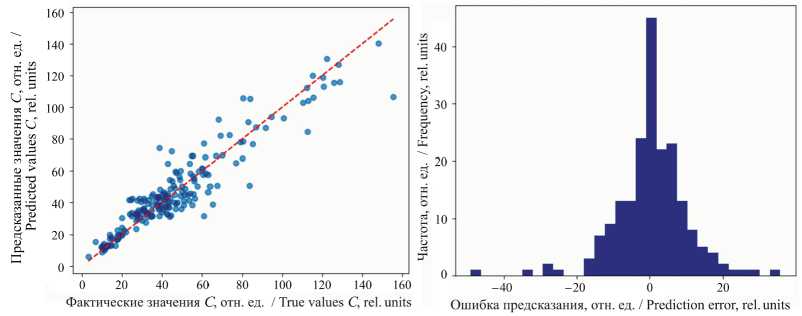
Р и с. 9. Сопоставление фактических и предсказанных значений

F i g. 9. True vs predicted values

Р и с. 1 0. График распределения ошибок предсказания

F i g. 1 0. The graph of prediction error distribution

Форма кривой указывает на хорошую статистику обученной модели. Симметричность и центрирование пика около нуля предполагают, что большинство ошибок невелики и сконцентрированы около среднего значения. Это важный аспект, подтверждающий устойчивость и правильность работы модели. Пик кривой располагается около нулевых ошибок, его величина указывает на значительную долю успешных предсказаний с малой ошибкой. Подавляющее большинство ошибок находится в пределах диапазона ±20 отн. ед. Присутствие редких выбросов на краях графика подразумевает существование небольшого процента крупных ошибок. Такие исключения важны для понимания источников систематических сбоев модели и требуют отдельного анализа. Наблюдаемая картина распределения ошибок свидетельствует о приемлемом уровне качества модели, что обеспечит надежность и применимость модели в практических целях.

На рисунке 11 представлен график остатков, в котором сравнивается разница между предсказанными и действительными значениями СС , что помогает диагностировать качество модели, выявляет ее сильные и слабые стороны. Их случайное и несмещенное распределение относительно нуля соответствует одному из ключевых статистических предположений регрессионного анализа.

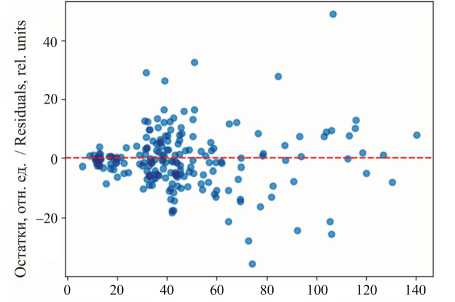
Предсказанные значения, отн. ед. / Predicted values, rel. units

Р и с. 11. График остатков F i g. 11. Residuals graph

Распределение точек близко к горизонтальной нулевой линии свидетельствует о правильном направлении работы модели. Большинство остатков стремятся к нулю, что указывает на малые ошибки предсказания. Преобладание точек в диапазоне низких значений СС говорит о лучшей точности модели при прогнозировании в этой области. Несколько точек заметно удаляются от нулевой линии, демонстрируя значительные ошибки предсказания. Равномерное распределение отрицательных и положительных остатков по обе стороны от нулевой линии поддерживает предположение о независимости ошибок от направлений (нет смещения в положительную или отрицательную сторону). Ограниченный диапазон колебаний остатков вокруг нуля указывает на хороший баланс модели, сводящий риск серьезных ошибок к минимуму.

ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ

Результаты исследования демонстрируют возможность создания компактной и достаточно точной модели, способной работать в реальном времени и обеспечивать объективную оценку физиологического состояния растений. Это имеет значение не только для совершенствования методов экологического мониторинга, но и для поддержки принятия решений при управлении культивированием растений, особенно в условиях изменения климатических параметров и необходимости повышения устойчивости аграрных систем. Предлагаемый подход может быть использован в цифровых агротехнологиях, направленных на оптимизацию режимов выращивания растений, повышение продуктивности и снижение антропогенной нагрузки на окружающую среду.

В ходе проведенного исследования обоснована структура и обучена ИНС для прогнозирования СС в листьях растений на основе данных об их оптической плотности в отдельных диапазонах видимого спектра. Предложенная модель демонстрирует достаточную точность при минимальных вычислительных затратах, что позволяет реализовать ее в микроконтроллерном устройстве – листовом фотоколориметре. Таким образом, поставленная цель – создание эффективного инструмента для быстрой и неразрушающей оценки физиологического состояния растений – достигнута.

Наиболее точной среди исследованных архитектур оказалась сеть «32:32», обеспечившая коэффициент детерминации R ² = 0,8886 и среднюю абсолютную ошибку MAE = 6,64 относительных единиц. Однако для практического применения в условиях ограниченных вычислительных ресурсов выбрана упрощенная структура «4:4», которая сохранила приемлемый уровень точности ( R ² = 0,8808, MAE = 6,83) при значительном снижении объема используемой памяти и количества параметров модели. Это позволило адаптировать нейросеть под аппаратные ограничения портативного устройства, расширив тем самым возможности ее применения в полевых условиях.

Полученные результаты подтверждают перспективность использования машинного обучения в задачах неразрушающего анализа состояния растений. В отличие от традиционных методов, требующих длительной подготовки образцов и их разрушения, предложенный подход обеспечивает оперативное получение информации, необходимой для принятия решений в управлении агротехноло-гическими процессами. Кроме того, использование ИНС позволило повысить точность прогноза по сравнению с классическими эмпирическими моделями, особенно в условиях неоднородности исходных данных.

Анализ графиков ошибок и остатков показал, что модель устойчива к случайным отклонениям и демонстрирует хорошие обобщающие способности. Особенно высокая точность наблюдается при оценке образцов с низким и средним уровнем СС , что делает модель актуальной для диагностики стрессовых состояний растений, связанных с недостатком питательных веществ или воздействием неблагоприятных факторов окружающей среды.

Предложены гипотезы о возможных причинах крупных ошибок предсказания:

• 1.    Биологическая вариабельность. Наибольшие ошибки могли быть связаны с образцами, имеющими атипичное анатомическое строение (например, аномальная толщина кутикулы, губчатой ткани или наличие опушения), которое не полностью учитывается тремя измеряемыми спектральными каналами.

• 2.    Неучтенные факторы. На содержание хлорофилла и оптические свойства могут влиять физиологическое состояние растения (водный стресс, начало цветения), не регистрируемое напрямую прибором, а также видовые особенности, не закодированные явно в модели.

• 3.    Ограниченность данных. Выбросы могут соответствовать редким комбинациям входных параметров, недостаточно представленным в обучающей выборке, что приводит к ухудшению обобщающей способности модели в этих «слепых зонах».

Для минимизации подобных ошибок в будущем планируется расширить да-тасет, включив в него больше образцов с экстремальными значениями, а также рассмотреть добавление дополнительных входных признаков, таких как вид растения и объективно измеряемая толщина листа.

Результаты работы имеют важное практическое значение для развития цифровых технологий в сельском хозяйстве. Разработанное устройство может быть использовано как часть систем экологического мониторинга, управления удобрением и поливом, а также в программе фенотипирования сельскохозяйственных культур. Его внедрение позволит повысить точность аграрных технологий, снизить антропогенную нагрузку на окружающую среду и увеличить урожайность сельскохозяйственных культур.

Перспективы масштабирования разработанной модели на другие виды растений и агроклиматические условия являются обнадеживающими, но требуют дополнительной валидации. Универсальность подхода обеспечивается тем, что в основе модели лежат фундаментальные физические принципы – поглощение света пигментами хлорофилла в синей и красной областях спектра, что характерно для всех высших растений. Однако для достижения высокой точности на новых культурах (например, злаках или плодовых деревьях) может потребоваться дообучение модели на репрезентативных данных для этих видов. Это позволит алгоритму адаптироваться к специфике морфологии листа (толщина, восковой налет) и характерным диапазонам содержания хлорофилла. Текущая модель, обученная на данных по салату, перцу, томату и кабачку, уже демонстрирует хорошую обобщающую способность в пределах близких видов. Дальнейшие исследования будут направлены на проверку переносимости модели и разработку процедуры ее быстрой калибровки под новые условия.

Предложенная модель предназначена для реализации в микроконтроллерном устройстве – листовом фотоколориметре, что открывает возможности для ее использования в мобильных системах мониторинга и управления агротехническими процессами. Особое внимание уделено балансу между точностью предсказаний и вычислительной эффективностью модели, что делает ее пригодной для практического применения даже в условиях ограниченных аппаратных ресурсов.

Перспективы дальнейших исследований связаны с улучшением точности модели за счет расширения датасета, введения дополнительных входных параметров (например, толщины листа или вида растения), а также перехода к мультиспек-тральному анализу. Также целесообразно продолжить работу по минимизации модели без потери качества прогноза, чтобы обеспечить ее функционирование на более простых и доступных контроллерах. Повышение информативности измерений и расширение возможностей автоматической интерпретации данных открывает новые горизонты для интеграции цифровых решений в современное сельское хозяйство.

Таким образом, применение методов машинного обучения в сочетании с компактными измерительными устройствами открывает реальные пути к созданию интеллектуальных систем мониторинга и управления состоянием растений, которые станут основой устойчивого и высокотехнологичного агропроизводства будущего.