Оценка состояния объекта по регрессионным зависимостям при прогнозировании входных параметров

m – количество параметров. Алгоритм моделирования и прогнозирования состояния технического объекта состоит из следующих этапов:

– построение моделей входных параметров объекта, образующих систему временных рядов X 1 , X ₂,..., X m , на основе методологии адаптивного динамического регрессионного моделирования [4-6];

– прогнозирование по полученным моделям временных рядов значений входных параметров исследуемого объекта;

– построение регрессионной зависимости f ( X 1 , X ₂, . , X m ) , характеризующей связь между состоянием объекта Y и его входных параметров Х j = 1, m ;

– использование полученной регрессии и спрогнозированных значений входных параметров для прогнозирования состояния технического объекта.

Согласно методологии динамического регрессионного моделирования временной ряд представляется в виде суммы составляющих:

y(t) = f ⁽ t ) + g ⁽ t ) W^(t ) + ^ ⁽ t ) ,      ⁽¹⁾

где y(t) - значения временного ряда, фикси руемые в моменты времени t = 1,2,. _, n; f (t) – неслучайная (долговременная) функция тренда; g (t) - неслучайная периодическая функция; ^(t) - случайная с элементами регулярности функция; ^(t) - нерегулярная компонента (случайная величина, ошибка).

При выявлении значимой регулярности процесса методами фрактального и мультифрак-тального анализов [7] выделяется функция тренда f ( t ) . Далее остатки исследуются на существование периодических компонент при помощи гармонического анализа и других методов. Остаточные колебания после выделения неслучайных функций сглаживаются случайной с элементами регулярности функцией ^ ( t ) . В качестве данной функции могут выступать либо авторегрессионная модель подходящего порядка, либо смешанная модель авторегрессии-скользящего среднего (АРСС), либо одна из комплекса авторегрессионных моделей с условной гетероскедастичностью (ARCH) [8], либо последовательное применение этих подходов.

После структурно-параметрической идентификации модели временного ряда проверяется соблюдение условий применения регрессионного анализа: постоянство дисперсии, независимость регрессоров, нормальность распределения ошибок, нулевое значение математического ожидания ошибок, независимость ошибок. При нарушении этих условий используются специ- альные методы адаптации [4]. Если основные условия соблюдаются, построенная комплексная модель временного ряда может быть использована для прогнозирования. После получения предсказанных значений входных параметров по моделям временных рядов, строятся регрессионные зависимости выходных характеристик объекта в зависимости от входных (регрессоров).

При неоднородности физических свойств объекта на области значений регрессоров, «глобальные» модели часто обладают недостаточно высокой точностью. В этом случае предлагается применять принцип «кусочности» или локальности модели, то есть вариации её параметров по области значений регрессоров. В качестве прогнозирующей зависимости можно использовать кусочно-линейную регрессию с разрывом по отклику и с добавлением элемента авторегрессии для учёта значения отклика в предыдущие дни. При этом свободный коэффициент в модель предполагается не включать. В этом случае регрессионная модель представляется в виде:

Y ( t ) = в X 1 + в 21 X 2 + ... + в т1 X m + в т + 1,1 Y ( t — W ( t ) <  С ) + ( в 12 X 1 + в 22 X 2 + ... + в т 2 X m + в т + 1,2 Y ( t — 1))( Y ( t ) >  С )

где m - количество регрессоров модели; к - порядок авторегрессии; c - точка разрыва; ( Y ( t ) <  c ), ( Y ( t ) >  c ) - логические выражения, принимающие значения: 1 - если истинно, 0 -если ложно; Y ( t-1 ) ... Y ( t-k ) - значение отклика в предыдущие моменты времени. Фактически данная модель состоит из двух регрессий, каждая из которых применяется для определённого уровня отклика.

Одним из ключевых моментов при использовании кусочных регрессий является способ отнесения текущих данных к нужному «куску». Предлагается следующий алгоритм этой процедуры. Вначале вычисляется прогноз по обеим регрессиям. Затем полученные результаты сравниваются со значением в точке разрыва. Если прогноз по первому куску меньше либо равен значению в точке разрыва, а прогноз по второму куску - больше, то за итоговый результат принимается среднее арифметическое данных чисел. Если хотя бы для одного куска наблюдается «нарушение», то итоговым значением считается прогноз по тому куску, для которого выполняется неравенство. Если же условия нарушаются для обоих случаев, то также вычисляется среднее арифметическое.

Например, имеется кусочно-линейная регрессия:

Y = Y • (Y < c) + Y2 • (Y > c),                (3)

где           Y 1 = ⁽ b 01 ^{+ b} 11 • X 1 ⁺ -⁺ b m 1 • X m ) i

Y 2 = ⁽ b 02 ⁺ b 12 • X 1 ⁺ — ⁺ b m 2 • X m ) ? c ^- точка разрыва.

Пусть на основе регрессий Y 1 и Y 2 получены прогнозы Y и Y ₂, причём Y <  c и Y ₂<  c . В данном случае наблюдается нарушение для второй регрессии, поэтому за итоговый прогноз берётся Y . По полученной модели кусочнолинейной регрессии с добавлением элемента авторегрессии и спрогнозированным значениям входных параметров прогнозируется будущее состояние технического объекта с целью формирования сигнала о возможной аварийной ситуации. Эффективность разработанной методики прогнозирования состояния технического объекта иллюстрируется на примере моделирования выходной характеристики объекта Y и множества входных параметров, образующих временные ряды X , X ₂,..., X₇ по результатам 35 наблюдений. Для системы временных рядов (входных параметров объекта) согласно методологии адаптивного динамического регрессионного моделирования построены следующие модели:

X ( t ) = 0,47715 • X ( t - 1) + 0,60453 • X ( t - 2) ,

X^ ( t ) = 0,89898 • X ₂ ( t - 1) + 0,09956 • X ₂ ( t - 2) , X ₃ ( t ) = 0,79444 • X ₃ ( t - 1) + 0,17374 • X ₃ ( t - 2) , X ₄ ( t ) = 0,57316 • X ₄ ( t - 1) + 0,42619 • X ₄ ( t - 2), X ₅ ( t ) = 0,87087 • X ₅ ( t - 1) + 0,12289 • X ₅ ( t - 2) , X ₆ ( t ) = 0,57535 • X ₆ ( t - 1) + 0,41826 • X ₆ ( t - 2) ,

X ₇ ( t ) = 0,90417 • X ₇ ( t - 1) + 0,09523 • X ₇ ( t - 2) .

По полученным моделям временных рядов выполнен прогноз на четыре наблюдения. Для выходного параметра объекта Y построена кусочно-линейная регрессия с авторегрессией 1-го порядка (КЛР-АР(1)):

Y ( t ) = ( - 0,002228 • X 1 - 0,034335 • X ₂ + 0,028101 X 3 - 0,295028 • X ₄ + 0,505128 • X ₅ + + 0,031676 • X ₆ + 0,433677 • X ₇ + 0,787707 • Y ( t - 1)) • ( Y ( t ) <  1,0109) + ( - 0,028096 • X 1 -- 0,049394 • X ₂ + 0,046701 • X ₃ - 0,208433 • X ₄ + 1,182003 • X ₅ + 0,010884 • X ₆ + + 0,520216 • X ₇ - 0,110927 • Y ( t - 1)) • ( Y ( t ) >  1,0109)

С использованием полученной регрессии и спрогнозированных значений входных параметров X_Y , X ₂,..., X₇ выполнен прогноз выходной характеристики объекта Y на четыре наблюдения. На рис. 1 показан смоделированный временной ряд, а на рис. 2 - соответствующий прогноз на 4 измерения. Сплошной линией показаны опытные данные, штриховой - расчетные.

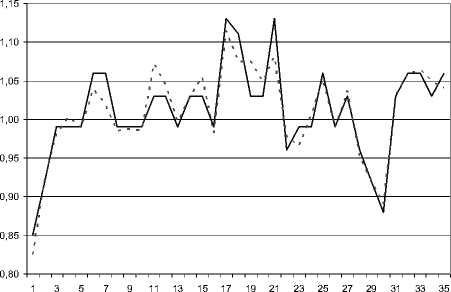
Рис. 1. Моделирование на основе КЛР-АР(1)

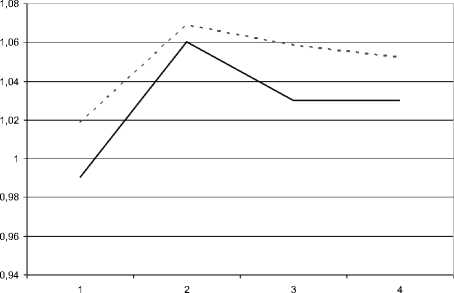
Рис. 2. Прогнозирование состояния объекта на основе КЛР-АР(1)

Для сравнительного анализа эффективности предлагаемой методики прогнозирования выходных характеристик объекта по той же выборке были построены модели множественной линейной регрессии (ЛР) и множественной линейной регрессии с добавлением элемента авторегрессии 1-го порядка (ЛР-АР(1)):

Y ( t ) = - 13,604 + 0,0112 • X 1 - 0,4476 • X ₂ + 0,0422 • X ₃ - 0,3325 • X ₄ + 1,1932 • X ₅

+ 0,0216 • X ₆ + 4,5121 • X₇

Y ( t ) = - 19,6682 - 0,0011 • X 1 - 0,6002 • X ₂ + 0,0367 • X ₃ - 0,2679 • X ₄ + X ₅ + 0,0229 • X ₆ + 6,0737 • X ₇ + 0,3024 • Y ( t - 1)

В табл. 1 представлены результаты сравнения кусочно-линейной модели с ЛР и ЛР-АР(1) по точности прогнозирования. В первом столбце таблицы представлены исходные значения отклика Y; в следующих столбцах для каждой модели представлены значения  спрогнозирован ных значений отклика Y (прогноз), а также ошибка прогноза в процентах, вычисляемая по формуле (7). ˆ e = |-у-| -100%,        (7)

где Y - исходное значение отклика; Y - прогнозное значение отклика.

По данным таблицы следует, что при использовании модели кусочно-линейной регрессии с авторегрессией 1-го порядка точность прогнозирования существенно повышается по сравнению с моделями обычной множественной линейной регрессии и множественной линейной регрессии с добавлением элемента авторегрессии 1-го порядка.

Таблица 1. Сравнение моделей по точности прогнозирования

Исходные значения отклика Y	Модель регрессии
	КЛР-АР(1)		ЛР		ЛР-АР(1)
	прогноз	ошибка, %	прогноз	ошибка, %	прогноз	ошибка, %
0,99	1,02	2,87	0,97	1,75	1,27	28,77
1,06	1,07	0,84	0,60	43,82	0,81	24,05
1,03	1,06	2,76	0,58	43,48	0,64	37,44
1,03	1,05	2,14	0,61	40,75	0,63	39,24

Выводы: использование кусочно-линейных моделей регрессии позволяет повысить точность прогнозирования состояния технического объекта. Безусловным преимуществом кусочнолинейных регрессий относительно обычных линейных регрессий является учёт неоднородности свойств объекта за счёт своей «кусочности» и вариации уровней отклика. Это позволяет более точно моделировать и прогнозировать процесс, в особенности, когда поступающие данные отличаются значительной нестабильностью значений.

Работа выполнена в рамках задания Минобрнауки России №2014/232.