Оценка стабильности вибраций на основе алгоритма обобщенной дисперсии

многомерного нормального распределения с последующей проверкой параметров: вектора математических ожиданий и ковариационной матрицы. В качестве исходных данных используются показатели реального процесса. Основные нарушения процесса - скачкообразное и постепенное увеличение рассеяния вибраций.

Пусть в процессе контролируется множество р показателей вибраций Х ₁, Х ₂, …, Х_р . Через определенные (как правило, равные) промежутки времени берутся выборки из n наблюдений ( n – объем мгновенной выборки, n = 1…10).

С целью оценки параметров контроля всего берется m выборок. По общей (обучающей) выборке nm наблюдений оценивается вектор T средних Ц0 — (ft,Ц2,...,Цр) и ковариационная матрица S. Оценки компонент вектора средних:

| m n

Ц ) = —ЕЕ x ijt , ^j = i- р ,     (1)

mn t _{= 1} i _{= 1}

( x_ijt – результат i -го наблюдения в t -й выборке по j -му параметру; i — 1... n ; t — 1... m );

оценки элементов ковариационной матрицы S:

1 m n sjk =         ЕЕ ^xyt- Pj)(xikt—Pk) - m (n 1) t=1 i=1

j = 1... p , k = 1... p .

Известия Самарского научного центра Российской академии наук, т. 20, № 4(3), 2018

Предполагается, что выборка взята из генеральной совокупности с многомерным нормальным распределением. Для моделирования выборок можно использовать алгоритм генерирования псевдослучайных нормальных векторов [8-10].

Предположим, что совокупность случайных величин Z _t имеет стандартное нормальное распределение с параметрами (0,1). Тогда значения X_t , распределенные по многомерному нормальному закону с вектором средних m и ковариационной матрицей S, могут быть найдены с помощью линейного преобразования:

X T = AZ T + M , где А - нижняя треугольная матрица

^a 1      ⁰

A =

a ₂₁

a ₂

a p 1 a p 2

...

a p

коэффициенты a jk которой определяются рекуррентной процедурой:

j - 1

s— 7 а, а jk           kr jr a,k = , r=1       ; 1 ^ k ^ j ^ Р (5)

^jk               j - 1

J sjj- L ar r=1

(значения s k определяются по формуле (2)).

Для анализа чувствительности контрольных карт к нарушениям процесса, как отмечалось, необходимо проведение статистических испытаний. С этой целью надо иметь множество аналогичных выборок (с вектором средних и ковариационной матрицей, соответствующими

обучающей выборке, полученной в реальном процессе): объективная оценка средней длины серий возможна лишь по множеству выборок.

Испытания повторяют N раз. Обычно N = 100 ... 1000 - количество смоделированных выборок; оценивается в зависимости от необходимой точности; длина серий оценивается с точностью до одной выборки.

Качество смоделированных выборок может быть оценено по соответствию вектора математических ожиданий и ковариационной матрицы исходным характеристикам для обучающей выборки. Для проверки гипотезы о равенстве векторов средних значений H 0 : ц 1 = ц ₂ при объемах сравниваемых выборок соответственно n 1 и n ₂ может быть использована статистика Хотел -линга, а для проверки гипотезы о равенстве ковариационных матриц Н 0 : S 1 = S ₂ используется специальный критерий [9].

Для оценивания средней длины серий при различных вариантах контроля необходимо смоделировать возможные нарушения процесса. Наиболее распространенным нарушением является увеличение рассеяния вибраций по одному или нескольким параметрам на некоторое постоянное значение, также возможно постепенное увеличение рассеяния (тренд).

Для смоделированных данных строятся карты обобщенной дисперсии, по которым и находится длина серий для данного нарушения. Усредняя результат по множеству выборок, получим среднюю длину серий. Полученный результат полезно сравнить с результатами теоретического расчета: в предположении нормальности распределения обобщенной дисперсии ее средняя длина серий может быть найдена

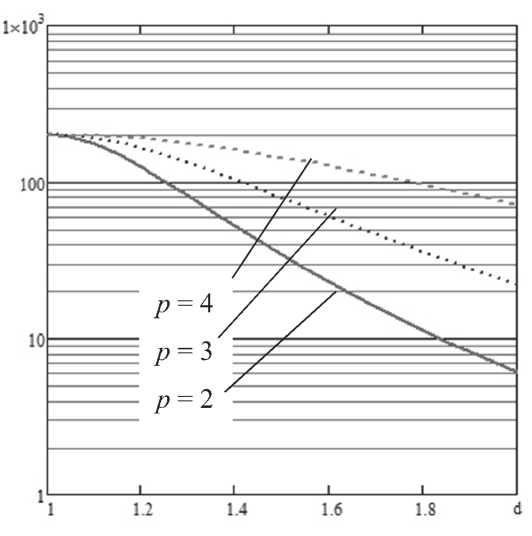
Рис. 1. Кривые средней длины серий для карты обобщенной дисперсии

аналитически. На рис. 1 показаны соответствующие кривые (в полулогарифмических координатах) при количестве контролируемых показателей вибраций р , построенные в системе Mathcad. Из рис. 1 следует, например, что для обнаружения увеличения обобщенной дисперсии в d = 1,5 раза при контроле двух показателей потребуется в среднем 34 выборки.

Если найденная средняя длина серий не удовлетворяет предъявляемым требованиям по своевременности обнаружения нарушения стабильности вибраций, возможно применение специальных мер. Это или увеличение объема мгновенных выборок при контроле, или анализ неслучайных структур на карте обобщенной дисперсии, применение предупреждающей границы, расчете кумулятивных сумм или экспоненциально взвешенных скользящих средних по обобщенной дисперсии.