Оценка статических потерь мощности в квазирезонансном преобразователе напряжения

Одним из перспективных направлений в развитии импульсных преобразователей электроэнергии является применение резонансных контуров (РК) в цепи электронных ключей, которое позволяет распределить энергию между элементами РК внутри одного цикла коммутации и за счет этого осуществлять переключение при нулевом значении тока или напряжения, что позволяет повысить КПД и удельную мощность преобразователя. Под влиянием элементов РК форма тока и напряжения становится близкой к синусоидальной, благодаря чему снижаются потери на высших гармониках в магнитных компонентах фильтров и трансформаторов, а также уровень коммутационных помех [1; 2].

Однако несмотря на все достоинства резонансных и квазирезонансных преобразователей по сравнению с классическими импульсными преобразователями напряжения (ПН) с прямоугольной формой сигналов в силовой цепи и широтно-импульсной модуляцией (ШИМ) пиковые значения тока и напряжения в резонансном цикле могут существенно превышать аналогичные показатели традиционных ПН, что в свою очередь повышает требования к предельным характеристикам полупроводниковых силовых компонентов. Если принять во внимание частотно-импульсный закон регулирования в ПН резонансного типа и зависимость эффективного тока, протекающего через полупроводниковые компоненты силовой части ПН от текущего режима (входных и входных тока и напряжения) и параметров РК, то в заданном диапазоне регулирования выходной величины ПН можно подобрать такие параметры, при которых статические потери будут минимальными.

Проведем сравнительный анализ статических потерь в полупроводниковых ключах традиционного ПН с ШИМ и квазирезонансного ПН с переключением ключевого элемента (КЭ) при нулевых значениях тока (ПНТ) (рис. 1).

Возможны два режима ПНТ [3] (рис. 2): в режиме ПНТ-1 используется половина волны тока резонансного цикла (рис. 2, а), в режиме ПНТ-2 – полная волна тока резонансного цикла (рис. 2, б). Режим ПНТ-1 реализуется в ПН, схема которого приведена на рис . 1. Для режима ПНТ-2 из этой схемы необходимо исключить диод VD1, чтобы обеспечить протекание тока в обратном направлении через обратный диод, шунтирующий МДП-транзистор.

Рис. 1. Схема силовой части ПН с ПНТ:

U вх – входное напряжение; VT 1 – МДП-ключ; L р и С р – индуктивность и емкость РК; L ф и C ф – индуктивность и емкость выходного фильтра; R н – сопротивление нагрузки

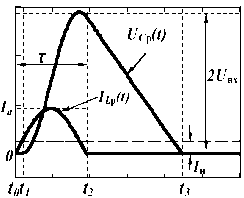
а

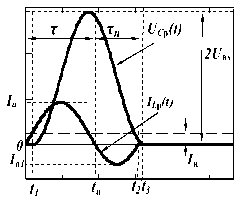
б

Рис. 2. Идеализированные сигналы в цепи РК ПН с режимами ПНТ-1 ( а ) и ПНТ-2 ( б )

Каждый резонансный цикл работы ПНТ-преобразователя можно условно разбить на четыре временных интервала, функции тока и напряжения РК для которых описываются уравнениями, приведенными в табл. 1, при допущении, что ток дросселя выходного фильтра является постоянной величиной, равной току нагрузки в установившемся режиме I н [4].

Оценим статические потери в коммутирующих транзисторных и диодных элементах путем их сравнения с аналогичными потерями в классическом ПН с ШИМ с такой же топологией и жестким переключением КЭ при прочих равных условиях: входном и выходном напряжениях, токе нагрузки, используемой элементной базе.

Таблица 1

Интервал времени	ПНТ-1	ПНТ-2
0 <  t <  ti	kp ( t ) = ( U вх / L p ) t , UC р ( t ) = 0, I vd ( t )	= I н - ( U вх / L p ) t , А t i = t i = I н L p / U вх
t 1 < t <  t 2	kp ( t ) = I н + Z 01 U вх sin ( “ 0 ( t - t i ) ) , U Cp ( t ) = U вх ( l-cos ( “ 0 ( t - t i ) ) ) , А 1 2 = 1 2 - t i = ® 01 [* + arcsin ( Z 0 1 н / U вх ) ]	I L p ( t ) = I н + Z 0 - i U вх sin ( “ 0 ( t - t i ) ) , UCp ( t ) = U вх ( i - cos ( “ 0 ( t - t i ) ) ) , А 1 2 = 1 2 - t i = ® 0 i [ 2 n - arcsin ( I н Z 0 / U вх ) ]
t 2 <  t <  t 3	UCp ( t ) = - ( t - t 2 ) I н Cp 1 + U вх ( 1 - cos ( ® 0 ( t 2 - t i ) ) ) , IL p ( t ) = 0, А t 3 = t 3 - t 2 = I н C pU вх ( 1 - cos ( ® 0 ( t 2 - t i ) ) )	U c p ( t ) = U вх [ i - T - ( Z 0 1 н / U вх ) 2 ] - I н C p 1 ( t - 1 2 ) , IL p ( t ) = 0, А 1 3 = 1 3 - 1 2 = ( I н Z 0 “ 0 )- i U вх [ i - T - ( Z 0 1 н / U вх ) 2 ]

Примечание . В таблице использованы следующие обозначения: Z ₀ = ( L_р / С_р )^0,5 – волновое сопротивление РК; ω₀ = ( L_рС_р )^–0,5 – собственная частота РК.

При этом будем считать, что основную часть потерь мощности составляют потери на КЭ, которые в свою очередь существенно зависят от режима (ПНТ-1 или ПНТ-2), параметров РК и типов полупроводниковых ключей. Отсюда задачу анализа можно свести к поиску значения соотношения PКЭ ПНТ /PКЭ ШИМ для интересующего нас диапазона нагрузок и входных напряжений, где PКЭ ШИМ – статическая мощность, рассеиваемая на КЭ в открытом состоянии в режиме

ШИМ; PКЭ ПНТ – мощность, рассеиваемая на КЭ в открытом состоянии в режиме ПНТ. Тогда это отно- шение будет выглядеть следующим образом:

T p          J Uо ( t ) ' IШИМ (t ) dt

P КЭ ШИМ  0

P>                            ,

КЭПНТ    J Uо (t) ■ IПНТ (t)dt где Uо(t) и I(t) – напряжение на КЭ в открытом состоянии и ток, протекающий через КЭ, соответственно; T – период преобразования. В случае использования в качестве ключа МДП-транзистора искомое соотношение находится так:

P КЭ ШИМ

P КЭ ПНТ

R о ( I эф ШИМ )

R о ( I эфПНТ )

I эф ШИМ ч Iэф ПНТ ,

,

где y = т/T ~ Uвых / Uвх, здесь т - длительность открытого состояния КЭ, Ia ≈ Iн – амплитудное значение тока через МДП-ключ. Такое приближение возможно при AILф < 2Iн в установившемся режиме, где AIдф -размах пульсаций тока дросселя выходного фильтра; Iн - ток нагрузки. Так, например, для А/Lф /Iн = 1 от- ношение среднеквадратичных значений тока между строго прямоугольной и реальной формой импульса при γ = 0,5 равно 1,041.

Для определения эффективного значения тока КЭ в режиме ПНТ можно исходить из предположения, что положительная полуволна тока соответствует полуволне синусоиды с такой же амплитудой, по крайней мере при 0,75 > IнZ0 /Uвх, учитывая необходимое условие выполнения режима ПНТ 0 < Iн Z0/ Uвх < 1 [2; 4]. Тогда упрощенное выражение, описывающее форму тока КЭ для режима ПНТ-1 и положительной полуволны тока для режима ПНТ-2, можно записать в виде

[(Iн + Uвх / Z0 ) sin (tП / Т) ,0 < t < Т, h (t) = 1              ,                            (4)

^{L p}      [ о, t _и <  t <  f T.

Основные расчетные соотношения по определению эффективного значения тока КЭ для обоих режимов ПНТ представлены в табл. 2.

Далее введем параметр, показывающий отношение эффективного значения тока КЭ в режиме ШИМ к эффективному значению тока исследуемых резо- где Rо – сопротивление открытого канала МДП-тран-зистора; Iэф – эффективное значение тока, протекающего через устройство. Таким образом, для оценки отношения статических потерь достаточно знать соотношение эффективных значений токов.

В общем случае эффективное значение тока произвольной формы для периодического сигнала соответствует его среднеквадратичному значению [5].

Для ПН с ШИМ при условии, что форма тока имеет строго прямоугольную форму, эффективное значение этого тока может быть определено как

нансных режимов при прочих равных условиях, определив этот параметр как функцию от тока нагрузки:

M отн КЭ ^{( I} н ) =

I эф ШИМ ( I н ) I эф ПНТ ( I н )

Используя (3) и (4), получим

M отн КЭ ( I н )

®

I эф ШИМ

= I а Ту ,

I a2 Y

T ₂

f . J [ A ( t ) ] dt

I н        / ² K ( ^I н )

( I н + U вх / Z 0 W f о -т ( I н ) ,

где K ( I н ) – коэффициент, рассчитанный в соответствии с (5).

Таблица 2

Параметр	ПНТ-1	ПНТ-2
I эф	I эф = I aV0,5 T / T
I a	I a = I н + U вх / Z 0
I a 1	–	I a 1 = I н - U вх / Z 0
τ	T = LI / U x + (п + arcsin ( I„Z 0 / U„ xУ^Юп1 р нвх            н0 вх 0
τ n	–	( п - 2arcsin ( I н Z 0 / U вх ) ) ®0 1
T	U Bx K , ( IH ) T 1 н U вых f 0	T _ U вх K 2 ( I н ) to U вх U вых f 0     U вых f 0
J ( I н )	J ( I н ) = I н Z 0 / U вх
K U	U c р / U вх = ( f к / f 1 ) K 1 ( I н )	U c р / U вх = ( f к / f 1 ) K 2 ( I н ) “ f к / f )

Примечание. В таблице использованы следующие обозначения: Iэф – эффективное значение тока КЭ для режимов ПНТ-1 и ПНТ-2; UCр – усредненное по времени значение напряжения на конденсаторе РК, равное выходному напряжению в уста- новившемся режиме при условии идеальности выходного фильтра; KU – коэффициент передачи по напряжению, где K1(Iн) и K2(Iн) – коэффициенты, зависящие от тока нагрузки Iн для режимов ПНТ-1 и ПНТ-2 соответственно:

K 1 ( I н ) = 1 [ п + 0,5 J ( I н ) + arcsin ( J ( I н ) ) +f 1 + j 1 - ( J ( I н ) ) 2 I J ( I н ) ^{- 1} 2 п                                  V                  V _

<

K 2( Iн) = — [2п + 0,5 J (Iн) - arcsin (J (Iн))+[ 1 - ^1 -(J (I н)) IJ (Iн )-1 2п                              V               V fк – частота коммутации; f0 = ω0, параметры Ia, Ia1 , τ, τn определены на рис. 2

С учетом того, что режимы ПНТ-1 и ПНТ-2 имеют граничное условие по максимальному току нагрузки при прочих фиксированных параметрах I н Z 0 / U вх = 1 [3], определим теоретический предел функции (6) для обоих режимов ПНТ:

лее высоких значениях нагрузки, т. е. при отношении I н Z 0 / U вх , близкому к единице, расхождение графиков становится заметным. Таким образом, уточненный теоретический предел исходного отношения (8) будет равен 0,813.

I эф ШИМ ( I н )

I эф ПНТ ( I н )

I н Z 0 = 1

U вх

« 0,737.

Отношение между эффективными значениями тока через открытый канал МДП-ключа для режимов ПНТ и ШИМ в зависимости от тока нагрузки при параметрах, указанных в табл. 3, можно представить в виде соответствующих кривых (рис. 3). Для режима ПНТ-2 отрицательная полуволна тока течет через диод, шунтирующий МДП-ключ, поэтому отношение между эффективными значениями токов через шунтирующий диод и КЭ в режиме ШИМ определяется отдельно по формуле

I эф ШИМ ( I н )

M отн КЭ ( I _H ) = ф--------- *

отн КЭ н

I эф ПНТ* ( I н )

I н ТУ

( - 1 н + U вх / Z 0 )

I п- 2arcsin ( Z 0 1 н / U вх )

V     ^{4 п} U вх / U вых

Кривые на рис. 3 получены численным методом с использованием функции (6) (пунктирные линии) и функции (7) (сплошные линии). Следует отметить, что в рабочем диапазоне I н ≤ U вых / Z 0 , где U вых / Z 0 = I max , функция (7), при выводе которой использован ряд приближений, дает высокое совпадение с точным значением на большей части графика, однако при бо-

Таблица 3

Параметр	L р	C р	L ф	C ф	U вых
Значение	1,04 мкГн	22 нФ	45 мкГн	20 мкФ	24 В

Параметр, показывающий отношение между эф-ф е ктивными значениями тока через рекуперативный диод I_{D эф} для режимов ШИМ и ПНТ в зависимости от тока нагрузки при разных значениях коэффициента передачи в установившемся режиме (рис. 4), определим с помощью следующей формулы:

I D ШИМ ( I н )

Mотн VD( Iн ) = "Тф— =

I D _эф ПНТ ( I н )

_        1.2(1 -T)

T                     2

1 f к J [ I D эф ПНТ ⁽ t ) ] dt

Анализ графиков, приведенных на рис. 4, показывает, что статические потери на рекуперативном диоде для режимов ПНТ-1, ПНТ-2 и ШИМ имеют близкие значения при прочих равных условиях. Это объясняется тем, что форма тока во всех случаях имеет схожий характер. Таким образом, для обоих режимов ПНТ можно ввести следующее допущение:

( t 3 – t ₁) f _к ≈ U _вых/ U _вх.

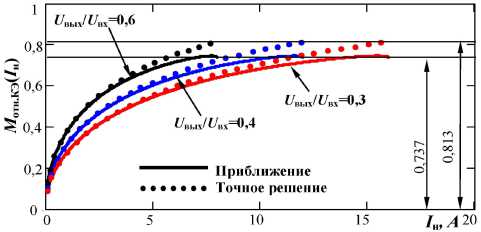
а

Рис. 3. Кривые зависимости M _{отн КЭ}( I _н) для режимов ПНТ-1 ( а ) и ПНТ-2 ( б )

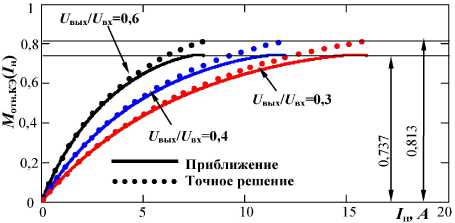
б

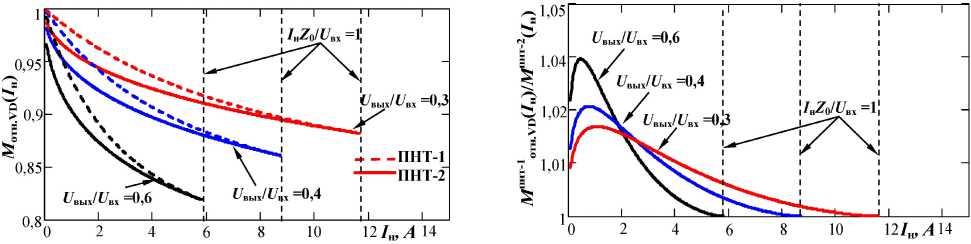
Рис. 4. Зависимость отношения эффективных значений токов, протекающих через рекуперативный диод, для режимов ПНТ ( а ) и ШИМ ( б )

На основании полученных выше результатов можно сделать два вывода:

– статические потери на КЭ в обоих режимах ПНТ выше аналогичных потерь в традиционном ПН с ШИМ при прочих равных условиях, а их отношение M отн имеет предел, который не зависит от параметров РК, коэффициента передачи, тока нагрузки и типа режима ПНТ;

– статические потери на КЭ для двух режимов ПНТ будут тем ближе к аналогичным потерям в классическом ПН при прочих равных условиях, чем I н Z 0 / U вх будет ближе к единице. Однако в реальных условиях невозможно обеспечить выполнение даже приближенного равенства I н Z 0 / U вх ≈ 1, так как ПН постоянного тока обычно применяются в условиях изменения напряжения первичного источника электропитания и тока нагрузки. В свою очередь выходное напряжение остается стабильным за счет замкнутого регулирования выходной величины, при этом требования к отклонению выходной величины могут быть от единиц до сотых долей процента.

Таким образом, дальнейший анализ будет сводиться к сравнению статических потерь на КЭ между исследуемыми типами ПН в широком диапазоне регулирования, т. е. к оценке разницы между статическими потерями КЭ при максимальном и минимальном входном напряжении и фиксированном значении тока нагрузки Iconst и при максимальном и минимальном выходном токе и фиксированном значении вход- ного напряжения Uconst. В этом случае максимальное значение тока нагрузки будет Imax = Uconst /Z0.

Произведем замену аргумента в функции J ( I н )

( см . табл. 1) на I max :

J = J ( U ax) = -0" • -const" = -con st/ — x, (11) max                         const вх

U _вх Z ₀

где 0 <  J ^*< 1.

При фиксированном значении входного напряжения U вх и меняющемся токе нагрузки I н в качестве аргумента функции (11) можно использовать минимальное входное напряжение U min = I const / Z 0 :

Z

J = J ( U _min) = —^ • -н- = I _H / I _const.     (12)

min                      н const

I const Z 0

Таким образом, разница между J ^* и J состоит в том, что J ^* вычисляется при фиксированном токе нагрузки или при фиксированном входном напряжении.

Функция (7) с использованием (11) и (12) для режимов ПНТ-1 и ПНТ-2 может быть определена как

*

M max КЭ ПНТ-1 ⁽ J ) =

*, (13)

1 + ( J *) ¹ \n + arcsin( J *) + J

*\        1            4 ^П K ² ( J )

M max КЭ ПНТ-2⁽ J ) = ; TT^T 1       ^"77^  7

1 + ( J ) ¹ n + arcsin( J ) + J

, (14)

где K1(J *) и K2(J *) – коэффициенты передачи для обоих режимов ПНТ в соответствии с (5) для аргу- мента J *. Выражения (13) и (14) показывают зависимость эффективных значений токов, проходящих через КЭ, для обоих режимов ПНТ по отношению к эффективному току для режима с ШИМ.

Для того чтобы оценить статические потери при протекании отрицательной полуволны тока через шунтирующий КЭ диод в режиме ПНТ-2, можно вос- пользоваться всеми рассмотренными ранее допущениями и выкладками. Тогда, подставляя (11) или (12) в (9), получим:

M *maXK3( J *) =----~T max КЭ

( J * ) '

-

4 n K 2 ( J * )

1 n — 2arcsin( J * )

.

Таким образом, мы получили формулы (7), (9) в универсальном виде (13)…(15), т. е. без включения внутренних параметров исследуемых ПН, что позволяет сделать некоторые обобщенные оценки по статическим потерям на КЭ для любых условий и параметров в пределах условий реализации режима ПНТ.

Для того чтобы сравнить статические потери на КЭ между режимами ПНТ-1 и ПНТ-2, необходимо найти отношение потерь только на КЭ, так как разни- ца между статическими потерями на рекуперативном диоде для этих режимов несущественна. Тогда отношение статических потерь на КЭ для режимов ПНТ-1 и ПНТ-2 при прочих равных условиях с учетом статических потерь на шунтирующем МДП-ключ диоде для режима ПНТ-2 может быть найдено как

* — 2

M max КЭ ПНТ-1 ( J )

^р отнПНТ                     , .*. — 2 , ,,*        , ,*x — 1 ’ ⁽¹⁶⁾

M max КЭ ПНТ-2⁽ J ) + M max КЭ ⁽ J ) ^X

X U d / ( I a R о Vr )

где U D /( I a R о γ^0,5) – коэффициент, который необходим, чтобы числитель каждого члена выражения был одинаковым, здесь U D – прямое падение напряжения на шунтирующем диоде, I a = I н , γ – коэффициент заполнения для ПН с ШИМ при прочих равных условиях .

Чтобы определить выражение (15) как функцию от J ^* , необходимо найти коэффициент заполнения как функцию от J ^* .

Если выразить уравнение (11) как U вх = U min / J ^* и подставить его в формулу γ = U вых / U вх , то получим γ( J ^* ) = J ^* U вых / U min при фиксированном значении тока нагрузки и условии, что выражение (11) справедливо. А если ввести A 1 = (( U вых / U min )^0,5 I a R о )/ U D , где R о – сопротивление канала МДП-транзистора в открытом состоянии, то уравнение (16) примет вид

D          *        ^M max КЭ ПНТ-1 ⁽ J )

P OTH ПНТ-1⁽ J ) ^-                     , *.-2

M max КЭ ПНТ-2 ⁽ J ) +

.

P OTH ПНТ-2 ⁽ J ) ^-

M max КЭ ПНТ-1⁽ J ) 2

M max КЭ ПНТ-2 ⁽ J ) +

,

*                             *

+ ( M max КЭ ⁽ J ) "  A 2 V J )

где γ = const; A ₂ = ( I _max R _оγ²)/ U_D . Выражение для А ₂ получено подстановкой I н = I a = J ^* I max в U D /( I a R о D ^0,5).

При использовании понижающего ПН с режимом ПНТ-1 необходимо учитывать статические потери на диоде, включенном последовательно с МДП-ключом. Тогда уравнения (17) и (18) примут вид

* — 2

M max КЭ ПНТ-1⁽ J ) +

P OTH ПНТ-1⁽ J ) ^-

+ ( M max КЭ ПНТ-1 ⁽ J ) ' A 1 ^^ )

M max КЭ ПНТ-2 ⁽ J ) +

,

+ ( M max КЭ

- 1

M max КЭ ПНТ-1⁽ J ) +

*

P OTH ПНТ-2 ⁽ J ) ^-

+ ( M max КЭ ПНТ-1 ⁽ J ) ' A 2

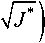
- 1

i r                 / т *\ — 2

M max КЭ ПНТ-2⁽ J ) +

.

i                                       I -----\ — 1

***

+ ( M max КЭ ⁽ J ) ' A 2^ J )

Если шунтирующий диод для режима ПНТ-2 и последовательный диод для режима ПНТ-1 различны, то коэффициент А необходимо пересчитать отдельно для числителя и знаменателя функций (19) и (20).

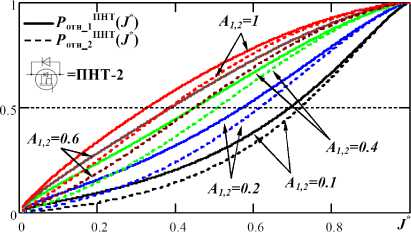
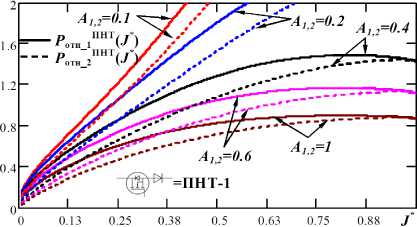
Совокупность кривых при разных значениях коэффициента А для функций (17), (18) и (19), (20) приведена ниже (рис. 5).

Все представленные выше вычисления приводились при допущении, что А/Lф << 21н в установив- шемся режиме, при этом точность предложенного метода сравнительной оценки будет снижаться с приближением соотношения 0,5^ А/^^ /1н к единице.

Для сравнения режимов ПНТ-1 и ПНТ-2 по статическим потерям мощности необходимо, чтобы другие виды потерь в двух сравниваемых ПН имели одну и ту же природу при прочих равных условиях. Как показали экспериментальные исследования, в режиме ПНТ-2 следствием протекания отрицательной полуволны тока через встроенный в МДП-ключ диод является процесс его обратного восстановления, что приводит к возникновению дополнительных динамических потерь. Типовым решением для устранения этого процесса является шунтирование МДП-ключа диодом с барьером Шоттки, рассчитанным на такое же блокирующее напряжение, что и МДП-ключ. Эксперимент, в котором были использованы МДП-ключ и диод Шоттки с блокирующим напряжением 150 В, показал, что полностью устранить процесс обратного восстановления встроенного диода не удается.

В ходе эксперимента были получены кривые КПД для разных вариантов КЭ (рис. 6) для обоих режимов ПНТ с параметрами элементов, представленными в табл. 3, при изменении J ^* (рис. 7).

а

б

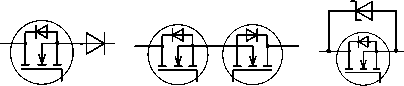
а                    б                  в

Рис. 6. Варианты КЭ на основе МДП-транзисторов для режимов ПНТ-1 ( а , б ) и ПНТ-2 ( в , г , д )

Рис. 5. Теоретические кривые отношения статических потерь на КЭ между режимами ПНТ-1 и ПНТ-2: а – для функций (17) и (18); б – для функций (19) и (20)

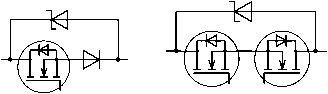
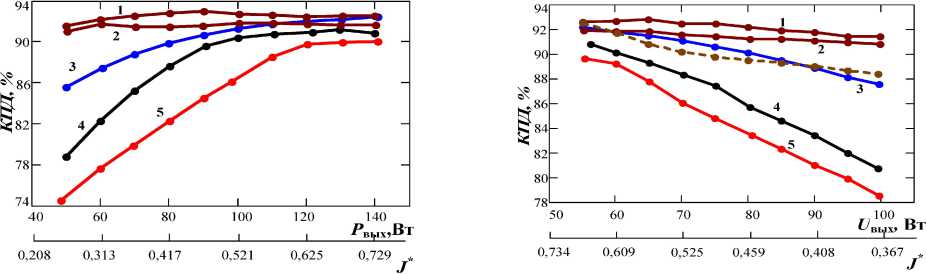
б

Рис. 7. Кривые КПД ПН с ПНТ с разными вариантами КЭ:

а – при фиксированном входном напряжении U вх = 55 В; б – фиксированном выходном токе I н = 5,34 А (пунктиром показана кривая КПД снятая для традиционного последовательного ПН с ШИМ с частотой коммутации 470 КГц)

Кривые 1 и 2 построены для режима ПНТ-1 с КЭ, приведенными на рис. 6, а и б соответственно, кривая 3 – для режима ПНТ-2 с КЭ с шунтирующим диодом Шоттки (рис. 6, д ), кривые 4 и 5 – для режима ПНТ-2 с КЭ, приведенным на рис. 6, в , и КЭ в виде одного МДП-ключа (рис. 6, г ). Максимальная частота коммутации составила 500 КГц при минимальном входном напряжении и максимальной выходной мощности для обоих режимов ПНТ. В эксперименте использовались диоды Шоттки 10CTQ150 и МДП-транзисторы IRFB61N15D.

Кривые 3, 4 и 5 показывают, что введение диода Шоттки ослабляет процесс обратного восстановления встроенного диода МДП-ключа, но не исключает его полностью. При возрастании параметра J * значения кривых КПД становятся близкими друг к другу, особенно кривых 1 и 3, различие между которыми определяется только статическими потерями КЭ. Ранее было отмечено, что чем ближе J * к единице, тем меньше разница в статических потерях между режимами ПНТ-1 и ПНТ-2, и эта разница в идеальном случае, т. е. при идентичности всех элементов, будет равна нулю при J * = 1. Таким образом, наиболее привлекательным типом КЭ для режима ПНТ-1 является КЭ на рис. 6, б, а для режима ПНТ-2 – КЭ на рис. 6, д.

В заключении представим теоретические и экспериментальные кривые, определяемые выражениями (19), (20), которые были построены для фиксированного входного напряжения U вх = 55 В и фиксированного выходного тока I н = 5,34 А (рис. 8).

Рис. 8. Теоретические и экспериментальные кривые, полученные по выражениям (19), (20), для фиксированного входного напряжения U _вх = 55 В и фиксированного выходного тока I _н = 5,34 А

Экспериментальные кривые были получены для КЭ, изображенных на рис. 6, б и д , для режимов ПНТ-1 и ПНТ-2 соответственно.

Экспериментальные кривые на рис. 8 близки к теоретическим во всем диапазоне измерений, что подтверждает предложенный в данной статье подход к сравнительной оценке статических потерь, который позволяет оценивать разницу статических потерь на КЭ между режимами ПНТ-1 и ПНТ-2 при различных условиях, определяемых одним показателем А. Необходимо также отметить, что КЭ для каждого из исследуемых режимов ПНТ различаются (см. рис. 6), и если исключить процесс обратного восстановления встроенного в МДП-ключ диода в режиме ПНТ-2, то его КПД может быть выше, чем КПД диода в режиме ПНТ-1 для диапазона m <  J ^*< 1, где m – значение J ^* при P отн ПНТ = 1 (см. рис. 5).

В данной статье предложен метод сравнительной оценки статических потерь мощности на КЭ традиционного ПН с ШИМ и последовательного квазирезо-нансного ПН с переключением при нулевых значениях тока, который показал, что:

• –    статические потери КЭ в ПН с ПНТ больше, чем в традиционном ПН с ШИМ, а их отношение имеет предел, который не зависит от параметров РК;

• –    в случае когда входное и выходное напряжения и ток нагрузки проектируемого ПН стабильны или изменяются незначительно, параметры РК должны быть подобраны таким образом, чтобы обеспечить параметр J близким к единице, при этом достигается минимум статических потерь на КЭ;

  – если диапазон регулирования существенный, т. е. когда параметр J ^* изменяется более чем на 10 %, то статические потери на КЭ для режима ПНТ-2 могут быть значительно больше по сравнению с режимом ПНТ-1 при идентичных КЭ. С другой стороны,

в режиме ПНТ-1 диапазон изменения частоты определяется как диапазоном токов нагрузки, так и входным напряжением.

Таким образом, квазирезонансный ПН с частотноимпульсной модуляцией, работающий в режимах ПНТ-1 и ПНТ-2, может иметь преимущество по КПД и удельной мощности в широком диапазоне регулирования по сравнению с традиционным ПН с ШИМ при прочих равных условиях, когда динамические потери КЭ при жестком режиме переключения будут больше, чем статические потери в режиме ПНТ при минимальном возможном параметре J ^* и минимальной частоте преобразования.

Представленный метод может быть полезен при проектировании импульсного высокочастотного стабилизированного источника питания, когда возникает необходимость в выборе типа преобразователя напряжения между традиционным ПМ с ШИМ и ПН с режимом ПНТ-1 или ПНТ-2.