Оценка стоимости опционов

студент 5 курса

Научный руководитель - Пихтарева А.В.

ассистент кафедра «Финансы и кредит»

Поволжский государственный университет сервиса

Россия, г. Тольятти ОЦЕНКА СТОИМОСТИ ОПЦИОНОВ

В 1973 году в Чикаго была основана опционная биржа. Она имела почти постоянный успех. В течение пяти лет инвесторы заключали опционные сделки на покупку или продажу более 10 млн. акций ежедневно.

Сегодня опционами торгуют на многих биржах. Кроме срочных сделок на покупку или продажу обыкновенных акций заключаются опционные контракты на фондовые индексы, на облигации, товары и иностранную валюту. Существуют различные стратегии и модели оценки опционных сделок.

Опционный контракт – предоставляет держателю право принять или осуществить поставку базисного актива по заранее установленной цене.

Контракт, предоставляющий своему покупателю право:

• •    купить базовый актив по установленной цене не позднее установленной даты называется опцион «колл»;

  
  
  

• •    продать базовый актив по установленной цене не позднее установленной даты называется опцион «пут».

Существуют различные стратегии, которые позволяют отразить выигрыши и потери как покупателя, так и продавца опционов. Рассмотрим основные варианты.

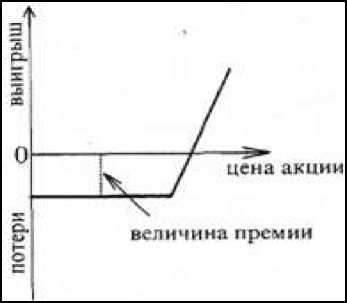
Покупка опциона «колл» представлена на рис. 1.

Формула расчета выигрыша (потери):

Ра — рыночная цена акции;

Е — цена исполнения опциона;

П — премия;

R — результат (выигрыш или потери):

При Ра> Е, R = [Ра-(E + R)];

При Ра < E, R = - П

Рис.1 Покупка опциона «колл»

Данная стратегия используется при росте цен на рынке, при этом доход неограничен, а минимальный риск — величина уплаченной прибыли. Потенциальная прибыль владельца опциона в целом включает в себя стоимость ценной бумаги на момент истечения срока действия опциона минус цена исполнения и минус выплаченная премия.

На рис. 2 представлена продажа опциона «колл».

Формула расчета выигрыша (потери) соответствует покупке опциона

«колл», но со знаком минус:

при Ра >E, R = (E + П) - Ра =[ Ра - (E + П)];

при Ра < E, R = П.

Представленная стратегия используется, когда на рынке цены имеют тенденцию к снижению. Максимальный доход составит величина полученной премии, при этом максимальный риск неограничен.

Рис.2. Продажа опциона «колл»

Рис.3 демонстрирует покупку опциона «пут» (Рис. 3). Эта стратегия используется при снижении цен на рынке. Максимальный доход равен цене исполнения минус премия.

Формула расчета выигрыша (потери):

при Ра > E, R = - П;

при Ра < E, R = (E - П) - Ра.

Рис.3. Покупка опциона «пут»

Продажа опциона «пут» изображена на

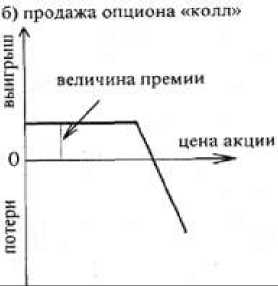
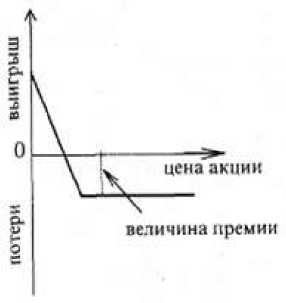
рис.4.

Формула расчета выигрыша (потери) соответствует покупке опциона

«пут», но со знаком минус:

при Р а ≥ Е, R = + П;

при Р а < E, R = Р а - (Е - П) = - [(Е - П) - Р а ].

Данная стратегия предполагает, что курс ценной бумаги не упадет, а, следовательно, опцион останется относительно стабильным. Максимальный доход — это полученная премия. Максимальный риск — это цена исполнения минус премия.

Рис.4. Продажа опциона «пут»

Сравним указанные выше результаты по всем видам базисных опционных стратегий (табл. 1).

Таблица 1

Результаты осуществления базисных опционных стратегий

Вилы стратегий	При Р.>Е	R	При P.< E	R
1. Покупка опциона «колл»	R = P.-(E + nj	Ri	Н=-П	R:
2. Продажа опциона «колл»	R= fP. - fE + Hi}	R:	R- +11	Ri
3. Покупка опциона «пут»	R = - 11	R,	R = /E-H)_ p„	R:
4. Продажа опциона «пут»	R = + H	R:	R = (E Ui Pt	Ri

Как следует из данных таблицы 1, пары стратегий: покупка и продажа опционов «колл» и покупка и продажа опционов «пут» имеют одинаковые результаты по абсолютной величине, но противоположные по знаку. Кроме того, если учесть, что R 1 = Р а - (Е + П) и R 2 = - П, то R 1 – R 2 = Р а - Е, и следовательно, R 2 = R 1 + (Е - Р а ).

В итоге получается, что если известен результат по опциону «колл» ( R 1 или R 2 , где R 1 — прибыль, a R 2 — убыток), то результат по опциону «пут» с той же ценой исполнения (Е) и датой исполнения отличается от первого лишь на величину разности между ценой исполнения опциона (Е) и рыночной ценой актива (Ра).

Ожидаемые результаты от вида стратегий представлены в таблице 2.

Таблица 2

Результаты сделок базисных опционных стратегий

Сторона сделки	Соотношение цены актива и цены исполнения опциона	Результат
		опцион на покупку	опцион на продажу
Покупатель опциона	Л^Е	Л,
	Ра<Е	к?	к.
Продавец опциона	№	Л/	R:
	< Е	Л.	К,

Где: Ра— цена актива, лежащего в основе опциона в момент его исполнения; Е — цена исполнения опциона; R 1,2 — результат (прибыль или убыток) опциона в зависимости от соотношения цены актива и цены исполнения опциона.

Наиболее интересные стратегии формируются за счет различных комбинаций и спрэдов. Рассмотрим одну из них.

Стеллажная сделка стрэддл (straddle) представляет собой комбинацию опционов «колл» и «пут» на одни и те же акции с одинаковой ценой исполнения и сроком истечения контрактов (рис. 5 и рис.6).

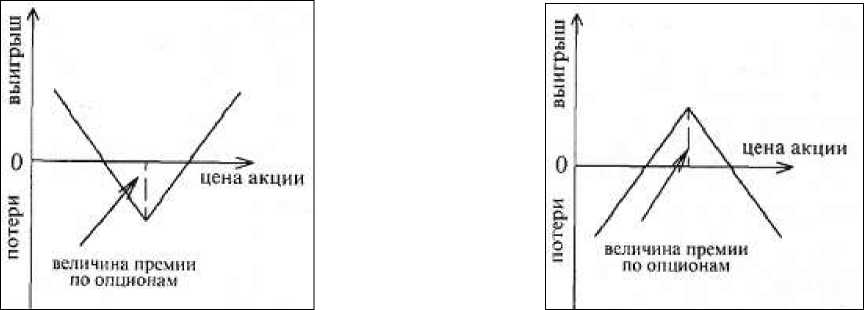
Рис.6. Продажа

Рис.5. Покупка опционов «пут» и опционов «пут» и

«колл» (стеллаж)                                        «колл»

(стеллаж)

Покупатель платит по данной сделке две премии. Если премия по опционам различается существенным образом, то такая ситуация называется искусственным стеллажом.

Для расчета выигрыша (потерь) покупателя стеллажа можно использовать следующую формулу расчета:

При Р а ≥ Е, R = (Р а – E) – (П 1 + П 2 )

При Р а < E, R = (E - Р а ) - (П 1 + П 2 )

где Ра — цена акции; Е — цена исполнения опционов; П 1 — премия опциона «колл»; П 2 — премия опциона «пут»; R — результат (выигрыш или потери).

Максимальный риск, который может понести инвестор, используя данную стратегию, — это сумма уплаченных премий, а доход при этом неограничен.

Если цена акции составляет 30 руб. и инвестор приобретает стеллаж с ценой исполнения 31 руб. и сроком истечения контракта через три месяца, ожидая значительного изменения курса акций, то премия опционов «колл» и «пут» составляет по 3 руб. каждая.

К моменту истечения контрактов на рынке возможны следующие ситуации:

• а)    цена акций поднялась до 31 руб. В этом случае опционы не исполняются и инвестор несет потери в размере 6 руб. с каждой акции;

• б)    цена акции повысилась до 37 руб. Инвестор исполняет опцион «колл» и получит доход, равный 37 руб. —31 руб. = 6 руб. Однако в качестве премии он уже уплатил 6 дол. продавцу стеллажа, поэтому общий итог по сделке равен 0;

• в)    цена акции достигла 40 руб. Инвестор исполняет опцион «колл» и получит прибыль в размере: 40 руб. — 31 руб. — 6 руб. = 3 руб.;

• г)    цена акции опустилась до 25 руб. Инвестор исполняет опцион «пут». Однако его доход полностью компенсируется уплаченной за стеллаж премией и поэтому 31 руб. — 25 руб. — 6 руб. = 0;

• д)    цена акции достигла 20 руб. Инвестор исполняет опцион «пут» и получает прибыль, равную: 31 руб. — 20 руб. — 6 руб. = 5 руб.

Таким образом, инвестор получит прибыль по сделке, если курс акций будет выше 37 руб. или ниже 25 руб. При курсе, равном 37 руб. или 25 руб., инвестор завершит сделку с нулевым результатом. Если курс будет больше 25 руб., но меньше 37 руб., покупатель стеллажа несет потери. Их максимальный размер при курсе, равном 37 руб., составит 6 руб. При отклонении стоимости ценной бумаги от этого уровня вверх или вниз инвестор исполнит один из опционов, чтобы уменьшить свои потери. Например, если курс составляет 33 руб., то покупатель исполняет опцион «колл», сокращая свои потери до уровня равного:

6 руб. - 33 руб. + 31 руб. = 4 руб.

Если курс понизился до 28 руб., то показатель исполняет опцион «пут» и уменьшает потери до размера:

6 руб. - 31 руб. + 28 руб. = 3 руб.

Продавец стеллажа получит прибыль при условии:

25 руб. < цена акции < 27 руб, то есть тогда, когда цена акции станет равной 26 руб.

Таким образом стеллажные сделки в виде стрэддла отражают комбинацию опционов при занятии инвестора длинной или только короткой позиции. Вкладчик же выбирает данную стратегию, когда ожидает изменения курса акций.

БИНОМИНАЛЬНАЯ МОДЕЛЬ ОЦЕНКИ СТОИМОСТИ ОПЦИОНОВ

Провести оценку стоимости опционов также возможно с помощью биноминальной модели.

Предположим, что цена акции компании сегодня (t = 0) равна 100 руб., а через год (t = Т) эта акция будет стоить 125 руб. или 80 руб., т.е. цена акции за год или поднимется на 25%, или упадет на 20% (рис.7). Кроме того, непрерывно начисляемая ставка без риска в расчете на год равна 8%. Предполагается, что инвесторы могут предоставлять кредит (покупая 8%-ные облигации) и занимать средства (осуществляя продажи облигаций) под данный процент.

Рассмотрим опцион «колл» на акции компании с ценой исполнения 100 руб. и датой истечения через год. Это означает, что на дату истечения стоимость опциона «колл» составит или 25 руб. (если акция стоит 125 руб.),

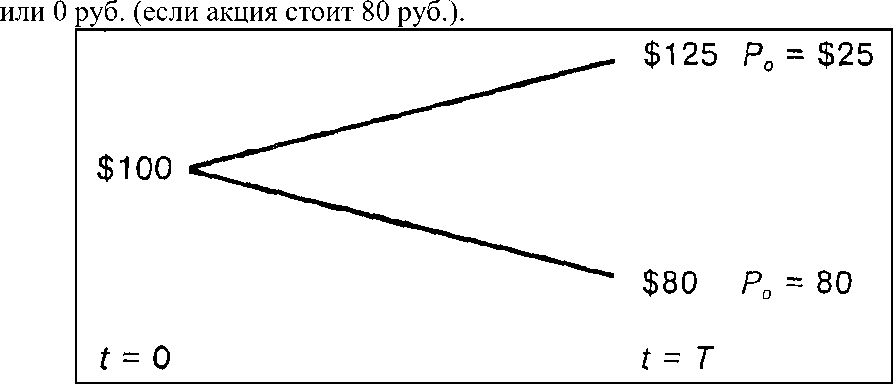
Рис. 7. Биноминальная модель оценки стоимости акций компании

Рассмотрим возможные варианты инвестирования средств в компанию: 1) вложение средства в акцию, 2) опцион и 3) облигацию без риска. Цены и результаты операции с акцией известны. Также известно, что 100 руб. инвестируются в безрисковую облигацию, стоимость которой вырастет приблизительно до 108,33 руб. с учетом непрерывно начисляемого процента (по формуле сложных процентов), равного 8% годовых.

При известных результатах опционной операции в конце периода определим цену продажи опциона в настоящий момент. Возможны два варианта развития ситуации в будущем, когда курс акции может пойти как вверх так и вниз (табл.3).

Таблица 3.

Цены и результаты операций с акцией, облигацией и опционом

Ценная бумага	В ьш л аты в «в ерхн ем и сложении »	Выплаты в «нижнем положении»	Текущий курс
Акция	125	80	100
Облигация	10832	10833	100
Опцион «колл»	25	0	7

Определим состав портфеля, который точно повторит выплаты по опциону «колл» на акции компании. Для этого рассмотрим портфель из Ns акций компании и Nb безрисковых облигаций.

В «верхнем положении» такой портфель принесет выплаты в размере 125 Ns + 108,33 Nb, в «нижнем положении» выплаты составят 80Ns + 108,33Nb. В «верхнем положении» опцион стоит 25 руб. Таким образом, Ns и Nb должны иметь такую стоимость, чтобы:

125 Ns + 108,33 Nb = 25

С другой стороны, в «нижнем положении» опцион равен нулю. Таким образом, Ns и Nb должны иметь такую стоимость, чтобы:

80 Ns + 108,33 Nb = 0

(125 - 80) Ns = 25

откуда Ns = 0,5556, Nb = - 0,4103.

Это значит, что инвестор может воспроизвести платежи по опциону «колл», осуществив продажу безрисковой облигации за 41,03 руб. и купив 0,5556 акций компании (табл.4).

Таблица 4.

Затраты инвестора на опцион

Состав портфеля	Выплата в «верхнем положении»	Выплата в «нижнем положении»
Инвестиции в акции	0,5556 х 125=69,45	0,5556 х 80= 44,45
Выплата займа	-41,03 х 1,0833 = -44,45	-41,03 х 1,0833 = -44,45
Чистая выплата	25	0

Таким образом, чтобы сформировать портфель, надо затратить 55,56 руб. на покупку 0,5556 акций компании (по цене 100 руб. за акцию). Кроме того, 41,03 руб. получается от продажи облигации.

В результате требуется только 14,53 руб. (55,56 руб.- 41,03 руб.) собственных средств инвестора. Следовательно, это и есть действительная стоимость опциона «колл».

В общем виде, стоимость опциона «колл» будет равна:

Vo = NsPs + NbPb, где Vo — стоимость опциона,

Ps — цена акции,

Рь — цена безрисковой облигации,

Ns и Nb - число акций и безрисковых облигаций, позволяющих воспроизвести выплаты по опциону.

Подводя итог, следует отметить, что действительные цены опционов «колл» и «пут» позволяют построить их различные стратегии. Все они базируются на цене акции, цене исполнения, премии и в каждом конкретном случае определяют выигрыш или потери инвестора. Сделки с различными опционами создают всевозможные игровые конструкции, которые в свою очередь могут создавать альтернативные подходы к решению одних и тех же задач. Вместе с тем, как показывает зарубежный опыт, накопленная за многие годы статистика далеко не всегда позволяет использовать предыдущий опыт для принятия правильных решений. Поэтому среди разных зарубежных специалистов нет единства в оценках стратегических планов опционной торговли.

Для оценки стоимости опциона «колл» или «пут» может быть использована биноминальная модель стоимости (ВОРМ). Модель построена в предположении, что базисный актив будет равен одной из двух возможных известных цен по истечении каждого из ограниченных числа периодов, а также при условии, что известна цена актива в начале каждого периода.