Оценка технического состояния круглых шестеренных гидронасосов навесных гидросистем тракторов

Автор: Чумаков Павел Васильевич, Мартынов Алексей Владимирович, Коломейченко Александр Викторович, Хасан Исмаил Халил, Коломейченко Алла Сергеевна

Журнал: Инженерные технологии и системы @vestnik-mrsu

Рубрика: Технологии и средства технического обслуживания в сельском хозяйстве

Статья в выпуске: 3, 2020 года.

Бесплатный доступ

Введение. В условиях предприятий технического сервиса достоверная оценка технического состояния гидравлических шестеренных насосов навесных гидросистем тракторов является первоочередной задачей при внедрении в производство новых процессов ремонта. Отсутствие данных заводов-изготовителей о предельных значениях износов рабочих поверхностей деталей гидравлических насосов, при достижении которых принимается решение о ремонте, приводит к необходимости проведения дополнительных исследований. В связи с этим целью работы является поиск предельных значений износов рабочих поверхностей деталей круглых шестеренных гидронасосов. Материалы и методы. Лабораторные стендовые испытания бывших в эксплуатации круглых шестеренных гидронасосов осуществлялись по разработанной в ГНУ ГОСНИТИ Россельхозакадемии методике на гидравлическом стенде КИ-28097М-ГОСНИТИ. Контролируемым параметром при проведении стендовых испытаний является коэффициент подачи насоса. Результаты исследования. В работе представлены результаты лабораторных, стендовых и микрометражных исследований бывших в эксплуатации круглых шестеренных гидронасосов. Получена математическая зависимость (модель) коэффициентов подачи круглых шестеренных гидронасосов от износов рабочих поверхностей их деталей. Методом крутого восхождения по полученной математической модели определены предельные значения износов рабочих поверхностей деталей круглых шестеренных гидронасосов. Обсуждение и заключение. По результатам входного стендового контроля бывших в эксплуатации круглых шестеренных насосов установлено, что 81 % исследуемых агрегатов эксплуатировался в запредельном состоянии. Установленные методом крутого восхождения предельные значения износов рабочих поверхностей деталей круглых шестеренных гидронасосов позволяют сделать заключение о необходимости их восстановления при ремонте на предприятиях технического сервиса.

Еще

Гидравлический насос, коэффициент подачи, техническое состояние, износ, микрометраж

Короткий адрес: https://sciup.org/147221967

IDR: 147221967 | DOI: 10.15507/2658-4123.030.202003.426-447

Текст научной статьи Оценка технического состояния круглых шестеренных гидронасосов навесных гидросистем тракторов

Одним из основных агрегатов гидросистемы тракторов является гидравлический насос, который предназначен для преобразования части механиче- ской энергии двигателя внутреннего сгорания трактора в энергию рабочей жидкости. При этом гидронасос способен приводить в движение одновременно несколько конечных элементов

KTSJ гидросистемы (гидроцилиндров), а значит и рабочих органов машины.

Оценочным параметром технического состояния круглых шестеренных гидронасосов является коэффициент подачи η Q . Согласно данным ряда источников коэффициент подачи новых шестеренных гидронасосов составляет 0,95…0,92 [1]. Для навесных гидросистем тракторов, согласно РТМ 70.0001.246-84, предельное значение коэффициента подачи принимается при его падении ниже 60 % от коэффициента подачи новых шестеренных гидронасосов [2].

Согласно данным завода-изготовителя 80-процентный гамма-ресурс круглых шестеренных гидронасосов составляет 6 000 часов [3; 4]. Согласно исследованиям при работе шестеренных насосов в реальных условиях эксплуатации 80-процентный гамма-ресурс составляет 1 800…2 200 часов [5].

Том 30, № 3. 2020

Конструкция круглых шестеренных гидронасосов представлена на рисунке 1.

Согласно устройству круглых шестеренных насосов, представленному на рисунке 1, поверхности под цапфами шестерен поджимной 20 и подшипниковой 12 полуобойм являются наиболее нагруженными узлами.

Износ посадочных мест под цапфы приводит к незначительному повороту поджимной обоймы 20 , в связи с чем происходит нарушение ее прижима к подшипниковой обойме 12 . При этом между наружным диаметром шестерни ведомой 10 и поверхностью обоймы поджимной 20 образуется утечка рабочей гидравлической жидкости [6].

Зазор в сопряжении «поджимная обойма 20 – корпус 1 » значительно снижает работоспособность насоса на холостом ходу. Здесь поджимная

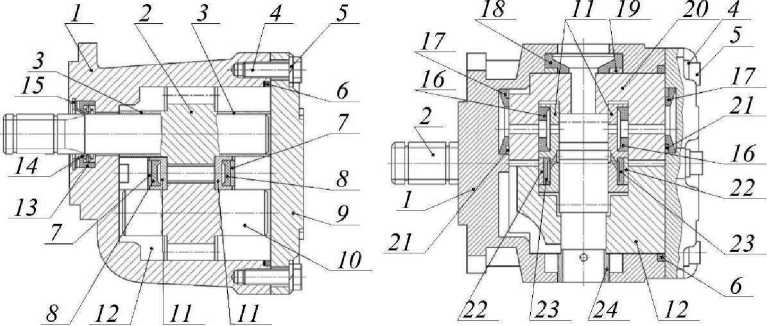
Р и с. 1. Устройство круглого шестеренного насоса: 1 – корпус гидронасоса; 2 – шестерня ведущая; 3 – вкладыши; 4 – винты крепления крышки гидронасоса; 5 – шайбы; 6 – кольцо уплотнительное;

7, 19, 21 и 22 - пластина опорная; 8, 16, 17, 18, 23 - манжета торцевого уплотнения;

9 – крышка насоса; 10 – шестерня ведомая; 11 – платики; 12 – обойма подшипниковая; 13 – манжета ведущей шестерни; 14 – кольцо опорное; 15 – кольцо стопорное; 20 – обойма поджимная;

24 – втулка центрирующая

F i g. 1. Structure of a round gear pump: 1 – hydraulic pump case; 2 – driving gear; 3 – liners;

4 - hydraulic pump cover mounting screws; 5 - washers; 6 - sealing ring;

7, 19, 21 and 22 - support plate; 8, 16, 17, 18, 23 - mechanical seal cuff; 9 - pump cover;

10 - driven gear; 11 - plates; 12 - bearing ring; 13 - driving gear cuff; 14 - support ring;

15 – locking ring; 20 – preload ring; 24 – centering sleeve обойма 20, скользя по манжете 18, поворачивается относительно цапф ведомой 10 и ведущей 2 шестерен. Таким образом увеличивается угол между плоскостями сопряжения обойм. Описанные процессы происходят в связи с возникновением износов рабочих поверхностей деталей, а также релаксационных процессов материала манжеты радиального уплотнения.

С одной стороны, возникновение износов рабочих поверхностей деталей насосов способствует образованию зазора в сопряжении «обойма 20 - корпус 1 », с другой, – возникновению зазора (за счет увеличения межцентрового расстояния) между камерой нагнетания и камерой ведомой и ведущей шестерен.

За счет усилия, создаваемого давлением камеры, обеспечивается герметичное прижатие платиков 11 к торцам ведомой и ведущей шестерен. Выражение для расчета силы поджатия платиков 11 к торцам шестерен 2 , 10 запишется:

^Fm = f l Р нг — f 2 Р щ , (1)

где f l - боковая площадь платика; p _нг -давление нагнетания; f- площадь контакта; p щ – давление в щели уплотнения [7].

Так как f ₂ / f ₁ = 1,2…1,3 = const, то с повышением давления p _нг возрастает усилие прижима F_m [7]. Поэтому в круглых шестеренных насосах с увеличением усилия прижима уменьшается зазор в торцовом уплотнении, которое снижается с увеличением износа рабочих поверхностей деталей.

На основании проведенного анализа можно утверждать, что в период эксплуатации насоса его детали (корпус, шестерни, платики) испытывают напряжения, которые приводят к износам их контактирующих поверхностей, нарушению пространственной геометрии сопряжений и, как следствие, к образованию утечек и снижению объемной подачи агрегата.

В технической документации и технических требованиях на капитальный ремонт круглых шестеренных насосов отсутствуют данные о предельных значениях износов рабочих поверхностей деталей, при достижении которых дальнейшая эксплуатация агрегата не допустима. Однако значения предельных износов рабочих поверхностей деталей круглых гидравлических насосов необходимы для принятия решения об их восстановлении при ремонте. Целью работы является определение предельных значений износов рабочих поверхностей деталей круглых шестеренных гидронасосов.

Обзор литературы

В настоящее время существует множество способов восстановления рабочих поверхностей деталей круглых шестеренных гидронасосов, которые имеют свои преимущества и недостатки [8-10]. Однако потребность восстановления определяется предельными значениями износов деталей [11–14]. В связи с этим необходимо обоснование подхода к определению предельных значений износов рабочих поверхностей деталей круглых шестеренных гидронасосов с учетом наработки и критерия предельного состояния. Критерием предельного состояния круглых шестеренных гидронасосов является снижение коэффициента подачи менее 40 % [2].

По результатам исследования ряда авторов, снижение коэффициента объемной подачи шестеренных гидронасосов подчиняется закону, описываемому формулой [15–18]:

П(t) = П0 - kt1, при П0 > П > Ппр, (2) где η0, ηпр – номинальное (нормативное) и предельное значения коэффициента подачи гидронасоса соответственно; k – величина, характеризующая интенсивность снижения коэффициента подачи; λ – показатель степени, определяющий характер изменения коэффициента подачи. Иллюстрация закона (2) приведена на рисунке 2.

По установленным при входном контроле значениям коэффициента подачи и наработки t_t средний остаточный ресурс шестеренных гидронасосов определяется по формуле [19; 20]:

■ ост

( П 0 ^- П _Пр I П о ^- П ,

С целью установления предельных значений размеров рабочих поверхностей деталей шестеренных гидронасосов по величинам износов [17; 18], а также соответствующим значениям на момент исследования наработок строится динамика изнашивания [19–22]:

и ( t ) = Vt⁸ + Z + и 1 , (4)

где u(t) – износ рабочих поверхностей деталей, мкм; Vc – показатель скорости изменения износов рабочих поверхностей деталей u при t = 1, уменьшенный в θ раз; t – наработка до предельного состояния гидронасоса (ресурс); θ – показатель степени; Z – отклонение фактического изменения износов дета- лей и от теоретической кривой; и 1 - показатель, характеризующий приработку деталей [23].

Наиболее правильным подходом в определении предельных и допустимых значений износов рабочих поверхностей деталей гидронасосов является множественная регрессия, которая показывает связь нескольких независимых переменных с зависимой переменной.

Зависимой переменной является параметр технического состояния гидронасоса (коэффициент подачи), а независимыми переменными – износы рабочих поверхностей деталей.

Материалы и методы

Оценка технического состояния бывших в эксплуатации круглых шестеренных насосов осуществлялась по допустимому значению коэффициента подачи n Q . Допустимое значение коэффициента подачи составляет 0,5 от предельного [24]. Для круглых шестеренных насосов навесных гидросистем тракторов нормативное предельное значение коэффициента подачи составляет 0,4 [2]. Тогда допустимое значение коэффициента подачи составит 0,7.

Определение значения коэффициента подачи насоса осуществляется на стенде КИ-28097М-ГОСНИТИ по описанной ниже методике.

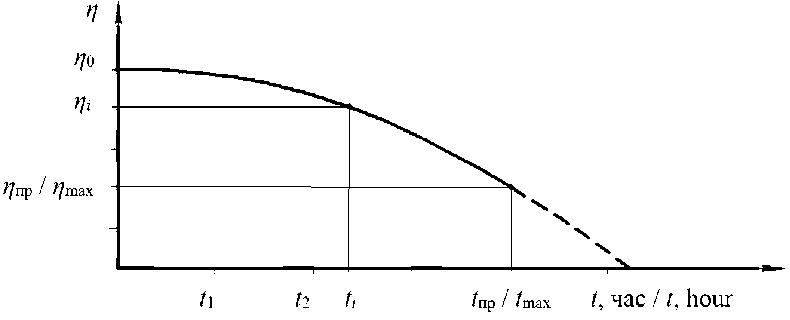
Р и с. 2. Характер зависимости изменения коэффициента подачи насоса от наработки

F i g. 2. Character of dependence of change of pump delivery rate on operating time

Используя соответствующие приспособления, насос устанавливают на стенд. Гидрорукав напорной секции насоса соединяют с дросселем стенда, а гидрорукав всасывания – с баком стенда. Поворотом рукоятки дросселя стенда определяют максимальное давление, развиваемое насосом.

В экспериментальные исследования входили гидронасосы, максимально развиваемое давление которых превышало номинальное значение.

Поворотом рукоятки дросселя стенда устанавливается номинальное для испытуемого насоса давление. Обнулив счетчик циклов, рукоятку трехходового крана поворачивают в положение «включено». Выбрав начало отсчета на шкале счетчика жидкости, включают счетчик циклов, по которому фиксируется контрольный объем масла: для гидронасосов марки НШ 32А – 60 л; для НШ 50А – 100 л; для НШ 100А – 200 л. Выключив счетчик импульсов, по зависимости, представленной на рисунке 3, определяют действительную подачу насоса Qд отдельно для каждой модели.

Затем по отношению действительной объемной подачи Q к теоретической объемной подаче Q _т определяется коэффициент подачи η_Q .

Для проведения микрометражных исследований приняты следующие поверхности: цапфы валов, наружный диаметр по вершинам зубьев, ширина зубъев шестерен, поверхности плати-ков, полуотверстия под цапфы валов поджимной обоймы, колодцы под шестерни валов поджимной обоймы.

Результаты исследования

Статистические параметры результатов стендовых испытаний технического состояния круглых шестеренных гидронасосов для исследуемых моделей представлены в таблице 1.

Для определения отношения независимых выборок к одной генеральной совокупности в статистических исследованиях широкое применение нашел критерий Стьюдента ( t -критерий). Од-

Qд, см3/об /

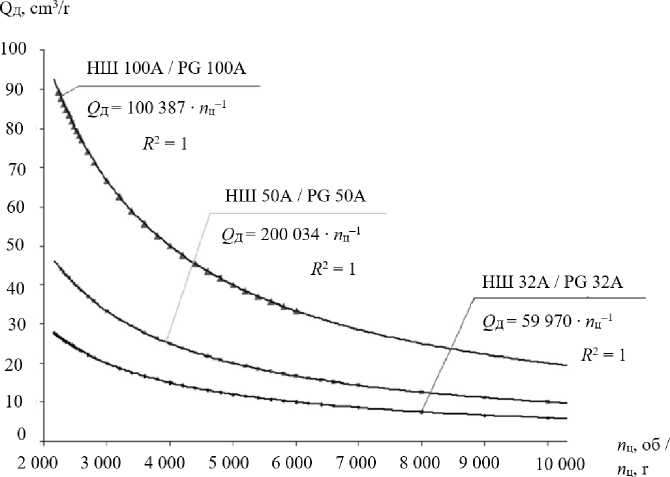
Р и с. 3. Зависимость действительной подачи шестеренных гидронасосов от числа циклов

F i g. 3. Dependence of the actual supply of gear hydraulic pumps on the number of cycles Technologies and maintenance means in agriculture 431

Т а б л и ц а 1

T a b l e 1

Статистические параметры выборок круглых шестеренных гидронасосов Statistical parameters of samples of round gear hydraulic pumps

Модель гидронасоса / Hydraulic pump model N X σ Диапазон значений / Range of values pW Xmax Xmin НШ 32А / PG 32А 50 0,3358 0,083 0,418 0,153 0,00000 НШ 50А / PG 50А 50 0,3327 0,082 0,415 0,152 0,00000 НШ 100А / PG 100А 50 0,3359 0,083 0,418 0,153 0,00000 нако для применения данного параметра необходима проверка нормальности распределения полученных выборок, которая осуществляется применением критерия Шапиро ‒ Уилка (W).

Нулевая гипотеза гласит: «распределение измерений для каждой исследуемой модели насосов близко к нормальному, альтернативная – нет. Если уровень значимости текущего значения W -критерия p_W выше принятого значения p = 0,05, то имеет место нулевая гипотеза и наоборот» [25].

Согласно результатам таблицы 1 уровень значимости W -критерия p_W < 0,05, что говорит об отличии распределения значений выборок η_Q исследуемых гидронасосов от нормального распределения.

В данном случае для оценки возможности объединения независимых выборок возникает необходимость применения критериев непараметрической статистики, в частности критерия Краскела - Уоллиса (KW). Согласно ре зультатам проверки выборок на расходимость критерий Краскела – Уоллиса составил pKW = 0,4792, что больше порогового значения p = 0,05 и подтверждает возможность их объединения.

Методом максимального правдоподобия с применением программы Statistica осуществлялось определение параметров закона распределения объединенной выборки nQ- Качество подгонки оценивалось по критерию Холландера – Прошана ( HP ).

Гипотеза звучит так: «закон распределения коэффициента подачи насосов не согласуется с законом распределения Вейбулла, альтернативная - согласуется. Если уровень значимости текущего значения критерия p HP ниже принятого значения р = 0,05, то имеет место нулевая гипотеза и наоборот» [25].

Коэффициент подачи насосов подчиняется закону распределения Вейбулла, парметры которого представлены в таблице 2. При помощи модуля «вероятностный калькулятор» про-

Т а б л и ц а 2

T a b l e 2

Параметры закона распределения Вейбулла коэффициента подачи насосов Parameters of the Weibull distribution law pump feed ratio

Математическое ожидание функции / Expectation of function μ 0,3420 Параметры закона распределения Вейбулла / The parameters of the law of Weibull distribution α 0,3654 b 5,2890 Критерий Холландера – Прошана / Hollander – Proshan Criterion pHP 0,1670 граммы Statistica определялось математическое ожидание двухпараметрической функции μ.

Согласно функции распределения коэффициента подачи, представленной на рисунке 4, доля эксплуатируемых в запредельном состоянии круглых шестеренных гидронасосов составляет 81 %.

Результаты микрометражных исследований рабочих поверхностей деталей шестеренных гидронасосов показали, что уровень значимости вариационных рядов износов менее 0,05, что отвергает нулевую гипотезу нормальности распределения выборок. В связи с этим с целью сравнения выборок на расходимость применим критерий Краскела – Уоллиса (KW) (таблица 3).

Согласно результатам проверки выборок на расходимость уровень значимости критерия Краскела – Уоллиса превышает значение 0,05, что отвергает гипотезу их расхождения.

Применив программное обеспечение Statistica, методом максимального правдоподобия определили параметры закона распределения объединенных выборок износов, а математическое ожидание функции – при помощи «вероятностного калькулятора». Оценка

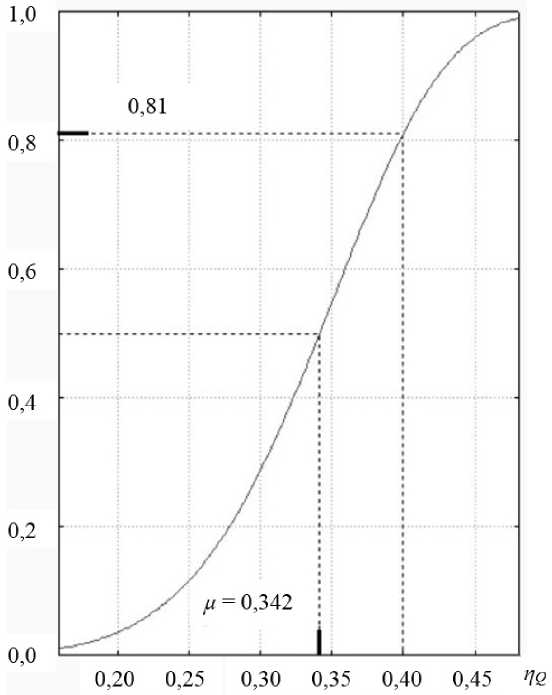
Р и с. 4. Функция распределения коэффициента подачи насоса

F i g. 4. Distribution function of the pump delivery rate

Т а б л и ц а 3

T a b l e 3

Сравнение исследуемых выборок по KW -критерию Comparison of the studied samples by the KW -criterion

Выборка / Sample KW-критерий / KW-criteria Износ цапфы ведомой шестерни UC1 , мкм / Wear of the axle driven gear UC1 , μm 0,0841 Износ цапфы ведущей шестерни UC2 , мкм / Wear of the lead gear axle UC2 , μm 0,0882 Износ полуотверстий под шестерню ведомую поджимной обоймы UP1 , мкм / Wear of half-holes for driven gear of pressure holder UP1 , μm 0,0785 Износ полуотверстий под шестерню ведущую поджимной обоймы UP2 , мкм / Wear of semi-holes for the drive gear of pressure holder UP2, μm 0,0836 Износ по ширине зубьев ведомой шестерни US1H.Z, мкм / Wear over the width of the teeth of the driven gear US1H.Z, μm . 0,0801 Износ по ширине зубьев ведущей шестерни U S2H. Z, мкм / Wear over the width of the teeth of the drive gear US2H.Z, μm 0,0820 Износ рабочей поверхности платика первого U P1L, мкм / Wear of the working surface of the first plate U P1L, μm 0,0880 Износ рабочей поверхности платика второго U P2L, мкм / Wear of the working surface of the second plate UP2L, μm 0,0827 Износ по вершинам зубьев ведомой шестерни UV1. Z, мкм / Wear on tips of driven gear teeth UV1. Z, μm . 0,0968 Износ по вершинам зубьев ведущей шестерни UV2. Z, мкм / Wear on tips of drive gear teeth U 2 , μm V. Z 0,0924 Износ колодцев под ведомую шестерню поджимной обоймы UK1 , мкм / Wear of wells for driven gear of pressure holder UK1 , μm 0,0946 Износ колодцев под ведущую шестерню поджимной обоймы UK2, мкм / Wear of wells for the drive gear of the pressure cage UK2 , μm 0,1001 качества подгонки осуществлялась при помощи критерия Холландера – Прошана (HP). Статистические характеристики объединенных выборок и параметры законов распределения представлены в таблице 4.

В работе В. В. Конева и коллег для проведения регрессионного анализа рекомендуется применять круглые шестеренные гидронасосы, у которых зафиксированы значения коэффициентов подачи и соответствующие значения износов деталей [24].

При проведении регрессионного анализа зависимой переменной принят коэффициент подачи шестеренного гидронасоса η_Q , а независимыми переменными: U_C ¹ – износ цапф шестерни ведомой, мкм; U_C ² – износ цапф шестерни ведущей, мкм; U _P ¹ – износ полуотверстий под шестерню ведомую обоймы поджимной, мкм; U _P ² – износ

Т а б л и ц а 4

T a b l e 4

Статистические характеристики объединенных износов рабочих поверхностей деталей бывших в эксплуатации гидронасосов

Statistical characteristics of combined wear of working surfaces of used hydraulic pump details

Объединенные выборки / Conbined samples X Диапазоны износов / Wear ranges σ Параметры Вейбулла распределения / Parameters of the Weibull distribution μ pHP Xmax Xmin a b UC1 1 2 14,5 4 42 7,76 16,44 2,00 13,70 0,581 UC2 15,9 4 38 7,35 18,05 2,34 15,40 0,622 UP1 136,0 32 367 81,43 154,00 1,80 125,60 0,461 UP2 139,1 32 389 83,20 157,54 1,81 128,60 0,449 US1H.Z 79,6 18 224 41,70 90,14 2,04 75,30 0,779 US2H.Z 82,4 16 235 44,08 93,33 1,99 77,60 0,774 UP1L 171,1 25 440 106,98 191,30 1,63 152,80 0,958 UP2L 174,2 26 446 106,91 195,20 1,67 156,70 0,959 UV1.Z 79,1 12 211 43,23 89,45 1,94 74,10 0,774 UV2.Z 81,8 16 219 43,12 92,69 2,03 77,38 0,685 UK1 31,9 8 72 15,28 36,15 2,25 30,72 0,706 UK2 35,1 10 81 16,47 39,82 2,31 33,98 0,707 полуотверстий под шестерню ведущую обоймы поджимной, мкм; U S1H. Z – износ по ширине зубьев шестерни ведомой, мкм; US2H. Z – износ по ширине зубьев шестерни ведущей, мкм; UP1L – износ рабочей поверхности платика первого, мкм; UP2L – износ рабочей поверхности платика второго, мкм; UV1. Z – износ по вершинам зубьев шестерни ведомой, мкм; UVZ - износ по вершинам зубьев шестерни ведущей, мкм; UXK - износ колодцев под шестерню ведомую обоймы поджимной, мкм; UK2 – износ колодцев под шестерню ведущую обоймы поджимной, мкм.

Однородность исследуемых выборок проверяли по критерию Манна – Уитни. Статистические параметры вариационных рядов представлены в таблице 5.

Согласно результатам, представленным в таблице 5, уровень значимости критерия Манна - Уитни p U для исследуемых выборок значительно превыша-

Т а б л и ц а 5

T a b l e 5

Статистические параметры и оценка однородности объединенных выборок Statistical parameters and estimation of homogeneity of combined samples

Объединенные выборки / Conbined samples N X Диапазон износа / Wear range σ pU Xmax Xmin UC1 1 2 120 14,800 4,000 42,000 8,79 0,790 UC2 16,900 2,000 47,000 11,42 0,681 UP1 143,000 39,000 365,000 75,37 0,311 UP2 145,000 25,000 380,000 86,10 0,577 US1H.Z 80,500 11,000 200,000 45,68 0,926 US2H.Z 81,600 16,000 209,000 46,75 0,821 UP1L 166,900 18,000 440,000 106,74 0,863 UP2L 176,500 44,000 439,000 95,45 0,550 UV1.Z 81,800 10,000 236,000 52,04 0,745 UV2.Z 85,400 10,000 210,000 45,45 0,595 UK1 32,820 4,000 108,000 22,72 0,481 UK2 35,200 8,000 110,000 18,50 0,817 ηQ 0,311 0,130 0,418 0,09 0,128 ет 5-процентный пороговый уровень, что говорит об их однородности.

Уравнение линейной множественной регрессии в натуральном масштабе имеет вид:

П с = в о + в 1 • U C + в 2 • U C +

+ ^в 3 • U P ⁺ ^в 4 • U P ⁺ ^в 5 • ^USH . Z ⁺

+ ^в 6 • ^USH . Z ⁺ ^в 7 • ^UPL ⁺

^+в 8 • ^UPL ⁺ ^в 9 • ^UV. Z ⁺

⁺ ^в 10 • ^UV . Z ⁺ ^в 11 • ^UК ⁺ ^в 12 • U K • ⁽⁵⁾

Корреляционный анализ уравнения (5) показал, что коэффициент мно- жественной корреляции между зависимой и независимыми переменными равен R = 0,986, а коэффициент детерминации R2 = 0,974 (R2 = 0,971), то есть полученное уравнение регрессии показывает 97-процентный разброс значений коэффициента подачи относительно среднего значения бывших в эксплуатации шестеренных гидронасосов.

В таблице 6 представлены значения попарных коэффициентов корреляции между зависимыми и независимыми факторами.

Согласно данным таблицы 6 наблюдается отсутствие связи между независимыми факторами, что позволяет их

Т а б л и ц а 6

T a b l e 6

fl ,o

о О

s s fl

1 Ph ex s s

fl s fl

-e-s

^D O\

CM b< tj

(M O\

^D O\

oo O\

^D O\

oo O\

O\ O\

^D O\

O\ O\

^D O\

O\ O\

^D O\

bD O\

^D O\

o^ 7

b^u

O\ O\

^D O\

ь^и

b^-

N b

ь^0-

N br

eq b< tj

применять в многофакторном регрессионном анализе.

По результатам оценки неизвестных коэффициентов уравнения (5) выявлена их статистическая значимость, в связи с чем они приняты для дальнейшего анализа.

Коэффициенты статистической связи между независимыми факторами и зависимой переменной, полученные многофакторным регрессионным анализом, представлены в таблице 7.

Согласно результатам таблицы 7 для каждого независимого фактора уровень значимости критерия Стьюдента ( p_t ) ниже принятого значения p_t = 0,005, что подтверждает связь коэффициента по-

Том 30, № 3. 2020

дачи насоса НШ серии А от всех принятых для исследования износов рабочих поверхностей деталей.

Таким образом, математическая модель связи коэффициента подачи насоса и независимых факторов запиcывается:

nQ = 0,450879 - 0,005507 • UC -

-0,005588 • UC - 0,000631 • U2 -

0,00043 • U2 + 0,000772 • UL 7 +

PSH . Z

+0,000776 • U2„ 7 - 0,000255 • U* -

SH . ZPL

-0,000145 • UpL + 0,000407 • UV.Z +

+0,000426 • U27 + 0,000646 • U* +

V . Z K

+0,001159 • UK (6)

Т а б л и ц а 7

T a b l e 7

Коэффициенты статистической связи между независимыми факторами и зависимой переменной

Coefficients of the statistical relationship between independent factors and a dependent variable

N = 120	Множественный регрессионный анализ: зависимая переменная ^ q / Multiple regression analysis: dependent variable ƞ_QR = 0,986; R ² = 0,974; F = 334,45; S_{̅v / ∑z} = 0,015
N = 120	b i	Стандартная ошибка b i / Standard error b i	β_i	Стандартная ошибка β i / Standard error β i	t (107)	p_t- уровень / p_t -level
Свободный член β ₀ / Free member β ₀	–	–	0,450879	0,005249	85,89374	0,000000
U C ¹	–0,536494	0,101716	–0,005507	0,001044	–5,27441	0,000001
^UC ²	–0,706618	0,110604	–0,005588	0,000875	–6,38873	0,000000
U P ¹	–0,526533	0,061685	–0,000631	0,000074	–8,53585	0,000000
U P ²	–0,409875	0,157847	–0,000430	0,000165	–2,59665	0,010737
U S ¹ H . Z	0,390446	0,160855	0,000772	0,000318	2,42731	0,016881
U S ² H . Z	0,402034	0,125289	0,000776	0,000242	3,20886	0,001759
U P ¹ L	–0,302038	0,094454	–0,000255	0,000080	–3,19772	0,001822
_UP 2 _L	–0,153396	0,064721	–0,000145	0,000061	–2,37012	0,019573
U V ¹. Z	0,234337	0,109213	0,000407	0,000189	2,14569	0,034159
^UV ². Z	0,214251	0,053170	0,000426	0,000106	4,02955	0,000105
U K ¹	0,162526	0,068433	0,000646	0,000272	2,37496	0,019331
^UK ²	0,237451	0,066637	0,001159	0,000325	3,56335	0,000548

Высокая значимость полученной регрессии (6) подтверждена проверкой по критерию Фишера, согласно результатам которой расчетное значение составило F = 334,45 , что значительно больше критического F _кр = 12,107.

Значение стандартной ошибки (меры рассеяния) экспериментальных значений относительно регрессионной прямой составило 5 -/= 0,015 , что отличается от среднего значения функции отклика, равного 0,016, менее чем на 5 %.

Проведенная оценка остатков по критерию Дарбина – Уотсона показала: d = 1,8 > DU - 12( d _кр) = 1,78, что подтверждает независимость остатков регрессионной модели (6) на 5-процентном уровне [26].

С целью проверки полученной регрессионной модели (6) на адекватность рассмотрим график распределения остатков, представленный на рисунке 5.

Из графика, представленного на рисунке 5, видно, что остатки функции отклика имеют нормальное распределе- ние, что также подтверждает уровень значимости W-критерия, равный 0,062.

Из представленных на рисунке 6 экспериментальных величин остатков следует, что они разбросаны хаотически, слабо коррелированы между собой, а также отсутствует закономерность в их поведении.

Согласно исследованным критериям полученная математическая модель (6) адекватно описывает связь коэффициента подачи насоса с независимыми факторами (износами).

Проверка регрессии (6) по среднему значению показала, что расчетное значение η_Q = 0,3112 превышает среднее значение функции отклика ^ q = 0,3111, полученного экспериментально, менее чем на 0,03 %.

Согласно анализу значений стандартизированного коэффициента регрессии независимых факторов по модулю | b_i | наибольшее влияние на зависимую переменную n Q оказывают: износ поверхности цапф шестерни ведущей (| b_i | = = |0,706618|); износ поверхности цапф

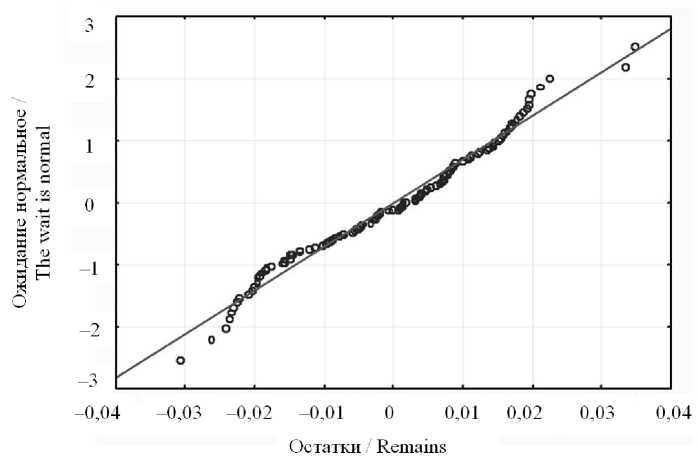
Р и с. 5. Графическая зависимость нормального распределения остатков

F i g. 5. The graphical dependence of the normal distribution of the remains

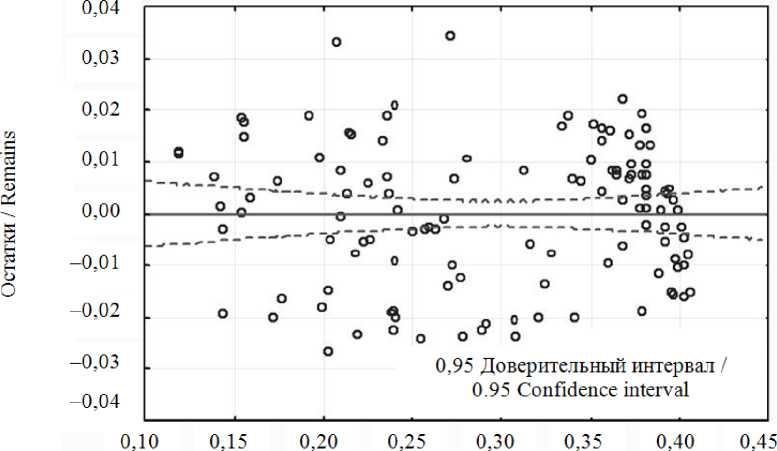
Предсказанные значения / Predicted value

Р и с. 6. Разброс экспериментальных величин остатков и удаленных остатков

F i g. 6. Spread of experimental values of remains and deleted remfins шестерни ведомой (b| = |0,53 6494|); износ поверхности подшипниковой полуобоймы под шестерню ведомую (|bi| = = |0,526533|); износ поверхности подшипниковой полуобоймы под шестерню ведущую (|bi| = |0,40985|).

Из анализа принципа работы, конструкционных особенностей круглых шестеренных насосов и проведенных статистических исследований можно утверждать, что данные сопряжения являются ресурсоопределяющими для агрегата в целом.

Методом крутого восхождения найдем значения износов рабочих поверхностей деталей насоса, соответствующие предельному значению коэффициента подачи, равному η_Q = 0,4.

Произведение Р, ' ^X i вычислялось по каждому фактору (табл. 8). Максимальное значение фактора составило

0,1257 для U _C ² , в связи с чем этот фактор принят за базовый.

Параметры метода крутого восхождения представлены в таблице 8, где: X _ш - начальный шаг эксперимента; ^ - значение сдвига крутого восхождения по базовому фактору, µ = 0,1; λ _ш( β_i ∙ Δ X_i ) – шаг фактора.

Согласно таблице 8 предельное значение коэффициента подачи гидронасоса, равное 0,4, соответствует 11-му шагу. В связи с этим установлены предельные значения износов рабочих поверхностей деталей круглых шестеренных гидронасосов: износ цапфы шестерни ведомой U_C ¹ = 23 мкм; износ цапфы шестерни ведущей U_C ² = 25 мкм; износ полуотверстий под шестерню ведомую поджимной обоймы U p = 202 мкм; износ полуотверстий под шестерню ведущую поджимной обоймы U _P ² = 203 мкм;

Т а б л и ц а 8

T a b l e 8

СУ

5 й о

Ри

ч СУ К

ОО 04

(XI ОО ОО 04

Я 04

оо

40 04

X ь<

ОО

Г1

ГЧ

ОО

04"

(Х1^ 04" 40

оС

Г1

°ч

ХГ

*4 оС

40"

(*ч

40" 40

40^

ОО^ 40"

(XI

ОО

Г1

ГЧ

ъ^

гч

04 04

СП

Г1

40^

°\ 40"

(Х1^ оо" 40

04"

2 ОО

2 оС ОО 40

оС

я^

Г1

ОО (XI

Я^

ОО

ГЧ 04

Г1

ОО

04'

04"

(XI (XI

(Х1^ я

(xf 04 ri

Г1

ОО

40" 04

Г1

ОО

ОО оо" гч

2 оС

(Х1"

(xf

Г1

°ч

О,

ОО

40" Г1

оС

оо

(xf

(Х1"

Г1

(xf ГЧ

Cxf

(xf

(XI

Я^

(XI (XI

оо

(XI

Я^

04 (XI

ь^0-

(М ri

2 о

оо оо"

40"

(xf

(XI

оо"

(XI

40^

°\

(Х1^

Г1

(XI

ГЧ

04 оо

Я cxf

О1

40" (XI

04 (XI

ь^и

Г1

оо"

°\

ХГ

°\

°\ Я

°ч 40"

(XI

оо" (XI

40^

(xf

5 У

с^

й а ^

'—¹

О1

(XI

KTSJ износ по ширине зубьев шестерни ведомой USH. Z = 106 мкм; износ по ширине зубьев шестерни ведущей U S2H. Z = 113 мкм; износ рабочей поверхности плати-ка первого UpL = 229 мкм; износ рабочей поверхности платика второго UpL = 242 мкм; износ по вершинам зубьев шестерни ведомой UV1. Z = 123 мкм; износ по вершинам зубьев шестерни ведущей Ш Z = 110 мкм; износ колодцев под шестерню ведомую поджимной обоймы UK1 = 56 мкм; износ колодцев под шестерню ведущую поджимной обоймы UK = 59 мкм. Коэффициент подачи гидронасосов при округленных значениях износов составил 0,398.

Обсуждение и заключение

В результате проведенных стендовых испытаний бывших в эксплуатации круглых шестеренных гидрона-

Том 30, № 3. 2020

сосов можно сделать вывод, что 81 % насосов эксплуатировался в запредельном состоянии.

По регрессионной модели связи коэффициента подачи круглых шестеренных гидронасосов с износа-ми рабочих поверхностей деталей установлены их предельные значения: U^X_C = 23 мкм, U C = 25 мкм, U _P ¹ = 202 мкм, U _P ² = 203 мкм, U' = 106 мкм, U 2_Н ₇ = 113 мкм,

SH . Z SH ^. Z

U_P ¹ _L = 229 мкм, U_P ² _L = 242 мкм, U ¹ = 123 мкм, U ² = 110 мкм,

V . Z V _. Z

U_K ¹ = 56 мкм, U_K ² = 59 мкм. По этим значениям износов рабочих поверхностей деталей круглых шестеренных гидронасосов принимается решение об их восстановлении.

Поступила 06.02.2020; принята к публикации 16.04.2020; опубликована онлайн 30.09.2020

Все авторы прочитали и одобрили окончательный вариант рукописи.

Список литературы Оценка технического состояния круглых шестеренных гидронасосов навесных гидросистем тракторов

Величко, С. А. Ресурс и допустимое значение коэффициента полезного действия шестеренных круглых гидронасосов / С. А. Величко, Ф. Х. Бурумкулов, П. А. Ионов // Техника в сельском хозяйстве. - 2011. - № 2. - С. 26-28. - URL: http://Miantru/catalog/psuHbr?SHOW_ONE_ BOOK+4130E2 (дата обращения: 06.08.2020).
Величко, С. А. Оценка показателей G-процентного ресурса новых и отремонтированных по новой технологии агрегатов навесных гидросистем тракторов / С. А. Величко, П. В. Сенин, А. В. Мартынов // Энергоэффективные и ресурсосберегающие технологии и системы. - 2016. -С. 77-87.
Бурумкулов, Ф. Х. Ресурсосбережение на основе повышения межремонтной наработки изделия / Ф. Х. Бурумкулов, С. А. Величко, П. В. Чумаков // Труды ГОСНИТИ. - 2012. - № 1. -С. 110-114.
Величко, С. А. Ремонт агрегатов машин с восстановлением показателей безотказности и долговечности на уровне нового изделия / С. А. Величко // Труды ГОСНИТИ. - 2013. - Т. 111, № 2. - С. 19-23. - Рез. англ.
Басинюк, В. Л. Система мобильного мониторинга гидропривода навесных устройств энергонасыщенных тракторов / В. Л. Басинюк, А. С. Калиниченко, И. Н. Усс [и др.] // Наука и техника. - 2013. - № 5. - С. 49-54. - URL: https://sat.bntu.by/jour/article/view/231 (дата обращения: 06.08.2020). - Рез. англ.
Сенин, П. В. Восстановление круглых шестеренных гидронасосов типа НШ-К комбинированным методом / П. В. Сенин, Е. А. Нуянзин, П. А. Ионов [и др.] // Тракторы и сельхозмашины. -2012. - № 10. - С. 42-43. - Рез. англ.
Рылякин, Е. Г. Исследование интенсивности изнашивания ресурсоопределяющих сопряжений гидронасосов / Е. Г. Рылякин // Молодой ученый. - 2014. - № 8. - С. 243-246. - URL: https:// moluch.ru/archive/67/11188 (дата обращения: 06.08.2020). - Рез. англ.
Котомчин, А. Н. Восстановление деталей узлов и агрегатов техники, работающих при гидроабразивном изнашивании / А. Н. Котомчин, Е. Ю. Ляхов. - DOI 10.31044/1684-2561-2019-0-58-12 // Ремонт. Восстановление. Модернизация. - 2019. - № 5. - С. 8-12. - URL: http://www.nait.ru/ journals/number.php?p_number_id=2924 (дата обращения: 06.08.2020). - Рез. англ.
Коломейченко, А. В. Износостойкость МДО-покрытий, сформированных на алюминиевых сплавах АОЗ-7 и АК7Ч / А. В. Коломейченко, В. Н. Логачев // Ремонт. Восстановление. Модернизация. - 2006. - № 8. - С. 44-46. - URL: http://www.nait.ru/journals/number.php?p_number_id=444 (дата обращения: 06.08.2020). - Рез. англ.
Хромов, В. Н. Технология восстановления корпуса шестеренного насоса термопластическим деформированием / В. Н. Хромов, И. К. Сенченков, А. В. Коломейченко [и др.] // Ремонт. Восстановление. Модернизация. - 2006. - № 9. - С. 11-15. - URL: http://www.nait.ru/journals/number. php?p_number_id=445 (дата обращения: 06.08.2020). - Рез. англ.
Коломейченко, А. В. Анализ внутренних напряжений корпуса восстановленного шестеренного насоса / А. В. Коломейченко, В. Н. Логачев // Тракторы и сельхозмашины. - 2010. - № 7. -С. 33-34.
Величко, С. А. Восстановление шестерен гидронасосов НШ-А методом свободных ремонтных размеров / С. А. Величко, А. В. Мартынов // Тракторы и сельхозмашины. - 2015. - № 2. -С. 47-49.
Бурумкулов, Ф. X. Повышение ресурса агрегатов созданием на рабочих поверхностях деталей наноструктурированных покрытий / Ф. X. Бурумкулов, С. А. Величко, А. М. Давыдкин [и др.] // Технология металлов. - 2008. - № 1. - С. 2-7.
Бурумкулов, Ф. Х. Наноэлектротехнологии для повышения межремонтного ресурса агрегатов машинно-тракторного парка сельского хозяйства / Ф. Х. Бурумкулов, С. А. Величко, В. И. Иванов [и др.] // Труды ГОСНИТИ. - 2007. - Т. 99. - С. 85-94.
Shia, L. Numerical Simulation and Experimental Study on the Comparison of the Hydraulic Characteristics of an Axial-Flow Pump and a Full Tubular Pump / L. Shia, W. Zhanga, H. Jiaoa [et al.]. -DOI 10.1016/j.renene.2020.02.082 // Renewable Energy. - 2020. - Vol. 153. - Pp. 1455-1464. - URL: https://www.sciencedirect.com/science/article/abs/pii/S0960148120302779?via%o3Dihub (дата обращения: 06.08.2020).
Bedotti, A. Dynamic Modelling of the Swash Plate of a Hydraulic Axial Piston Pump for Condition Monitoring Applications / A. Bedotti, M. Pastori, F. Scolari [et al.]. - DOI 10.1016/j.egypro.2018.08.077 // Energy Procedia. - 2018. - Vol. 148. - Pp. 266-273. - URL: https://www.sciencedirect.com/science/ar-ticle/pii/S1876610218303709?via%3Dihub (дата обращения: 06.08.2020).
Gao, Y. Wavelet Packet and Residual Analysis Based Method for Hydraulic Pump Health Diagnosis / Y. Gao, Q. Zhang. - DOI 10.1243/09544070JAUT0253 // Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering. - 2006. - Vol. 220, no. 6. - Pp. 735-745. -URL: https://journals.sagepub.com/doi/10.1243/09544070JAUT0253 (дата обращения: 06.08.2020).
Casoli, P. Overall Efficiency Evaluation of a Hydraulic Pump with External Drainage through Temperature Measurements / P. Casoli, F. Campanini, A. Bedotti [et al.]. - DOI 10.1115/1.4039084 // Journal of Dynamic Systems, Measurement and Control. - 2018. - Vol. 140, Issue 8. - 9 p. - URL: https:// asmedigitalcollection.asme.org/dynamicsystems/article-abstract/140/8/081005/439974/Overall-Efficien-cy-Evaluation-of-a-Hydraulic-Pump?redirectedFrom=fulltext (дата обращения: 06.08.2020).
Frith, R. H. Comparison of an External Gear Pump Wear Model with Test Data / R. H. Frith, W. Scott. - DOI 10.1016/0043-1648(95)06845-7 // Wear. - 1996. - Vol. 196, no. 1. - Pp. 64-71. - URL: https://www.sciencedirect.com/science/article/abs/pii/0043164895068457?via%3Dihub (дата обращения: 06.08.2020).
Battarra, M. On the Assessment of Lumped Parameter Models for Gearpump Performance Prediction / M. Battarra, E. Mucchi. - DOI 10.1016/j.simpat.2019.102008 // Simulation Modelling Practice and Theory. - 2019. - Vol. 99. - Pp. 34-40. - URL: https://www.sciencedirect.com/science/article/abs/pii/ S1569190X19301418?via%3Dihub (дата обращения: 06.08.2020).
Han, M. Reliability Analysis of a Hydraulic Pump / M. Han // Journal of Mechanical Engineering. - 2002. - Vol. 38, no. 1. - Pp. 10-15. - URL: https://www.researchgate.net/publication/245444192_ Reliability_analysis_of_a_hydraulic_pump (дата обращения: 06.08.2020).
Tkac, Z. Experimental Hydraulic Device for the Testing of Hydraulic Pumps and Liquids / Z. Tkac, J. Kosiba, L. Hujo [et al.]. - DOI 10.24874/ti.2018.40.01.14 // Tribology in Industry. - 2018. -Vol. 40, no. 1. - Pp. 149-155. - URL: http://www.tribology.rs/journals/2018/2018-1/2018-1-14.html (дата обращения: 06.08.2020).
Пумпур, Е. В. Применение аддитивных технологий для ремонта гидропривода горных машин на примере шестеренного насоса НШ-32 / Е. В. Пумпур // Проблемы разработки месторождений углеводородных и рудных полезных ископаемых. - 2016. - № 1. - С. 311-314.
Конев, В. В. Экспериментальные исследования гидропривода строительно-дорожных машин / В. В. Конев, С. П. Пирогов, Д. М. Бородин [и др.] // Современные проблемы науки и образования. - 2015. - № 1. - С. 68. - URL: https://www.science-education.ru/ru/article/view?id=17665 (дата обращения: 06.08.2020). - Рез. англ.
Боровиков, В. П. Мнение профессионала / В. П. Боровиков // Автотранспортное предприятие. - 2010. - № 2. - С. 14-15.
Боровиков, В. П. Об асимптотическом распределении статистик, основанных на выборочных промежутках, с оцененными параметрами / В. П. Боровиков. - DOI 10.4213/tvp2791// Теория вероятности и ее применения. - 1996. - Т. 41, № 1. - С. 181-186. - URL: http://www.math-net.ru/php/archive.phtml?wshow=paper&jrnid=tvp&paperid=2791&option_lang=rus (дата обращения: 06.08.2020). - Рез. англ.

Еще

Статья научная