Оценка технического состояния стержневых элементов металлоконструкций с несовершенствами формы

Стержневые элементы, работающие на сжатие, являются неотъемлемой частью ферменных конструкций, широко применяемых в технике. Несущая способность сжатого стержня заданного сечения и размеров определяется расчетным сопротивлением материала и величиной случайного эксцентриситета, который, в свою очередь, обусловлен граничными условиями и наличием выгибов. Результаты обследований несущих металлоконструкций подъемно-транспортных машин и производственных зданий свидетельствуют о том, что отклонения формы стержневых элементов от прямолинейной распространены повсеместно. Несовершенства формы имеют широкий спектр типов и относительных параметров и могут быть как дефектами, вызванными отступлениями от технических норм, регламентирующих изготовление и монтаж конструкций, так и повреждениями, возникающими вследствие нарушений правил технической эксплуатации. Основной причиной возникновения искривлений при эксплуатации ферм является перегрузка элементов от проектных или непроектных воздействий (рис. 1), а также несоответствие принятой расчетной схемы действительной работе конструкций (рис. 2). В совокупности искривления стержневых элементов общего и местного характера составляют около 60-80 % от общего числа дефек тов, встречающихся в процессе технического диагностирования.

При выполнении проектных расчетов центральносжатых элементов по действующим строительным нормам [1-3] закладывается величина выгиба, равная 1/750 длины стержня. Однако, как показывают результаты выборочных исследований, существующая технология изготовления металлоконструкций не в состоянии обеспечить прямолинейность стержней ферм, отчасти даже в пределах стандартов на изготовление. По данным авторов [4; 5], величина погнутости превосходит нормативную примерно у 10-15 % стержней. В процессе эксплуатации наблюдается рост как числа поврежденных элементов (более чем в 2 раза), так и размеров искривлений. Статистические характеристики относительных погнутостей имеют положительную корреляцию со значениями гибкости стержней.

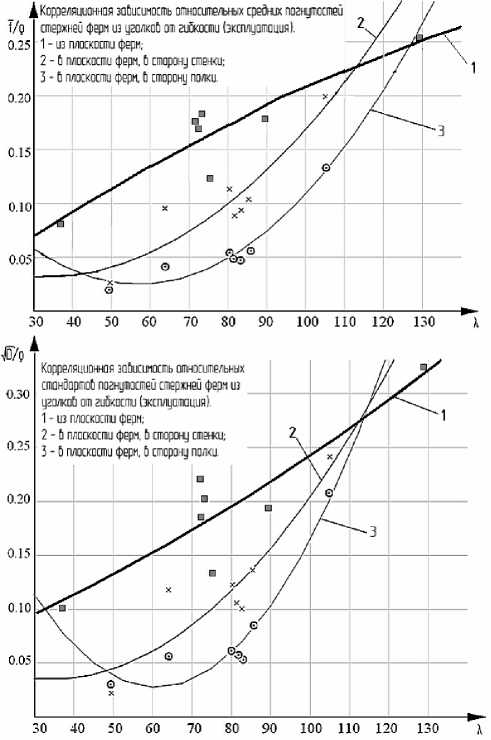
Были рассмотрены статистические данные по дефектам формы сорока ферм покрытия с сечениями из спаренных в тавр уголков, построены гистограммы и вычислены статистические характеристики параметров повреждений. Построение графиков зависимости относительного среднего значения погнутости (в долях от радиуса ядра сечения) и его среднего квадратического отклонения от гибкости указало на наличие корреляционной зависимости между этими величинами. Уравнения кривых регрессии разыскивались в виде квадратных парабол:

f / р = ( a 1 X^T + b 1 X + c 1 )10 ^{- 5} , D/ р / р = ( a₂ Х^г + b ₂ X + c ₂ )10 ^{- 5} .

Значения коэффициентов, найденных методом наименьших квадратов, приведены в таблице, графики зави-симостей// р и 1У - /р от X показаны на рис. 3.

По результатам статистического анализа также хорошо подтверждается гипотеза о значимости выборочного коэффициента корреляции между числом повреждений и сроком эксплуатации.

Для аппроксимации опытных полигонов распределения искривлений наилучшим образом подходят двух модальные законы распределения, характерные для суммы двух разнородных распределений, первое из которых описывает малые искривления стержней, возникающие при изготовлении, а второе - значительные искривления, обусловленные грубыми нарушениями, допускаемыми при транспортировании, монтаже и, в особенности, при эксплуатации. Первое распределение лучше описывается полунормальным законом распределения, связанным с накоплением и суммированием отдельных воздействий, второе - экспоненциальным законом (частный случай закона Вейбулла, закона распределения при наличии в системе так называемого «слабого звена») [6].

Рис. 1. Выгибы элементов ферм из-за непроектных воздействий

Рис. 2. Выгибы элементов ферм из-за изменения расчетной схемы

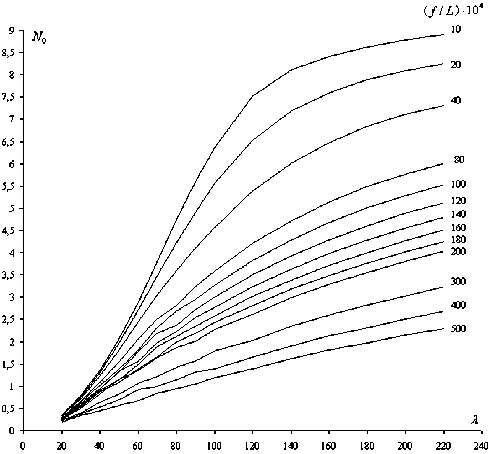
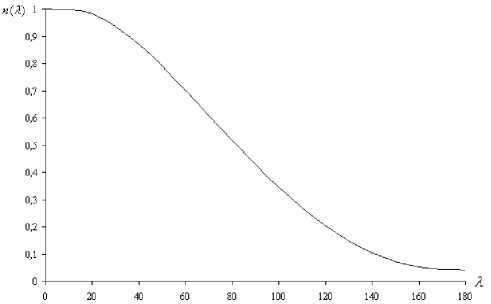
Расчет центрально сжатых стержней при проектировании производится сравнением действующего напряжения М(дТ) с расчетным сопротивлением по пределу текучести по известной формуле a-N/(oA)

Существуют методики [3; 7-8], в которых значение коэффициента продольного изгиба ц определяется с учетом различных типов сечений и с учетом произвольной начальной деформации стержня. Общий вид зависимости о от погибиf/L, гибкости X и отношения модуля Юнга

Рис. 3. Графики зависимостейу/р и Д1/2/р от гибкости X: 1 - из плоскости ферм; 2 - в плоскости ферм, в сторону стенки; 2 - в плоскости ферм, в сторону полки к расчетному пределу текучести Ry/E, может быть записан в виде

Ф = N0 KcKR⁽E-)Л>

Ry λ где N0 - безразмерная критическая сила, рассчитанная для стержня прямоугольного сечения с начальной поги-бью по дуге окружности и предела текучести, равного R1 = 206 МПа (зависящее от относительной погиби и гибкости стержня); Кс, KR - поправочные коэффициенты, учитывающие сечение, отличное от прямоугольного и предел текучести, отличный от эталонного значения. Коэффициент К равен 1 для прямоугольного (базового) сечения, для прочих типов сечений он корректируется в зависимости от гибкости стержня.

Значение безразмерной критической силы N₀ для зна-чений//Г в диапазоне от 0,001 до 0,05 было найдено серией численных расчетов по методу конечного элемента (МКЭ). Расчеты проводились с учетом геометрической нелинейности сжато-изогнутого стержня и упругопластических свойств стали в программе CalculiX 1.7, распространяемой по лицензии GNU General Public License. Искомое значение критической силы принималось равным максимальной несущей способности, по точке на графике «сила-перемещение», в которой расчетная кривая становится практически параллельной оси абсцисс, т. е. дальнейшая деформация балки происходит без значительного увеличения нагрузки.

Для аппроксимации диаграммы деформирования стали при выполнении физически нелинейных расчетов, использовалась принятая в машиностроительных расчетах степенная зависимость между истинными напряжениями у и логарифмическими деформациями е:

а = аТ (e / eT) m при e > eT = or/E, где m и аТ соответственно равны ln[os (1 + 1,4V, /100)/ o0,2]

^m = 0,⁷⁵--------i----------ioT"

ln[-------₂--------In -⁰⁰— ] 0,2-10^-2+o₀,₂/E 100 -v _f

[----------^2-----------]^1/(1-m>

^T    (0,2-10^-2E + o₀,₂)^m

Здесь использованы общепринятые обозначения стандартных характеристик механических свойств, получаемых при испытании на растяжение: E - модуль Юнга, о_{0 2} - условный предел текучести, <з_в - предел прочности, 1^ - сужение образца в шейке, %.

Значения коэффициентов уравнений регрессии

График зависимости N_Q от гибкости X и различных значений относительных искривлений//X приведен на рис. 4. Кривые, соответствующие//X в диапазоне от 0,001 до 0,05, возрастают при увеличении гибкости, оставаясь не больше максимального теоретического значения, равного п².

Значение коэффициента K_R представляется формулой KR = (Ry / R1)^n(λ).

Зависимость показателя степени от гибкости элемента получена аппроксимацией значений, полученных численно по МКЭ:

n(X) = -2,18 ■ 10^-9X⁴+1,20 ■ 10^-6X3 - 0,000189 X²+ 0,002 52 X +1.

График зависимости показателя степени n(X) показан на рис. 5. При моделировании рассматривались значения R^ для малоуглеродистых и низколегированных сталей, используемых в строительных конструкциях и машинах, класса прочности до С 590.

Методом статистических испытаний (Монте-Карло) исследовалась случайная величина, равная разности действующего в элементе усилия и предельного усилия по условию устойчивости. Распределение действующих осевых усилий и предела текучести стали принималось по нормальному закону. Для генерирования значений случайных эксцентриситетов использовались описанные выше распределения с параметрами, найденными в результате статистической обработки данных по методу моментов. Предельное усилие вычислялось по общей методике, приведенной выше.

По результатам моделирования, для разности предельного и действующего усилий, характеризующей надежность элемента, гипотеза о распределении по нормальному закону не отвергается критерием -^2 при уровне значимости 0,05.

Рис. 4. Графики зависимости N₀ от гибкости X и относительных искривлений//X

Рассмотренные статистические и аналитические зависимости могут быть использованы для выполнения проектных расчетов стержней на устойчивость по усовершенствованной методике, учитывающей возможность появления погнутостей, превышающих 1/750 дли ны стержня, с учетом типов сечений стержней и срока эксплуатации конструкций. В рамках дальнейших исследований предполагается привлечение дополнительных статистических данных, уточнение параметров распределений случайных величин, обобщение и доведение предлагаемого метода до компактного вида, удобного в инженерном использовании.

Рис. 5. График зависимости показателя степени п от гибкости X в формуле для поправочного коэффициента K_R