Оценка точности измерения термопреобразователей сопротивления в процессе работы

Одной из основных задач АСУ ТП является процесс измерения и обработки информации о физических величинах, характеризующих производственные технологические процессы [1–3].

Создание высокопроизводительного и высокоэффективного производства, обладающего возможностью быстрой переналадки при переходе с управления одного типа изделия на другой [4, 5], необходимо для своевременных обоснованных принятий решения в сложных и взаимосвязанных процессах. В таких условиях производства многократно повышаются требования к достоверности измерительной информации. Это, в свою очередь, стало возможно с появлением интеллектуальных средств измерений.

Под интеллектуальными средствами измерения мы будем понимать средства измерения с функцией самоконтроля согласно ГОСТу [6]. Оценка состояния средств измерения в процессе работы позволяет повысить достоверность и точность измерения, увеличить межповерочный интервал [6–8], повысить качество функционирования АСУ ТП в целом.

В настоящее время в современных средствах измерения имеется существенный незадейство-ванный резерв производительности встроенных микропроцессоров. Наиболее актуальной задачей использования этих вычислительных резервов для дальнейшего совершенствования средств измерений принято считать поиск новых вариантов создания интеллектуальных средств измерения [9–12].

Работы [13–24] касаются проблем самостоятельной оценки достоверности результатов измерения температуры в процессе эксплуатации. В приведенных источниках рассматриваются подходы и предлагаются варианты измерительных преобразователей и алгоритмы их работы. Возможности самодиагностики таких измерительных преобразователей предлагается реализовать, исходя из физических взаимосвязей измеряемых величин. Однако в этих работах недостаточно освещены вопросы качественной оценки точности измерения и самостоятельной качественной оценки состояния средств измерения в процессе функционирования.

Актуальность проблем создания интеллектуальных средств измерения подтверждается большим количеством статей и введения ГОСТов [6–8] по данной тематике.

Целью настоящего исследования является создание алгоритма оценки точности измерений, присвоения статусов состояния термопреобразователей сопротивления.

1. Схемы интеллектуальных измерителей температурына основе металлических сопротивлений

В предыдущих работах автора [25, 26] были исследованы две интеллектуальные схемы измерения температуры на основе термосопротивлений.

На рис. 1 изображена схема термометра термосопротивлений без опорного сопротивления.

Температуру можно вычислить двумя различными способами (1), (2). Температуру, измеренную первым способом, обозначим как T 1, температуру, измеренную вторым способом, как T 2:

X ( T 1) = ^{R тч1 ( T 1)};

R тч2 ( T 1)

Y ( T 2) =Δ ^{U н} = ^I ⋅Δ ^{R н}

Δ U п I ⋅Δ R п

Δ R н

Δ R н = Δ T ≈ R н ( T 2) | T 2 .

Δ R п    Δ R п    R п ′ ( T 2) | T 2

Δ T

Параметр оценки состояния d можно рассчитать формуле d=T2n-T1n+2T1n-1,

по

где n – текущее измерение, а n – 1 – предыдущее измерение.

Фактически параметр d является разницей двух измеренных разными способами температур единого процесса, характеризуя абсолютные погрешности этих измерений.

Исследования показали целесообразность усовершенствования параметра оценки состояния d , используя данные по диапазону измерений. Для этого можно использовать усреднение по диапазону | d ср |:

n

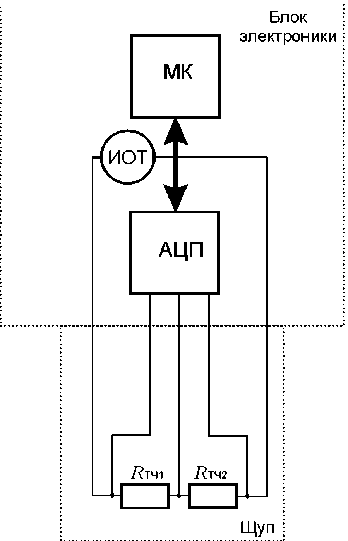
Рис. 1. Схема интеллектуального термометра сопротивления без опорного сопротивления

d ср ⁼

∑ ^d I i =1

n

.

Перспективным способом усовершенствования методов оценки состояния средства измерения является метод регуляризации. В работах [27, 28] был получен критерий Δ , определяемый выражением max Δk Δ , maxабс. погр k который также будем рассматривать как критерий оценки исправности средства измерения в некотором диапазоне измерений. Здесь max Δk – максимальное по модулю значение Δ в диапазо-k не измерений, maxабс. погр – максимальная допустимая абсолютная погрешность в диапазоне k измерений, k – набор отсчетов.

Параметр Δ _k здесь также фактически является разницей двух измеренных разными способами температур единого процесса, характеризуя абсолютные погрешности этих измерений.

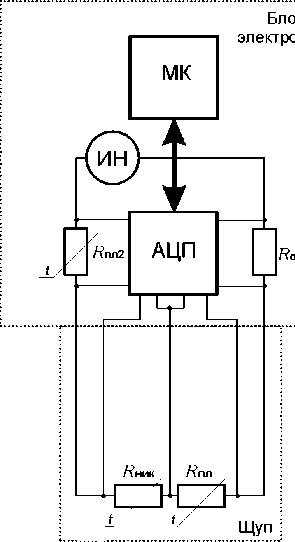
Рис. 2. Интеллектуальная схема термометра сопротивления с двумя измерительными преобразователями из различных металлов

Таким образом, для рассмотренной схемы получены 2 независимых критерия оценки ее состояния.

На рис. 2 изображена схема без опорного сопротивления.

Температуру можно вычислить двумя различными способами (5), (6). Температуру, измеренную первым способом, обозначим как T 1, температуру, измеренную вторым способом, как T 2:

R = R 41 ( T 1);

R = R .2 ( T 2).

Параметр оценки состояния d можно рассчитать по формуле

d = T 2 - T 1.

Параметры | d ср | и Δ для данной схемы измерения рассчитываются аналогично, из выражений (4) и (5).

Здесь d и A k , как и в предыдущей рассмотренной схеме, также фактически являются характеризациями абсолютных погрешностей измерений.

Из предыдущих исследований был получен алгоритм расчета порогового критерия для выхода измерителя температуры за допустимые пределы для обоих параметров – | d ср | пор и Δ пор . При | d ср | > | d ср | пор или |Δ| > Δ пор принимается решение о выходе преобразователя температуры за пределы допустимой погрешности.

Так и м об ра зом, для ра с смотре н н ой с хе мы так ж е п олучены 2 независимых критерия оценки ее состояния.

• 2.    Метод оценки состояния с помощью параметра Dи результаты измерений для предложенных схем

При в е д ен ны й в ыш е к ри т е ри й d основан на усреднении полученных оценок в диапазоне измере н ий , п оэ тому с е го помощью наиболее достоверными оказываются оц ен к и с и с те ма ти чес к о й п огреш н ости изме р е н и й . При в е д е н н ый в ыш е к р и те ри й Δ основан на экстремальных оценках ди а п а зон а и зм ере н и й , с о ответс твенно, с его помощью наиболее достоверно оц е н и в а ю тс я отд е л ьн ы е н а и б оль ш и е п огр е шн ос ти диапазона измерений. Для более точного пр и н яти я ре ш е н и я о вых од е и зме ри т е льн о го п реоб ра зов а те ля те мп е р а ту ры за пределы допустимой погрешности предлаг а е тс я о б ъ е д и н и ть о б а кр и те ри я в ед и н ый критери й D :

¹      I d ср|     ,1      l^Al

D =           + .

• ² I d ср. по р |     ² |^А пор |

При ме н и м п олу че н н ые кри те ри и д ля п ри с в о е н и я статусов результатам измерений.

ГОСТы [6–8] определяют статусы измерений, рассмотрим основные из них: подтвержденн ы й , н орма льн ый , орие нти ру ющий, недостоверный. Алгоритмы расчета гра н и чн ых поро гов ых значений | d _ср | и Δ межд у с та ту сами измерения для обеих рассматриваемых с хе м н а ос н ов е м е тодов и м и та ц и он н ого мод ели ров а н и я б ы ли рассмотрены автором данной статьи в [25], результаты п ри в е де н ы в таб л. 1 и 2. Т ам же приведены пороговые значения и для статус а D .

Таблица 1 Соответствие оценки критериев d _{ср. пор} и Δ для схемы без опорного сопротивления

Статус измерений	| d ср. пор |, °С	|Δ пор |	D
Подтвержденный	< 0,023	< 0,035	< 0,49
Нормальный	0,023…0,0467	0,035…0,71	0,49…1
Ориентирующий	0,0467…0,093	0,071…0,176	1…2,23
Недостоверный	> 0,093	> 0,176	> 2,23

Таблица 2

Соответствие оценки критериев d _{ср. пор} и Δ для схемы с двумя термопреобразователями из различных металлов

Статус измерений	| d ср. пор |, °С	|Δ пор |	D
Подтвержденный	< 0,101	< 0,104	< 0,46
Нормальный	0,101…0,196	0,104…0,257	0,46…1
Ориентирующий	0,196…0,262	0,257…0,501	1…1,64
Недостоверный	> 0,262	> 0,501	> 1,64

Далее рассмотрим результаты экспериментальной оценки.

• 3.    Результаты экспериментальной оценки точности исследуемых измерительных преобразователей

  • 3.1.    Результаты экспериментальной оценки точности исследуемых измерительных преобразователей для схемы с двумя первичными преобразователями из различных металлов

Абсолютные и допустимые погрешности первичных преобразователей температуры для схемы с двумя первичными преобразователями из различных металлов с помощью объединяющего два разных метода параметра D представлены на рис. 3–5. Границы статусов промаркированы: границы статусов подтвержденный – нормальный (η = 0,5) – кружками, нормальный – ориентирующий (η = 1) – ромбами, ориентирующий – недостоверный (η = 2) – треугольниками.

Изображенная на рис. 3 оценка исправности характерна для средства измерения, находящегося в начале межповерочного интервала. Состояние средства измерения соответствует границе статусов подтвержденный – нормальный .

Изображенная на рис. 4 оценка исправности характерна для средства измерения, незначительно превысившего свой межповерочный интервал, что соответствует границе статусов нормальный – ориентирующий .

Изображенная на рис. 5 оценка исправности характерна для средства измерения, существенно превысившего свой межповерочный интервал. Данная ситуация соответствует границе статусов ориентирующий – недостоверный .

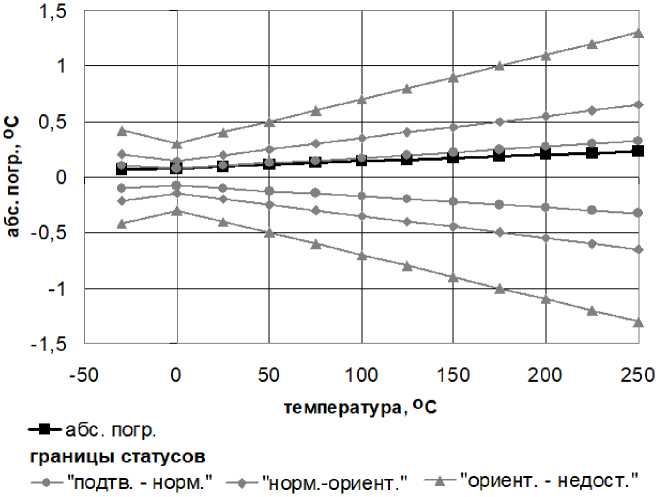
Рис. 3. Абсолютные и допустимые погрешности первичных преобразователей температуры для схемы с двумя первичными преобразователями из различных металлов. D = 0,454

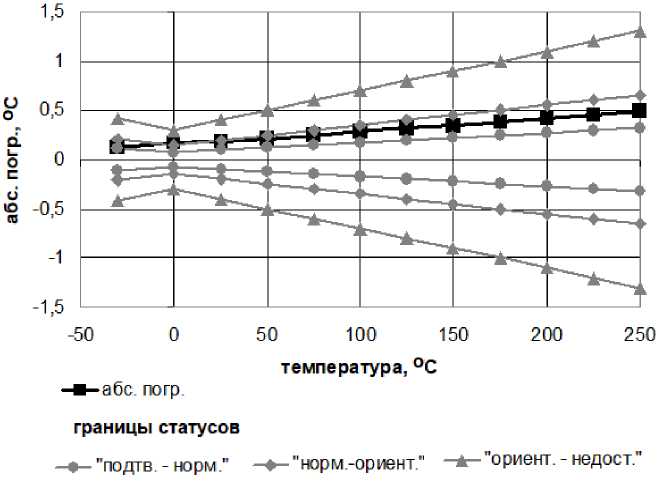
Рис. 4. Абсолютные и допустимые погрешности первичных преобразователей температуры для схемы с двумя первичными преобразователями из различных металлов. D = 0,997

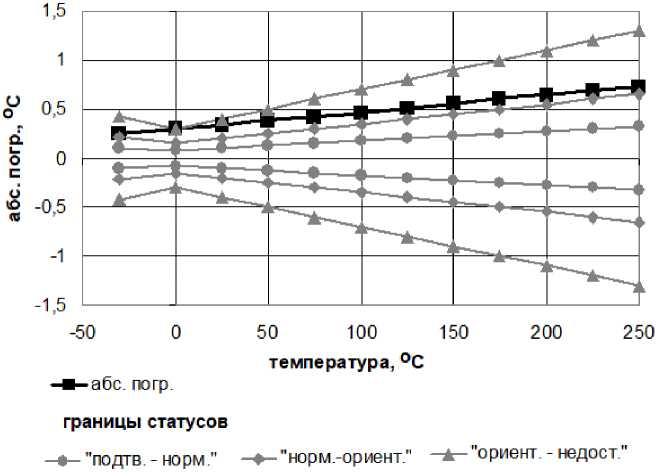
Рис. 5. Абсолютные и допустимые погрешности первичных преобразователей температуры для схемы с двумя первичными преобразователями из различных металлов. D = 1,621

Как видно из приведенных графиков, для схемы с двумя первичными преобразователями из различных металлов предложенный алгоритм оценки погрешности показал адекватность своей работы.

• 3.2.    Результаты экспериментальной оценки точности исследуемых измерительных преобразователей для схемы с двумя первичными преобразователями для схемы без опорного сопротивления

Далее рассмотрим абсолютные и допустимые погрешности первичных преобразователей температуры с помощью объединяющего два разных метода параметра D для схемы без опорного сопротивления. Они представлены на рис. 6–8. Границы статусов здесь промаркированы: гра- ницы статусов подтвержденный – нормальный (η = 0,5) – кружками, нормальный – ориентирующий (η = 1) – ромбами, ориентирующий – недостоверный (η = 2) – треугольниками.

Изображенная на рис. 6 оценка исправности характерна для средства измерения, находящегося в начале межповерочного интервала. Состояние средства измерения соответствует границе статусов подтвержденный – нормальный .

Изображенная на рис. 7 оценка исправности характерна для средства измерения, незначительно превысившего свой межповерочный интервал, что соответствует границе статусов нормальный – ориентирующий .

Изображенная на рис. 8 оценка исправности характерна для средства измерения, существенно превысившего свой межповерочный интервал. Данная ситуация соответствует границе статусов ориентирующий – недостоверный .

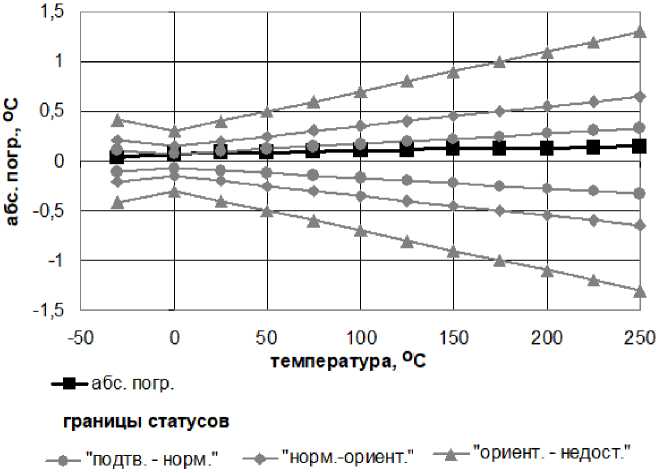
Рис. 6. Абсолютные и допустимые погрешности первичных преобразователей температуры для схемы без опорного сопротивления. D = 0,489

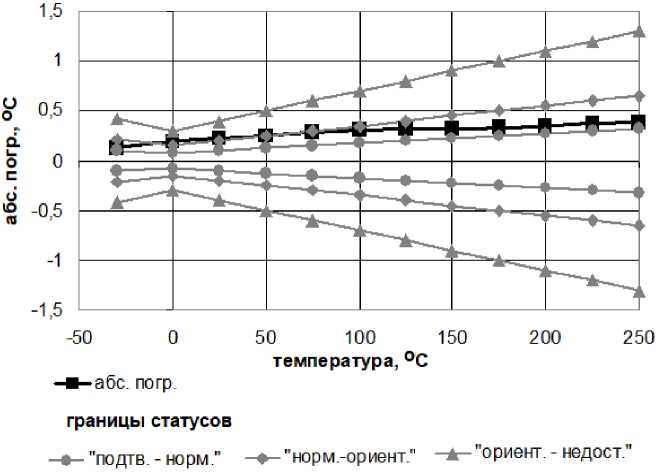
Рис. 7. Абсолютные и допустимые погрешности первичных преобразователей температуры для схемы без опорного сопротивления. D = 0,99

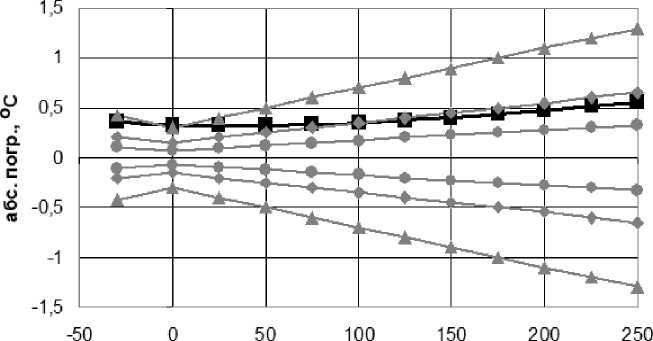
температура, °C

-■—абс. погр.

границы статусов

-е-"подгв. - норм " -*-"норм.-ориент." -*-"ориент. - недост"

Рис. 8. Абсолютные и допустимые погрешности первичных преобразователей температуры для схемы без опорного сопротивления. D = 2,224

Как видно из приведенных графиков, для схемы без опорного сопротивления предложенный алгоритм оценки погрешности также показал адекватность своей работы.

Заключение

• 1.    Рассмотрены две схемы измерительных преобразователей температуры на основе термосопротивлений: без опорного сопротивления и с двумя первичными преобразователями из различных металлов, обеспечивающие избыточность измерительной информации.

• 2.    Для обеих рассмотренных схем введен параметр оценки состояния D , характеризующий величину абсолютной погрешности измерения, сформированный на основе двух разных методов, на основе параметров d и Δ _k .

• 3.    Для обеих рассмотренных схем предложен алгоритм присвоения статусов состояния интеллектуальных измерительных преобразователей температуры на основе термосопротивлений.

• 4.    Экспериментальные исследования подтвердили эффективность предложенных в работе алгоритмов определения оценки исправности и присвоения статусов состояния для рассмотренных схем измерительных преобразователей.