Оценка точности методов трекинга для определения 2D-координат и скоростей механических систем по данным цифровой фотосъёмки

Экспериментальное исследование сложных механических систем связано с необходимостью использования нескольких датчиков координат и скоростей. Число датчиков пропорционально числу степеней свободы системы. Во многих системах затруднительно размещать датчики непосредственно на движущихся узлах системы. Сложность размещения датчиков и сбора информации с них значительно усложняет проведение натурных экспериментов. Использование бесконтактных оптических методов измерений существенно упрощает задачу.

Механические движения непосредственно наблюдаемы в оптическом диапазоне. Многие системы имеют достаточно высокие частоты (100 Гц и более). Как следствие, главную технологическую сложность при оптической регистрации движений представляет необходимость фотосъёмки с высокой частотой. В последние десятилетия на рынке появились камеры, способные осуществлять цифровую фотосъёмку с частотами до 1 млн кадров/с (производители Fastec, Photron, Vision Research). Развитие регистрирующей аппаратуры, с одной стороны, и методов трекинга объектов (раздел компьютерного видения) – с другой, открывают возможности для широкого использования оптических методов измерений в экспериментальных исследованиях систем со сложной кинематикой.

Трекинг объектов (object tracking) – активно развивающееся направление компьютерного видения [1]. Имеется большое число различных методик отслеживания объектов на серии изображений, однако большинство из них непригодны для использования в точном натурном эксперименте. В основных приложениях компьютерного видения, таких как охранное видеонаблюдение, анализ транспортного потока [2], транс- ляции спортивных событий (получение статистик по скоростям полёта снаряда, скоростям и общей дистанции, пройденной спортсменом в игровых видах спорта) [3], распознавание жестов и т.п., как правило, не требуется высокой точности в определении координаты. Методы, главным образом, направлены на решение множества смежных задач – выделение объекта от динамического фона в условиях переменного освещения [4], повышение качества изображений [5], обработка данных в режиме реального времени.

Натурный физический эксперимент, с одной стороны, предъявляет повышенные требования к точности определения координат объектов, с другой стороны, в эксперименте можно обеспечить регистрацию более качественных изображений и постоянство освещения. Также можно разными способами маркировать сам объект. Это позволяет избежать дополнительной обработки изображений и сосредоточить усилия на главной задаче – точном определении координат. В связи с этим исследователи начали заниматься адаптацией существующих методов компьютерного видения к натурным механическим экспериментам, а также разработкой новых методик. Кроме того, на рынке появился ряд программно-аппаратных комплексов для решения задач трекинга в лабораторных условиях для широкого круга приложений: спортивная биомеханика, компьютерная анимация, баллистика и др.

На текущий момент в литературе отсутствуют полноценные сведения о возможностях и ограничениях существующих методик трекинга для обработки данных механических экспериментов. Недостаточно исследована точность идентификации координат и скоростей. Целями работы являются сравнительный обзор и анализ эффективности применения существующих методик трекинга для идентификации координат и скоростей объектов в механических лабора- торных экспериментах. Исследуется точность измерения координат и скоростей объектов в модельных натурных механических экспериментах. В работе рассматриваются также специализированные методы идентификации координат, разработанные автором ранее для применения в экспериментальных исследованиях механических систем, обладающие повышенной точностью и устойчивостью к изменению условий освещения.

Рассмотренные в статье методы идентификации 2D-координат могут быть расширены на случай идентификации 3D-координат путём использования нескольких калиброванных камер (система стереозрения) [6]. Тестирование методов происходило на компьютере с параметрами – 3 ГБ ОЗУ, Intel Pentium® 3,74 ГГц. Далее для краткости будем называть этот компьютер «тестовым».

К вопросу о применимости оптических методов

При использовании фотосъёмки для определения координат и скоростей механических систем основную роль в точности измерений играют параметры цифровой фотокамеры. Пространственное разрешение большинства скоростных камер (производители Fastec, Photron, Vision Research) составляет более 1 Мпикс. Если нужно регистрировать относительно медленные движения, то можно воспользоваться обычными (не скоростными) видеокамерами с частотой съёмки до 60 кадров/c и с разрешением 8 Мпикс (например, Sony FDR AX1 4K [7]).

Пусть характерный размер объектов и/или перемещений составляет S , тогда при максимальном разрешении в 1 Мпикс можно добиться предельной (при максимальном увеличении камеры) точности измерения координаты до 10^–3 S . Далее в статье будет показано, что путём использования специализированных методов трекинга можно добиться субпиксельной точности (до нескольких сотых долей пикселя), таким образом, разрешающая способность может быть увеличена до 10^–5 S . При съёмке объектов размером 1 м можно достигнуть предельной точности в измерении координаты до нескольких сотых долей миллиметра.

Однако стоит отметить, что точность в определении координаты связана не только с размером матрицы фотокамеры, но и с конечностью времени выдержки. Ниже приведена методика оценки данной погрешности. Пусть A T - время выдержки камеры, V - характерная скорость движений объекта. Таким образом, за время, пока открыт затвор, объект пройдёт расстояние, равное V A T . Интервал времени между кадрами составляет 1/ f , где f – частота кадров. За время между двумя кадрами объект пройдёт расстояние V / f . За счёт того, что время выдержки не равно 0, объект на кадре будет смазан, что приведёт к ошибке в определении координаты. Среднее значение отклонения истинного значения координаты от измеренного составит V A T /2 (половина расстояния, проходимого объектом за время выдержки). Относительная ошибка в определении координаты составит

• V    A T /(2 X ), (1)

где X – истинное значение координаты.

Как видим, для уменьшения погрешности в определении координаты нужно уменьшать время выдержки. Использование малых времен выдержки может потребовать увеличения освещённости фотографируемой сцены. Для этой цели в лабораторных условиях используются источники постоянного освещения или стробоскоп, синхронизированный с камерой.

Максимальная ошибка определения смещения по двум кадрам составит V A T , таким образом, относительная ошибка определения смещения составляет A Tf Соответственно, относительная ошибка определения скорости по экспериментальным данным методом конечных разностей будет равна относительной ошибке в определении смещения. Стоит отметить, что время выдержки и частота кадров не являются независимыми параметрами – время выдержки не может быть больше интервала времени между кадрами, т.е.

A T = а / f , (2)

где а - положительное число, меньшее 1. Получаем, что относительная ошибка в определении скорости равна а . Подставляя (2) в (1), получаем

• V    а f /(2 X ). (3)

Увеличение частоты кадров приводит к уменьшению погрешности в определении координаты. В оценках погрешности мы не учитывали наличие ускорений, т.е. условно считали скорость постоянной. В реальных системах, как правило, скорость непостоянна. Поэтому для того, чтобы измерить скорость, надо брать такую частоту кадров, при которой изменением скорости за интервал времени между кадрами можно пренебречь, т.е.

A /( fV ) <<  1, (4) где A – характерное ускорение.

Методы трекинга объектов на изображении

Автор предлагает методы трекинга разделить на две категории – точечные и объектные. Первая группа методов основана на анализе отдельных пикселей или групп пикселей (прямоугольные, круглые области) на изображениях, полученных в ходе эксперимента. Методы второй группы основаны на выделении на изображениях сложных объектов с распределённой геометрией и последующем анализе самих объектов.

Данные методы требуют использования значительно более сложных алгоритмов обработки изображений, а также привлечения методов распознавания образов [8]. В работе [1] предложена схожая классификация, основанная на различном представлении объекта: точечные методы; методы, основанные на представлении объекта набором простых геометрических форм (круги, эллипсы, прямоугольники и т.п.); методы, основанные на отслеживании контура или силуэта объекта.

Суть точечных методов заключается в том, что на первом кадре вручную выделяется группа точек, положения которых нужно отслеживать в ходе эксперимента. Отследить точку в реальном эксперименте практически невозможно (на одиночном кадре присутствует множество точек со схожими яркостями и цветами). Поэтому вокруг каждой точки выделяется окрестность, состоящая из нескольких точек. Наиболее простой для реализации формой окрестности является квадратное окно с нечётным количеством пикселей с центром в исходной точке. Задача трекинга заключается в поиске наиболее похожих окрестностей на паре изображений. По сути, методика точечного трекинга сводится к задаче оптимизации функции похожести сегментов. Для этой цели можно применять различные методы: стохастическая оптимизация, градиентный спуск и другие [9]. Если учесть конечность перемещения объекта за время между двумя соседними кадрами, то зачастую проще реализовать полный перебор в прямоугольном окне, заведомо большем характерного смещения объекта.

Существуют различные подходы к поиску наиболее похожих областей, один из наиболее надёжных методов – метод сегментной кросс-корреляции. Данный метод зарекомендовал себя в PIV ( Particle Image Velocimetry ) [10] измерениях полей скорости в жидкостях, которые основаны на добавлении в поток светорассеивающих частиц и отслеживании их смещений по данным цифровой фотосъёмки. Критерием похожести служит максимальность следующего коэффициента коррел яции:

NN r=|E fs |/А E f 2 sb (5) V i=1 7 i=1

где F i , S i – яркости соответствующих пикселей сегментов на первом и втором изображениях, N – число пикселей на прямоугольном сегменте. Смещение сегмента, которому соответствует максимальная корреляция, определяет вектор смещения отслеживаемой точки объекта. Формула (5) справедлива для изображения в оттенках серого, но она легко обобщается на случай цветного из ображени я:

3 N 3 N

R = | E F i S i |/_A E F²S? , (6) V i =1 7 i =1

где под F , S будем понимать яркости RGB-компонент каждого пикселя. Если освещение сцены относительно постоянно, то можно использовать более простой критерий [11]:

3 N

R = E ( F - S i ) . (7) =1

Очевидно, что в случае использования малых окрестностей метод может оказаться неустойчивым к шумам изображения и перемене освещения. Кроме того, максимальная точность данного метода составляет 1 пиксель.

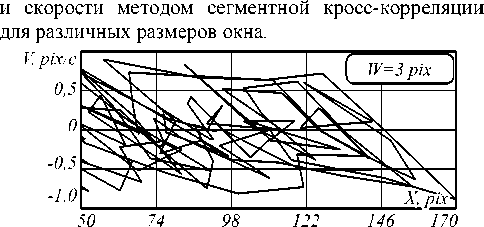
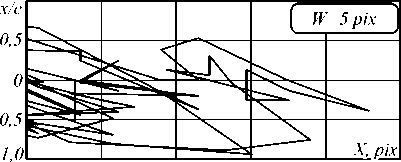
Для анализа метода сегментной кросс-корреляции был проведён эксперимент по определению координаты и скорости математического маятника. Маятник представлял собой шарообразное тело из пластилина, подвешенное на упругой нити, совершающее свободные колебания в поле тяжести. Съёмка движения осуществлялась цифровым фотоаппаратом Canon IXUS65 в режиме цифровой видеосъёмки с частотой 30 кадров/c. В качестве отслеживаемой точки был выбран центр шара. На рис. 1 представлены результаты (фазовые траектории) идентификации координаты

50     64      78      92     106   120

50    160     270     380     490   600

-1   X, pix

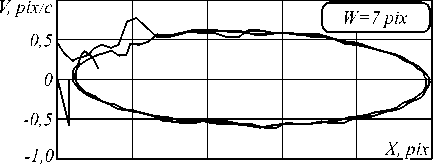
Рис. 1. Фазовые траектории математического маятника, идентифицированные методом сегментной кросс-корреляции при различных размерах квадратной окрестности W

Скорость определялась с помощью двухточечной конечной разности:

V = f ( X ₁₊ 1 - X . -1 ) /2,                             (8)

где X – измеренное значение координаты, – номер кадра, f – частота кадров.

Как видно, для малых окрестностей не удаётся идентифицировать координату (метод «путает» точки) и, соответственно, рассчитать скорость объекта. С ростом размеров окна растёт точность в определении координаты. Для квадратного сегмента со стороной 9 pix фазовая траектория принимает вид эллипса, что характерно для незатухающих свободных колебаний.

Приведём следующую оценку зависимости точности метода от размеров окна. Для этого зависимость координаты от времени была аппроксимирована методом наименьших квадратов (использовалась функция genfit пакета MathCad 14.0) теоретической зависимостью (свободные малые колебания):

X ( t ) = A cos ( to- 1 + ф ) + X_e .                       (9)

Ошибка метода оценивалась как ошибка аппроксимации:

N

К X - X ( i ) )

NA -----¹⁰⁰%,               (1°)

6 E =

где i – номер кадра, N – число кадров, X i – измеренное значение координаты. Аналогичным образом можно оценить ошибку в определении скорости. На рис. 2 показан график ошибки в зависимости от размера сегмента (при определении ошибки аппроксимации для явно ошибочных данных с W = 3, W = 5 использовалась теоретическая зависимость, определённая для W =9). Как видно из графиков, при превышении некоторого порога W (в нашем примере пороговое значение составило 7 pix) ошибка практически перестаёт падать и нет смысла использовать большее окно, т.к. это требует дополнительных вычислительных затрат.

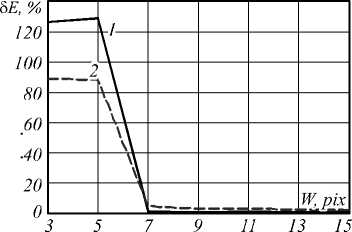
Рис. 2. Метод сегментной кросс-корреляции: зависимости относительной ошибки в определении координаты и скорости математического маятника от размеров квадратной окрестности W; 1 – ошибка определения координаты, 2 – ошибка определения скорости

Метод сегментной кросс-корреляции был реализован на языке C++, время обработки одного кадра размером 640×480 для W = 9 на «тестовом» компьютере составило 2700 мс. Вычислительная сложность алгоритма составляет O ( W ²MN ), где M×N – размеры изображения.

Помимо метода сегментной кросс-корреляции, существуют и другие методики, отличающиеся главным образом способом расчёта критерия похожести окрестностей отслеживаемых точек. Точечные методы применимы, когда вокруг отслеживаемой точки имеются перепады яркостных или цветовых характеристик изображения. Если пытаться отслеживать смещение точек равномерно окрашенного и освещённого объекта, то ошибка в определении координаты может равняться размеру объекта, т.к. метод будет путать отслеживаемую точку. Также желательно, чтобы на фоне не было точек, похожих на точки объекта, в противном случае ошибка может в разы превысить размеры объекта.

Как сказано во введении, существующие методы трекинга изначально ориентированы на отслеживание объектов в реальных (не лабораторных) условиях. Число объектов, их размер, форма, условия освещения, характер движений в общем случае считаются неизвестными. Наиболее часто подобные методы применяются в системах видеонаблюдения для определения характеристик движений объектов в охранной зоне [12].

В лабораторных же условиях, как правило, легко обеспечить постоянство освещения, также можно использовать однотонные фоны, размещаемые за движущимися объектами. Таким образом, часто удаётся легко выделить объект из фона. В отличие от точечных методов в данном случае объектом является некая группа точек – распределённый трассер, причём в объектных методах будет учитываться геометрия объекта: его размер и форма. Задача трекинга в данном случае состоит из нескольких этапов:

• 1)    детектирование (выделение) трассеров на паре кадров;

• 2)    идентификация одинаковых трассеров;

• 3)    детектирование (выделение) и идентификации пар характерных точек одинаковых трассеров;

• 4)    сопоставление смещений характерных точек трассера смещениям точек исследуемого объекта.

Рассмотрим этап детектирования трассеров. Существуют два подхода к выделению распределённых трассеров – силуэтный и контурный [1]. В силуэтных методах на кадре выделяется силуэт объекта. Простейший метод – это пороговый детектор. Считается, что пиксель принадлежит силуэту, если его яркость превышает некий порог (если объект ярче, чем фон, то предварительно можно взять негатив изображения). Пороговый и другие детекторы силуэта очень чувствительны к неравномерности освещения вдоль сцены и могут приводить к значительному искажению силуэта, поэтому контурным методам отдаётся предпочтение.

Контурные методы основаны на выделении на объекте с помощью детектора краёв резких перепадов яркости. В литературе существует большое количество алгоритмов выделения контуров [5]. Одним из наиболее эффективных методов является алгоритм Кэнни [13].

В качестве примера контурного метода рассмотрим разработанный автором в 2006 году метод [8]. Для выделения трассеров используется алгоритм Кэнни, для отыскания одинаковых трассеров вводится идентификационный критерий (критерий сходства или критерий различия). Сходство предлагается характеризовать схожестью формы и размеров, для описания которых нужны количественные характеристики. Пусть изначально контур представлен в виде упорядоченного множества N точек с координатами x i , y i , i = 1, 2, … , N , соответствующих контуру объекта. В работе [14] предложено каждому контуру ставить в соответствие трёхмерный вектор V , компоненты которого определяются следующим образом:

V = M 20 + M 02,(11)

V2 =(M20 - M02 )2 + 4M2,

V3 =(M30 - 3M12 )2 + (3M21 - M03 )2,(13)

где M pq – центральные моменты трассера;

1 ^N

Mpq =M^( xi- x ) p ( У-- y ) q ,

N i =1

где x , y – средние по множеству точек значения координат. Данное представление инвариантно относительно преобразований сдвига и поворота.

В качестве меры различий K используется евклидово расстояние между концами векторов U и V , соответствующих сравниваемым контурам. Компоненты векторного представления имеют разные порядки по координатам точек контура: первая компонента – второй порядок, вторая – четвёртый, третья – шестой. Наименьшее общее кратное составляет 12, поэтому при вычислении расстояния следует использовать формулу [8]

к = / U 1 - V 1 ) 6 + U 2 - V 2I ³ + ( U 3 - V 3 ) ² . (15)

Данный критерий был использован нами в работе [11] и показал хорошие результаты.

После того как на соседних кадрах были найдены контуры, соответствующие объекту, необходимо выделить на них характерные точки. Главной характерной точкой трассера считается его «центр-масс». Координаты «центра-масс» контура определяются как средние по множеству точек трассера значения координат. Смещение характерной точки сопоставляется со смещением объекта. Если объект совершает вращательное движение, то для описания его движения как движения твёрдого тела потребуется знать смещение ещё в нескольких точках объекта. Для детектирования дополнительных точек можно применить алгоритм, описанный в работе [15].

Благодаря использованию распределённого трассера контурный метод позволяет определять координаты объектов с субпиксельной точностью.

С одной стороны, поскольку цифровое изображение, регистрируемое фотокамерой, дискретно, получается, что точность в определении координаты не может превышать 1 pix. С другой стороны, ввиду того, что на фотографии идентифицируется не точка, а контур, имеющий распределённую геометрию, точность повышается до долей pix. Пусть контур метки смещается на расстояние менее чем 1 pix, например, на расстояние 0,5 pix вправо. Ввиду дискретности изображения часть точек контура неизбежно сместится на один пиксель (рис. 3), что позволит определить смещение контура.

Описанный выше контурный метод был применён для идентификации координат математического маятника (рис. 4).

Видно, что из-за слабого перепада яркости в правом верхнем углу образовался разрыв контура, одна- ко это не помешало успешно идентифицировать фазовую траекторию маятника (рис. 5).

Рис. 3. К вопросу о субпиксельной точности: слева – начальное положение контура, справа – положение контура в следующий момент времени при его смещении вправо на 0,5 pix; серым цветом закрашены пиксели, которые заняты меткой более, чем наполовину

Рис. 4. Обработка фотографии математического маятника контурным методом: слева – исходное фото, справа – результат выделения контура метки методом Кэнни [13]; крестом показан центр контура, определённый путём усреднения координат

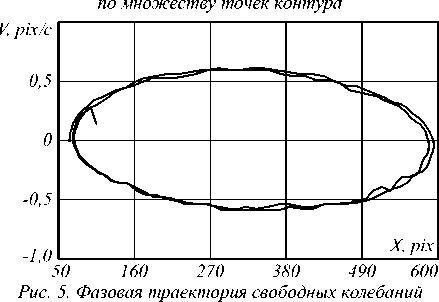
математического маятника, идентифицированная контурным методом

Ошибки аппроксимации зависимостей координаты и скорости от времени составили 1 % и 3,6 % соответственно. Контурный метод был реализован на языке C++, время обработки одного кадра размером 640×480 на «тестовом» компьютере составило 140 мс. Вычислительную сложность контурного метода можно оценить по наиболее ресурсоёмкому шагу – выделению контуров с помощью алгоритма Кэнни, которая имеет порядок O ( MN ), где M×N – размер изображения.

Контурный метод более стабилен, чем метод сегментной кросс-корреляции, и применим даже тогда, когда исходный объект однородно окрашен и освещён. Стоит отметить, что если на самом объекте имеются значительные перепады яркости, то это мо- жет приводить к значительному искажению формы контура объекта и неверной идентификации координат и скоростей. Упростить трекинг объекта позволяет закрепление на нём контрастных меток, имеющих заданный размер и форму. Чаще всего используются круглые или эллиптические метки, представляющие собой белый круг (эллипс) на чёрном фоне. Это существенно снижает вероятность искажения формы контура. Задача трекинга в данном случае состоит в отслеживании центров данных меток. Для идентификации на изображении фигур заданной геометрии существуют различные подходы. Один из наиболее популярных и быстрых алгоритмов – преобразование Хафа (Hough Transform) [16, 17].

Преобразование Хафа успешно применяется в различных приложениях компьютерного видения: видеонаблюдение, дефектоскопия [18], медицина [19] и др. Основная идея преобразования Хафа состоит в выделении на изображении с предварительно подчёркнутыми границами (контурами) (градиентное изображение) аналитических кривых, наиболее точно описывающих данные границы.

Для обсуждения логики метода Хафа рассмотрим пример выделения прямых линий на изображении. В полярной системе координат уравнение прямой имеет вид:

X cos ф + Y sin ф = R , (16)

где R , ф - неизвестные параметры [20]. Далее производится дискретизация пространства параметров R , ф и формируется двумерный массив, именуемый аккумулятором A R , ф . Затем производится так называемая процедура голосования.

Для каждого пикселя градиентного изображения, яркость которого превосходит некий порог, происходит накопление значений аккумулятора.

A r ,ф = A r ,ф + 1. (17)

Накопление происходит, только если координаты пикселя удовлетворяют уравнению (16) в рамках шага дискретизации в пространстве параметров.

Осуществляется поиск локальных максимумов в пространстве аккумулятора. Максимумы, набравшие число голосов больше порогового, соответствуют искомым прямым. Подобным образом преобразование Хафа может быть использовано для нахождения любых других аналитических кривых, в частности, окружностей:

( X - X c ) 2 + ( Y - Y c ) 2 = R ², (18)

где X C , Y C – координаты центра, R – радиус окружностей. В пространстве параметров ( X C , Y C , R ) используется целый шаг дискретизации, в противном случае метод потребует больших вычислительных затрат. Поэтому методика трекинга круглых меток, основанная на преобразовании Хафа, обладает точностью в 1 pix. Даже в случае использования дробного шага дискретизации точность метода будет ограничена шагом дискретизации по параметрам X C , Y C .

Предложенная методика была протестирована на идентификации свободных затухающих колебаний физического маятника, представляющего собой стержень, закреплённый на горизонтальной оси, совершающий малые затухающие колебания в поле тяжести (для демпфирования нижний конец стержня погружался в сосуд с водой). На самом стержне закреп- лялась контрастная метка в виде плоского картонного диска. Съёмка процесса проводилась скоростной фотокамерой Basler WatchGuard A504kc при частоте 400 кадров/c (рис. 6). Это требует установки малых времён выдержки, поэтому использовались дополнительные источники постоянного освещения Rekam HaloLight 1000.

Рис. 6. Фотография установки для исследования затухающих колебаний физического маятника

Программа для обработки кадров была реализована на языке C++ с помощью процедуры HoughCircles открытой библиотеки методов компьютерного видения OpenCV [21]. В данной процедуре использован модифицированный метод Хафа [22].

Вычислительную сложность данного метода можно представить в виде суммы

O ( MN ) + O ho„_gA . (19)

Первое слагаемое отвечает за этап выделения контуров, второе – собственно за модифицированное преобразование Хафа. С помощью модификации общего метода Хафа, которая подробно изложена в оригинальной работе профессора Роя Дэвиса [23], вычислительная сложность преобразования Хафа может быть сокращена до O ( E ), где E – число краевых точек (точек на градиентном изображении, яркость которых больше порога). Число точек в общем случае пропорционально линейным размерам изображения. Таким образом, можно пренебречь вторым слагаемом в (19), и итоговая вычислительная сложность составляет O ( MN ). Время обработки одного кадра размером 640×480 на «тестовом» компьютере составило 130 мс.

На рис. 7 приведён график зависимости скорости объекта от времени. Видно, что скорости идентифицировать не удалось, поскольку исследуемый объект совершает за интервал времени между двумя последовательными кадрами субпиксельные смещения. Ошибка аппроксимации зависимости координаты от времени теоретической кривой составила 2,8 %.

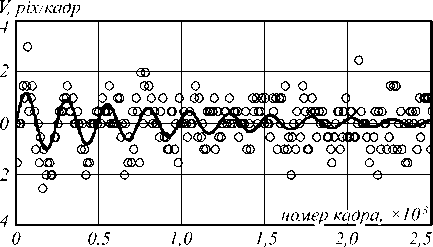
Рис. 7. Затухающие колебания физического маятника, идентифицированные методом Хафа: круги – эксперимент, сплошная линия – результат аппроксимации

В данном разделе был рассмотрен простейший метод Хафа для трекинга окружностей, не обладающий субпиксельной точностью. На сегодняшний день существует ряд расширений метода Хафа, обладающих субпиксельной точностью [24]. Стоит отметить, что для поиска кругов существуют альтернативные методы, например, основанные на преобразовании Радона, обладающие субпиксельной точностью [25].

Модифицированный контурный метод

Как показали эксперименты с физическим маятником, точность измерения координаты в один пиксель может оказаться недостаточной для определения скоростей механических объектов в случае, когда смещение объекта между двумя кадрами меньше пикселя. Из всех рассмотренных выше методов субпиксельной точностью обладает только предложенный автором контурный метод. Для повышения точности метода на объекте предлагается закрепить круглую или эллиптическую метку.

Однако контур метки может искажать свою форму вследствие изменения освещения, незначительного смазывания изображения из-за быстрого движения объекта; также на контуре может образовываться так называемая бахрома – дополнительные ответвления, вызванные наличием резких перепадов яркости на изображении метки. Кроме того, на одной из сторон контура метки могут появляться сдвоенные линии, что приведёт к увеличению числа точек в этой части границы и, как следствие, к ошибочному сдвигу центра метки, определяемому путём вычисления средних значений координат. Также на одной из сторон контура линия может претерпевать разрывы вследствие неверно заданных порогов по яркости в методе выделения контуров Кэнни или вследствие блика, попадающего на границу метки (рис. 8а). Все эти искажения могут приводить к невозможности определения скоростей объектов путём численного дифференцирования в натурных физических экспериментах. Для уменьшения данных ошибок автором предложен в 2007 году модифицированный метод, основанный на аппроксимации контура метки эллипсом [8]. Центр аппроксимирующего эллипса предлагается сопоставлять с центром метки. На рис. 8б показан контур метки и центры метки, определённые посредством усреднения и аппроксимации. Как видно, сдвоенность линий левой грани- цы привела к ошибочному сдвигу центра, определён- ного посредством усреднения.

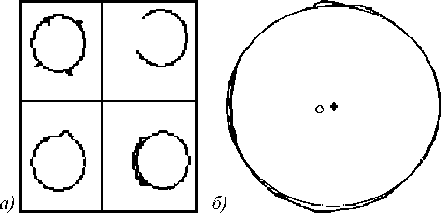
Рис. 8. Контуры метки: возможные искажения: слева-направо, сверху-вниз – бахрома, ложный разрыв, искажение формы, сдвоенность линий (а); определение центра метки: малый круг – усреднение по множеству точек, крест – аппроксимация эллипсом (б)

В литературе известны различные методы аппроксимации множества точек эллипсом или окружностью [26–28]. Для аппроксимации контура метки эллипсом предлагается простой в программной реализации метод, основанный на минимизации ошибки аппроксимации стохастическим итерационным алгоритмом, который описан в [29].

Модифицированный контурный метод был протестирован на серии фотографий процесса затухающих свободных колебаний (рис. 9).

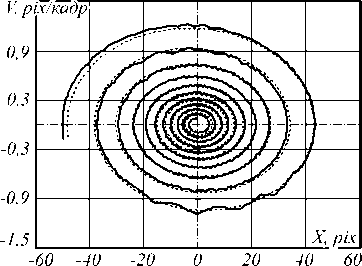
Рис. 9. Фазовая траектория затухающих колебаний физического маятника, идентифицированная модифицированным контурным методом: сплошная линия – эксперимент, пунктир – результат аппроксимации; ошибка аппроксимации 1,7 %

Напомним, что методом Хафа не удалось идентифицировать скорость маятника ввиду того, что за один кадр объект совершает субпиксельное перемещение.

Вычислительная сложность модифицированного контурного метода может быть представлена в виде

O ( MN ) + O ( EI ) ,                            (20)

где первое слагаемое отвечает за этап выделения контуров, второе – за аппроксимацию контура метки эллипсом. Во втором слагаемом E – число краевых точек, I – число итераций стохастического алгоритма.

Стоит отметить, что в большом числе случаев второе слагаемое может значительно превосходить первое, т.к. обычно используется не менее 3000 итераций [29], а размер контура по порядку равен линейному размеру изображения. Программа для модифицированного контурного метода была реализована на языке C++. Среднее время обработки одного кадра размером 640×480 на «тестовом» компьютере составило 5100 мс (использовалось 3000 итераций стохастического алгоритма).

Рассматриваемый метод был апробирован нами на серии экспериментальных задач: идентификация нелинейных [29] и вынужденных колебаний маятника, идентификация вынужденных колебаний связанных маятников [30], анализ движения и идентификация параметров натурной локомоторной модели [31]. Во всех экспериментах метод показал практически полную независимость от условий освещённости и субпиксельную (до нескольких сотых долей пикселя) точность в определении координат объектов.

Обзор программных продуктов

В последнее время на рынке появился ряд программно-аппаратных комплексов для решения задач трекинга в лабораторных условиях. В данном разделе представлен краткий обзор основных предлагаемых решений.

Большинство продуктов ориентированы главным образом на трекинг движений актёра с целью последующего создания анимированных 3D-моделей. Среди таких продуктов следует выделить решения фирмы Vicon [32]. Компания выпускает программные продукты Tracker, Blade, Nexus, позволяющие в режиме реального времени отслеживать координаты твёрдых тел по анализу данных с нескольких видеокамер. Решения компании применяются в таких отраслях, как киноиндустрия, спортивная и военная биомеханика. Данные продукты могут применяться и в других отраслях науки, в частности, в аэродинамике [33].

Существуют продукты, ориентированные преимущественно на научные исследования. Решение SwissTrack [34] является OpenSource-продуктом и предназначено для применения в роботехнике и био- механике. Среди коммерческих продуктов следует выделить решение TemaMotion [35] компании Image Systems. Данный продукт позволяет осуществлять все виды трекинга: точечный, контурный, силуэтный, трекинг объектов заданной формы, обладающий субпиксельной точностью. TemaMotion успешно применяется в таких отраслях, как автомобилестроение (проведение краш-тестов), спортивная биомеханика, военная промышленность (тесты стрелкового оружия) [36], а также в экспериментальной физике: например, в работе [37] приведено исследование процесса расширения металлического кольца под действием электромагнитного поля с использованием скоростной фотосъёмки и программного обеспечения компании Image Systems. Рассмотренные продукты могут применяться и в лабораторных исследованиях механических систем со сложной кинематикой: модели механизмов машин, локомоции биоподобных роботов, сложные колебательные системы и т.п.

Особо стоит отметить библиотеку OpenCV – opensource библиотеку с реализацией многочисленных методов компьютерного видения, которая успешно применяется исследователями при создании и тестировании собственных алгоритмов, в том числе систем трекинга. В частности, упомянутое выше решение SwissTrack использует функционал OpenCV. В случае, если разрабатывается программное решение для процессоров Intel, то можно использовать оптимизированные реализации некоторых базовых методов обработки изображений из коммерческой библиотеки Intell IPP [38]. В самой библиотеке OpenСv имеется возможность использования методов, основанных на использовании функционала Intell IPP.

Заключение

В табл. 1 приведены сравнительные характеристики рассмотренных в статье методик.

Табл. 1. Сравнительная характеристика методов

Метод	Тип метода	Устойчивость к изменению освещения	Точность измерения координаты (pix)	Вычислительная сложность обработки изображения размером M×N
СКК	Т	Низкая	1,00	O ( W 2 MN ), W – размер окрестности
К	О	Средняя	0,01	O ( MN )
МХ	О	Средняя	1,00	O ( MN )
МК	О	Высокая	0,01	O ( MN ) + O ( EI ), E – число точек контура, I – число итераций метода аппроксимации

Примечания: в табл. 1 обозначены: T – точечный метод, О – объектный метод, СКК – метод сегментной кросс-корреляции, К – контурный метод, МХ – модифицированный метод Хафа, МК – модифицированный контурный метод

Как видим, предлагаемый автором модифицированный контурный метод обладает самой высокой точностью, однако требует больших вычислительных затрат. Большой объём вычислений составляет этап аппроксимации множества точек эллипсом, соответственно, в будущем следует уделить внимание альтернативным методикам аппроксимации, вычислительная сложность которых может быть сокращена до O(E). В задачах, не требующих субпиксельной точности, можно применять модифицированное преобразование Хафа, а если размещение на объекте меток не- возможно, то точечные методы. Рассмотренные в статье методы легко обобщаются на случай исследования систем со многими степенями свободы. Для этого в точечных методах используется отслеживание нескольких точек, а в объектных методах применяются метки разного размера, формы и цвета.

Часто в реальных экспериментах перемещение объекта между двумя кадрами не превышает некоторого заранее известного порога. Поэтому вычислительная сложность многих алгоритмов может быть значительно сокращена. Особенно это относится к точечным ме- тодам, в них просто сужается область поиска похожих точек, для объектных методов это удаётся сделать не всегда, т.к. размер обрабатываемого сегмента на изображении не может быть меньше, чем трассер (контур объекта). В частности, в предложенных автором субпиксельных методах точность главным образом обусловлена большим числом точек контура.

Быстрое развитие методов компьютерного видения, различных регистрирующих устройств (скоростные фото-, видеокамеры видимого, ИК-, УФ-диапазона) открывают перспективы для их массового применения в научных экспериментах по анализу систем со сложной кинематикой.

Автор выражает благодарность доктору физ.-мат. наук, профессору М.А. Марценюку за ценные замечания по тексту статьи.