Оценка трещиностойкости сварных соединений с мягкими прослойками
Автор: Молоков К.А., Новиков В.В.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 4 т.21, 2021 года.
Бесплатный доступ
Введение. Рассмотрены сварные соединения в металлических крупногабаритных сооружениях (например, в конструкциях корпусов кораблей), подверженных малоцикловой усталости. Отмечено характерное для них появление мягких прослоек, которые при рабочих нагрузках значительно пластически деформируются. Деформация структуры металла с повреждениями, особенно в виде трещин, снижает прочность и надежность элементов конструкций и соединений. Предварительная деформация отрицательно влияет на пластичность, поэтому многое зависит от остаточной пластичности трескающегося материала. При этом с уменьшением остаточной пластичности снижается такой важный показатель надежности, как сопротивление материала распространению трещины - вязкость разрушения.Статья посвящена разработке модели, включающей аналитические зависимости для оценки трещиностойкости металлических конструкций и их сварных соединений с мягкими прослойками по пределу трещиностойкости при всех размерах трещин.Материалы и методы. Использованы теория и методы линейной механики разрушения материалов, структурно-механический подход. Результаты расчетов анализировались и сравнивались с экспериментальными данными и другими аналитическими решениями. Численный эксперимент выполнен для широко используемых в промышленности сталей феррито-перлитного класса Ст10, Ст50, 22К, Ст3сп и др., а также легированных закаленных на среднюю и высокую прочность 30ХГСА, 37ХН3А и др.Результаты исследования. Получены аналитические зависимости для расчета относительного предела трещиностойкости по трем основным известным механическим характеристикам материала мягкой прослойки сварного соединения.Обсуждение и заключение. Полученные результаты могут быть использованы для оценки трещиностойкости предварительно деформированных элементов конструкций и сварных соединений (в том числе с мягкими прослойками), работающих на поперечную нагрузку. Итоги экспериментальных данных и аналитических расчетов показаны в безразмерном виде, что позволяет получать инвариантные результаты по отношению к пределу трещиностойкости.
Сварное соединение, мягкая прослойка, механическая неоднородность, деформация, предел трещиностойкости, длина трещины, контактное упрочнение, относительное удлинение
Короткий адрес: https://sciup.org/142231891
IDR: 142231891 | УДК: 621.791.05:620.17 | DOI: 10.23947/2687-1653-2021-21-4-308-318
Текст научной статьи Оценка трещиностойкости сварных соединений с мягкими прослойками
УДК 621.791.05:620.17
Введение. В сварных соединениях, подверженных циклическим нагрузкам, часто возникают и развиваются трещины, которые могут стать причиной опасного состояния конструкций и их разрушения. В [1] приводятся примеры формирования таких трещин в корпусах судов. Кинетика образования в сварных швах макротрещин и их развитие зависят от множества факторов, что требует проведения комплексных исследований трещиностойкости сварных соединений и разработки соответствующих математических моделей.
На сопротивление металла распространению трещин существенно влияют появляющиеся после сварки так называемые мягкие прослойки, подверженные пластическому деформированию. Для разных участков сварного соединения характерна бо́льшая или меньшая степень неоднородности механических характеристик металла [2]. Она зависит от многих начальных условий технологического процесса. В их числе — скорость охлаждения зон сварного соединения и обработки свариваемой стали, а также содержание легирующих элементов, углерода и др. О. А. Бакши рассматривал некоторые проблемные вопросы вязкого и хрупкого разрушения механически неоднородных сварных соединений, влияния дефектов и микротрещин на процессы, происходящие в структуре металла при нагружении, и пр. Исследователи решили ряд частных задач по увеличению прочности и долговечности сварных соединений с прослойками [3–6].
Машиностроение и машиноведение
При установившемся режиме сварки ширина зон термического влияния (ЗТВ) и механические свойства металла незначительно меняются по длине сварного соединения. Поэтому целесообразно рассматривать неоднородность характеристик в разных зонах в сварном соединении при поперечной нагрузке. Для закаливающихся или прошедших термическую обработку (термоупрочненных) металлов характерно появление закалочных структур или разупрочненных зон соответственно. При этом в зависимости от свойств стали в исходном состоянии и параметров технологического процесса могут образовываться мягкие зоны. Здесь предел текучести σтм и предел прочности σвм металла меньше, чем в соседних прилегающих (так называемых твердых) областях σтт и σтв . Таким образом, мягкая зона будет вовлекаться в пластическое деформирование между областями с характеристиками σтт > σтм, σвт > σвм раньше соседних, а степень ее влияния на прочность соединения будет зависеть от схемы приложенной нагрузки1. Деформирование мягкой прослойки снижает сопротивляемость распространению трещины — инициируется интенсификация хрупкого разрушения, при котором критическая длина трещины уменьшится в разы [7].
Цель данного исследования — разработка аналитических зависимостей и математической модели для оценки трещиностойкости сварных соединений с мягкой прослойкой в результате ее предварительного пластического деформирования.
Допустим, что некоторое ограничение линейных размеров сварного образца (кроме толщины) под поперечной нагрузкой заметно не влияет на рассматриваемые в структуре металла процессы и явления (кроме образования мягкой прослойки), вызванные термическим циклом сварки.
Материалы и методы
Расчетные предпосылки. Рассмотрим изменение физико-механических характеристик металла мягкой прослойки при растяжении стыкового соединения поперек шва достаточно большой протяженности (рис. 1).
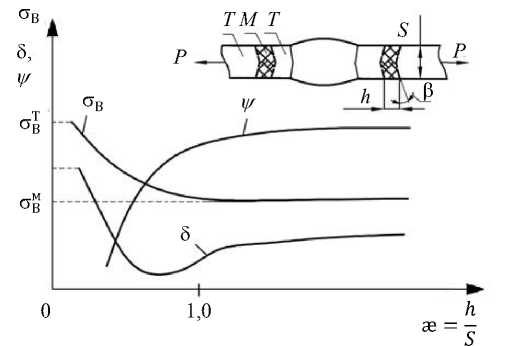
Рис. 1. Схема зависимости характеристик о в , б и ф от относительной толщины прослойки
В упругой стадии нагружения прослойка и соседние участки рассматриваемой области деформируются однородно. При достижении уровня напряжений, соответствующих пределу текучести о М , в ней образуется пластическая деформация, а соседние участки остаются в упругом состоянии. Для упрощения примем угол наклона грани прослойки в = 0 (рис. 1). При дальнейшем повышении нагрузки и деформации растет коэффициент поперечной деформации р (коэффициент Пуассона) мягкой прослойки. В итоге он будет больше, чем у соседнего участка металла. По мере развития пластической деформации в прослойке р ^ 0,5, а в областях с упругим состоянием металла р = 0,3. Из-за неодинаковой поперечной деформации в сварном шве возникают касательные напряжения. Максимальные их значения концентрируются в районе плоскостей раздела мягкой прослойки и соседних участков. Касательные напряжения препятствуют поперечному сужению мягкой прослойки в направлении толщины листа. Чем уже прослойка (т. е. чем меньше отношение ж = h/s , рис. 1), тем меньшее поперечное сужение она получает к моменту возникновения истинных разрушающих напряжений ор. Так возникает эффект контактного упрочнения, который обеспечивает повышение несущей способности.
Увеличение разрушающей силы имеет пределы. Соседние с мягкой прослойкой более прочные участки при определенных условиях тоже будут пластически деформироваться. Чем большей прочностью обладают соседние зоны и чем меньше относительная толщина прослойки ж, тем заметнее эффект контактного упрочнения. Его усиливают более твердые прослойки, находящиеся вблизи относительно мягких.
Относительное поперечное сужение ф в мягкой прослойке и абсолютное удлинение образца б зависят от ж и свойств металлов в соединении. В широких прослойках, когда еще нет контактного упрочнения, ф остается постоянным при уменьшении ж (рис. 1). А б постепенно падает по мере уменьшения ж в общей ширине сварного образца. В области контактного упрочнения ф резко уменьшается, так как растут поперечные касательные напряжения, препятствующие сужению прослоек в направлении толщины материала. Относительное удлинение образца б при этом также сначала уменьшается. Когда же реализуется существенная жесткость напряженного состояния в мягкой прослойке, б возрастает, поскольку в пластическую деформацию вовлекается металл твердой прослойки. Отметим, что при сварке термоупрочненных сталей бМ мягкой прослойки оказывается выше, чем б^. Но ее пластическая деформация значительно больше, и остаточная пластичность после нагружения до напряжений оМ > о > о“ может стать критической. В результате значительно уменьшается длина критической трещины, которая может возникнуть под действием дальнейших рабочих циклических напряжений на стыке мягкой и твердой прослоек. При этом существенно возрастает опасность хрупкого разрушения и следует оценить его возможность (предел трещиностойкости2,3 [8, 9]) в области с дефектом в виде трещины. При этом учитываются условия плоской деформации, контактного упрочения и пластически деформированной мягкой прослойки. По результатам исследования деформирования слоев композитного материала методом конечноэлементного моделирования [3] можно заметить, что наибольшая деформация мягкой прослойки образуется около стыка ее с твердой прослойкой. Особенно четко это проявляется при средних значениях относительной толщины прослойки ж.
Иногда при статической нагрузке удается найти оптимальное значение ж и достичь равнопрочности соединения. Однако имеющиеся в мягкой деформации могут развиться в трещины докритической деформации относительно деформации определяется по формуле2 [2]:
прослойке дефекты или несплошности после некоторой ее с критической длиной при условии, что оставшаяся часть мала. Степень контактного упрочнения в случае плоской
Кж
п +1 Ж
2V3 '
Временное сопротивление сварного соединения с мягкой прослойкой: о в с = о М ^К ж ,
где оМ — временное сопротивление мягкой прослойки.
Естественно, что для обеспечения равнопрочности при статической нагрузке требуется как минимум выполнение условия о™ = о ^ . В этом случае предельное (минимальное) значение коэффициента контактного упрочнения определяется отношением временных сопротивлений:
К жпред = о т / о м . (3)
Используя (1) и (2), найдем предельные значения жпред, при которых достигается равнопрочность соединения в условиях плоской деформации:
_ _ 1
Ж пре д = (2V3 К жпред - П)
Однако необходимо иметь в виду, что повышение прочности сварного соединения с мягкой прослойкой ограничивается истинными напряжениями отрыва для мягкого металла.
При сварке упрочненных сталей ширина разупрочненной зоны зависит от погонной энергии и регулируется выбором подходящего режима сварки. Для каждой толщины металла, способа и режима сварки есть определенная ширина разупрочненного участка, при которой обеспечиваются максимально возможное контактное упрочнение, а также равная прочность сварного соединения и основного металла.
Исследование участка разупрочнения при аргонодуговой и электронно-лучевой сварке металла толщиной 4,5–8 мм показывает:
-
— твердость на нем определяется только температурой нагрева;
-
— прочность соединений зависит не от уровня твердости разупрочненного участка, а от его ширины h (рис. 1).
При этом следует учитывать, что участок разупрочнения плавно переходит в более прочные участки зоны термического влияния.
Изучение кинетики и механизма разупрочнения в ЗТВ позволили установить, как на прочность сварных соединений влияют свойства участков, окружающих мягкую прослойку. Экспериментально обоснован новый критерий, определяющий временный предел прочности сварного соединения о вр , — это относительная ширина мягкой прослойки Ь 1 /Ь0. Предложенная эмпирическая зависимость имеет вид:
о в с = о М + 0,3о М (| ° ) + 0,3о М (| ° ) , (5)
Машиностроение и машиноведение
-
2 Матохин Г. В., Молоков К. А. Прочность и надежность сварных соединений. Владивосток : ДВФУ, 2019. 143 с.
-
3 Гольдштейн Р. В., Морозов Н. Ф. Механика деформируемого твердого тела: проблемы и результаты // Современные проблемы механики сплошной среды : всерос. конф. памяти академика Леонида Ивановича Седова в связи со столетием со дня его рождения. М. : Торус Пресс, 2009. С. 121–166.
где о ^р — предел прочности сварного соединения, МПа; оМ — предел прочности мягкой прослойки, МПа; Ьо — ширина прослойки при равной прочности сварного соединения и основного металла, м; Ь 1 — текущая ширина прослойки, м.
Из последнего уравнения следует, что при Ьо = Ь 1 мягкая прослойка упрочняется максимум на 60 %, т. е. о Т = 1,6о М , так как дальнейшее упрочнение не имеет смысла.
Результаты экспериментов указывают на снижение выносливости сварных соединений с мягкой прослойкой, образованной после сварки термоупрочненных сталей У4 и У6. Это говорит о существенном снижении несущей способности [10]. У этих сталей пределы выносливости сварных образцов без концентрации напряжений практически совпадают с пределами выносливости таких же образцов из неупрочненной стали. То есть, несмотря на термическое упрочнение сталей (способствующее повышению прочности), вибрационная прочность сварных соединений на базе 106 циклов оказывается практически одинаковой. Следовательно, можно предположить, что пластическая деформация в мягких прослойках вызывает раннее образование макротрещины, критический размер которой Lc резко ограничен происшедшими пластическими деформациями.
Трещиностойкость пластически деформированного материала мягкой прослойки до значений о < о М может оцениваться двухпараметрическим критерием разрушения — пределом трещиностойкости, который рассчитывается по известной аналитической зависимости 4 [2, 11]:
к =к4-®2- (6)
где ос — критическое напряжение разрушения в брутто-сечении; К1с — критический коэффициент интенсивности напряжений (постоянная материала мягкой прослойки).
После пластической деформации мягкой прослойки ос будет зависеть от характеристики дефекта. Примем, что эта характеристика — критическая длина Lc зародившейся трещины. Тогда ос = Kс/^пLс . Однако, чтобы воспользоваться (6), необходимо знать степень деформации прослойки, так как от нее в первую очередь будет зависеть Кс. Величину Lc будем считать неизвестной. Ее нужно определить в зависимости от деформации мягкой прослойки.
Авторы работ5 [11], исследуя структурный параметр разрушения d и определяя его для дисковидной трещины, приходят к выражению для оценки предела трещиностойкости в одномерном виде:
К ^ 72Л(1-П)
К1с arccos(n) '
где n = я/(я + d) — безразмерный параметр, заданный диапазоном изменения (0 < п < 1); я — радиус дисковидной трещины.
Из последнего равенства следует, что для больших трещин характерно относительно малое значение d,
-
а . Разрушение происходит с малыми пластическими деформациями в нетто-сечении, а Кс ~ К1с. Обратная ситуация складывается при относительно небольших трещинах, если для разрушения понадобится большая пластическая деформация в нетто-сечении, и п ~ 0, Кс « К1с.
Представим теперь, что мягкая прослойка подвергается циклической нагрузке. В этом случае
используем концепцию эффективного порогового коэффициента интенсивности напряжений К£ей06 для вычисления предельной амплитуды цикла нагружения о ^ г при уровне средних напряжений о М > от + о ^ г > о М . С этой целью рассчитаем длину начальной макротрещины L, соответствующей предельной амплитуде напряжений в пластически деформированном материале до от:
К^.
п о2г
1 - р + р2 о 2
)
пРи К№ 0 = Ка о ,т = -1,
где C j T — предельная амплитуда напряжений; а ^ с — циклический предел текучести; г — коэффициент асимметрии цикла; ц — коэффициент Пуассона.
Значение длины начальной макротрещины L следует подставить в расчетную зависимость для вычисления предела выносливости [12]:
[ -0,5
Ч^) "8 . (9)
Решением будут искомые значения предельных амплитуд. Характеристики, входящие в (9), вычисляются согласно [12] или 7 . Далее не составляет труда определить вклад предварительной пластической деформации мягкой прослойки в эквивалентную поврежденность с позиции оценки длины макротрещины.
Результаты исследования
Построение математической модели. Опишем предлагаемую последовательность разработки аналитических зависимостей. Оставшиеся пластические свойства элемента конструкции или ее части можно оценить по деформации, используя относительное удлинение для области материала. Будем считать, что на малом участке мягкой прослойки имеет место равномерная пластическая деформация. Она связана с критическим относительным удлинением до разрушения 65 ( 10 ) известной зависимостью [13]:
е = ln(1 + 65). (10)
Положим, что материал мягкой прослойки пластически деформируется. Рассмотрим случай, когда пластическое деформирование происходит только в первых циклах нагружения. То есть область мягкой прослойки вытягивается пластически под внешней поперечной номинальной нагрузкой, а далее она работает под упругими циклическими напряжениями. Так развивается усталостная трещина. В мягкой прослойке ее может спровоцировать высокая пластическая деформация и (или) дефект. Из-за снижения предельной деформации материала мягкой прослойки предварительное пластическое деформирование приводит к уменьшению критического раскрытия в вершине трещины. По результатам работы [14] можно заметить, что очень близка к линейной зависимость критического раскрытия вершины трещины 6С (КРТ) при деформации стали вытягиванием. Этот факт наблюдается как для алюминиевого сплава, так и для аустенитной стали. Итоги упомянутых экспериментов позволяют предположить, что при предельной равномерной пластической деформации этих материалов 6С = 0.
От степени предварительного деформирования существенно зависит предел выносливости. Такую зависимость сложно получить теоретически [15], потому что до области средней предварительной пластической деформации материала предел выносливости достигает минимума, а после возрастает и может достигать показателей как у недеформированного материала. Таким образом, сам факт появления трещины, видимо, играет основную роль в усталости. Нераспространяемые трещины даже при большой предварительной пластической деформации только в редких случаях ведут к разрушению. Это очевидно из примеров повреждений судовых конструкций, приведенных в [1].
Учтем, что 6С = 0 в пределе пластической деформации, и используем линейную аппроксимацию зависимости 61с(е) :
6(e) = 6 1с - (^-) Е. Етах
В вершине трещины КРТ определяется известной зависимостью линейной механики разрушения:
б^)
Коэффициент Л [12] находится по формуле:
^ (1-2ц)2Е / q^ w+1 1,24пот RmceD/
.
Здесь Е — модуль упругости материала; Rmce — напряжение микроскола деформированного материала; D — коэффициент, учитывающий повышение первой главной компоненты напряжения для случая сложнонапряженного состояния; q — коэффициент, показывающий отношение второй главной компоненты
напряжений к первой; m — коэффициент упрочнения.
Для указанных характеристик и коэффициентов существуют вполне определенные расчетные зависимости по основным механическим характеристикам материала. Критический коэффициент
Машиностроение и машиноведение
интенсивности напряжений в (12) рассчитывается по формуле:
—+1
К1с = (-^—У" о т • 6,18ndz, (14)
\ qoT )
где dz — средний диаметр зерна исходного материала мягкой прослойки. Подставим последнее выражение и (13) в (12). Сделаем необходимые сокращения. Учтем, что в (12) и (11) можно пренебречь малой составляющей упругих деформаций. В итоге получим:
61С(£) = 5(1-2^(1-^).
Деформация е вычисляется по зависимости (10). Найдем зависимость К1с(е) . Из (12) имеем К1с(е) =
^Е от61с(е')/Х . Подставим известные выражения и получим:
^л+1
-
- 6Д8п^Т(1-Э
^\ q^T ' v 100'
или
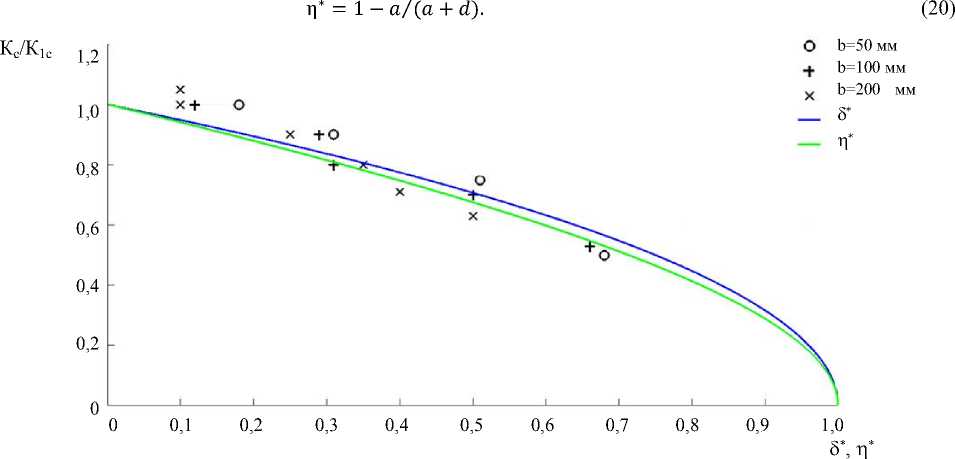
0,618^2 к1с(6)= 4-1-------(—у Л1-105ln(1 + 6)l J о™ (1 — 2ц)24 После упрощения можно получить простую зависимость критического коэффициента интенсивности напряжений К1с от текущей величины 6 вытягивания мягкой прослойки: К1с(6) = Кс = К1с^1—^^1п(1 + 6), где 6 — удлинение (вытягивание) материала мягкой прослойки, доли. В формуле (18) К1с(6) — предел трещиностойкости Кс. Его относительное значение К1с(6)/К1с показывает, как снижение вязкости разрушения материала зависит от удлинения (вытягивания) элементарной области мягкой прослойки. Для простоты расчетов можно использовать усредненное удлинение мягкой прослойки под полезной нагрузкой. Отметим, что локальность пластического удлинения в сварном соединении мягкой прослойки на ДА относительно А может существенно влиять на ее усталостную прочность. Для упрочненного основного материала это влияние, наоборот, будет незначительным (рис. 1). При 6 = 65 отношение Кс/К1с должно давать ноль, поэтому приравняем (18) к нулю и запишем относительно 6 расчетную формулу: 65 = ехр(100/о,) — 1. (19) Здесь о, подставляется в МПа. Анализ результатов и проверка адекватности полученных зависимостей. Можно признать удовлетворительными результаты проверки согласования расчетных характеристик по полученным аналитическим зависимостям со справочными данными конструкционных сталей феррито-перлитного класса в состоянии поставки. Речь идет о тонколистовом прокате из стали Ст10, Ст50, 22К, Ст3сп, 37ХН3А, 30ХГСА и др. (таблица 1). Расчетные и справочные характеристики сталей Таблица 1 Сталь ов, МПа от, МПа m dz, мкм Фк К1с, МПаТм 65, % 65,% Ст10 320 190 0,17 66 0,73 103,6 36,6 > 31 15Г 410 245 0,148 94 0,55 104 26,4 26 Ст3сп 450 270 0,16 37 0,71 101 24,8 25 22К 540 310 0,16 30 0,69 97 20,3 22 „.26 Ст50 680 350 0,16 25 0,62 78 15,8 17 10ХСНД 540 390 0,132** 27 0,71 — 20,3 19 37ХН3А 1014 743 0,12 7 0,6 73,8 10,3 10 30ХГСА 1750 1360 0,09 3 0,44 53,2*" 6 7 30ХГСА 1470 1080 0,12 4 0,6 58,5*** 7 7 *Расчет по (19); **расчет по m = {0,75 • Zg[oB(1 + 1.4фк)/о0.2]}/Zg [105 • Zn (~“) /(200 + 0,5о0,2)] [15]; ***расчет по (14). Выполненный ранее анализ [12] подтверждает, что коэффициент Л, рассчитанный по (13) при КРТ в вершине 0,618dz, согласуется с экспериментальными данными для сталей 22К и Ст10. В первом случае X равен 0,22, во втором — 0,23. Рассмотрим предварительную деформацию тонких листов при плоском напряженном состоянии с условием, что зерно получит относительное удлинение ez в продольном направлении. В этом случае средний его диаметр в том же направлении будет больше в (1 + ez) раз, а в поперечном уменьшится в (^1 + ez). То есть, если в продольном направлении средний диаметр возрастет в 2,618 раза, то в поперечном он уменьшится в 1,618 раза. Здесь поперечное направление совпадает с направлением движения трещины. Легко видеть линейность зависимости, по которой определяется увеличение среднего диаметра зерна. Из этого следует, что при равномерном одноосном пластическом деформировании критическое раскрытие в вершине трещины тоже должно снижаться линейно, в зависимости от относительного удлинения ez. При прокатке стальных листов такой выраженной линейной зависимости не обнаруживается. Очевидно, это связано с поперечными деформациями, для которых характерна приплюснутость зерен. Диаграммы изменения К1С как функции от 6 для сталей (таблица 1) приведены на рис. 2. Рис. 2. Изменение трещиностойкости в зависимости от предварительного удлинения сталей Критический коэффициент интенсивности вычислен по (14) с использованием данных таблицы 1. Это позволяет определить уровень К1С при пластической деформации вытяжкой и сопоставить его со значениями других сталей. Так, сравнение стали 30ХГСА, обработанной на величину предела текучести от = 1360 МПа, и стали 10 показывает, что при использовании низкопрочной стали 10 уровень К1С можно снизить только при больших деформациях удлинения (около 25 %). На практике в конструкциях так бывает достаточно редко. Однако при целенаправленной вытяжке или холодной прокатке возможно существенное снижение К1С, и это следует учитывать. Если стали ранжировать по предельной пластичности и сопоставить для них максимальные значения К1С, то окажется, что пластичность убывает от одной марки стали к другой гораздо быстрее, чем меняется критический коэффициент интенсивности напряжений. Так, К1С для сталей 30ХГСА и 10 в исходном состоянии поставки отличается в ~2 раза, а относительное удлинение 6 — в ~5 раз. Появление пластичности в вершинах различных концентраторов напряжений неизбежно, поэтому для обеспечения необходимой надежности элементов из стали 30ХГСА целесообразно контролировать пластические деформации в конструкции в ∼5 раз точнее. Кроме того, необходимо учитывать, что снижение вязкости в ∼2 раза приведет к снижению критической длины трещины в ∼4 раза. Причина — низкая вязкость и пластичность стали 30ХГСА, для эксплуатации которой придется в ∼5 раз увеличить коэффициент запаса прочности. Последнее не означает, что высокопрочные стали как конструкционный материал хуже сталей средней прочности. Проблема заключается в выборе оптимального сочетания вязкости, пластичности и прочности. Полученные в настоящем анализе расчетные зависимости дают возможность оценить данные характеристики расчетным путем. Это важно для рационального выбора материала на этапе конструирования, определения оптимальных режимов сварки и термообработки. Сопоставим результаты расчетов по (18) с известной зависимостью (7)8 (рис. 3). Первая функция зависит от оставшейся пластичности стали, а вторая — от относительной длины трещины в концепции Машиностроение и машиноведение структурного элемента. Чтобы удобно представить результаты для их сравнения, введем безразмерный параметр: Рис. 3. Зависимости относительного предела трещиностойкости от безразмерного параметра дисковидной трещины п* и от безразмерного параметра предварительного равномерного удлинения материала б*. Линии — аналитические зависимости (7), (18). Маркеры — экспериментальные данные для компактного образца9 [11, 16] с размерами b После подстановки (20) в (7) получаем инвариантное выражение для среднего значения. Если известно П*, то можно найти отношение а/(а + d) по (20). Результаты сравнения показывают, что функции практически совпадают. В относительных координатах для них характерна инвариантность с хорошим приближением. Обе функции хорошо аппроксимируют экспериментальные данные предела трещиностойкости, полученного на образцах с характерными размерами b [13]. Рассмотрим условия плоской деформации при известной критической длине трещины Lc. Для ферритоперлитных сталей с от< 400 МПа ее приближенно можно оценить как Lc = 2K2Jn/oTt и легко найти критическое напряжение внешней нагрузки ос = Kc/^nLc: ос = от |1 —^|п(1 + б). (21) 2 2 0 0 Уравнение отражает закон уменьшения критических напряжений ос ниже значения предела выносливости материала с длиной трещины Lc в зависимости от величины предварительного удлинения материала. В этой же постановке снижение критической длины трещины в предварительно деформированном материале мягкой прослойки можно оценить по зависимости: L=-(—)2(1-дв;|п(1 +б)), (22) п о 100 где L — половина длины для сквозной тещины; о — критическое напряжение для катастрофического распространения трещины длиной L. При о = о-1 из (22) следует, что длина L катастрофического распространения трещины прямо пропорциональна значению (1 — ^Мп(1 + б)) и константе материала мягкой прослойки Lc. Полученные зависимости в системной совокупности представляют предлагаемую математическую модель оценки трещиностойкости сварных соединений с мягкими прослойками. Обсуждение и заключение. При сварке термоупрочненных сталей для корпусных и других листовых конструкций образуются мягкие прослойки, металл которых пластически деформируется в первых циклах нагружения. Методами численного анализа с применением CAE-средств10 можно определить деформации или увеличение ширины мягкой прослойки сварного соединения под действием рабочих нагрузок. Надежность работы соединения с мягкой прослойкой зависит от степени пластической деформации, ее упрочнения, жесткости напряженного состояния с учетом приграничных зон твердых прослоек, а при появлении трещины — от ее критической длины L. При вытягивании мягкой прослойки L снижается прямо пропорционально константе материала мягкой прослойки Lc и выражению, зависящему от степени вытягивания 6, т. е. от относительного предварительного удлинения.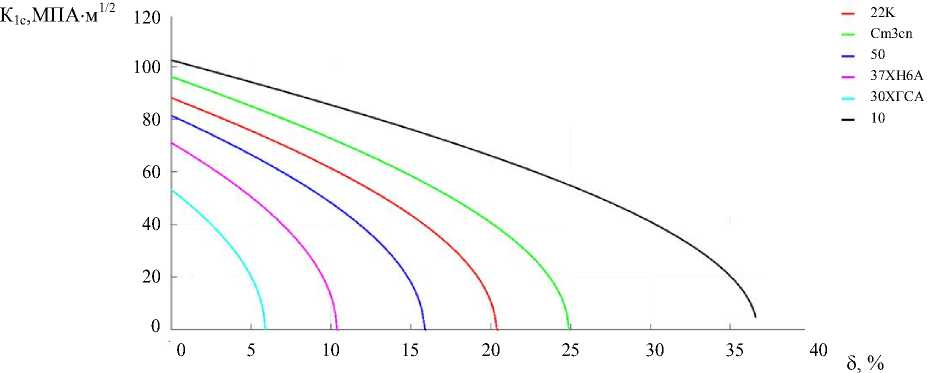
Список литературы Оценка трещиностойкости сварных соединений с мягкими прослойками
- Повреждения и расчетный анализ прочности корабельных конструкций / В. В. Новиков, Г. П. Турмов, О. Э Суров [и др.]. — Владивосток : ДВФУ, 2020. — 266 с.
- Махутов, Н. А. Деформационные критерии разрушения и расчет элементов конструкций на прочность / Н. А. Махутов. — Москва : Машиностроение, 1981. — 272 с.
- Компьютерное моделирование контактного упрочнения алюминиевой прослойки магниево -алюминиевых цилиндрических сосудов / Л. М. Гуревич, Ю. П. Трыков, И. А. Пономарева, В. Н. Арисова // Вестник Сибирского государственного индустриального университета. — 2015. — № 4 (14). — С. 12-16.
- Айметов, С. Ф. Прочность стыковых сварных соединений, ослабленных мягкой прослойкой, при действии изгибающей нагрузки / С. Ф. Айметов, Ф. Г. Айметов // Вестник Южно-Уральского государственного университета. — 2015. — Т. 15, № 1. — С. 107-112. — (Металлургия).
- Влияние неоднородности механических совйств различных зон сварного стыкового соединения на работу соединения в упругопластической стадии деформации / В. И. Берг, М. Н. Чекардовский, С. В. Якубовская, В. С. Торопов // Современные проблемы науки и образования : [сайт]. — 2015. — № 2/3. — 28 с. — иКЬ: http://www.science-education.ru/ru/article/view?id=23518 (дата обращения: 11.02.2021).
- Кулиев, В. Д. Разрушение многослойных материалов с усталостной трещиной / В. Д. Кулиев, я Ю. В. Зайцев, П. С. Султыгова // Известия Казанского государственного архитектурно-строительного ^ университета. — 2014. — № 3 (29). — С. 162-166. В
- Оценка надежности судовых конструкций с микротрещинами и остаточными сварочными напряжениями / К. А. Молоков, В. В. Новиков, Г. П. Турмов, Н. П.Васильченко // Морские интеллектуальные технологии. — 2018. — Т. 1, № 3 (41). — С. 45-54. §
- Молоков, К. А. Оценка поврежденности феррито-перлитных сталей при перегрузках / К. А. Молоков, о А. В. Славгородская // Морские интеллектуальные технологии. — 2013. — № 2. — С. 56-58.
- Бирдегулов, Л. Р. Исследование трещиностойкости металлов / Л. Р. Бирдегулов, А. М.Щипачев // scientia. — 2016. — № 2. — С. 28-32. К
- Аснис, А. Е. Динамическая прочность сварных соединений из малоуглеродистой и й низколегированной сталей / А. Е. Аснис. — Москва ; Киев : Машгиз, 1962. — 171 с.
- Матвиенко, Ю. Г. Двухпараметрическая механика разрушения / Ю. Г. Матвиенко. — Москва : Физматлит, 2021. — 208 с.
- Матохин, Г. В. Оценка ресурса сварных конструкций из феррито-перлитных сталей / Г. В. Матохин. — Владивосток : ДВГТУ, 2001. — 202 с.
- Прочность, ресурс, живучесть и безопасность машин / Отв. ред. Н. А. Махутов. — Москва : Либроком, 2008. — 576 с.
- Зоны локализации пластической деформации в предварительно деформированных тонколистовых пластичных материалах / В. Ю. Гольцев, А. В. Зеленский, О. Г. Кудрявцев, Ю. Г. Матвиенко // Исследование прочности материалов и конструкций атомной техники. — Москва : Энергоатомиздат, 1984. — С. 68-73.
- Научные основы повышения малоцикловой прочности / Н. А. Махутов, К. В. Фролов, М. М. Гаденин [и др.] ; под ред. Н. А. Махутова. — Москва : Наука, 2006. — 623 с.
- Сосновский, Л. А. Трещиностойкость / Л. А. Сосновский, А. В. Богданович. — Гомель : БелГУТ, 2011. — 366 с.
- Математические модели оценки эксплуатационного ресурса и работоспособности судовых сварных конструкций / К. А. Молоков, В. В. Новиков, Г. П. Турмов, А. С. Владимирович. — Владивосток : Дальневосточный федеральный университет, 2021. — 240 с.


