Оценка трудоемкости моделирования динамики сложных систем

Моделирование динамики сложных организационно-технических систем занимает важнейшее место в современных исследованиях, направленных на обоснование их рациональных структур и параметров. К подобным системам могут быть отнесены как системы специального назначения (управления вооружением и

военной техникой, радиоэлектронной борьбы и им подобные), так и общегражданской направленности (скорой помощи, пожарной охраны, управления и обеспечения полетов гражданской авиации, системы общегородских коммуникаций), а также системы, включающие в себя ресурсы отдельно взятого предприятия промышленности, транспортной организации и т. п.

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License

С возрастанием сложности современных систем возрастает количество входящих в их состав структурных элементов. Соответственно, резко возрастает трудоемкость моделирования.

Например, городская станция скорой помощи в общем случае имеет структуру и порядок функционирования, приведенные на рисунке 1.

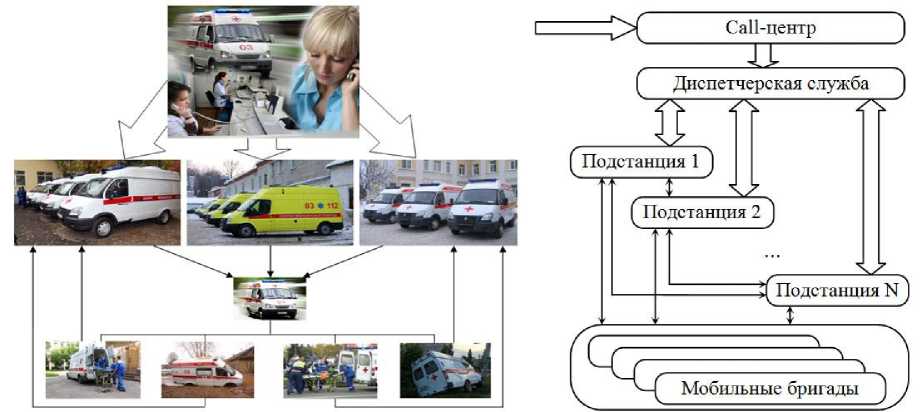
Рисунок 1. Структура и схема функционирования городской станции скорой помощи

Figure 1. The structure and scheme of functioning of the city ambulance station

Каждая из подстанций получает поток входящих заявок от Call-центра и диспетчерской службы городской станции. Как Call-центр, так и диспетчерская служба представляют собой системы массового обслуживания (СМО). В свою очередь, каждая подстанция комплектуется бригадами скорой помощи, имеющими определенное оборудование и предназначенными для решения определенного круга задач. Количество бригад отдельной подстанции в первом приближении может быть интерпретировано как количество каналов, обслуживающих входящий поток заявок. С учетом специфики деятельности экипажей это представление также распадается на ряд частных моделей СМО, между которыми делится поток входящих заявок. Возможно также перенаправление заявок от одной СМО к другой в случае острой необходимости. Следовательно, модель подобной организационно-технической системы представляет собой иерархически организованную структуру частных моделей СМО, имеющих дополнительные взаимные связи в пределах каждого уровня (рисунок 2).

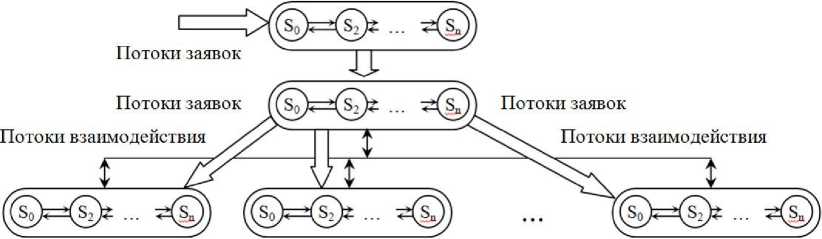
Рисунок 2. Иерархически организованная структура частных моделей СМО городской станции скорой помощи

Figure 2. Hierarchically organized structure of private models of the CMO of the city ambulance station

Модели СМО верхнего уровня можно считать имеющими характеристики, приближающиеся к идеальным, так как вероятность отказа этой подсистемы стремится к нулю. Время задержки заявки, обусловленное естественными причинами, в большинстве случаев также стремится к нулю, и лишь иногда может составлять заметный временной интервал.

В отличие от модели диспетчерской службы, модели СМО нижнего уровня характеризуются значительными величинами времени обслуживания заявки. Выезд по адресу, задержки в пути следования, время на выполнение лечебных мероприятий или доставку пациента в стационар, возвращение к месту расположения подстанции – все эти факторы дают в сумме случайную величину, распределенную по отличному от экспоненциального закону, поскольку мода распределения плотности вероятности суммы случайных величин не может иметь малые значения. Тогда оценки, получаемые на марковских моделях СМО с экспоненциальными распределениями, могут оказаться весьма далеки от реальных характеристик системы.

Дополнительные сложности моделирования возникают при попытке учета особенностей смены состояний каждым из структурных элементов СМО. Пример графа состояний отдельной бригады скорой помощи, моделируемого отдельным каналом СМО, приведен на рисунке 3.

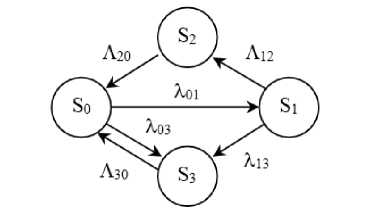
Рисунок 3. Граф состояний отдельной бригады скорой помощи

Figure 3. State graph of a separate ambulance brigade

На графе S 0 – состояние работоспособности и ожидания заявки (state of health and waiting for the application), S 1 – состояние получившей заявку бригады (the status of the brigade that received the application), S 2 – состояние бригады, которая начала обслуживание пациента (М), S 3 – a state defined as a failure of the QS channel as a result of equipment failure, vehicle failure or illness of one of the doctors in state S 0 , or any incident en route in state S 1 . Переходы S 0 – S 1 , S 0 – S 3 , S 1 – S 3 , определяемые потоками внешних случайных событий, можно считать марковскими с экспоненциальным распределением вероятностей. В то же время переходы S 1 – S 2 , S 2 – S 0 , S 3 – S 0 , определяемые потоками выполняемых в самой системе мероприятий, считать марковскими никак нельзя, поскольку они почти занимают некоторый отрезок времени и, следовательно, подчиняются законам распределения вероятностей, отличным от экспоненциального. Кроме того, количество каналов каждой СМО становится случайной величиной, что затрудняет возможность применения результатов классической теории для получения аналитических оценок.

В общем случае количество состояний организационно-технической системы определяется как N = nm, где n – количество состояний отдельного структурного элемента. Например, если имеется всего лишь m = 7 различных элементов (СМО), для каждого из которых известны n = 2 состояния, то общая модель должна включать в себя N = 27 = 128 состояний.

Исчерпывающий анализ немарковской динамики систем, подобных рассмотренной, основан на решении систем дифференциальных уравнений, либо реализуется методами имитационного моделирования. С указанными выше исходными данными требуются затраты колоссальных вычислительных ресурсов для решения задачи интегрирования систем дифференциальных уравнений численными методами. Имитационное моделирование также требует десятков и сотен тысяч реализаций для получения достоверных результатов. Поэтому непреходящую актуальность имеют задачи получения оценок вероятностей иными методами, по крайней мере, для стационарного режима функционирования.

Материалы и методы

• 1.1    Предмет и цель исследования

Исследованию моделей динамики систем с дискретными состояниями и непрерывным временем посвящено большое количество классических и современных трудов. Модели марковских непрерывных цепей наиболее полно рассмотрены в [1–3], включая модели СМО различного вида. Полумарковские модели, для произвольных в общем случае законов распределения вероятностей в стохастических потоках событий, основанные на методе Кендалла и методе вложенных марковских цепей, освещены в [4, 5]. Различные оценки для систем массового обслуживания с учетом современных реалий формирования потоков данных получены в циклах статей А. Зейфмана и других авторов, представленных в трудах ежегодной конференции Европейского Совета по моделированию [6–17]. Подходы на основе имитационного моделирования рассмотрены в [18, 19]. Отдельного внимания заслуживают методы представления произвольных законов распределения в виде смеси экспоненциальных законов и последующего применения марковских моделей [20, 21].

Авторы данной статьи в своих исследованиях [22–25] опираются на факт изоморфизма марковских и немарковских моделей, обусловленный идентичными множествами состояний моделей и идентичными множествами переходов между состояниями. Исключая из рассмотрения переходный процесс модели, для стационарного режима может быть найдено марковское представление, доставляющие те же вероятности состояний, что и модель с неэкспоненциальными распределениями вероятностей.

Предметом исследования является обобщенная модель динамики сложной системы с дискретными состояниями и непрерывным временем, граф которой приведен на рисунке 4.

Предполагается, что в направлении каждой дуги на систему воздействует стохастический поток событий, причем первое же событие потока переводит систему в новое состояние. Функции распределения вероятностей F ij (t) для временных интервалов в потоках известны. Моменты распределений F ij (t) :

го my = j tdFy (t);

го

D = ^ ² =K t - m y ⁽ t ) ) dF j ⁽ t )

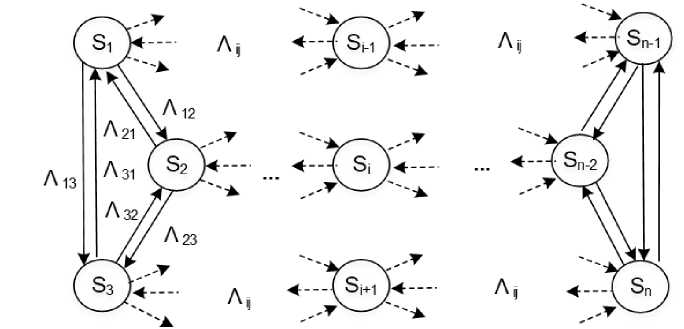
Рисунок 4. Граф обобщенной модели динамики системы

Figure 4. Graph of a generalized model of system dynamics

Основной задачей моделирования является определение значений вероятностей P i возможных состояний системы.

Марковские модели адекватны только для очень небольшого класса реальных процессов с экспоненциальным распределением вероятностей. Методы же имитационного моделирования в большинстве случаев приводит к существенным вычислительным затратам, как и полумарковские модели. Вместе с тем сочетание этих подходов может позволить существенно снизить трудоемкость решения задачи оценивания вероятностей состояний системы в стационарном режиме.

Цель исследования – обоснование методического подхода, позволяющего с учетом изоморфизма моделей различных классов разработать расчетные алгоритмы, соизмеримые по трудозатратам с марковскими моделями, позволяющие получить оценки вероятностей состояний сложных систем для произвольного вида законов распределения вероятностей в стохастический потоках событий.

• 1.2    Оценка известных методов моделирования

В качестве основного аналитического подхода, применяемого для анализа динамики систем с последействием, применяются полу-марковские модели .

Интенсивность рекуррентного потока

Л у = 1/ m y .                 ⁽²⁾

Если функция распределения вероятностей подчиняется экспоненциальному закону

F y ( t) = 1 — e - ^{x t} ,                  (3)

то поток событий является простейшим (пуассоновским), для которого:

^ст у = m y ;   D y = m y^тх    ^Лу = A y = 1/m y . (4)

Наиболее доступно и вместе с тем полно полумарковский подход освещен в [4, 5]. Полу-марковские модели основаны на методе вложенных цепей Маркова, предложенном Д. Кендаллом в 1953 году. Полумарковские модели, будучи точным математическим аппаратом, очень сложны. Построение подобной модели для более чем 5–6 состояний может служить предметом достаточно длительного научного исследования.

Рассмотрим более подробно стационарный режим полумарковской модели. Отдельно взятое состояние процесса приведено на рисунке 5.

Fi1

------^ Si J ------* Fi2

Fi3

Рисунок 5. Отдельно взятое состояние полумарковского процесса

• Figure 5. Separately taken state of the semi-Markov process

Переходные вероятности вложенной марковской цепи p ij (t) могут быть определены как вероятности, что процесс совершил переход в направлении S i → S j , при условии того, что в это же время он не совершил переход в любом другом направлении S i → S k .

Тогда:

¥

Р ч = Р ч ^(¥) = J П ( 1 - F ik ^{( t} ) )dF y ^{( t} )

⁰ k ¹ y                               (5)

2 j = 1.

ч * i

Рассуждая далее, можно говорить, что если имеют место переходные вероятности вложенной марковской цепи, то должны быть и некоторые вероятности состояний этой абстрактной цепи. Тогда для стационарных значений вероятностей имеем:

nj =2n■ Py, jeE i E E

1                                    ,             (6)

2 n = ¹

l j e E

Выражения (15) позволяют оценить асимптотическое или стационарное поведение процесса при t → ∞ , исключив ряд сложных интегральных уравнений.

Перейдем к анализу полумарковского процесса с точки зрения временной составляющей. Условная функция распределения пребывания процесса в состоянии S i до перехода в состояние S j при условии единственности перехода:

F y (t ) = P ( t_y < t\^ (0) = i , £ ( t ) = j ) ,       (7)

при этом P ij ( t ) = P ij F ij ( t ) .

Тогда безусловная функция распределения продолжительности пребывания процесса в состоянии S i до перехода в любое другое состояние S j имеет вид:

F ⁽ t ) = ^{P (} t y <  t ) = 2 P j F j ⁽ t ) = 2 Р у ⁽ t )

J e E             J e E i * j                i * j dFt(t)          dFj (t)

f. ⁽ t ) =      = 2 Py —F~ = 2 Pjfy ⁽ t ).

dt   JeE    dt    jeE l * J                     I * J

Эта функция может быть также определена через функции распределения времени между событиями в стохастических потоках, исходящих из данного состояния:

Fi (t) = 1-П (1 - Qy (t)).(9)

Математическое ожидание времени пребывания процесса в состоянии S i :

TOTO т- = jtfi(t)dt = 2PyJtfy(t)dt = 2PyTy.(10)

0             j e E    0

i * ji

И, наконец, определяются предельные вероятности полумарковского процесса:

Ф, = -i^T^-.

in

2 П • Ti i=1

Очевидно, что с учетом сложности некоторых функций распределения вероятностей решение (5) и (10) может являться нетривиальной задачей. Как правило, эти задачи решаются численными методами интегрирования.

Модели непрерывных марковских цепей.

Уравнения Колмогорова-Чепмена.

В основе этого класса моделей лежит до- пущение о том, что распределение временных интервалов для всех потоков событий подчиняется экспоненциальному закону. Уравнения Колмогорова-Чепмена для стационарного режима имеют следующий вид:

dP, (t )            ”         ”

^y =- ^pj ( t ) 2 ^x Jk ⁺2 ^p- (t) ^ iy ^,   j = ^1,2Д

n

2 p - ( t ) = 1

i = 1

n ;

Алгоритмы решения подобных систем широко известны (Гаусса, обращения главной матрицы, итерационные методы и т. д.). Решение СЛАУ стационарного режима марковской модели методом Гаусса без выбора главного элемента при N сост > 10 требует

F_a ( n ) « - N_co J a            сост

арифметических действий. В то же время для модели с большим количеством состояний может быть применен метод простой итерации, с оценкой

F a ( n ) » I ■ 2 N cocm ² ,              (14)

где I – количество итераций для достижения требуемой точности.

Итерационные методы можно делать даже более эффективными, изменяя некоторые параметры приближений. Таким образом, математический аппарат марковских цепей с непрерывным временем является достаточно простым, в особенности для стационарного режима процесса. В то же время область его применения ограничена, так как большинство процессов могут иметь разнообразные функции распределения случайных величин.

Имитационные модели (метод Монте-Карло)

Достоверность моделирования, точность и количество реализаций имитационной модели связаны соотношениями, опирающимися на неравенство Чебышева:

-

^P (I t cp ^{- M}V\\ ^ ^S ) ^ ^ ^ ,       ^ tep ² = ^ N , ⁽¹⁵⁾

где tср – выборочное среднее моделируемого параметра (sample mean of the modeled parameter); Mt1 - математическое ожидание модуля параметра (mathematical expectation of the modulus of the parameter); ε – точность оценивания параметра (parameter estimation accuracy);

G t - среднеквадратическое отклонение параметра (parameter standard deviation); a - достоверность полученной оценки (reliability of the obtained assessment).

Тогда требуемое количество реализаций модели:

N реализ

G 2

>    '. ■-.

s ²   ( 1 - a )

Полагая s ~ 0,01 O t , а достоверность результатов на уровне a = 0,99, получим:

N«mиз = 0,012 ■ 7—1—7 = 106.

реализ           (|_q 99)

Рассмотрим количественно-зависимый аспект трудоемкости имитационного моделирования. Граф может варьироваться от полносвязного графа до варианта с единственным исходящим из данного состояния потоком. В среднем из каждого состояния исходит N сост /2 потоков событий. Тогда для отдельно взятого состояния:

N

• ^- = -от -< 10 6           ⁽¹⁸⁾

Поочередное моделирование всех состояний, при равной их вероятности, потребует

• -ре» = = "сот" ■Ю⁶ .           (19)

реализ

Расчет каждой случайной величины в реализации осуществляется на основе степенных рядов и относится к параметрически-зависимым по трудоемкости алгоритмам.

В простейшем случае экспоненциально распределенная величина ф генерируется методом обращения функции распределения. Для получения в дальнейшем оценки Ω(n) достаточно положить, что данная реализация требует не менее 10 вычислительных операций.

К трудоемким случаям можно отнести, например, генерацию случайной величины в, подчиненной гамма-распределению Г(θ, k). Она выполняется следующим образом в = 6

(      [ к ]

§ Z ^ln Y i

_V         i = 1

где [ k ] – целая часть параметра k (integer part of the parameter k ); ξ – гамма-распределенная случайная величина с нецелочисленным параметром { k } (gamma-distributed random variable with integer parameter { k }), {k} = k – [ k ]; θ – параметр гамма-распределения (gamma distribution parameter).

Однократный проход данного алгоритма, с учетом выполнения нелинейных операций при помощи степенных рядов, включает в себя до 103 простых операций.

С учетом (22) окончательно приходим к следующим оценкам

F a ( n ) = О ( 10 9 N cocm ³ ) ;

F a ( П ) =fi ( 5 - 10 ⁶ - сост ² ) .

Неравномерность по вероятности динамики процесса дополнительно увеличивает количество реализаций. Выражение (18) должно применяться на том подмножестве состояний, где вероятность минимальна. Тогда на других подмножествах состояний будем иметь избыточное количество реализаций.

Полагая P max = kP min и равномерное приращение значений вероятностей на всем множестве состояний модели, получим

N реализ

N реализ

² сост

³ сост

, 10 6 + У от' , 10 6 ■ к_ 1 ■ ( - сост

—

■ 10 6 1 к — 1 + 3—k-N

V           сост

.

В предположении k « 5 и достаточно большого количества состояний модели получаем:

Следует иметь в виду, что нижняя оценка Ω(n) здесь получена в предположении, что все величины распределены экспоненциально, то есть для марковской модели.

Итак, имитационное моделирование отличается:

• •    высокими требованиями к реализации логики алгоритма модели;

• •    колоссальными потребностями в вычислительных ресурсах при проведении эксперимента.

Для сравнения трудоемкости различных подходов обратимся к (13) и нижней оценке из (24). Имитационное моделирование может оказаться предпочтительнее аналитического при

- сост > 2 ■ 5 , 10 ⁶ = 7,5-10 ⁶ , (25)

реализ      сост

.

Таким образом, из (19) и (21) следует:

реализ min           сост реализ max        сост

;

.

что вряд ли может встретиться реальных задачах.

В то же время метод простой итерации при I < N сост имеет заведомо меньшую трудоемкость (14), чем оценка (24) для имитационного моделирования.

Таким образом, краткий обзор известных методов анализа динамики сложных технических систем показывает, что марковские модели отличаются сравнительной простотой и доступностью требуемых вычислительных ресурсов. Однако в целом ряде задач эти модели нельзя считать адекватными реальным процессам. Полу-марковские и имитационные модели позволяют исследовать все множество реальных процессов, но очень сложны и трудоемки. Это существенно ограничивает их практическое применение.

Вместе с тем, всем указанным моделям присуще свойство взаимного изоморфизма.

Представляется перспективным применение декомпозиции модели, имитационного моделирования для отдельных ее состояний, установление на этой основе изоморфных марковских представлений, композиция вновь сформированных состояний модели и финальный расчет вероятностей путем решения систем линейных уравнений.

Марковские модели немарковских процессов

Метод базируется на изоморфизме марковских и немарковских моделей (рисунок 6).

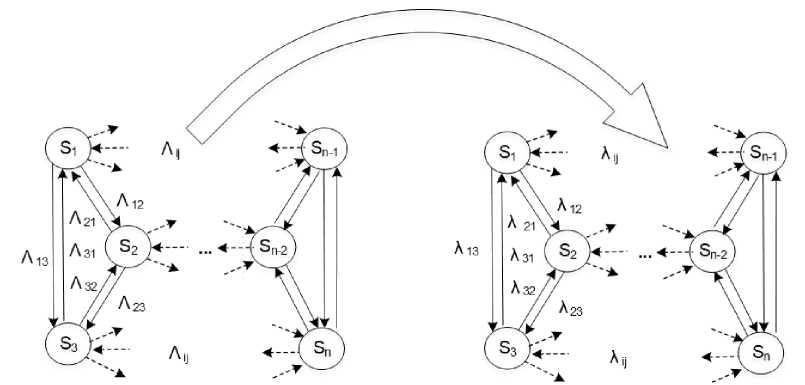
Рисунок 6. Наличие и единственность изоморфной марковской модели

• Figure 6. Presence and uniqueness of an isomorphic Markov model

Справедливо следующее утверждение.

Для любой модели случайных блужданий системы на множестве дискретных состояний с непрерывным временем и неэкспоненциальными в общем случае законами распределения временных интервалов в потоках событий F ij (t) = G , переводящих систему из одного состояния в другое, всегда найдется изоморфная марковская модель, притом единственная, включающая те же состояния и переходы и доставляющая те же оценки стационарных вероятностей состояний модели.

Для обоснования этого положения авторами доказан ряд теорем. Предполагалось, что стационарные значения вероятностей состояний P i (t) = P i = const немарковской модели {( F ij (t) = G, m ij , σ ij )} уже получены каким-либо из общепринятых подходов. Интенсивности переходов изоморфной марковской модели { λ ij }, напротив, полагались неизвестными. В теоремах на основе анализа главной и вспомогательной матриц системы уравнений доказано, во-первых, наличие решения для любых значений вероятностей состояний, а во-вторых, единственность такого решения.

Алгоритм применения марковских моделей для немарковских процессов имеет вид.

• 1)    Выбирается отдельное состояние модели S i ., вместе с исходящими из него потоками событий (рисунок 7).

• 2)    Для выбранного состояния S i строится замыкание исходящих потоков так, как это показано на рисунке 8.

Вид и параметры каждого исходящего из S i потока Λ ij сохраняются. Из каждого псевдосостояния Z j в рассматриваемое состояние S i направляется простейший поток с интенсивностью λ ji .

Важное замечание. В зависимости от вида и количества исходящих потоков возможны частные случаи, которые существенно снижают вычислительные затраты на моделирование. Они рассмотрены отдельно, после общего алгоритма.

• 3)    Выполняется имитационное моделирование на построенной частной модели, с оценкой стационарных значений вероятности P' i состояния S i и вероятностей P' j состояний Z j .

• 4)    Вычисляются параметры простейших потоков, заменяющих рекуррентные потоки исходной модели, по формулам

xjiP'j хи = ——J-; mi,■ = 1 \i;

ij                                 ij               ij

P j

^П Р ^И ^ ji = ¹    ^ ij="^ .

• 5)    Пункты 1–4 выполняются для всех состояний модели.

• 6)    Состояния S i с вновь определенными простейшими потоками λ ij объединяются в общую модель, изоморфно исходной модели.

• 7)    На полученной марковской модели рассчитываются стационарные значения вероятностей состояний P i путем решения системы линейных уравнений Колмогорова-Чепмена. Полученные стационарные значения вероятностей P i будут равны стационарным значениям вероятностей состояний исходной модели с рекуррентными потоками.

Конец алгоритма.

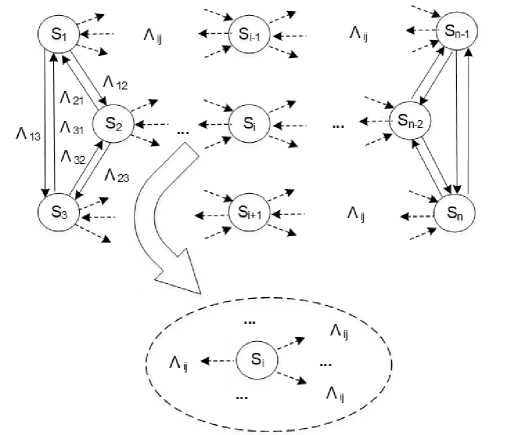
Рисунок 7. Выбор отдельного состояния Si с исходящими потоками событий

Figure 7. Selection of a single state Si with outgoing event streams

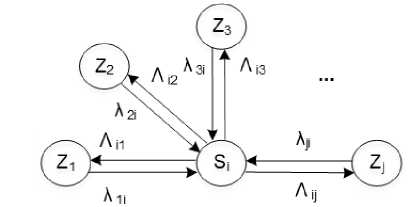
Рисунок 8. Замыкание исходящих потоков состояния Si

Figure 8. Closure of the outgoing streams of the state Si Частные случаи при анализе отдельного состояния модели (к шагу 2 алгоритма):

• А.    Случай, когда из состояния выходит единственный поток, являющийся рекуррентным (рисунок 9):

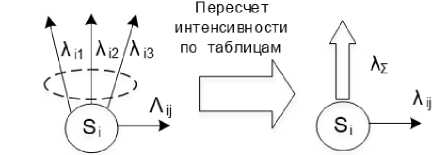
Рисунок 9. Изоморфная модель для единственного рекуррентного потока

Figure 9. Isomorphic model for a single recurrent stream

Доказано, что для искомой изоморфной марковской модели интенсивность простейшего потока равна интенсивности рекуррентного потока.

Б. Случай, когда из некоторого состояния выходит один рекуррентный поток, а прочие потоки – простейшие. Тогда интенсивности простейших потоков суммируются (рисунок 10).

После этого можно воспользоваться таблицами коэффициентов пересчета интенсивности рекуррентного потока. Необходимость имитационного моделирования отпадает.

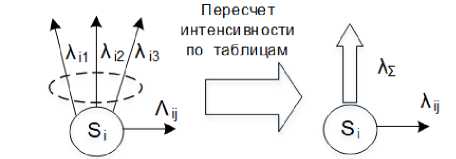
Рисунок 10. Получение изоморфной модели для одного рекуррентного потока

Figure 10. Obtaining an isomorphic model for one recurrent stream

• В.    Случай, когда из состояния выходят несколько рекуррентных потоков и два или более простейших потоков (рисунок 11).

  

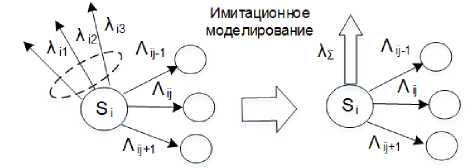
  Рисунок 11. Снижение размерности моделирования путем объединения нескольких простейших потоков

  Figure 11. Simulation dimension reduction by combining several simple streams

  
  

  При декомпозиции затраты на имитационное моделирование для каждого из состояний будут иметь одинаковый порядок, определяемый только интенсивностями потоков, исходящих именно из этого состояния. Выражение (22) оценивает приращение реализаций за счет неравномерности распределения вероятностей по состояниям модели. Тогда

  
  

  N

  реализ max

  
  

  сост

  
  
  
  

  N

  реализ min

  
  

  5 ⋅ 10 ⁵ N сост

  
  

  - = 2N

  2        сост

  
  
  
  

Тогда количество замыканий для потоков существенно снижается, так как простейшие потоки объединяются. Имитационное моделирование существенно упрощается.

Результаты

Снижение вычислительных затрат за счет декомпозиции модели.

Здесь выигрыш достигается путем выполнения имитационного моделирования отдельно для каждого состояния.

В исходной модели для достижения требуемого уровня достоверности и точности результатов определяющую роль играет количество сгенерированных переходов на подмножестве состояний { S" } с минимальным значением вероятности состояния. В свою очередь, на этом подмножестве следует выбрать переходы с минимальной интенсивностью потока событий (рисунок 12).

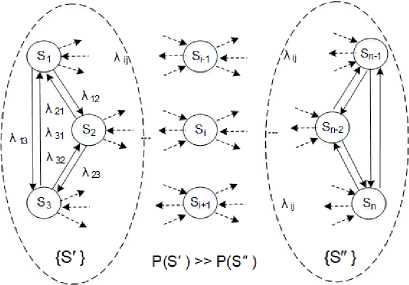
Мреализ(5 ) ^Иреализ^о ) Np_em«₃(S')= F (М_р6ал„з(3" )) Npeama = Нреализ (S'U S"U...

Рисунок 12. Декомпозиция модели на подмножества состояний

Figure 12. Decomposition of the model into subsets of states

На каждый подобный переход могут приходиться десятки и сотни переходов модели на подмножестве состояний { S' } с высокими значениями вероятностей состояний. Соответственно, на подмножестве { S' } потребуется сгенерировать в десятки и сотни раз большее количество реализаций переходов.

Следовательно, если количество состояний модели N cocm ~ 50, то количество реализаций путем декомпозиции модели может быть снижено на два порядка.

Кроме того, возникает дополнительное удобство в построении логики алгоритмов моделирования. Достаточно иметь всего одну универсальную отлаженную модель, «элементарную ячейку», пригодную для любых состояний, и задавать в ней лишь вид и параметры исходящих потоков, а также требуемое количество сгенерированных переходов.

Снижение вычислительных затрат за счет объединения простейших потоков.

При реализации классического метода Монте-Карло любая единичная реализация перехода из некоторого состояния требует формирования случайных временных интервалов по жребию для всех исходящих из данного состояния потоков. Количество реализаций определяется потоком с минимальной интенсивностью.

То есть при объединении простейших потоков достигается выигрыш двух видов:

• •    собственно за счет сведения нескольких потоков в один;

• •    выигрыш, если простейшие потоки задают количество реализаций за счет малой интенсивности.

В первом случае можно принять предположение о том, что в модели около половины потоков являются простейшими. В этом случае и количество потребной генерации случайных величин сократится примерно вдвое. Однако следует отметить, что в количестве простых арифметических действий выигрыш не будет столь значителен, поскольку сокращается генерация наименее затратных по трудоемкости величин.

Второй аспект выигрыша может оказаться более существенным, в зависимости от конкретной модели. В целом оценку выигрыша можно принять равной 2–5-кратной по количеству реализаций.

Итак, с учетом того, что генерация случайных величин включает в себя не менее 10 простых операций, выигрыш по трудоемкости алгоритма приведения модели к марковской составит от 10 Н сост до 100 Н сост в простых операциях относительно имитационного моделирования.

Тогда, на основе (24) и с учетом (13) для последующего решения марковской модели, общая оценка трудоемкости метода составит:

F a ( П ) = О ^ 10 8 N cocm ² + - N cocm ² J«

• *    О ( 10 8 N cocm ² ) ;                        .    (28)

F ( n ) = nf 5 - 10 4 N _m + ^- NJ I . a                    сост       сост

Верхняя оценка трудоемкости предложенного метода приближается к нижней оценке для имитационного моделирования. Нижняя оценка близка к линейной зависимости от числа состояний при малом их количестве и может приближаться к квадратической зависимости при N cocm > 10 4 .

Можно также видеть, что решение СЛАУ привносит незначительный вклад в затратность метода. Снижение затрат в случае единственности рекуррентного потока исходящего из некоторого состояния модели.

Достаточно принять интенсивность изоморфного простейшего потока X равной интенсивности рекуррентного потока Х=Л. Это обусловлено сходимостью среднего значения временного интервала пребывания системы в данном состоянии tcp к его математическому ожиданию m(t) при достаточном количестве реализаций, независимо от вида и формы закона распределения вероятностей.

Существенное упрощение оптимизации параметров системы на модели.

При оптимизации параметров системы в каждом эксперименте достаточно пересчитать интенсивности потоков только для одного состояния. Для прочих состояний их представление в изоморфной модели не изменится.

Тогда в (25) в первом члене следует положить N cocm = 1 и выражения переходят в

10 8 + з N cocm ² J ;

5 - 10 4 + ^- N J ) сост

F a (n ) = 9 ^f- N cocm ² J , (30)

что соответствует марковским моделям.

Таким образом, разность оценок (25) и (26) позволяет утверждать, что синтез с декомпозицией модели и применением изоморфного марковского представления снижает вычислительные затраты на каждый последующий эксперимент в десятки тысяч раз как минимум, и в миллионы раз тогда, когда случайные величины имеют сложные для имитационного моделирования законы распределения вероятности.

Обсуждение

Рассмотренный подход к моделированию динамики сложных систем показывает, что существует проблема получения оценок вероятностей состояний для случая, когда распределения вероятностей в потоках событий неэкспоненциальны. Эта проблема сводится, главным образом, к существенным вычислительным затратам. Оценки трудоемкости алгоритмов показывают, что с возрастанием количества состояний и переходов модели временные показатели моделирования достаточно быстро становятся неприемлемыми. Даже с применением современных компьютеров построение и исследование модели с количеством состояний более 20 становится нетривиальной и далеко не всегда корректно решаемой задачей.

Предложенный и обоснованный в статье метод моделирования опирается на фундаментальные положения теории подобия и изоморфизм различных моделей динамики одного объекта. Сочетание элементов аналитического и имитационного моделирования, применяемых на различных этапах декомпозиции модели и последующего синтеза ее изоморфного представления, позволяет значительно снизить затраты на оценку стационарных значений вероятностей состояний системы.

откуда следует