Оценка творческого потенциала конструктора на основе понятия красоты механических и алгебраических структур

должен быть понятен всем субъектам тестирования. Необходимы также меры и шкалы для получения объективной оценки. Анализируя различные подходы в этой области, автор пришел к выводу, что таким критерием может служить понятие красоты. Это, на первый взгляд, неожиданное решение имеет под собой весомое основание. С одной стороны, понятие красоты сугубо индивидуальное, личностное, некая «категориальная интуиция» [1], свойство человеческого мозга. С другой стороны, многие ученые рассматривали красоту как непременный фактор в своих работах. «Едва ли кто-нибудь из нематематиков в состоянии освоиться с мыслью, что цифры могут представлять собой культурную или эстетическую ценность или иметь какое-нибудь отношение к таким понятиям, как красота, сила, вдохновение. Я решительно протестую против этого костного представления о математике» [2], - говорил Н. Винер в своей работе «Я математик». Известно другое крылатое выражение, высказанное А.Н. Туполевым: «Некрасивые самолеты не летают».

Выбор объекта оценки. Известен «Принцип 100-процентной эффективности математики», по которому «Для любой реальности и любой наперед заданной точности существует математическая структура, которая описывает эту реальность с этой точностью, и, обратно, для любой математической структуры и любой точности существует реальность, которая описывается этой структурой с этой точностью» [5]. Наглядное представление структур [3] позволяет эффективно их исследовать, получать новые знания о них, находить требуемые закономерности. Наиболее четко характеристика эстетической привлекательности математического объекта дана Г. Биркгофом: M=O/C, где M — мера красоты объекта, O — мера порядка, а C — мера усилий, затрачиваемых для понимания сущности объекта [4].

Для целей работы объектами оценки были выбраны различные алгебраические структуры, визуально представленные с использованием отношений наглядности [3]. Эти наглядные структуры обладают зеркальной, переносной, поворотной, орнаментальной симметрией, антисимметрией, в них присутствуют соотношение общего и частного, самоподобие, подструктуры и т.д. Критерием правильности выбранных наглядных отношений являются полученные новые знания о структурах и их применение на практике, поэтому использование данных структур в качестве эталонных объектов выглядит достаточно справедливо.

Выбор субъекта оценки. Были выбраны индивидуальные и коллективные субъекты оценки. Все тесты проводились анонимно. Задания предлагались студенческим группам, сотрудникам организаций. Разные группы имели различную подготовку, различную предметную область деятельности. Общим для всех было то, что никто из них не изучал высшую алгебру, не знаком с теорией решеток, поэтому влияние математического образования было минимальным. С другой стороны, это внесло некоторые сложности, поскольку формулировка критерия должна была быть понятна всем. Поэтому текст тестового задания был ближе к бытовому, чем к научному. Задание №1 звучало так: «Соедините вершины прямыми ребрами, чтобы было красиво». Ключевая фраза: «чтобы было красиво» объяснялась так: «Исходя из вашего внутреннего понимания».

Тестовые задания и результаты. Использовались несколько заданий, которые предлагались трем различным группам, которые условно назовем {студенты 1 гр., студенты 2 гр., специалисты}. Для анализа использовались решетки L = ( L ( m , n ), с , ц ) слов m буквенного алфавита длиной не более n символов. Здесь L ( m,n ) - множество слов, ^с - отношение включения для L , Ц = ( Ц Ц 2 , Ц з , Ц 4 , Ц 5 ) - отношения наглядности [3] для L . В дальнейшем, для краткости запись L ( m,n ) будет означать L = ( L ( m , n ), с , ц ) . Пусть P ={ L (4,2), L (4,3), L (4,4)}- множество решеток, предъявленных для тестовых заданий. Пусть Q ={студенты 1 гр., студенты 2 гр., специалисты (3 гр.)} -множество групп субъектов. Тогда множество

всех испытаний состоит из элементов декартова произведения (p,q) е P х Q : p е P , q е Q . В случае L ( m,n ) мы ограничились испытаниями: ( L (4,3), 2 гр.); ( L (4,2), 1 гр.); ( L (4,3), 3 гр.); ( L (4,4), 1 гр.); ( L (4,4), 3 гр.).

На рис. 1a представлен оригинал L (4,3) для испытания №1, предъявленного студентам 2 гр. Это решетка упорядоченных слов 4-х буквенного алфавита длиной не более 3-х символов. Благодаря введению отношений наглядности д , решетка обладает рядом свойств,

которые характеризуют понятие «красота». Уровневые числа (1,1,2,3,4,4,5,4,4,3,2,1,1) симметричны. Количество ребер, находящееся между смежными уровнями, симметрично. Решетка разбивается на непересекающиеся подрешетки (рис. 1b, 1c, 1d). Сами подрешет-

ки упорядочиваются отношением включения. Количество вершин v ( m,n ) в произвольной решетке L ( m,n ) равно

	f m + n		m + n
v ( m , n ) =		=		, а	ребер
	V n 7		V m .

e ( m, n ) =

fm+n

V ⁿ

1 ^

• n =

fm + n - 1

V ^m 7

•m

Это далеко не все свойства, которые характеризуют рис. 1a.

После выбора ( L (4,3), 2 гр.) было сформировано изображение для тестового задания, представленное на рис. 2b. Здесь из рис. 2a удалены все ребра. Примеры характерных ответов представлены на рис. 2c и 2d. Задание следующее: «Соедините вершины прямыми ребрами, чтобы было красиво».

На рис. 2c понятие красоты связано с задачей соединить все вершины меньшим числом линий. На рис. 2b сделана попытка

соединить вершины параллельными линиями. Что примечательно, в первом случае использовались в основном кривые линии, во втором - прямые.

На рис. 3 результаты второго задания, для которого были представлены пронумерованные вершины решетки L (4,3), в соответствии с рис. 1a. Задание таково: «Соедините вершины ребрами в соответствии с нумерацией, чтобы было красиво».

Анализируя результаты, заметим следующее. Нумерация вершин позволило субъекту абсолютно точно воспроизвести логику изображения на рис. 3a. Субъект, предъявивший рис. 3b, возможно проигнорировал или не понял структурную нумерацию элементов. С точки зрения описанных выше критериев, рис. 3a красив и, как следствие, позволяет вычислить ряд характеристик решетки. Рис. 3b назвать красивым сложно.

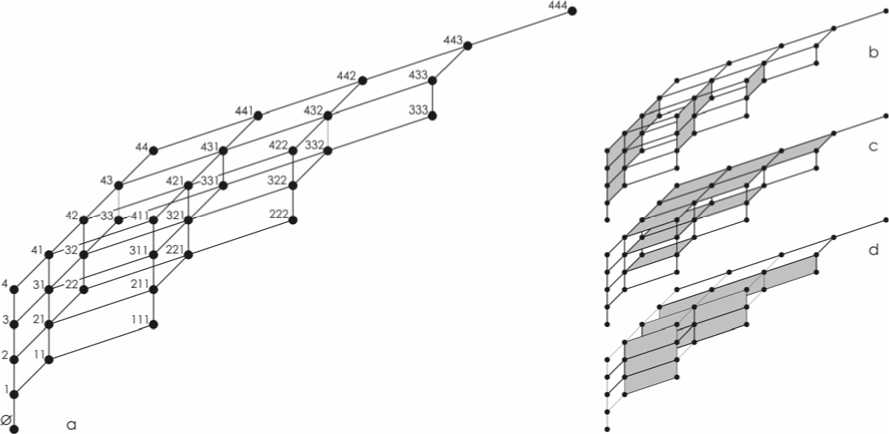
Рис. 1. Решетка L (4,3) слева и eё непересекающиеся подмножества 1b, 1c, 1d справа

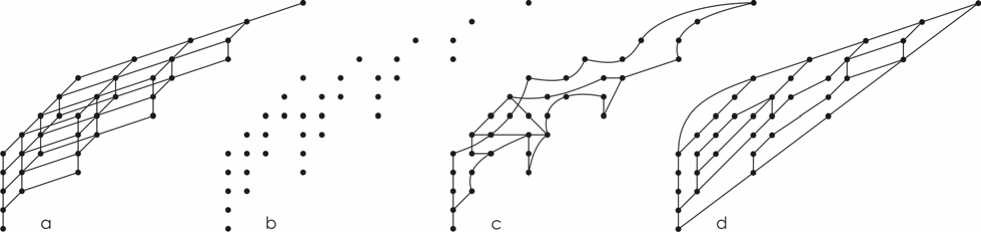
Рис. 2. Оригинал 2a, тестовое задание 2b и примеры решений 2c, 2d

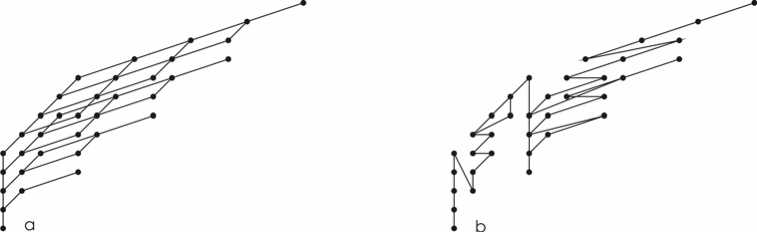
Рис. 3. Результаты выполнения второго задания

Рис. 4. Тестовое задание (L(4,2), 1гр) на рис. 4a и результаты 4b-4i

На рис. 4а представлено изображение для тестового задания. Это решетка L(4,2), у которой удалили все ребра. Отметим, что чем меньше количество вершин, тем больше результат совпадает с оригиналом. В частности, рис. 4е полностью совпадает с оригиналом. Во всех представленных рисунках, за исключением рис. 4с, имеется симметрия относительно центральной оси.

Общий подход к составлению теста позволяет произвести коллективную оценку субъектов путем объединения и пересечения ребер на графах. На рис. 5а представлены результаты такого объединения. Мы составляем коллективное решение объединением ребер всех изображений. Несмотря на то, что имеются отдельные несимметричные изображения, коллективное изображение обладает симметрией относительно центральной оси. Это наблюдение позволяет предположить, что интегрированные показатели стремятся к некоторому устойчивому состоянию, характеризующему группу субъектов. На рис. 5b, наоборот, представлены ребра, отсутствующие на рис. 5a. Из рис. 5b видно, что в нем отсутствуют ребра, удаленные друг от друга. Это своего рода «рационализм» в групповом понятии красоты. Соединяются только близлежащие вершины. Рис. 5a и 5b повернуты на угол atg(2).

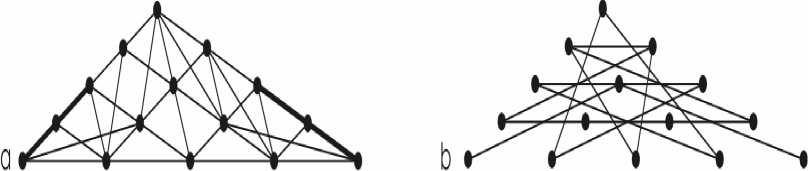
Рис. 5. Объединение 5a и пересечение 5b заданий группы

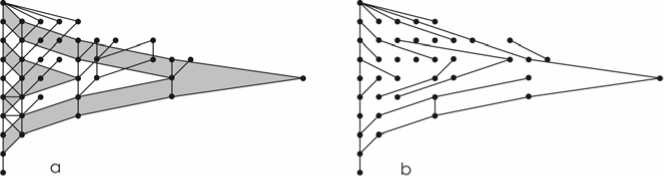
Рис. 6. Оригинал P (10,µ) и пример теста

На рис. 6a представлен фрагмент решетки делителей P ( n , µ ). Здесь n =10. Наглядные отношения µ такие же, как и для L ( m,n ). Решетка P (10, µ ) упорядочивает и наглядно изображает все возможные разбиения числа n =10. Количество разбиений p (10)=42. Решетка P (10, µ ) симметрична относительно центральной оси. В ней можно выделить подрешетки, упорядоченные отношениями включения (обозначены серым цветом). На рис. 6b показаны ребра, общие для оригинала и результата тестирования. Числовой мерой оценки схожести может служить отношение числа совпадающих ребер для каждого уровня к числу ребер оригинала. Для оригинала количество ребер равно (5,7,9,12,9,5,4,2,1,). Количество совпадающих ребер соответственно (5,4,6,5,6,,4,4,2,1). Общий процент совпадения 37/54=69%. (На рис. 6a указаны не все ребра оригинала).

Анализ результатов. Как отмечалось ранее, задача данной работы – оценить способность субъекта воспринимать структуру, ее целостность. Такие качества необходимы для проектирования систем, устройств, рассчитанных на длительный жизненный цикл. С этой целью мы предлагали для тестирования объекты, в которых «…симметрия является наиболее общим и наиболее мощным способом изучения структур; более того, симметрия какой-либо структуры, в свою очередь, имеет свою собственную структуру, которая также может изучаться с помощью симметрии и т.д.» [5]. Критерием было выбрано понятие красоты, поскольку «…симметрия обозначает тот вид согласованности отдельных частей, которое объединяет их в единое целое. Красота тесно связана с симметрией» [6, стр. 35]. Анализируя полученные от субъектов результаты, можно сделать следующие выводы.

Понятие красоты связано с понятием симметрии и асимметрии. Это хорошо видно по заданию (L(4,2), 1гр.).

Понятие красоты связано с понятием рациональности. Никто не изображал лишних дуг, несмотря на отсутствие каких либо ограничений на их количество. Характерным объяснением этому является рис. 5b, где изображены дуги, отсутствующие в полученных от субъектов заданиях.

Понятие красоты, как правило, не связано с понятием упрощенности. Все задания можно было выполнить путем соединения вершин только вертикальными и горизонтальными ребрами. Практически никто не воспользовался этой идеей, хотя она была на поверхности.

Многие тесты показали, что интуитивное нахождение самоподобных элементов структур, соотношение целого и его частей в исходном изображении не является приоритетом в понимании красоты. Неожиданными результатами тестирования было одушевление некоторых изображений. Субъекты приписывали названия: это «елочка», «ежик» и т.д. Несмотря на то, что была четко поставлена задача об использовании только прямых ребер, некоторые субъекты не смогли отказаться от изображения кривых ребер, поскольку ряд вершин визуально казались им лежащими на дуге.

Подсчет характеристик испытаний методами наглядного комбинаторного анализа. Подсчет числа вершин и ребер оригинала и результатов – один из методов числовой оценки. При подсчете обобщенного результата испытаний группы вхождение ребер в результирующей решетке имеет нечеткий характер. Иногда требуется решить перечислительные задачи теории графов. В частности, подсчитать количество связных помеченных графов на n вершинах, а также число помеченных связных графов каждой компоненты разбиения, если граф на n вершинах не связен. Первая задача решается путем вычисления коэффициентов производящей функции [7, с. 138] по формулам (1), (2). Последовательность числа графов представлена в EIS A001187 [8].

10				1
9				10
8				45
7				120
6			1	205
5			6	222
4			15	125
3		1	16
2		3
1	1
n	2	3	4	5

Таблица составлена с использованием формулы (3) для каждого элемента разбиения числа n .

Г к - 1 A

K - 2 Yc

G (5) = П ^ c

i = 0

j

j = i

V c i 7

f(S,1,1).

^K ( z ) = In 1 + У ²

n > 1

V

n

•

zn '

n!

.

K ( n ) = 2

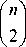
2 ^

n

\

I "  I ( n₇

I 1 l + l ²

2V 2 7 V 2

V " 1 , ⁿ 2 7

+ ...,

где n 1 + n 2 +…+ n k = n и 0< n j < n . Для второй задачи предложен метод, основанный на наглядном комбинаторном анализе [3]. Результат для первых n =2,3, 4,5 вершин и k =1,2,…10 ребер представлен в таблице, которая продолжается вправо вверх, используя значения предыдущих столбцов.

В (3) S – разбиение числа, записанное в строковом виде. Например, разбиение ( c 1, c 2, c 3, c 4) =3+3+2+2 записывается как S =( s 1 , s 2 , s 3 , s 4 ) = «3322». В столбцах таблицы представлены значения для количества связных графов с k ребрами n вершинами. Общее количество связных ориентированных графов равно сумме всех значений соответствующего столбца n . Функция f ( S ,1,1) подсчитывает произведение факториалов количества вхождений одинаковых символов строки S . В нашем примере f ( S ,1,1)=2!*2!=4. Чтобы получить очередной столбец в таблице, все G ( S ) умножаются на соответствующие значения предыдущих столбцов и складываются. Результат вычитается из количества сочетаний C ( K,k ), где К = С ( n ,2).

Алгебраические модели некоторых механических конструкций. Возьмем характеристические уравнения вида х^р ( х – 1) – 1=0, которые порождают обобщенные последовательности Фибоначчи [9], задаваемые рекуррентной форму-лой F n ⁽ p) = F n - 1⁽ p) ⁺ F n - 2⁽ P)• В [3] ^описана методика построения наглядных алгебраических объектов, заданных целочисленными последовательностями. Такие объекты могут быть с точностью до изоморфизма отображены на механические конструкции, что соответствует упомянутому выше принципу (закону) 100%-ной эффективности математики. Наглядная алгебраическая модель предоставляет новые возможности для исследования

механических, эксплуатационных, экономических и.т.п. свойств самого объекта.

Рассмотрим алгебраическую структуру, изображенную на рис. 7a, построенную на основе уравнения х2(х – 1) – 1=0, и напоминаю- щую контуры морского судна. Множества вершин в каждой затененной области по аналогии назовем отсеком. На рис. таких отсеков 18.

Рис. 7. Конструкция 7a на основе уравнения x2(x-1)-1 и соединение конструкций – 7b

Данная конструкция обладает рядом замечательных свойств. В частности, длина каждого отсека, измеряемого количеством вершин, равна обобщенному p-числу Фибоначчи с номером, соответствующим номеру отсека. Вес (множество вершин) каждого отсека равно 2 ■ Fn+2 ( p). Длина всей конструкции оп- ределяется как удвоенная сумма

S n ( p ) = ■ F n + p + 1 ( p ) ряда p -чисел Фибоначчи.

Для соединения, в том числе и механическим способом, двух конструкций, задан- ных характеристическими уравнениями с параметрами p1 и p2, нужно решить в целых чис- лах относительно n1  и n2 уравнение

Sn 1(P1) = Sn 2(P2) ■ Поскольку длина вы- ражается через числа Фибоначчи, то заменим сумму на Fn1+p1+1(p1)= Fn2+p2+1(p2). Одним из решений является F18(4)=F13(2). Соединение изображено на рис. 7b.

Для замкнутой формы записи классических ( p =1) чисел Фибоначчи используется формула Бине:

F n

; (фп+ф-n )№, 'ХФ" - фn )/V5, n - неч.

n - чет.,

где - ф число Фидия. Данную формулу, опре- деленную для целых чисел, используем для вещественных чисел. Получим график, изображенный на рис. 9, по форме напоминающий крюк. Используя определение чисел Fn=Fn-1+Fn-2, соединим прямыми линиями соседние целочисленные точки. (График нечетных чисел мы сместили на 10 единиц вверх). Есть основания полагать, что механическая конструкция, созданная по предлагаемой модели, позволит выдерживать оптимальную нагрузку при минимальном количестве элементов и их соединений.

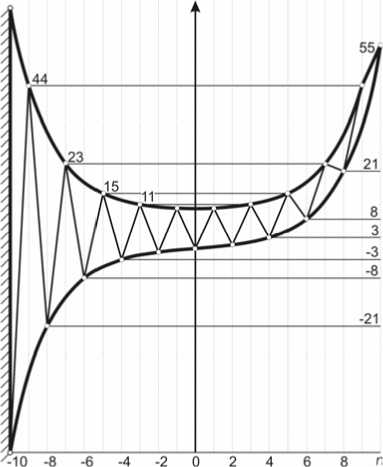
Рис. 8. Крюк Фибоначчи

Отметим, что моделирование и задание механических конструкций при помощи алгебраических объектов и систем в первую очередь определяет рациональные пространственные координаты элементов конструкции, что позволяет с высокой точностью автоматизировать и роботизировать все процессы производства и сборки, свести к минимуму технологические погрешности. Потенциально имеется более высокая технологичность сборки и изготовления элементов конструкции, которые создаются из типовых блоков, обладающих фрактальными свойствами. Упрощаются экономические расчеты.

Достаточно часто на практике встречаются технические объекты, свойства которых проектировщик осознанно или интуитивно сопоставляет свойствам алгебраических структур. На рис. 9 показан летальный аппарат, его проекция и соответствующая решетка L (8,2).

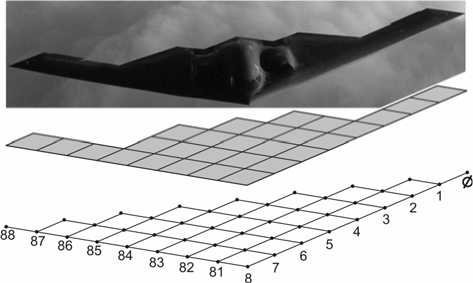
Рис. 9. Изображение, его проекция и решетка L (8,2)

Выводы:

• 1.    Алгебраические методы позволяют естественным образом присвоить всем элементам уникальные номера и электронные адреса. Появляется возможность управлять всеми узлами и осуществлять пространственную трансформацию конструкции. При наличии в узлах датчиков состояния с уникальными номерами возможно создание распределенных систем технической диагностики.

• 2.    Любые сложные системы проектируют и эксплуатируют люди. Конечная цель работы – придать процессу проектирования системный подход, помочь конструктору отойти от двумерного восприятия действительности.

• 3.    Проведенные в рамках статьи эксперименты говорят, что мир не всегда воспринимается структурно. В связи с этим актуальна задача понимания восприятия субъектом

окружающей действительность и соответствующая адаптация учебного процесса, для выявления творческого потенциала конструкторов.