Оценка участия синхронного генератора в демпфировании низкочастотных колебаний по данным синхронизированных векторных измерений

Настоящий этап развития энергетики характеризуется наличием соединенных относительно слабыми связями крупных концентрированных энергосистем, в состав которых активно включаются мощности распределенной генерации. Изменение состава генерации и структуры электропотребления приводит к уменьшению постоянных инерции элементов энергосистем, повышая чувствительность параметров режима энергосистемы в целом к небольшим возмущениям. В целях повышения управляемости энергосистем внедряется новое оборудование, оснащенное современными быстродействующими устройствами регулирования: асинхронизированные и синхронные генераторы, FACTS, накопители энергии. В результате ввода новых устройств помимо повышения управляемости режима в энергосистеме появляются также некоторые негативные свойства, проявляющиеся, в частности, в возникновении низкочастотных (0,1–3,0 Гц) общесистемных колебаний ее режимных параметров.

Низкочастотные колебания (НЧК) параметров электрического режима при электромеханических переходных процессах в энергосистемах обычно возникают в результате таких ситуаций, как:

• •    понижение или повышение частоты электрического тока из-за возникшего резкого изменения мощности генерации и потребления (нагрузки потребителей) в энергосистеме;

• •    асинхронный режим работы отдельных частей энергосистем;

• •    разделение ЕЭС;

• •    ведение режима вблизи предела по статической устойчивости в сечениях;

• •    неправильная настройка системных регуляторов (АРВ, АРСВ).

По своей природе НЧК – это нелинейные и нестационарные колебательные процессы, представляющие собой наложение нескольких составляющих движения (в том числе и низкочастотных) вращающихся масс в энергорайоне или узле, оказывающих взаимное влияние.

Резонансные (собственные) частоты энергосистемы и частоты электростанций, входящих в энергообъединение, сугубо индивидуальны, но в каждой из них проявляются различные низкочастотные составляющие, соответствующие взаимному движению различных концентрированных частей или целых энергосистем друг относительно друга, а также собственные частоты генераторов станций [1].

Незначительные колебания синхронных генераторов (СГ) станций происходят практически всегда из-за непрерывно возникающих небалансов потребляемой и генерируемой мощностей, что выражается в малых изменениях частоты системы в энергорайонах. Эти колебания легко демпфируются и не вызывают опасений. Но при возникновении значительных небалансов мощности в энер- госистемах могут возникать циклические изменения частоты с амплитудами более 0,05 Гц. В таких ситуациях крайне важным становится мониторинг эффективности демпферных свойств каждого генератора, которые в значительной степени определяются настройками применяемых системных регуляторов.

Оценка участия синхронного генераторав демпфировании НЧК

В качестве меры демпферных свойств генератора целесообразно принять величину энергии, затраченной генератором на противодействие скольжению ротора относительно частоты системы – синхронизирующей энергии на интервале времени переходного электромеханического процесса.

Для оценки способности СГ сохранять синхронный режим при отклонении угла нагрузки синхронной машины 9 от некоторого установившегося значения 9₀ на некоторую величину Д9 используют синхронизирующий момент дМ/д9 и, соответственно, удельную синхронизирующую мощность дР/д9 [2].

Величина активной синхронизирующей энергии СГ в течение цикла НЧК (при |/_p(t) —/_н| < Д/ Цоп.откл. ) определяется выражением

• ^ сц = к. ц РмЛ .П, (1) " нц

где И С _ц - синхронизирующая энергия в течение цикла НЧК;

• « нц», «кц» – начало и конец цикла, соответственно;

P_cм(t) - синхронизирующая мощность в момент времени t .

Тогда синхронизирующая энергия на интервале времени переходного электромеханического процесса определится как сумма И С _ц всех циклов колебаний.

В гидрогенераторах и турбогенераторах большой мощности КПД может достигать значений 0,97–0,99 [2].

Если пренебречь магнитными потерями и электрическими потерями в обмотке якоря, то электромагнитную мощность можно принять равной активной мощности генератора Р_эм = Р г [2] и при наличии прямых измерений активной мощности и угла нагрузки генератора можно определить удельную синхронизирующую мощность P_cм(t) для любого момента времени:

P cM (t) = дР эм (Р)/д9(Р). (2)

При правильной настройке системных регуляторов Рсм всегда препятствует изменению частоты системы, прикладывая синхронизирующий момент, действуя на уменьшение скольжения Д/с-р.

Влияние автоматических регуляторов скорости вращения турбины на Рсм(0 определяется отклонением /p(t) от номинального значения ЦрЮ-ГнУ Если |/р(()-/н| <ДЛц,п откл не вы- ходит за границы зоны нечувствительности, механический момент на валу СГ Мт (t) можно считать постоянным и не влияющим на Pcм(t). В противном случае его влияние может оказаться существенным.

Влияние АРВ СГ проявляется через изменение Р э _м (t) и может быть определено по измерениям тока возбуждения 7 ^ (t), а также векторов напряжения U_r(t) и тока I_r(t) статора: —    —

• / _^(t)^U г (t)•7 г (t)^P эм (t).             (3)

Для определения значений удельного синхронизирующего момента и удельной синхронизирующей мощности, соответствующих режиму работы синхронной машины в момент времени t , необходимо значение угла нагрузки синхронной машины.

Рассмотрим способы определения угла нагрузки синхронной машины для трех случаев состава непосредственно измеряемых (контролируемых) параметров регистраторами системы мониторинга переходных режимов (СМПР) на генераторе.

Способ 1

Для синхронной машины, работающей параллельно с системой, имеются измерения и полученные только из них следующие параметры:

• •    напряжение фаз обмотки статора ^и а , ^и Ь , ^U C ;

• •    ток фаз обмотки статора i_a,i_b,i_c ;

• •    фазовый сдвиг между напряжением и током фазы обмотки статора ф_а, ф_Ь, ф_С;

• •    напряжение обмотки возбуждения и ^ ;

• •    ток обмотки возбуждения i ^ ;

• •    угловое положение ротора;

• •    частота напряжения системы /_С;

• •    синхронная электрическая угловая скорость вращения поля статора ю_с = 2л/_с;

• •    электрическая угловая скорость вращения ротораю;

• •    угол нагрузки синхронной машины 9.

Значение угла нагрузки синхронной машины 9 может быть определено путем непосредственных измерений, либо используя интегрирование разности мгновенных значений электрической угловой скорости вращения ротора ю и синхронной электрической угловой скорости вращения поля статора (частота системы) [2]:

• 9    = ]> - ЮсЖ                (4)

Для этого случая удельная синхронизирующая мощность Рсм (t) для любого момента времени определяется по формуле (2).

Кроме того, при таком составе прямых измерений возможно:

• •    определить значение полного индуктивного сопротивления якоря синхронной машины ^ i = (^ а + ^ а ), соответствующее режиму работы в текущий момент времени и его составляющие:

Электромеханические системы главное индуктивное сопротивление фазы обмотки якоря Ха, индуктивное сопротивление рассеяния фазы обмотки якоря Ха, а также полное индуктивное сопротивление по продольной оси Ха и полное индуктивное сопротивление по поперечной оси Хq;

• •    оценить влияние автоматического регулирования возбуждения конкретной синхронной машины на ее работу параллельно с сетью в текущий момент времени.

Способ 2

Для синхронной машины, работающей параллельно с сетью, выполняются измерения следующих параметров:

• •    напряжение обмотки статора и_а, и_ь, и_с;

• •    ток обмотки статора i_a, i_b, i_c ;

• •    фазовый сдвиг между напряжением и током обмотки статора ф_а, ф_ь, ф_с;

• •    напряжение обмотки возбуждения и ^ ;

• •    ток обмотки возбуждения i ^ ;

• •    частота напряжения системы /_с.

При малых колебаниях ротора отклонения угла нагрузки синхронной машины относительно начального значения малы, тогда можно считать, что sin(49) = 49 = 9 — 9₀. В этом случае допустимо при определении угла нагрузки использовать экспериментальные или проектные параметры (номинальные значения напряжения и тока, индуктивное сопротивление Потье Х_р, индуктивное сопротивление рассеяния фазы обмотки якоря Х_а и др.) и характеристики (холостого хода, -фазного короткого замыкания и др.).

Тогда значение угла нагрузки синхронной машины можно определить с применением уравнений, соответствующих векторной диаграмме синхронной машины [2]:

Usin(9) = Х_Ч1_Ч — RI_d,                     (5)

Ucos(9) = E_f — Х_й1_й — RI q ,               (6)

где U - фазное напряжение на выводах обмотки якоря;

• 0    - угол между вектором ЭДС Е ^ и вектором U ;

• Е ^ - ЭДС возбуждения, индуцируемая в фазе обмотки якоря полем взаимоиндукции от МДС возбуждения;

Х_q , Х_й - полное индуктивное сопротивление по поперечной оси и полное индуктивное сопротивление по продольной оси, соответственно;

I_q = Icos(e), I_d = Isin(e) - поперечная и продольная составляющие вектора фазного тока обмотки якоря I = I_d + jI_q ;

• в    = 9 + ф - угол между вектором Е ^ и вектором I;

• ф    - угол между вектором U и вектором I;

• R    - активное сопротивление фазы обмотки якоря;

тогда

• 9    = arctg f^C^Y             (7)

\E f -XdU-RlqJ                       ^{V 7}

Учет насыщения магнитной цепи может осуществляться для известных значений тока нагрузки и тока возбуждения в текущий момент времени.

Неопределенность значения угла нагрузки синхронной машины будет зависеть от:

• •    интервала интегрирования мгновенных значений напряжения обмотки статора, тока обмотки статора, тока обмотки возбуждения;

• •    гистерезиса (неоднозначности) зависимости ЭДС холостого хода и, как следствие, напряжения и тока статора от значения тока обмотки возбуждения.

Способ 3

Для синхронной машины, работающей параллельно с сетью, выполняются измерения следующих параметров:

• •    напряжение обмотки статора и_а, и_ь, и_с;

• •    ток обмотки статора i_a,i_b,i_c ;

• •    фазовый сдвиг между напряжением и током обмотки статора ф_а, ф_ь, ф_с;

• •    частота напряжения системы /_с.

В этом случае значение угла нагрузки синхронной машины приближенно определяется по формуле (7), считая значения параметров постоянными и не зависящими от нагрузки и тока возбуждения.

Неопределенность значения угла нагрузки синхронной машины зависит от:

• •    интервала интегрирования мгновенных значений напряжения обмотки статора, тока обмотки статора, тока обмотки возбуждения;

• •    величины отклонения параметров синхронной машины для значений напряжения и тока нагрузки и тока возбуждения, соответствующих режиму работы синхронной машины в текущий момент времени, от значений, принятых неизменными.

Таким образом, определив угол нагрузки синхронной машины, по формуле (2) можно определить синхронизирующую мощность для любого момента времени. По зависимости PCM(t) можно оценить качество работы системных регуляторов.

В качестве практического примера оценивалось участие турбогенератора номинальной мощностью 800 МВт в демпфировании низкочастотных колебаний, произошедших во время технологического инцидента. Так как регистратором СМПР измерялись только токи и напряжения обмоток статора, расчеты выполнялись способом 3.

График активной мощности генератора Р г в данном инциденте приведен на рис. 1. На рис. 2 приведены полученные зависимости активной мощности генератора от угла его нагрузки 9 по одному циклу НЧК для указанных интервалов.

На интервалах по 10 секунд (8 циклов НЧК), обозначенных на рис. 1, определялись следующие величины:

Ргср- среднее значение мощности генератора;

Рис. 1. Колебания активной мощности генератора

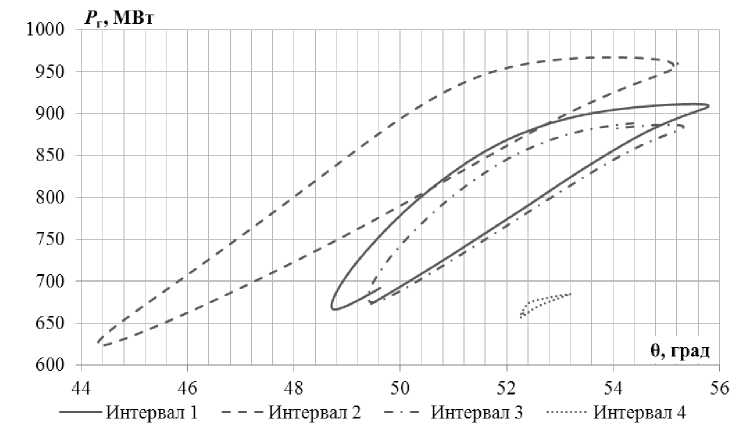
Рис. 2. Зависимость активной мощности от угла нагрузки генератора

Р_г^мин — ми ним ал ь н ое з на чение мощнос ти генератора;

Р_г^макс — ма кс им а л ьное з на че н ие мощнос ти г енератора;

9^ср- среднее зн аче н ие уг л а нагр уз к и ге не ратора;

9^мин- ми ним а л ьн ое з на че н ие у гл а на гр у з к и генератора;

9^макс - ма кс им а л ь ное з на чение у г л а нагр уз к и генератора;

^ синх.уд — с ре дн ее з на че н ие у де л ь н ой с ин х ронизирующей мощности;

Р сИИН.уд — м и ним а л ьн ое з на че н ие удел ь ной синхронизирующей мощности;

Р СИНХСуд — ма кс им а л ьное з на че н ие у де л ь ной синхронизирующей мощности;

Ре з у л ьта ты ра с че тов прив ед е ны в табл. 1.

Средняя удельная синхронизирующая мощность характеризует количество энергии, прилагаемое генератором на демпфирование колебательного процесса. Из табл. 1 видно, что наименьшая величина РсИНх.уд =26,15 МВт/град имела место при наибольшей амплитуде низкочастотных колебаний. После разгрузки генератора ее величина увеличилась до 34,82 МВт/град и перед затуханием достигла величины 41,06 МВт/град.

Оценка влияния допущений, принятых в способе 3, выполнена в среде MATLAB на модели двухрайонной системы, представленной в главе 12 «Power System Stability and Control» [3]. В качестве примера из работы были выведены PSS генераторов 1, 2, 4, в результате чего наблюдаются затухающие НЧК активной мощности генераторов амплитудой до 50 МВт и частотой 0,55 Гц. На рис. 3 приведен график НЧК активной мощности P г зафиксированные на генераторе 3. На рис. 4 приведена зависимость активной мощности Р_г генератора 3 от значений угла нагрузки генератора 9, полученных в результате измерения¹ (способ 1) и расчета (способ 3).

Результаты расчетов приведены в табл. 2.

Электромеханические системы

Таблица 1

Результаты анализа НЧК активной мощности турбогенератора

Интервал	И 1 (65с-7 5с )	И 2 (242с-252с)	И 3 (292с-302с)	И 4 (522с-532с)
P г ср,МВт	804, 5 3	835,08	798,59	670,76
P г мин,МВт	664, 1 6	610,13	674,95	654,57
P г макс,МВт	913, 4 7	970,99	890,66	684,73
θср, град	52,37	50,13	52,65	52,66
θмин, град	48,57	43,63	49,39	52,17
θмакс, град	55,90	55,50	55,57	53,21
МВт ср P синх. уд , град	36,60	26,15	34,82	41,06
МВт мин P синх. уд , синх. уд град	–5,33	–22,40	–0,95	–12,69
МВт макс P синх. уд , синх. уд град	94,92	49,12	94,89	131,78

0,00     2,50     5,00     7,50     10,00    12,50    15,00    17,50    20,00

Рис. 3. Колебания активной мощности генератора 3

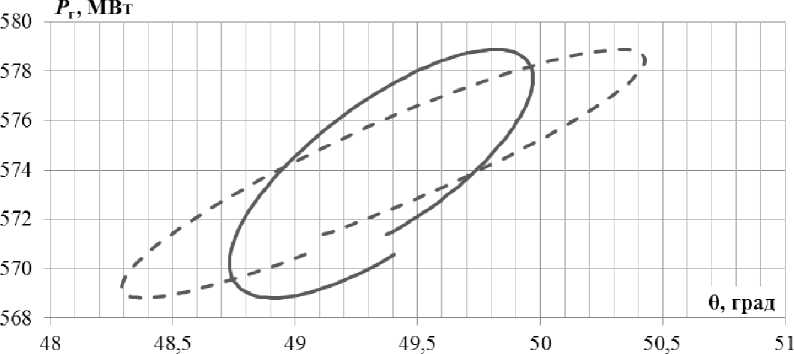
Способ 1--Способ 3

Рис. 4. Зависимость активной мощности генератора 3 от угла нагрузки генератора

Из табл. 2 видно, что допущения, принятые в способе 3, для модели приводят к увеличению амплитуды колебаний угла нагрузки генератора и снижению удельной синхронизирующей мощности. В то же время характер процесса при этом сохраняется, что позволяет выполнить только оценочный анализ.

Необходимо отметить, что без детальных экспериментальных исследований на реальных генераторах и адекватной физической модели корректно оценить погрешности, вносимые за счет приня-

Таблица 2

Результаты анализа НЧК активной мощности генератора 3

Pгср, МВт Pмин МВт Pмакс МВт θср, град θмин, град θмакс, град ср синх. уд, МВт/град мин Pсинх. уд , МВт/град макс Pсинх. уд, МВт/град Способ 1 574,07 568,82 578,88 49,38 48,73 49,97 8,06 –30,13 38,90 Способ 3 49,39 48,29 50,43 5,42 –25,87 38,07 тых в моделях допущений, не представляется возможным. Тем не менее, характер и тенденции происходящих процессов представляются достаточно наглядными.

Заключение

• •    В данной статье приведены способы определения угла нагрузки синхронной машины в зависимости от состава имеющихся измерений параметров электрического режима синхронного генератора.

• •    Принимая электромагнитную мощность равной активной мощности генератора и при наличии прямых измерений активной мощности и угла нагрузки генератора можно определить величину удельной синхронизирующей мощности для любого момента времени.

• •    Для корректной оценки погрешности, вносимой за счет принятых допущений при отсутствии измерения угла нагрузки генератора, необхо-

• димо выполнить экспериментальные исследования на реальных генераторах и адекватной им физической модели.

• •    По величине траектории удельной синхронизирующей мощности на циклах НЧК можно выполнять оценку качества работы системных регуляторов.