Оценка уровня оптимальности распределения накопленной деформации в поковках, изготавливаемых в открытых штампах

Введение. Современный уровень организации кузнечно-штамповочного производства поковок ответственного назначения определяется требованиями, предъявляемыми не только к сокращению сроков разработки технологических процессов, но и к определению достоверно эффективных технологических схем штамповки, заранее ориентированных на формирование заданных эксплуатационных свойств изделий.

Последнее направление, определяемое геометрической сложностью штампуемых поковок ответственного назначения, чаще всего обеспечивается применением многопереходных схем штамповки с достаточно сложными промежуточными формами. Одним из примеров такого технологического решения является схема применения заготовительных и черновых переходов штамповки, разработанная по методике достаточно давней зарубежной работы [1], ориентированной на штамповку поковок Н-образного поперечного сечения (рис.1, а-в ). В ней (рис.1, г ), как показы-

Рис. 1. Схема штамповки поковки спроектированная по рекомендациям работы [1] в заготовительном (а), черновом (б) и чистовом (в) ручьях, и распределение накопленной деформации в сечении поковки ( г )

вают результаты выполненного численного моделирования процесса штамповки методом конечных элементов (МКЭ) [2], достигается возможность существенного снижения неравномерности деформированного состояния в плоскости рассматриваемого сечения поковки в сравнении с традиционными производственными вариантами её штамповки в один и два технологических перехода (рис. 2).

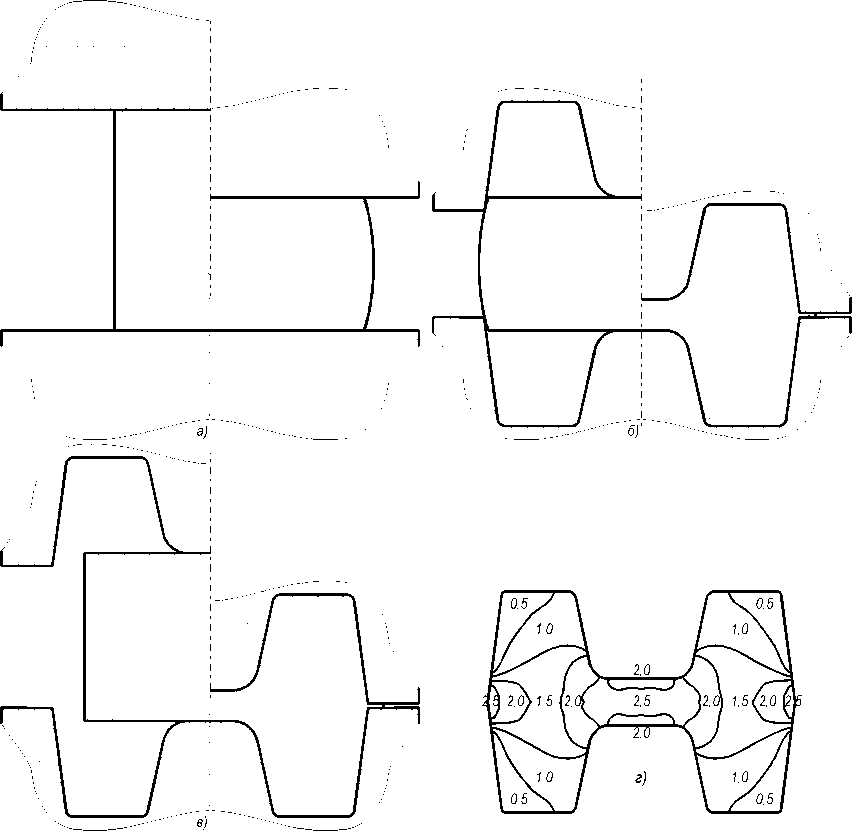
Рис. 2. Схемы штамповки поковки за два перехода ( а,б ) с предварительной осадкой заготовки ( а ) или без неё – за один переход ( в ) и распределение накопленной деформации в сечении поковки ( г ) для варианта ( в )

Общим недостатком рекомендаций, аналогичных рекомендациям работы [1], является то, что они при достаточно высоком уровне получаемых результатов определяются низкой универсальностью предлагаемых методик, ориентированных на конкретные формы поковок. В связи с этим в настоящей работе представлены результаты подхода, отличающегося большей универсальностью и основанного на процедуре многошаговой оптимизации процессов объёмной штамповки, реализованной посредством метода обратной прогонки динамического программирования [3]. Оптимизационная методика базировалась на результатах численного моделирования, реализованного методом граничных элементов (МГЭ) [4] посредством постадийного решения обратных задач формоизменения [5]. Эти данные отражены на рис. 3.

При этом, как известно из теории динамического программирования и видно из схемы многошаговой оптимизации (см. рис.3,в), подобный подход отличается повышенной сложностью реализации, связанной с большим объёмом расчётных действий. С другой стороны, не следует исключать и возможность получения результата, близкого к оптимальному по менее сложной технологической схеме штамповки. Поэтому для эффективной организации исследований процессов объёмной штамповки, по крайней мере на начальных этапах проектирования, необходима система не сравнительной, а обобщённой оценки уровня соответствия разработанного технологического решения преследуемой проектной цели.

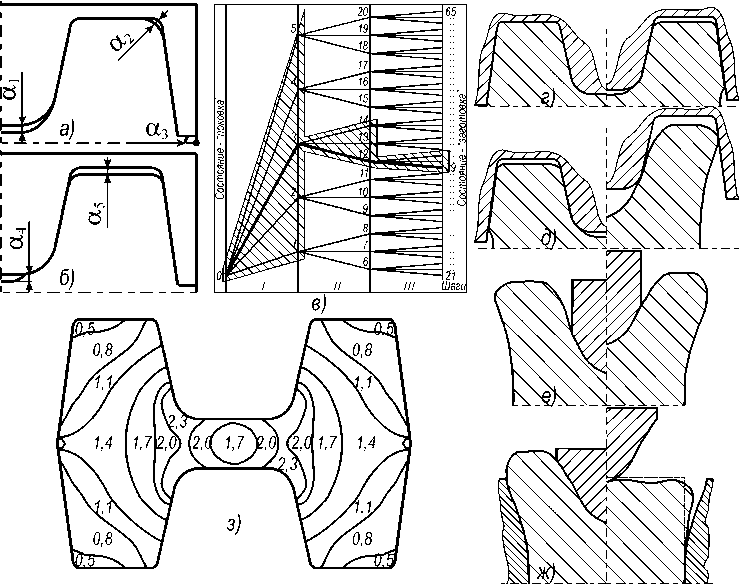
Рис. 3. Результаты применения процедуры многошаговой оптимизации, основанной на методе обратной прогонки динамического программирования, реализованном МГЭ: а, б – управления первого шага; в – схема многошаговой оптимизации; г-ж – оптимальная схема формоизменения в чистовом ручье на последней ( г ) и предпоследней ( д ) стадиях, в черновом ( е ) и заготовительном ( ж ) ручьях; з – распределение деформации, полученное МКЭ

В связи с этим в дополнение к реализованному оптимизационному подходу предложена методика оценки уровня оптимальности распределения деформированного состояния в поковках, позволяющая по результатам предварительного численного (МКЭ, МГЭ) или физического моделирования определять необходимость введения более сложных схем штамповки поковок.

Теоретический анализ. Учитывая результаты работы [6], в качестве целевой функции, определяющей неравномерность распределения накопленной деформации, использовали параметр [5, 7, 8]

n

∑ I ε _ср - ε _i I ⋅ S i

J = ^{i = 1} n ,                                                 (1)

∑Si i=1

где ε i и S i – степень деформации на произвольном ( i -м) участке сечения и площадь этого участка; ε ср – средневзвешенное по площади значение степени деформации по сечению поковки.

Реализация расчётов ориентирована на управление схемой заполнения чистового ручья посредством определения предшествующих заготовительных форм, при которой выражение (1) принимает минимальное значение:

J ^ min .                                      (2)

Отличительные особенности применяемой методики многошагового оптимизационного определения переходных форм штамповки состоят в достаточно широком диапазоне вводимых управлений [5, 8], применении алгоритма снижения размерности оптимизационной задачи – «киевский веник» Михалевича – Шора [9] и реализации решений обратных постадийных задач формоизменения по алгоритму реверсивного нагружения [10, 11] прямым методом граничных элементов [4].

Методика расчётов. Представление об управлениях на первом расчётном шаге, начатом от готовой поковки, отражающем схему заполнения чистового ручья металлом заготовки, можно составить по рис.3 ( а,б ) и табл.1.

Таблица 1

Варианты комбинаций управлений первого шага оптимизации

Варианты	1	2	3	4	5
Комбинации вводимых управ-	α 1 ≠ 0	α 1 = 0	α 1 ≠ 0	α 1 = 0	α 1 ≠ 0
лений	α 2 = 0	α 2 = 0	α 2 = 0	α 2 ≠ 0	α 2 ≠ 0
	α 3 = 0	α 3 ≠ 0	α 3 ≠ 0	α 3 ≠ 0	α 3 = 0
	α 4 = 0	α 4 ≠ 0	α 4 = 0	α 4 = 0	α 4 = 0
	α 5 ≠ 0	α 5 = 0	α 5 ≠ 0	α 5 = 0	α 5 = 0
J расч.	0,1892	0,2096	0,1636	0,2198	0,2045

В целях увеличения точности на каждом расчётном шаге результаты расчётов обратных задач формоизменения контролировали решением соответствующих прямых задач. Эти расчёты выполнялись МКЭ с использованием программы QForm [2].

Методика оценки уровня оптимальности распределения деформации. Разрабатываемое направление исследований определяет с единых позиций методику и систему первичного оценочного анализа оптимальности технологии штамповки поковок как по данным численного математического моделирования, так и по данным экспериментальных исследований, позволяя, например, при отсутствии данных о предшествующих вариантах изготовления конкретной поковки определять уровень предложенного технологического решения.

В качестве обобщенного геометрического признака формы поковки используется количественный критерий её сложности, рекомендуемый, например, работой [12, с. 158]:

S T = Φ П C П ,                                (3)

где Ф П = ( Р П /F_n )/( Р Ц /F_Ц ) - степень сложности сечения поковки (П ) относительно сечения описанной вокруг неё фигуры (цилиндра или параллелепипеда) (Ц ); С П = 2 R_ЦП / R_n - степень сложности поковки по конфигурации её сечения; P – периметры сечений; F – площади сечений; R П – наружный радиус поковки; R ЦП – абсцисса центра тяжести половины осевого сечения поковки.

Учитывая то, что в работах [1, 5–8, 10, 11] данных об оптимизации неравномерности деформации в поковках, полученных посредством численного и экспериментального моделирования в рамках методики обратной прогонки динамического программирования, недостаточно, результаты обобщённого анализа были дополнены результатами теоретического (главным образом в рамках метода прямой прогонки динамического программирования) и экспериментального оптимизационного исследований, выполненных другими авторами. Некоторые из анализируемых данных представлены на рис.4 и в табл.2.

В частности, в табл.2 представлен выборочный анализ сравнения результатов уже выполненных исследований в аналогичном направлении с авторскими данными, которые приведены к единым значениям параметра J (1) и критерия сложности поковки ST (3). В соответствии с принятыми в анализируемых работах способами разработки технологических решений и представленными базовыми их вариантами результаты приводятся в классификации по их виду – на расчёт- ные и экспериментальные, а по способу получения – на аналогичные оптимизационным, рациональным и нерациональным решениям.

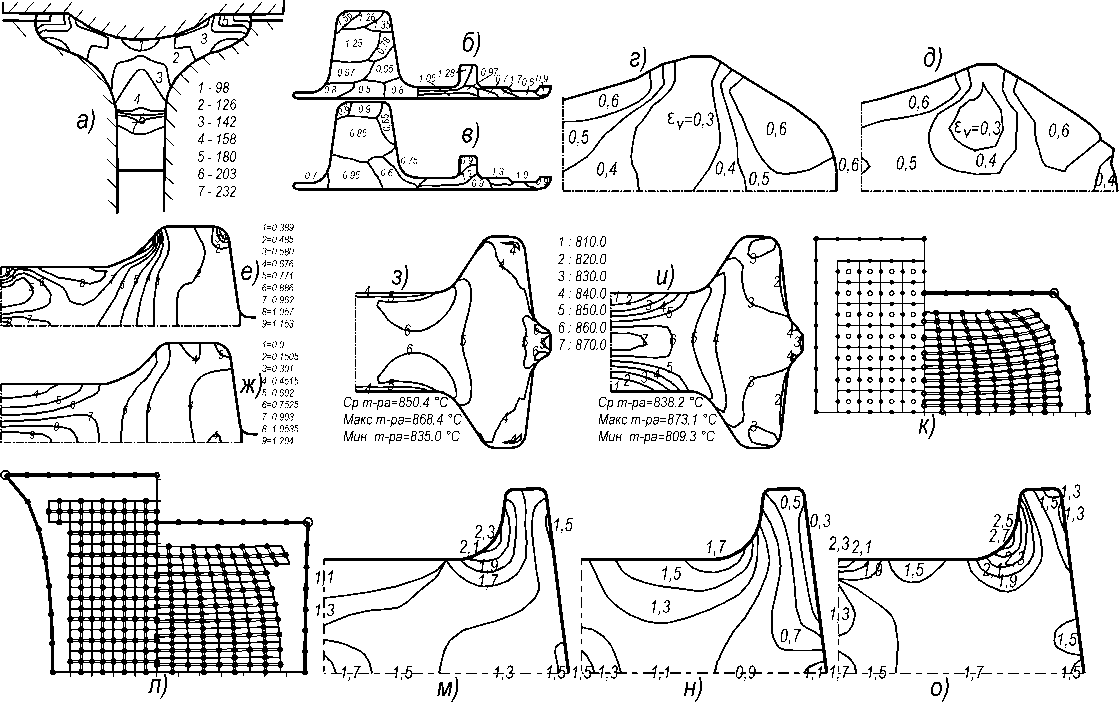
Рис. 4. Некоторые результаты, определяющие распределение полей накопленной деформации в поковках после штамповки: а – по размеру зёрен; б-ж,к-о – по накопленной деформации; з, и – по изменению температуры в процессе формоизменения (оптимальные: а, в, д, е, з, о)

Таблица 2

Анализ результатов некоторых работ по повышению равномерности деформированного состояния внутри поковок, приведенный к значению параметра J

Ссылка	Источник	Сложность поковки	Значение показателя неравномерности J
		S Т	при расчёте			в эксперименте
			Опт.	Рац.	Нерац.	Опт.	Рац.	Нерац.
Рис.4, а	[13]	1,4114	0,316	–	–	–	–	–
Рис.4, б-в	[6]	2,1805	–	–	–	0,111	0,256	–
Рис.4, г-д	[14]	0,8995	–	–	–	0,068	0,105	–
Рис.4, е-ж	[15]	1,4645	0,200	–	0,192	–	–	–
Рис.4, з-и	[16]	1,8266	0,12	0,17	–	–	–	–
Рис.4, к	[11]	0,8303	–	–	0,108/ 0,081 (0,101)	–	–	0,279
Рис.4, л	[17]	1	–	–/0,069 (0,071)	–	–	0,172	–
Рис.3	[5], [8]	2,6258	0,401/ (0,409)	0,489/0,477	0,52/0,502	0,511	–	3,041
Рис.4, м-о	[7]	1,6589	0,162/ (0,193)	0,246/0,211	0,165/0,279	0,245	0,255	0,368

Классификация по виду результатов вводится вследствие уже известного рассогласования расчётных и экспериментальных данных между собой [11], которое возможно как в результате принимаемой идеализации расчётной модели, аппроксимационного упрощения получаемых геометрических решений для экспериментального выполнения, так и в случае применения обратного моделирования в виду известной некорректности обратных задач как класса [18]. При этом в табл.2 значения J, полученные по данным численного моделирования для отдельных примеров, приводятся в нескольких вариантах, например, полученные разными методами расчёта: МКЭ/МГЭ (обратным расчётом по МГЭ).

Классификация по способу получения результатов достаточно условна, так как уже было показано (см. табл. 2), что отдельные результаты (см. рис.4, е-ж ), определённые в работах как оптимальные [15], при критериальной оценке по параметру J к таковой группе не относятся, и наоборот – базовые варианты, исходно принимаемые как нерациональные, попадают, по крайней мере, в зону рациональных значений. Первый случай отражает то, что у используемого критерия J имеется зона незначительной нечувствительности, которая относится к вариантам распределения деформаций по полям с близкой площадью, но различной конфигурацией. Второй случай, по всей видимости, относится к примерам относительного сравнения, когда базовый вариант выбран с заранее завышенными требованиями к значению J .

Таким образом, применяемые далее в настоящей работе в сравнении между собой термины «оптимальный», «рациональный» и «нерациональный» характеризуют не строгость постановки решаемой технологической задачи формоизменения при штамповке, а позволяют в общем виде оценить уровень проектного решения на стадии разработки на этапе моделирования. Так, в частности, получены уравнения моделей, по которым можно определить границы указанных диапазонов показателя J по результатам численного (МКЭ, МГЭ) моделирования формоизменения:

J^ < 0,0758 S T - 0,0982 S T + 0,1593 , (4,а)

J ™ax <  0,0545 S T + 0,0071 S T + 0,1112 , (4,б) при 2,75> S T >0,75.

С аналогичных позиций анализировались результаты и экспериментальных исследований, что обусловлено их различием с данными численного моделирования, выполненного не только МГЭ, но и МКЭ. Здесь, как и ранее, для результатов, полученных на основе оптимизационного подхода, использовалась верхняя оценка данных по соответствующей границе диапазона. Как и ранее, в экспериментальных данных имеются исключения, а оценочные модели имеют вид:

J X <  0,0532 S T + 0,0573 S T + 0,0098 , (5,а)

J m ac <  0,22 S T - 0,3812 S t + 0,3901 , (5,б) где 2,75>S T >0,75.

Предлагаемые зависимости (4) и (5) делят расчётное пространство на три области, нижняя из которых J <  J m t соответственно относится к схемам, аналогичным оптимальным, средняя J oP . <  J <  J m ac — аналогичная рациональным, а остальные значения J >  J ™ ^c _x могут быть отнесены к нерациональным вариантам схем штамповки. При этом полевое представление распределения накопленной деформации в сечении, в соответствии с применением условия (4), накладывает требования на дискретизацию параметра е i до уровня d е i <  0,3 .

При этом следует также повторно отметить и то, что не все примеры, представленные в табл.2, могут быть однозначно оценены параметром J . Так, на рис.4, е-ж представлен редкий случай, когда размеры полей в сечении поковки главным образом отличаются не площадью, а их формой. В этом случае, в отличие от первоисточника [15], автором данной статьи получены результаты противоречащие, несмотря на несущественное различие, выводам об оптимальности разработанного процесса.

Заключение. Предложен вариант приближённой диапазонной оценки поковок по показателю неравномерности распределения деформированного состояния в сечении J в зависимости от их сложности S T (2,75> S T >0,75). Приведены результаты анализа с позиций не только численного моделирования (4), но и экспериментальных исследований (5), при этом анализируются не только данные, полученные при участии автора, но и сторонние данные, приведенные автором к единому показателю неравномерности J . Классификация процессов представлена в трёхдиапазонном виде и подразделяет соответственно все технологические решения на характерные для реализации оптимизационных процедур в целевом направлении, рациональные и нерациональные.