Оценка усталостной долговечности и определение критической плоскости при многоосном циклическом нагружении с произвольным сдвигом фаз

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2019PNRPU MECHANICS BULLETIN

Опыт эксплуатации разнообразных конструкционных элементов показывает, что условия циклического нагружения и виды напряженного состояния зачастую отличаются от условий лабораторных испытаний, таких как одноосное растяжение-сжатие, изгиб или кручение. Как правило, в эксплуатации конструкционные элементы подвержены сложным (многоосным) напряженным состояниям, поэтому для оценки долговечности реальных элементов необходимо использовать многоосные усталостные критерии.

а                                        б

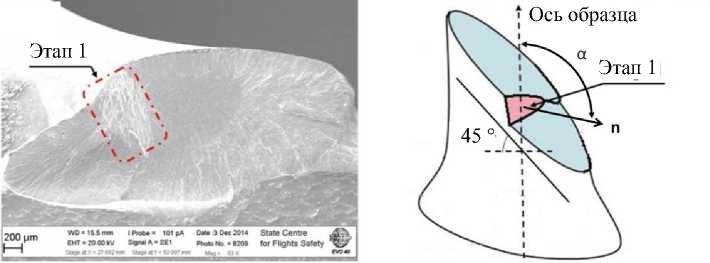
Рис. 1. Поверхность излома в титановом (ВТ3-1) образце с критической плоскостью: а – изображение, полученное с помощью сканирующего электронного микроскопа [23]; б – схематическое изображение поверхности излома с критической плоскостью

Fig. 1. The fracture surface in a titanium (BT3-1) specimen with a critical plane ( a ) an image obtained using the scanning electron microscope [23]; ( b ) a schematic image of the fracture surface with a critical plane

Для оценки усталостной долговечности элементов конструкций существуют различные модели и критерии усталостного разрушения с учетом многоосного напря- женного состояния [1–7]. Современные многоосные усталостные критерии позволяют оценить количество циклов N до разрушения образца или конструкционного элемента (усталостная долговечность) с учетом ориентации так называемой критической плоскости развития усталостных повреждений [8–17]. Такую площадку (элемент критической плоскости) можно наблюдать при фрактографическом исследовании поверхностей изломов разрушенных при циклических испытаниях образцов в зоне зарождении усталостной микротрещины (рис. 1). В данной работе предлагается процедура определения ориентации критической плоскости и, следовательно, усталостной долговечности образца, подверженного многоосному циклическому нагружению с произвольным сдвигом фаз для двух классических диапазонов усталости - малоциклового (МЦУ) и многоциклового (МНЦУ). Предлагаемая процедура основана на хорошо апробированном критерии [9, 18]. Отметим, что ранее в [22] была предпринята попытка определения ориентации критической плоскости для критерия [8], в котором при определении ее ориентации кроме размаха касательных напряжений дополнительно учитывается величина нормального к ней напряжения. В силу этого обстоятельства попытка удалась только для случая синфазного и противофазного циклического нагружения. Можно ожидать, что предложенная в настоящей работе методика позволит аналитически исследовать иные критерии, в формулировке которых с критической плоскостью связаны только касательные напряжения и не участвуют нормальные.

1.    Усталостный критерий с определением критической плоскости

Рассмотрим частицу, подверженную многоосному напряженному состоянию, которое описывается тензором напряжений σ ( t ), который зависит от времени. Выберем систему координат, связанную с главными напряжениями с , с₂, с₃. Выберем площадку, ориентированную единичной нормалью n . Для определения долговечности одноосного циклического нагружения образца вплоть до его усталостного разрушения существует соотношение Баскина [19], которое аналитически представляет усталостную кривую при различных коэффициентах асимметрии цикла (левая ветвь бимодальной усталостной кривой [20]):

с = с + с N ^в . uc

Выберем для анализа хорошо апробированный критерий многоосного усталостного разрушения, учитывающий ориентацию критической плоскости развития повреждений [9]. Этот критерий, обобщающий (как и многие другие критерии многоосного усталостного разрушения) соотношение Баскина для одноосного нагружения, выглядит следующим образом:

max T + а,с_И = A , + AN ^e, a    w h ,max    о

n где коэффициенты So, A, а, и p определяются из одноосных усталостных испытаний на растяжение-сжатие с двумя разными коэффициентами асимметрии R = 0 и R = -1 [21]; N - количество циклов до разрушения. Величина maxT есть максимальное значение размаха n сдвигового напряжения за цикл нагружения среди всех возможных плоскостей с нормальным вектором n, проходящих через рассматриваемую частицу. Выражение для величины T имеет следующий вид:

2 п

Ta2(n) = J Тa2(n, X)dX/П, 0

т a ( n ,X) = 1 max т ( п , x , t ) - min т ( п , x , t ) IL t e P              t e P          J

Величина сЯтах - эквивалентное пиковое гидростатическое напряжение в рассматриваемой частице за цикл нагружения:

^С H ,max = max ^С kk ⁽ t ^)/3- ’           t e P

Сдвиговое напряжение на заданной плоскости определяется следующим образом:

т = ( с • n ) - ( n • с • n ) n .

Выражение для размаха сдвигового напряжения, как следует из [22], можно привести к виду

^T a ^{2 (n)} = N ² = ( ^Ас 1 ^{- Ас} 2 ) 2 n ² n ^{2 +} + ( Ас 1 -Ас ₃ ) 2 n 1 ² n 2 + ( Ас ₂ -Ас ₃ ) 2 n 2 n 2 .

2.    Частные случаи напряженного состояния 2.1.    Трехосное нагружение «растяжение-сжатие»

Выберем гармонический закон изменения главных напряжений в цикле с учетом произвольного сдвига фаз. Запишем главные напряжения следующим образом:

• ^с 1 = ^с 1 m ^+с 1 a cos to t ,

^с2 =^C 2 m ^{+ с} 2 a cos ( ^to t ⁺ Ф 2 ) ,

C3 =C3m +C3a COS (tot + Ф3 ), где го - частота нагружения; ф2 и ф3 - произвольные сдвиги фаз; с1 m , с2m и с3m - средние значения, а с1 a, с2а и с3а - амплитуды компонент тензора напряжений σ(t). Размах главных компонент тензора напряжений за цикл нагружения можно записать в виде

Ас = с a ( cos to t ] - cos го t ₂) ,

Ас ₂ = с _{2 a} ( cos ( to t 1 +ф ₂ ) - cos ( to 1 ₂ +ф ₂ ) ) ,

Аст3 = G3a ( cos (tot1 + ф3 ) - cos (tot2 + ф3 )), где моменты времени tv и t2 определяются из условия максимума по времени размаха касательного напряжения на площадке с нормалью n; t1,12 е [0, T], T - 2п / to.

Кратко величину сдвигового напряжения можно записать как

Ат ² = 4 ^ A 2 sin² ( to^-ф ₁₂ ) n ^ n 2 +

2   2           22   2   2           22

+A13 sin (to^-y13)n1 n3 + A23sin (to^ — v23)nTn3 I, tkltl = ^ , A2 = ^22 + %a , 4 = An,2 + %a ,

A 23 = ^Ag 23 ^{+ А}% 3 ,

П                 %„ t2 = t1 + — = t1 + T /2 , ф12 = arctg-----, to                         Ao12

. %         . A%3

Ф 13 = arctg / ^a , Ф 23 = — arctg— -23-

^Аа 13               ^Аа 23

со следующими дополнительными обозначениями:

^А ^ 12 = ^ а ^- ^ 2 a cos Ф 2 , ^А ^ 13 = ^ 1 a ^- ^ 3 a cos Ф 3 ,

^А^ 23 = ^ 2 a cos Ф 2   ^ 3 a cos Ф 3 ,

% a = ^ 2 a ^sin Ф 2 , % a = ^ 3 a sin Ф 3 ,

^А % 23 = ^ 2 a ^sin Ф 2   ^ 3 a ^sin Ф 3 ,

A = A 2 sin 2ф,₂ n ² n I +

2        22   2        22

+ A ₃ sin 2ф,₃ n J n ₃ + A ₂₃ sin 2ф₂₃ n₂n ₃,

A - A ² cos2^₁₂ n ² n ² +

+ A ₁₃ cos2^j₃ n j n ₃ + A ₂₃ cos2^₂₃ n₂n ₃.

Моменты времени, для которых достигаются экстремальные значения размаха касательных напряжений внутри цикла при произвольном n определяются так:

T Г arctg ( as I Ac )

t ¹ = 4 [       n       + k 1 J ’

_ T Г arctg( as I Ac )

t O                          + k + 1 ,

4 ^      nJ arctg ( as / Ac )  nk tocn  ----------------- +--, k -1,2,3.

Далее, из условия экстремума функции Ат²( x i ), i = 1,2,3, при ограничении ^ x_k -1 для моментов времени к и t ₂ определяются компоненты вектора нормали x i - n ², 0 <  x i <  1:

x1 - (2b1b2 - b2b12 ) / (4b1 b2 - b122 ), x2 - (2b1 b2 -b1 b12)/(4b1 b2 -bn), X3 - 1-X1 -x2, b1 - A23 sin2 ( to^0 - Ф13 ), b2 - A223 sin2 ( to^0 - Ф23 ),

• ^b12 ^- A 1²3 ^{sin 2} ( ^to^ 0 ^-V 13 ) ⁺

• ⁺ A 223 ^sin 2 ( ^to^ 0 ^-Ф 23 ) ^- A 122 ^sin 2 ( ^to^ 0 ^-Ф 12 ) .

Отбор компонент x , соответствующих максимальным и минимальным значениям размаха касательных напряжений, проводился явным образом, так как отделить их путем исследования квадратичной формы вторых производных в данном случае не удается, в отличие от случая синфазного и антифазного нагружения [22]. Если функция Ат²( x ) не имеет максимума внутри области 0 <  x i <  1, то с помощью упрощенного анализа определяются значения компонент x , соответствующие экстремумам Ат²( x ) на границах этой области:

x1 - 0, x2 -x3 - 0,5, либо x2 - 0, x1 -x3 - 0,5, либо x3 - 0, x1 - x2 - 0,5.

После вычисления функции Ат²( x _z-) при найденных значениях x выбирается тот случай из найденных экстремумов, где эта функция имеет максимальное значение.

Аналогичным образом получается выражение для определения момента времени, когда эквивалентное гидростатическое напряжение а„стя ^ максимально.

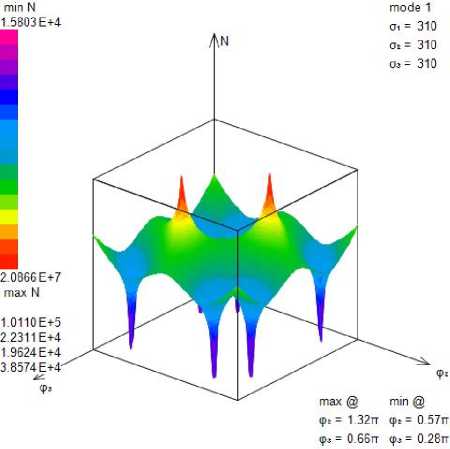
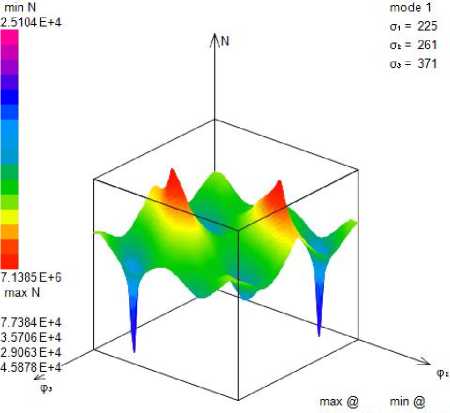
С учетом полученных значений t_v, t₂ и компонент нормали x _;- - n 2 из критерия многоосного усталостного разрушения можно определить количество циклов N для произвольных величин амплитуд напряжений при циклическом нагружении в зависимости от сдвига фаз. Проведенные расчеты показывают значительное влияние сдвига фаз на усталостную долговечность, что видно на рис. 2, где показана зависимость N ( ф ₂ , ф ₃ ) для конкретных значений амплитуд главных напряжений. Так, например, на рис. 2, а приведены результаты для гидростатического напряженного состояния, которое без сдвига фаз вообще не должно приводить к усталостному разрушению в связи с отсутствием касательных напряжений на любой площадке.

а

Рис. 2. Усталостная долговечность, представленная в виде количества циклов N , как функция от сдвигов фаз ф₂ и ф₃

Фе = 0.47тт фг = 1.64тт

Ф» = 1 _24тт ф» = 0.22п

б

Fig. 2. Fatigue life in terms of N cycles as a function of shifts of phases ф₂ , ф₃

• 2.2. Двухосное нагружение вида «кручение с изгибом»

Аналогичный анализ был проведен для широко распространенного вида нагружения – кручения с изгибом. При этом также учитывается произвольный сдвиг фаз. В данном случае в циклическом процессе нагружения отличны от нуля компоненты напряжений a₃₃ ( t ) и т₂₃ ( t ) , которые меняются по гармоническому закону:

^т 23 ( t ) = ^т m ^+т a cos ^{to t 1}

^a 33 ( t )   ^a m ■ ^a a cos ( to t ⁺ ф ) ¹

где го - частота нагружения; ф - произвольный сдвиг фаз; a _m и т _m - средние значения, а ст _a и т _a - амплитуды компонент тензора напряжений σ ( t ). Размах главных компонент тензора напряжений за цикл нагружения можно записать в виде

Ат ₂₃ = т _a (cos to t 1 - cos to t ₂ ) =

„    . f A - t I | A + t

= 2т„ sin to —---1 sin to — a (    2 J (

Aa ₃₃ = ст _a ( cos(to t 1 + ф) - cos(to t ₂ + ф) ) =

„     . f A - t I . f A + t

= 2afl sin I to —---1 I sin I to — где моменты времени t и t определяются из условия максимума по времени размаха касательного напряжения на площадке с нормалью n; t1,12 е [0, T], T = 2п / to.

Кратко величину сдвигового напряжения можно записать как

Ат ² = 4sin ² to—— t— Гт 2 X sin ² to^ + ।_ a т

+ т _a a _a X _a sin to^sin ( to^ ) + a _a ² X _a sin ² ( to^ + ф

• ^{t— + tl}- = ^ , ^X т = ^x 2 ⁺ x 3 ^{- 4 x} 2 x 3 ,

X ат = ² V x 2 x 3 ^{( 1 - 2 X} 3 ) , X a = ^X 3 ^{( 1 - X} 3 ) со следующими дополнительными обозначениями:

B S = ^т a ^a a^X ат ^sin ф^{+ a2 X} a ^sin2 Ф ^,

B e = т ^ Х т +т a a a^X ат Cos ф + а ^ Х a COs2ф.

Были определены моменты времени, для которых достигаются экстремальные значения размаха касательных напряжений внутри цикла при произвольном n :

T f arctg ( bs I Be)

• t ¹ = 4 [        П       ⁺ k -—J ¹

_ T ( arctg (bs / Be)

• t o                            + k + 1 ,

• 41       n

arctg ( b s I B e ) n k

(oE =--- 1-- , k = 1,2,3.

Из условия экстремума функции Ат²( x, ), i = 1,2,3, при ограничении ^ х_к = 1 были определены соответствующие данным моментам времени t ₁ и t ₂ – компоненты вектора нормали x_i :

x 3 =

^T a sin² ю^ 0 + . 2 sin² ( ю^ 0 + ф ) 2 ^ 2 sin² (^ о +ф )

x 2 = 0 , x 1 = 1 - x 2 - x 3 .

Отбор компонент x , соответствующих максимальным и минимальным значениям размаха касательных напряжений, также проводился явным образом. Если функция At2(x) не имеет максимума внутри области 0 < xi < 1, то с помощью упрощенного анализа были определены значения компонент x , соответствующие экстремумам At2(xi) на границах этой области.

Аналогичным образом было получено выражение для определения момента времени, когда эквивалентное гидростатическое напряжение а„стя ^ максимально.

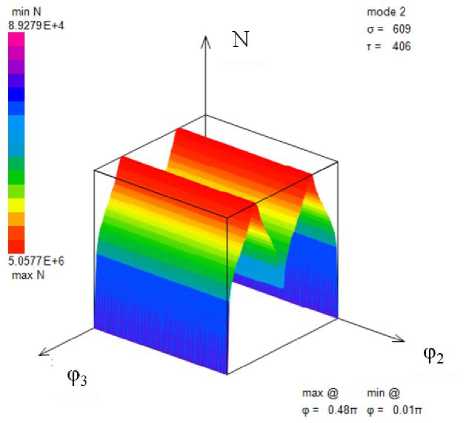
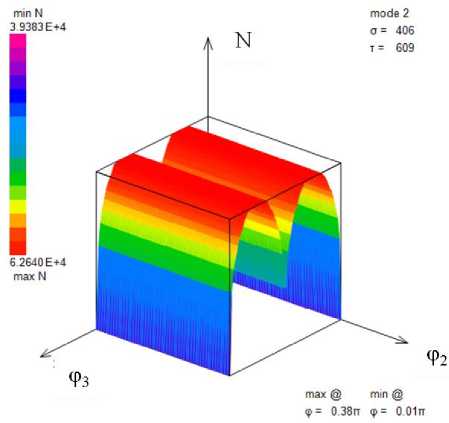
Как и в предыдущем случае нагружения, в данном варианте можно определить количество циклов N для произвольных величин амплитуд напряжений многоосного циклического нагружения в зависимости от сдвига фаз. Проведенные расчеты показывают значительное влияние сдвига фаз на усталостную долговечность, что видно на рис. 3.

а

Рис. 3. Усталостная долговечность, представленная в виде количества циклов N , как функция от сдвига фазы ф = ф₃

б

Fig. 3. Fatigue life in terms of cycles N as a function of a shift of phase ф = ф₃

3.    Сравнение рассматриваемого критерия с экспериментальными данными

Для оценки корректности определения ориентации критической плоскости было проведено сравнение с немногочисленными экспериментальными результатами, с учетом сдвига фаз для углеродистой стали 0,51 % при усталостных испытаниях на изгиб с кручением [24], а также с другим известным многоосным критерием усталостного разрушения [11]. Приведем сравнительную таблицу для нагружения вида «изгиб с кручением». Первые два столбца представляют собой амплитуды изгибающих и крутильных напряжений. Третий столбец – сдвиг фаз между ними. В четвертом по седьмой приведены данные для угла ориентации, который является углом между продольной осью образца и нормалью к критической плоскости (см. рис. 1). Численные результаты были получены путем прямого перебора для рассматриваемого критерия [9], а именно, с малым шагом были рассчитаны возможные комбинации дискретных значений времени и сдвига фаз. Ориентация плоскости с наибольшим найденным значением размаха касательного напряжения была выбрана в качестве критической; аналитические значения для угла α получены с применением формул, приведенных выше. Предлагаемая аналитическая процедура приводит к результату в 200 раз быстрее, чем прямой числовой перебор.

Из приведенной таблицы видно, что аналитическая процедура дает результаты, полностью совпадающие с трудоемким численным определением ориентации критической плоскости для выбранного критерия усталостного разрушения Пападопулоса [9, 18] и относительно близкие к экспериментальным и полученным на основе иного критерия усталостного разрушения с определением критической плоскости [11].

Экспериментальные и расчетные данные

Experimental and calculated data

σ , MPa	τ , MPa	δ	α ( ⋅π ) экспер. [24]	α ( ⋅π ) Carpinteri [11]	α ( ⋅π ) численно [9]	α ( ⋅π ) аналит.
0,00	201,11	0	0,249	0,250	0,250	0,250
162,85	195,69	0	0,194	0,193	0,193	0,193
274,68	137,34	0	0,128	0,125	0,125	0,125
141,95	171,18	π/6	0,177	0,197	0,193	0,193
255,06	127,53	π/6	0,090	0,119	0,125	0,125
147,15	177,56	π/6	0,120	0,206	0,213	0,213
255,06	127,53	π/6	0,045	0,094	0,125	0,125
152,45	184,23	π/6	0,158	0,207	0,000	0,000
264,87	132,44	π/6	0,000	0,076	0,000	0,000
308,03	63,86	π/6	0,000	0,055	0,000	0,000

4.    Численный подход

Рассмотрена задача усталостного разрушения диска компрессора газотурбинного двигателя в полетных циклах нагружения. Аналитическим и численным методам расчета напряженно-деформированного состояния дисков и лопаток ГТД на различные воздействия посвящена обширная литература [25–31]. Для примера был рассмотрен диск переменной толщины (модельный вариант диска компрессора газотурбинного двигателя) под воздействием центробежных нагрузок. Напряженное состояние диска рассчитывалось численноаналитическим методом [30–31], обобщающим на неосесимметричный случай метод, разработанный в [26].

h/Га 0,8

0,6

0,4

0,2

• 1      2      3      4      5      6      7      8 ^r/“

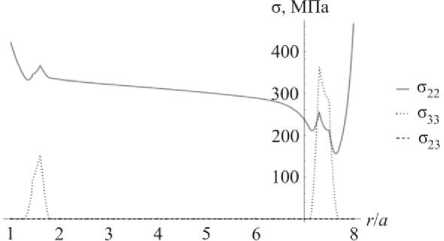
  Геометрия половины поперечного сечения диска представлена на рис. 4, а , распределение по радиальной координате некоторых компонент тензора напряжений – на рис. 4, б . Значения параметров частоты вращения ω= = 600 1/c, модулей упругости и плотности λ= 78 МПа, µ=44 МПа, ρ =4370 кг/м³ (титановый сплав ВТ3-1). Для данного диска была проведена оценка количества циклов N до разрушения с выбранным пределом усталости для реверсного цикла 350 МПа. Было получено несколько схожих результатов для разных частей диска, все они лежат в диапазоне от 12 ⋅ 10³ до 40 ⋅ 10³ циклов, что соответствует экспериментальным данным [30].

б

Рис. 4. Распределение напряжений в диске рассматриваемой геометрии без учета v-образных углублений

Fig. 4. Stress distribution in a simplified disc of the considered geometry without v-shaped notches for blades

Также был рассмотрен более реалистичный элемент конструкции – сегмент диска компрессора низкого давления газотурбинного двигателя с лопаткой, представленные на рис. 5, a . Лопатки подвержены аэродинамическим нагрузкам, лопатки и диск подвержены центробежным нагрузкам. Рассматриваются следующие типы контактных условий на границе диска и лопаток – полное сцепление и проскальзывание с трением с возможностью отлипания. Расчеты показали, что наиболее опасными с точки зрения зарождения усталостных трещин являются окрестности зон контакта диска и лопаток, имеющих вид соединения типа «ласточкин хвост».

Также показано, что наилучшее соответствие расчетных и экспериментально наблюдаемых зон концентрации напряжений достигается при учете возможности отлипания и проскальзывания контактных границ диска и лопаток.

Концентрация напряжений в окрестности соединения «ласточкин хвост» приводит к необходимости значительного сгущения расчетной сетки в этой области. Оценки показывают, что расчет полномасштабной модели диска с полным набором лопаток и с достаточной степенью сгущения, а также с учетом значительного времени обработки каждого контактного условия неэкономичен по времени. В то же время при рассмотре- нии сектора диска с единственной лопаткой остаются неизвестными граничные условия на его боковых поверхностях, так как в силу разворота лопаток относительно оси вращения и самого вращения задача не является осесимметричной. Поэтому расчет проводился в два этапа. Сначала была создана сетка с умеренным сгущением для полной модели. Количество элементов ~2 ⋅105 . В дальнейшем для задачи на секторе диска с сильным сгущением сетки в качестве условий на боковых поверхностях использовались перемещения, полученные из расчета на полной модели. Сетка значительно сгущена в окрестности ожидаемых концентраторов напряжений. Общее количество элементов не превосходит 100 000, что вполне приемлемо для проведения расчетов на персональном компьютере.

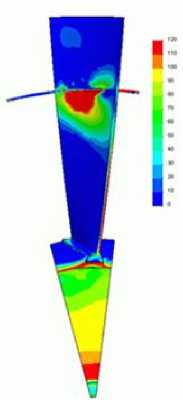
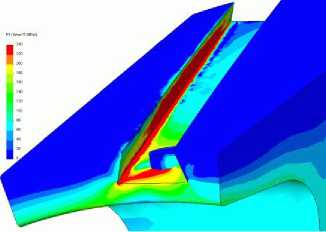
По результатам конечно-элементного расчета на рис. 5, б показано распределение напряжений в зоне контакта диска и лопатки. На рис. 5, в показано количество циклов N до разрушения в наиболее нагруженной области диска – в углу паза для закрепления лопатки для трех критериев (слева направо): классических критериев [6] и [7], сформулированных для инвариантов тензора напряжений и не использующих понятие критической плоскости, и для критерия [9], учитывающего ориентацию критической плоскости. Критерии [6] и [9] дали оценку долговечности дисков ГТД на уровне 35 000–50 000 циклов. Критерий [7] предсказал возможность усталостного разрушения в 20 000 полетных циклов. В целом все эти критерии дали сходное расположение зон усталостного разрушения.

б

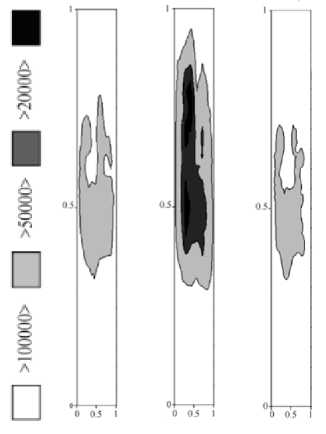
Рис. 5. Оценка долговечности диска компрессора; а – сегмент диска компрессора и лопатка; б – напряженное состояние в зоне контакта диска и лопатки; в – количество циклов N до разрушения в наиболее нагруженной области диска для критериев [6, 7, 9]

Fig. 5. Fatigue life assessment of the disc; ( a ) is a segment of a compressor disc and a blade, ( b ) is the stress state within the contact zone between the disc and the blade, ( c ) is the amount of cycles N to breakdown within the most vulnerable zone of the disc for criteria [6, 7, 9]

Заключение

Предложена процедура аналитического вычисления ориентации критической плоскости для многоосного циклического нагружения при произвольном сдвиге фаз в случаях классических усталостных диапазонов – малоцикловой и многоцикловой усталости. Проведено сравнение исследуемого критерия с экспериментальными данными и численными расчетами, произведенными с использованием иного критерия.

Рассмотрен диск компрессора газотурбинного двигателя, подверженный полетным циклам нагружения. Путем распределения напряжений, рассчитанного приближенным численно-аналитическим методом, а также распределения напряжений, рассчитанного методом конечных элементов, определены зоны наи- большей концентрации напряжений, ориентация критической плоскости в зонах концентрации и получены оценки долговечности (число циклов до разрушения N ~ 35 000 – 50 000) эксплуатации диска с использованием выбранного многоосного критерия усталостного разрушения.

Работа выполнена при поддержке Российского научного фонда, проект РНФ № 19-19-00705.

Acknowledgment

The work was supported by The Russian Science Foundation, Project RSF No. 19-19-00705.