Оценка устойчивости бортов карьеров в скальных грунтах

1.    INTRODUCTION optimisation of mining sequence of blocks

Strategic mine planning is a key to the success of mining projects and its critical task is to determine an optimal and practical mining schedule over the life of mine, or long-term production scheduling. The aim is to maximise the economic outcome of exploiting a mineralised deposit, commonly calculated in the form of Net Present Value (NPV), subject to a range of constraints, such as land lease boundary, capacity of mining equipment fleet, processing plant, blending grade and slope safety [6].

The fundamental input of mine planning process is a resource model of the deposit in three-dimensional (3D) space consisting of arrays of unit blocks, of which each block contains necessary information for mine planning procedure, such as metal grade, density and lithology. The resource block model is then converted into an economic block model by using commodity prices, operational costs and recovery rates. From this perspective, the production scheduling problem of an open pit mine is the bounded by these aforementioned constraints and the objective is to maximise economic profit of mining project. Naturally, this is an application area of operation research (OR).

The pioneering work of applying OR in open pit mine planning was credited for [3] using a linear programming (LP) model. In this LP model, linear variables are introduced to each block to represent the proportion of material being scheduled in each mining period. Despite its robustness, the major shortfall is that underlying blocks can be scheduled while the blocks above have not yet been completely removed and this is impractical. For this reason, integer variables are introduced to maintain the integrity of mining blocks, i.e. blocks are scheduled as a whole as illustrated in Figure 1. In this case, integer variables are used in a special type of binary with only two possible outcomes of either 0 or 1, where 1 if block is removed, 0 otherwise.

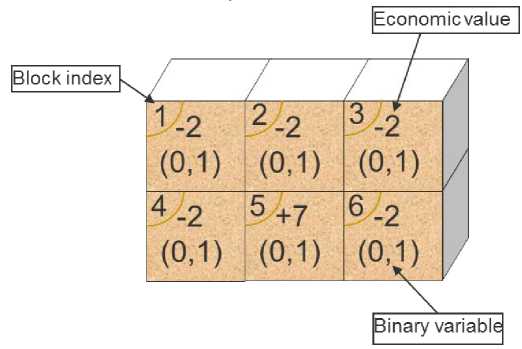
Fig. 1. Demonstration of a hypothetical 2D deposit with block index, block economic value and binary variable

In Figure 1, let us assume a hypothetical two-dimensional (2D) block model constituted by six blocks, of which only block 5 is ore with a positive economic value of +7, the rest is waste with negative economic value of -2. Let us also assume the mine plan consists of one period and the only operational constraint is slope safety of 450. In this simplistic case study, one can see the optimal production schedule is ore block 5 being mined with three overburden blocks 1, 2, and 3 so the maximum mining profit is +1. Therefore, if an IP model is constructed to optimise this hypothetical mine planning problem, its task is to return output of binary variables correctly, i.e. those of blocks 1, 2, 3, and 5 are 1, meanwhile those of blocks 4 and 6 is 0, as shown in Figure 2.

This type of OR technique is referred to as integer programming (IP) and its expansions are mixed integer programming (MIP), mixed integer linear programming (MILP) and stochastic integer programming (SIP). References of methodology and applications of these techniques can be found at the works of [1, 7, 8]. For a scheduling problem of a block model including n blocks and the life of mine is p periods (years), the scale of the mathematical model is determined by the number of binary variables n⋅ p. In real mining projects, this number could easily reach a magnitude of millions and such a large scale mathematical could not be solved using the current computer technology.

To deal with the challenge of applying OR in open pit mine planning, we deployed our inhouse block aggregation technique called TopCone Algorithm (TCA) in this paper. TCA combines blocks into TopCones (TCs) in specific conditions so that it has the following features:

• 1.    The mining of each TCs following certain sequence does not violate slope safety.

• 2.    The combination of all TCs forms an ultimate pit limit.

• 3.    The number of TCs can be controlled by adjusting input conditions.

The performance of TCA is demonstrated in a hypothetical 2D deposit, shown in Figure 3. By applying a condition that requires a minimum of two blocks per TC, four TCs were generated from a block model of 21 blocks. Note that the number of TCs generated can be reduced if the required number of blocks per TC increases.

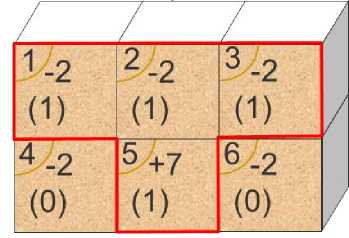
Fig. 2. Result of solving production scheduling problem using binary variables

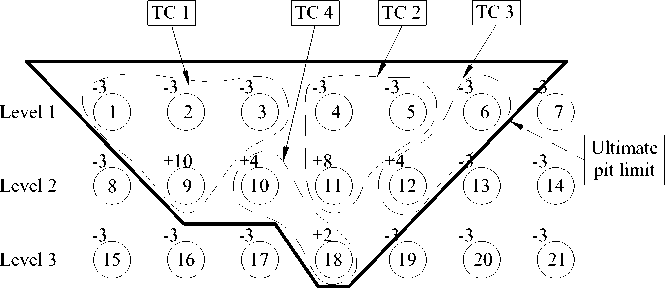
Fig.3. Demonstration of TCA on a hypothetical 2D case study with minimum two blocks per TC Index inside circle is block ID, outside is block economic value

Next in the paper, we introduce the methodology of IP and a proposed mine planning framework using IP and TCA. It is then followed by a case study in the Sin Quyen copper deposit and conclusions.

2.    METHODOLOGY

The problem of open pit production scheduling using IP can be described as follows:

Let us define X_i ^t is the binary variable to determine whether block i is scheduled in period t ( X_i ^t = 1) or not ( X_i ^t = 0). Where d is the discount rate of dollar value and V is the economic value of block i in the unit of dollar, the objective function of the IP model is to maximise NPV and can be expressed as:

max ЕЕ.  1 v V • Xt t i (1 + d)1

Denote T as the tonnage of block i and MC , MC respectively are maximum and max minimum mining capacities, the constraints for mining capacities of the IP model can be expressed as follows:

Upper bound: ЕTt • Xt < MCmax

Lower bound: ЕT, • X‘ > MCmin

i

A full set of constraints can be found in the references provided in the introduction section. As discussed in the previous section, in this study we deployed TCA to aggregate blocks into TCs to reduce the scale of the mine planning model.

The new open pit mine planning framework and its three phases can be illustrated in Figure 4.

Phase 1: Ore resource estimation. During this phase, a block model is constructed using tools like Surpac, DataMine or Vulcan. The metal grade and tonnage of unit blocks can be assigned using estimation techniques like inverse distance or kriging. More details of modelling a deposit can be found in the work of [4, 5].

Phase 2: Block aggregation. TCA is implemented on the resource block model to cluster blocks into TCs to significantly reduce the scale of data to facilitate the performance of the downstream IP-based production scheduling model.

Phase 3: Strategic mine planning. In this phase, an optimal long-term production scheduling is obtained by solving the IP model using CPLEX [7]. As data has been compressed before formulating and solving the IP model, the solution time to achieve an optimal solution is relatively quick.

3.    APPLICATION AT SIN QUYEN COPPER DEPOSIT, VIETNAM

Sin Quyen is the largest copper deposit in Vietnam. Located in the Northern West, the deposit lies 130 km along the right bank of Hong River and the border of Vietnam – China. Currently, a mining project of the deposit is under the management of Vietnam National CoalMineral Industries Holding Corporation (Vinacomin). The location of Sin Quyen copper mine is depicted in Figure 5.

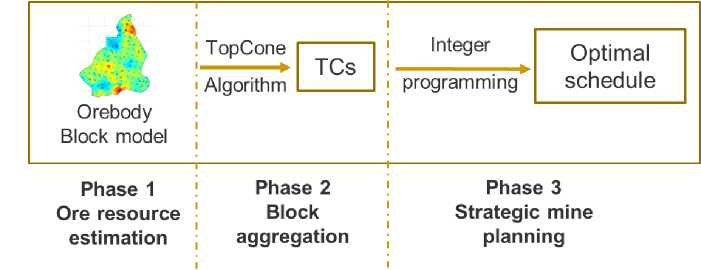
Fig. 4. Systematic illustration of the proposed mine planning framework

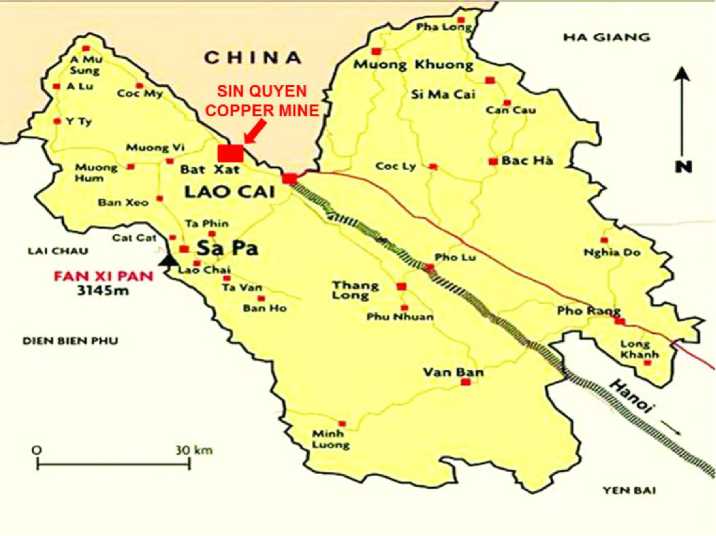
Fig. 5. Location map of Sin Quyen copper mine

The block model of the deposit was created using Surpac. The block size is 25x25x25 m, amongst the total of 802,944 blocks, 10,613 blocks are ore. Ordinary Kriging was used to estimate copper grade of the block model, meanwhile inverse distance with distance power of 0 was used to estimate specific gravity of ore and waste blocks separately. The ore resource model was then converted into an economic block model using a hypothetical set of economic parameters, i.e. copper metal price, mining and processing cost and recovery rate.

TCA was implemented on the block model and 492 TCs were generated from 802,944 blocks. Clearly, the scale of data has been significantly reduced. The map of all TCs and the ultimate pit constituted by combining all TCs is presented in Figure 6.

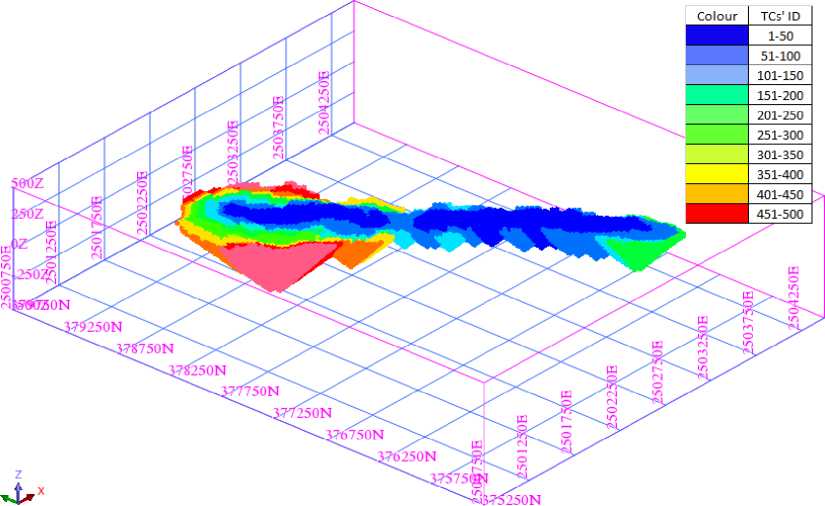
Fig. 6. 492 TopCones and the ultimate pit limit looking North-East

In the next step, all 492 TCs were fed into an IP model and solved by CPLEX. For comparison purpose, a mine plan was also constructed using Whittle software, one of the most common commercial mine planning software package used in mining industry. The production schedule results of two approaches are presented in Figure 7. Note that the scheduling parameters used in this case study is hypothetical to demonstrate the performance of the proposed model only. The model, however, can be quickly adapted to take correct input parameters.

From Figure 7, Whittle’s schedule showed a lack of ore tonnage in the first period and a stronger variation of total mining capacity. On the other hand, the proposed mine planning model yielded a better scheduling scenario with a considerably higher NPV of 18.86 %.

To demonstrate the practical mining sequence of the TCA-based IP model, its plan view and typical cross-sections are presented in Figure 8.

Production Scheduling Comparison

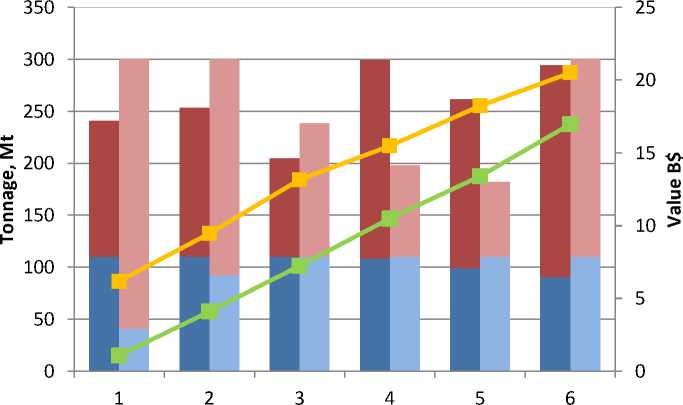
Period waste tonnage - TCA-based IP    ^™ waste tonnage - Whittle

^™ ore tonnage - TCA-based IP      ^™ ore tonnage - Whittle

—■— NPV - TCA-based IP              -■- NPV - Whittle

Fig. 7. Comparison of production schedules suggested by the proposed mine planning model using TCA-based IP and Whittle

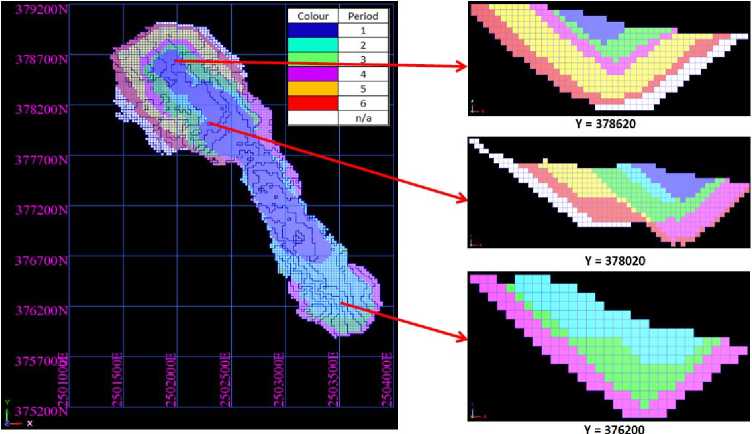
Fig. 8. Plan view and typical cross-sections of the proposed mine plan

4.    CONCLUSIONS AND SUGGESTIONS

In this paper, we outlined the significant advantages of the application of operations research in open pit mine planning. The mathematical models proved their superiority in handling complicated mine planning and production scheduling problems where a large amount of data needs to be processed under various conditions. The fundamental obstacle of this approach is the intense number of binary variables has been solved efficiently by combining blocks into TopCones using TopCone Algorithm.

The application of the proposed model on the Sin Quyen copper deposit demonstrated its superiority over a popular commercial mine planning software package with a significant NPV improvement. This also proved a high potential of applying the proposed mine planning model in the industry.

In the future, more works need to be done aiming at commercialising the mine planning model, such as developing a user-friendly interface and a stand-alone 3D visualisation.

branch and cut to open pit mine scheduling. Journal of global optimization, 27(2-3), 349-365.