Оценка вероятности безотказной работы элементов конструкций с трещиноподобными дефектами

Отказы элементов конструкций возникают как результат несовершенства или нарушения правил проектирования (конструкторские отказы), процесса изготовления (производственные отказы) или условий эксплуатации (эксплуатационные отказы). Трещины инициируются на дефектах различного рода в зоне действия наибольших напряжений.

Дефекты (несовершенства) по размеру могут быть допустимыми или недопустимыми. При наличии недопустимых дефектов детали выбраковываются. В большинстве же эксплуатируемых элементов конструкций имеются допустимые дефекты, возникающие в процессах производства металлов и сплавов, литья, ковки, сварки, механической обработки и т. д. Некоторые из этих дефектов являются трещиноподобными и могут рассматриваться как элементы начала разрушения, то есть как первоначальные трещины, пусть даже достаточно малого размера.

При однократном приложении постоянно возрастающей нагрузки разрушение материалов

в зависимости от степени пластической деформации может быть хрупким, квазихрупким и вязким (пластическим). Хрупкое разрушение происходит в результате распространения магистральной трещины после макроскопически незначительной пластиче ской деформации, сосредоточенной в приповерхностной зоне трещины. При квазихрупком разрушении существуют пластическая зона перед фронтом трещины и пластически деформированный материал у поверхности трещины. Остальной, значительно больший по величине объем тела находится в упругом состоянии. Вязкое разрушение происходит после существенной пластической деформации, протекающей по всему или почти по всему объему тела. Иногда выделяют еще и квазивязкое разрушение, занимающее промежуточное положение между вязким и квазихрупким.

Основополагающей является работа А. Гриффитса [6], где предложен энергетический подход для случая хрупкого разрушения при наличии трещины. Экспериментальные и теоретические исследования Дж. Ирвина [7] привели к силовому подходу и концепции квазихрупкого разрушения. Условием локального разрушения тела (страгива-ния трещины) по Ирвину является равенство коэффициента интенсивности напряжений К, его критическому значению Kic :

K i =K ic . (1)

Критический коэффициент интенсивности напряжений (иногда его называют вязкостью разрушения) является константой материала и подлежит экспериментальному определению. Коэффициент интенсивности напряжений определяется по формуле:

K i = Y i (l) а 4П , (2)

где Y I (l) - функция, зависимая от геометрической формы детали и длины трещины; а - действующее номинальное напряжение; l - длина (полудлина) трещины.

Для определения функции Y i (l) в элементах конструкций сплошной формы существует множество методов. Мы не будем на них останавливаться, поскольку вид функции Y i (l) для очень многих частных случаев приведен в литературе [2], [3], [7], [8]. Заметим лишь, что для бесконечной пластины со сквозной трещиной длиной 2 1 Y_I(l) = 1.0, а для полубесконечной пластины с граничной краевой трещиной длиной l Y_I(l) = 1.1215.

Пусть воздействующее на элемент конструкции напряжение является стационарным случайным процессом a (t) . Основными характеристиками такого процесса являются спектральная плотность S „ ( ю ) и математическое ожидание а . При наличии трещиноподобного дефекта длиной (полудлиной) l с использованием зависимости (2) получаем:

K i (t) = Y i (l) ^ a (t) . (3)

Очевидно, что спектральная плотность случайного процесса коэффициента интенсивности напряжений определится по формуле:

Воспользовавшись положениями теории выбросов случайных процессов [5], запишем для среднего числа пересечений процессом K (t) уровня K _c в единицу времени

to

P k IC = J f(K IC, и ) и d и .              (6)

Величина P_{K ic} называется временной плотно -стью вероятности. Среднее число пересечений уровня K_IC за время т определится по формуле:

N + (t ) = т P k _k .                 (7)

Для гауссовского стационарного случайного процесса

N + (t ) = т — exp 2π

f (Kic — Ki) 2)

_ 2D К ,

где К - математическое ожидание случайного процесса

K(t) , К i (t) = Y(l)4П а ;

D_K - дисперсия случайного процесса K i (t) :

D k = J S k ( ю )d ю ;

ю _e - эффективная частота процесса К i (t) , с^-1:

ю e

to

J ю2 Sk( ю )d ю

D k

1 / 2

Полученные зависимости (3)–(9) дают возможность оценить вероятность безотказной работы. При этом используем допущение, предложенное В. В. Болотиным [1] для вероятности отказа Q(t) : Q(t) « N + (t) .

Очевидно, вероятность безотказной работы определится:

P(t) « 1 - N + (t) .

S k ( ю ) = Y i (l)^"lS _а ( ю ) .           (4)

Предполагаем, что случайный процесс K i (t) является стационарным и дифференцируемым. Обозначим

Для гауссовского стационарного случайного процесса, учитывая (8), соответственно:

_U (t)=dK K t) .

dt

p(t) ~ 1- t Te exP

2π

f (K ic - K i ) 2 )

( 2D к J

Нас интересует вероятность того, что случайная функция K (t) выйдет за пределы K c , то есть произойдет выброс за указанный уровень.

Для оценки вероятности безотказной работы весьма интересен подход А. А. Свешникова [4], основанный на использовании распределения Пуассона. Исходя из предположения о том, что распределение отказов следует закону Пуассона,

Оценка вероятности безотказной работы элементов конструкций с трещиноподобными дефектами

получено, что вероятность наступления m событий за время наблюдения 0 < т <  t составляет:

;m

Pm = —e ^х , ( m = 0,1...). m!

Здесь λ – математическое ожидание числа отказов.

Вероятность безотказной работы будет определяться как вероятность того, что за время t не произойдет ни одного отказа (выброса K , (t) за уровень K ic ), то есть P, . Таким образом, подход А. А. Свешникова дает оценку:

P(t) « exp [ - N + (t) ] .               (12)

Для гауссовского стационарного процесса нагружения с учетом зависимостей (8) и (12) имеем:

P(t) = exp

, to e

— t — exp 2π

(K ic - K i ) 2 2D k

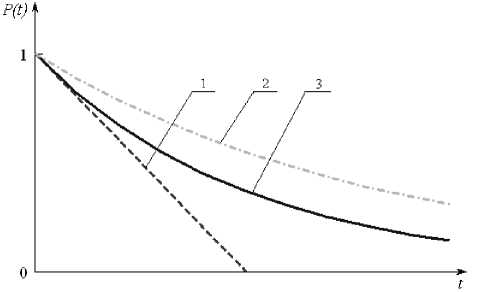
Графики зависимости вероятности безотказной работы от времени:

1 – подход В. В. Болотина; 2 – подход А. А. Свешникова;

3 – действительная зависимость

На рисунке приведены графические зависимости вероятности безотказной работы. Кривые 1 и 2 соответствуют подходам В. В. Болотина и А. А. Свешникова, кривая 3 – реальная зависимость.