Оценка вероятности безотказной работы системы ROPS лесозаготовительных машин c позиций механики разрушения

Для лесной техники, работающей в условиях сильнопересеченной местности, характерны такие аварийные ситуации, как опрокидывание машин или падение на них тяжелых предметов. Действующие нормативно-технические документы, регламентирующие требования к безопасности операторов лесных машин, предписывают оснащать кабины устройствами защиты при опрокидывании (ROPS – Roll-over protective structures) для снижения риска травмирования в случае возникновения аварийной ситуации. Так, стандартом ИСО 8082 допускается проведение статических лабораторных испытаний ROPS при боковом, вертикальном и продольном нагружении, при этом одним из главных требований является неразрушение конструкции ROPS при испытаниях.

Методам оценки показателей безотказности с позиций механики разрушения посвящены работы В. В. Болотина [1], А. В. Питухина [3], [4] и ряда других авторов. В работе [4] отмечается, что материалы реальных конструкций еще до начала эксплуатации имеют несовершенства в виде несплошностей, инородных неметаллических включений, раковин, газовых пор, дефектов сварки и механической обработки. Трещины могут развиваться в зонах действия наибольших механических напряжений, инициируясь на дефектах различного рода, которые можно рассматривать

как элементы начала разрушения (первоначальные трещины малого размера). В то же время одним из важнейших показателей безотказности является вероятность безотказной работы R , при решении задач оптимизации он зачастую входит в целевую функцию [8], [9], [10], поэтому представляется целесообразной разработка метода оценки вероятности безотказной работы конструкции ROPS в зависимости от длины и вида трещины.

В механике разрушения в зависимости от степени пластической деформации различают хрупкий, квазихрупкий и вязкий механизмы разрушения в условиях однократного воздействия постоянно возрастающей нагрузки. В работе А. Гриффитса представлен энергетический подход для описания механизма хрупкого разрушения при наличии трещины. Последующие исследования Дж. Ирвина привели к созданию концепции квазихрупкого разрушения и силового подхода, получившего наиболее широкое распространение в инженерных приложениях и связанного с использованием такого критерия, как коэффициент интенсивности напряжений K_I . Согласно Дж. Ирвину, трещина начнет распространяться, если значение коэффициента интенсивности напряжений K I достигнет критического значения K_IС :

K I = K IС .

Критический коэффициент интенсивности напряжений K_IС считается постоянной величиной для данного материала, его значения приведены в литературе [5] для различных материалов.

Коэффициент интенсивности напряжений определяется по формуле

K i - Y , ( l ) - a- X- ,               (1)

где Y I (l) – коэффициент, учитывающий длину трещины и геометрическую форму детали; σ – нормальное напряжение, растягивающее трещину; l – длина (полудлина) трещины.

ОЦЕНКА ВЕРОЯТНОСТИ БЕЗОТКАЗНОЙ РАБОТЫ

Оценим вероятность безотказной работы в предположении, что плотность распределения вязкости разрушения материала элемента ROPS f₁(K_IC) и коэффициента интенсивности напряжений f 2 (K I ) известны и статистически независимы. В данном случае вероятность безотказной работы можно выразить как вероятность того, что коэффициент интенсивности напряжений K I не превысит вязкости разрушения K IС

R - Pr {Kic > Ki } = Pr {Ke - Ki > 0} .

Вероятность того, что коэффициент интенсивности напряжений находится в интервале f K 0 - K; K 0 + K )

( I 2 I 2 J

Pr ^f K 0 - ^K <  K, <  K 0 + dK I -) - f t K, ¹) dK,

I 2 II 2 2 II .

Вероятность того, что вязкость разрушения K_IС превысит некоторое значение коэффициента интенсивности напряжений K_I ⁰

те

Pr { K_K >  K , } - J f. ( K_K ) dK ic .

K I ⁰

Вероятность того, что значение коэффициента интенсивности напряжений KI заключено в малом интервале dKI, а вязкость разрушения KIС превышает коэффициент интенсивности напряжений, задаваемый этим интервалом, имеет вид те f2 (K,) dK, J f ( Kic ) dK .

K I ⁰

Вероятность безотказной работы есть вероятность того, что вязкость разрушения K_IС превысит коэффициент K_I для всех его возможных значений

те

R -J fl (Kc )

-те

K IC

J

-те

f , ( K , ) dK , dK ic .

Принимая во внимание, что вязкость разруше-

ния – положительная величина, а разрушение по I типу раскрытия трещины на практике происходит при больших положительных напряжениях, в двух последних полученных формулах в нижних пределах интегрирования можно вместо « -те » указать «0».

Получим зависимость для оценки вероятности отказа Q исходя из соображения, что возникновение отказа и его отсутствие образуют полную группу событий, то есть R + Q = 1 .

Исходя из свойств плотности распределения можно записать те                         Kj                         те

J f ( K Ic ) dK - J f l ( K Ic ) dK Ic + J f ( K_K ) dK_K - 1 .

-те                        -те                         K j

Следовательно,

те

J f l ( K c ) dK_rc - 1 - F , (K j ),

K I

где F ₁ ( K_I ) – функция распределения вязкости разрушения.

Подставим полученное выражение в формулу для вероятности безотказной работы

те                                                        те

R - J f 2 ( K, )[ 1 - F 1 ( K , ) ] dK , - 1 - J f 2 ( k , ) F ( k , ) dK , ,

-те                                                 -те

и, таким образом, вероятность отказа те

Q - J f 2 ( K , ) F ( K , ) dK , .

-те

Формулу для оценки вероятности безотказной работы можно выразить через функцию распределения коэффициента интенсивности напряжений          _те

R - J f ( K jc ) F ₂( K c ) dK_rc .

-те

Если величины K I и K IС распределены по нор-

мальн о му з акону с математическими ожиданиями K I , K_IC и дисперсиями a K , a K , то их плотности распределений

f 1 ( K jc ) -

a 2^

K IC

- exp

(KIC - KIC )

2 a ²

K IC

те

R = J f 2 ( Ki )

-те

те

J f ( K e ) dK_rc

K I

dK I .

^f 2^{( K}I )---17^ • exp

aK] 2^1

(Ki - Ki)

2 a 2 K_I

Зависимость для оценки вероятности безотказной работы при однократном нагружении можно получить путем интегрирования по K IС :

Введем случайную величину Y = KIС – KI. Она также будет распределена по нормальному закону с математическим ожиданием y - Kc - K, и дисперсией

ст, — ст„ yKIC

+ ст2К

KI

Запишем функцию распределения случайной величины Y , используя нормированную функцию нормального распределения [2]

У ^- У

В случае квазихрупкого разрушения в вершине трещины образуется пластическая область, размеры ее можно оценить поправкой Ир-

вина:

F ( у ) = Ф *

У ^- У

1       ^ст у _- t K

¹ e ² dt .

72 Л -L

Тогда вероятность безотказной работы с учетом нормального закона распределения случайной величины Y

rp rp

1	' K ic
6 л	ст V т	/
1	' K ic
2 л	ст V т	/

– для плоской деформации;

– для плоского напряженного состояния.

R = Pr {y > 0} = 1 - F(0) = 1 - Ф

*

-

y

= 1 - *

V 2 л

y ст

t ²

L

-L

2л

Обозначим

z = - -У сту

^ст у

t ²

J e ² dt . ^{y ст} у

K - Ki

I

и получим выражение для вероятности безотказ-

ной работы              _{L 1} 2

R = f e"⁴dt . 72 Л ^J_z

Поскольку нормальная функция распределения F(y) выражается через функцию Лапласа

F ( y ) = 0,5 + Ф

У ~ У

^СТ у

= 0,5 +

V 2 л

У - У сту

t ²

J e ² dt , 0

вероятность безотказной работы можно представить в следующем виде

R = 0,5 -Ф ( z ),

F ( z ) =

2л

z _- t ²

J e ² dt .

Таким образом, для оценки вероятности безотказной работы при нормальном распределении величин K_I и K_IС н е обх о димо знать их математические ожидания K I , K_IC и дисперсии < r K , ст ^^ . Для вязкости разрушения параметры K_IC и CT K, определяются экспериментальным путем, поскольку они являются характеристиками мате р иала.

Найдем формулы для определения K I и CT K при условии, что известны математические ожидания и дисперсии действующих н омина л ьных напряжений о и длины трещины l : CT , ст СТ , l , ст ₁ ².

На основании выражения (1) и с использованием метода статистической линеаризации получим

K i = Y i CT^^ T ,            (4)

^CT K I

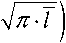
2 .

СТст + YCT

^CT 1 ².

Таким образом, при определении K I следует использовать «условную» длину трещины, увеличивая начальную длину на величину r_p , то есть l + r_p . Поскольку длина трещины значительно превышает величину поправки r_p , можно принять допущение о ее детерминированности. Тогда математическое о жидание длины трещины определится суммой l + r p , а ее дисперсия не изменится.

ПРИМЕР ОЦЕНКИ ВЕРОЯТНОСТИ БЕЗОТКАЗНОЙ РАБОТЫ

В качестве примера приведем расчет нагружения устройства защиты оператора гусеничного трелевочного трактора «Онежец 300» боковой силой F = 70 кН (согласно требованиям ИСО 8082). Поскольку ИСО 8082 допускает при испытаниях использование распределителей боковой нагрузки, имеющих длину до 80 % горизонтального расстояния между передней и задней стойками ROPS, можно сделать допущение о плоском напряженном состоянии конструкции. Рассмотрим три варианта возникновения трещин следующих типов: сквозной, полуэллиптической и граничной краевой. Схема образования трещин представлена на рис. 1.

Материал ROPS – сталь 15ХСНД с пределом прочности σ В = 800 МПа, пределом текучести σ Т = 380 МПа и критическим коэффициентом интенсивности напряжений K_IC = 44,6 МПа • V м [5]. Моделирование напряженно-деформированного состояния ROPS «Онежец 300» было проведено автором в работе [7]. С использованием метода конечных элементов и программы «Зенит» оценена интенсивность механических напряжений. Поскольку зонами максимальных напряжений о *¹™ = 715 МПа являются зоны задних опор для установки ROPS на раме трактора [7], оценку вероятности безотказной работы проведем при допущении о возможном месте локализации трещин в зоне максимальных напряжений (рис. 2).

Величина коэффициента K_I вычислялась по формуле (1) при следующих функциях Y I (l) [5]:

• •    для граничной краевой трещины – Y I (l)= 1,1215;

• •    для сквозной трещины – Y I (l) = 1,0;

• •    для полуэллиптической трещины –

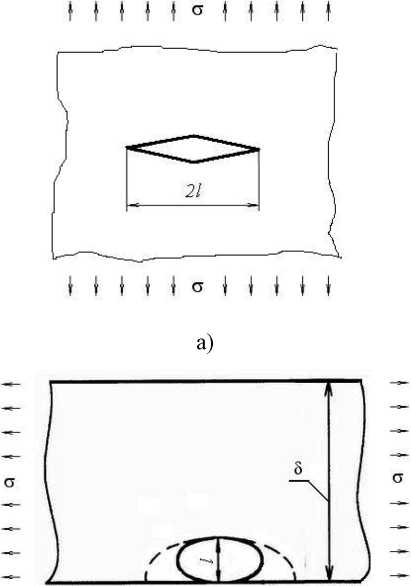
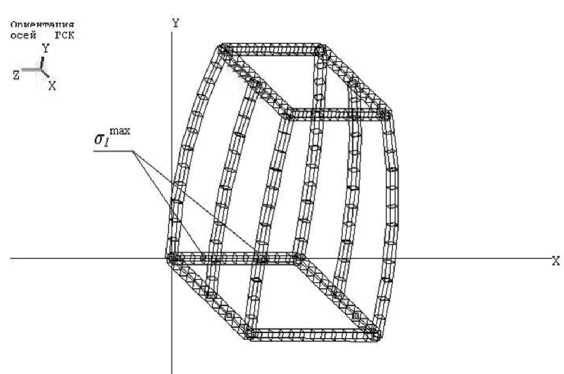
Рис. 2. Конечно-элементная модель ROPS «Онежец 300»

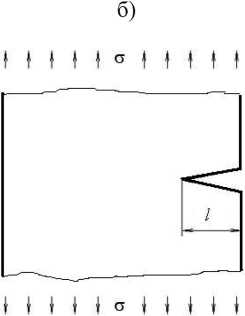
в)

Рис. 1. Схемы образования трещин: а) сквозной; б) полу-эллиптической; в) краевой

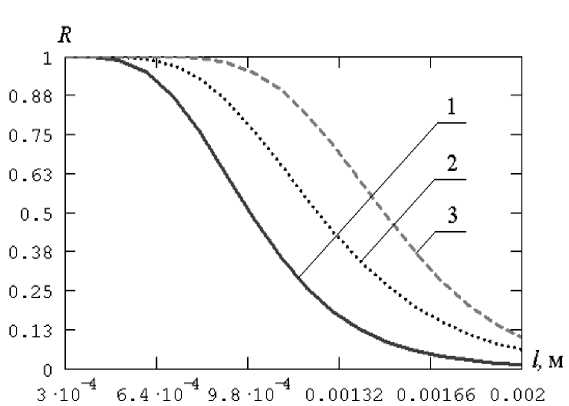
Рис. 3. График зависимости вероятности безотказной работы ROPS от длины и вида трещины: 1 – краевая;

2 – сквозная; 3 – полуэллиптическая

Y, ( l ) =

0,8

1 - 0,5 ^- , 5

где δ – толщина стенки профильной трубы, δ = 8 мм.

Таким образом, исходные данные для расчета по формулам (2)–(5):

a = 715 МПа; K C = 44,6 МПа • 4м ; Г = l

а = 0,1 a ; а = 0,1 K,_г ; a = 0,1 - . [6] a K ,c ,C l

Результаты расчета вероятности безотказной работы устройства защиты оператора в зависимости от длины и вида трещины представлены на графике (рис. 3).

ВЫВОДЫ

Технологические дефекты в виде несплош-ностей, раковин, неметаллических включений, рисок от механической обработки и т. п., присутствующих в реальных материалах еще до начала эксплуатации, влияют на прочность конструкций и могут рассматриваться как элементы начала разрушения. Методика, представленная в данной работе, позволяет проводить оценку вероятности безотказной работы при однократном нагружении ROPS лесозаготовительной машины. Расчет проведен на примере ROPS гусеничного трелевочного трактора «Онежец 300» для варианта возможной локализации в зоне максимальных напряжений трещин следующих видов : сквозной, граничной краевой, полуэллиптической. Как следует из результатов расчета, наличие дефектов в виде трещин, даже небольшой величины, существенно снижает вероятность безотказной работы.

* Работа выполнена при поддержке Программы стратегического развития (ПСР) Петрозаводского государственного университета в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012– 2016 гг.

ESTIMATION OF FOREST MACHINE ROPS RELIABILITY IN TERMS OF FRACTURE MECHANICS