Оценка вероятности обнаружения мультимедиаконтейнеров при пространственно-временном распылении информации
Автор: Алексеев Александр Петрович, Блатов Игорь анатольевиЧ., Макаров Максим Игоревич
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Электромагнитная совместимость и безопасность оборудования
Статья в выпуске: 3 т.11, 2013 года.
Бесплатный доступ
В статье приведена оценка вероятности обнаружения различных мультимедиаконтейнеров в телекоммуникационных сетях при пространственновременном распылении информации.
Стеганография, поисковый робот, пространственно-временное распыление информации
Короткий адрес: https://sciup.org/140191654
IDR: 140191654 | УДК: 681.322
Текст научной статьи Оценка вероятности обнаружения мультимедиаконтейнеров при пространственно-временном распылении информации
Постановка задачи
При скрытой передаче информации методом пространственно-временного распыления [1] злоумышленник может перехватить передаваемое сообщение. Одной из проблем, с которой столкнется криптоаналитик, будет необходимость обнаружения Web-страницы, содержащей конфиденциальное сообщение.
В качестве примера рассмотрим процесс обработки новых Web-страниц поисковыми системами в сети Internet. Для индексации страниц применяются специализированные программы - поисковые роботы [2]. Нет опубликованных данных о том, с какой частотой роботы выполняют опрос узлов и за какое время они находят новые серверы, так как эти сведения являются коммерческой тайной владельцев поисковых систем. Допустим, что вычислительные ресурсы злоумышленника позволяют ему использовать собственный поисковый робот, который в случае обнаружения нового узла сети (сервера или сайта) включит его в список (индексирует) для последующей проверки на наличие обновлений.
Пусть на промежутке [0; ,τ] с интенсивностью λ в сети размещается (публикуется) на короткое время ∆ t << τ Web-страница (контейнер) с конфиденциальной информацией ( λ – математическое ожидание числа появлений страницы в единицу времени). В силу стационарности, ординарности и отсутствия последствия можно считать, что появления в сети этого контейнера образуют пуассоновский поток с интенсивностью λ . Робот сканирует узел сети с периодом T >>∆ t за короткое время (близкое к нулю), и момент сканирования является случайной величиной, равномерно распределенной на интервале [0,τ]. Требуется определить: с какой вероятностью робот обнаружит эту Web-страницу.
Решение
Если мультимедиаконтейнер может с равной вероятностью появляться в одном из m каналов стегосистемы, то это означает, что при многоканальной передаче информации интенсивность λ нужно разделить на m , то есть достаточно рассмотреть модель с одним каналом и интенсивностью λ / m .
Пусть X – случайная величина, равная числу появлений Web-страницы за время [0; τ]. Согласно распределению Пуассона
P{X^k> = Ur/ е”Лт. (1)
1 ' kl
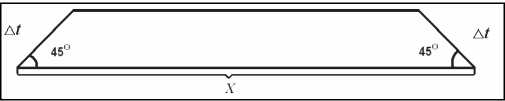
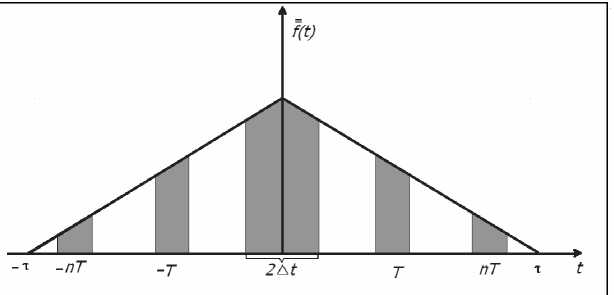
Рис. 2. Фрагмент предыдущей фигуры
Обозначим через q k вероятность события A , состоящего в обнаружении контейнера роботом при условии, что за время τ контейнер появился (был размещен в сети) k раз. Тогда по формуле полной вероятности будем иметь:
Найдем площадь заштрихованной фигуры (см. рис. 2):
„ 2x-KtJl Kt Kt 1,.
8,„= ------у = х-^=--(Д/) .
VW = t^e-*'qi. (2)
к=А К '
Таким образом, задача сводится к отысканию величины q k. Рассмотрим вначале частные случаи.
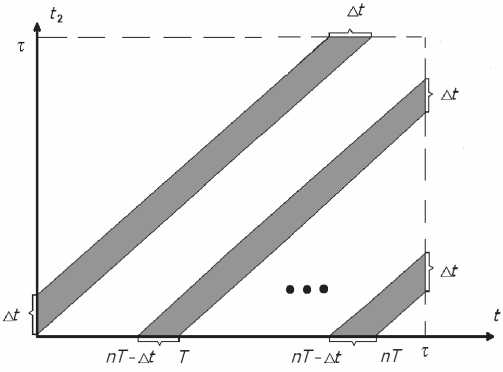
Рис. 1. Иллюстрация к определению вероятности при k = 1
Для заштрихованных трапеций стороны х определяются выражением:
х = rV2,(r-T + К^41,...,^т-пТ + Kt\j2.
Суммарная площадь заштрихованных фигур составляет:
S = Kt^c + (г -Т + А/) + ... + (г-иГ + А/))- й + 1 (AZ)2 =
— ((и + 1)г--- —T^Kt + z?(A?)"-— (Az) —
=(»+i)(r-^m+^(A/)2.
Отсюда
^ = 4 - 4 (« + l)(r - у Т)Kt + 44 (AZ) =
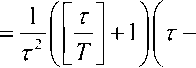
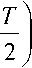
A/ + O((AZ)2). (3)
1. Контейнер размещается в сети за время наблюдения один раз ( k = 1). В этом случае отыскание q 1 ведется из геометрического определения вероятности и иллюстрируется следующим рисунком.
Заштрихованные области соответствуют неравенствам:
2. Контейнер размещается в сети за время наблюдения два раза ( k = 2). Страница появляется дважды – в моменты времени t 1,1 и t 1,2. Значит, площади, соответствующие первому и второму появлению, не будут пересекаться, если выполнено условие
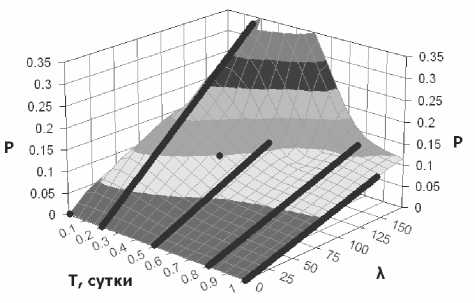
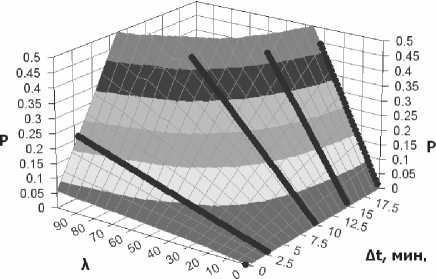
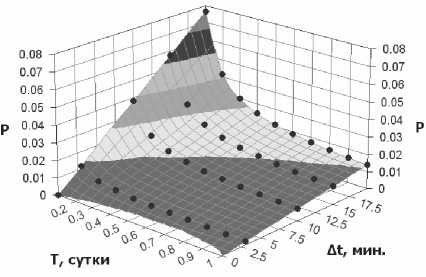
О 2—^1 |z, 2-t} J > A/(modT). О < h - (Zi - и 7) < А/, где t1 – время появления контейнера в сети, а t2 – время первого захода робота на страницу. Здесь и = т Т – число заходов робота на стра- ницу за промежуток времени длительностью τ (квадратные скобки означают взятие целой части числа). В этом случае события обнаружения роботом первого и второго контейнера несовместны. При выполнении условия (4) мы получим, что q2=2q1. Найдем вероятность выполнения условия (4). Если моменты появления заявок распределены по равномерному закону с плотностью: /и^Р'е[0'г1; O,Z^ [О, г], то случайная величина (–t1) так же распределена по равномерному закону на интервале [0; τ] с плотностью ^ ^, 3_t] ,|>A/(mod7-)^) ' ^0 ?1,2 Zl,l >^mo^Pv^ |< /ю= -,^e[0, г] i т Az(modT)) = — г Т т- L L Т 2 AZ 0,Z ^[0,г] 2 2 f т О- — Д0 + О((А/)") = — — +1 т - - A/ + O((AZ)2). Т 2 Разность величин t2 – t1 распределена на интервале [–τ; τ] с плотностью Аналогично при произвольном k можно показать, что 7(0=(/*/хо = j/w/o -^=j/w/o -^= A A + 1 T- AZ + O((Az)2).(5) = Л \fU - ^dx = ^ j f(u)du = 0 Из формул (2) и (5) получаем решение нашей задачи в виде: т — t,t е [0, г] г+ Z,Z е [-г,0] = 0,Z £ [-г, г] г —|z|,Z g [-г, г]; 0,Z g [-г, г]. Л^)=- - r\ T t^J^ k\ eATk^O(W\ или же Поэтому (см. рис 3): 1,2 М f^dt = А/ Г+А/ _ О Т-Ы пТ+^ _ J 7(0^ ^ пТ-Ы т _ А Az( т V т Т ЛЛ=— — +1 м— ■ Г\ Т Д Г 2 г( I и, окончательно, - ЯгУ- к=О М^+^2), Р<А>- - +1 т--- AN+О^МП (6) т \ Т Д Т 2 т 2 2 < —пМ< —Az. т т Вероятность выполнения (4) будет не меньше, чем — AZ.По формуле полной вероятности будем иметь: При практическом применении формулы (6) слагаемое O((AZ)2) отбрасывается, и мы получаем приближенную формулу [3]. Данная формула имеет высокую точность при малых 2AZ. Для удобства расчетов за единицу времени можно выбрать сутки. Если положить τ = 1, то, например, при условии, что Web-страница размещается в сети на время, равное трем минутам, будем иметь Az =------—---, Я – среднее число появлений 20-24 480 Рис. 3. Иллюстрация к определению вероятности при к = 2 контейнеров в сутки, T – период захода робота на страницу, измеряемый в сутках, и формула (6) примет вид: W)= л Последняя формула при 2 = 2; Г = 0,25 дает значение вероятности обнаружения роботом размещенной в сети Web-страницы Р(Л) = 0,01. Были произведены расчеты вероятности обнаружения контейнеров для различных периодов опроса роботом страницы, интенсивности ее демонстрации Рис. 6 Вероятность обнаружения контейнера при ∆t =1 мин и продолжительности размещения страницы в сети. На рис . 4 представлен график зависимости вероятности обнаружения роботом страницы от числа ее появлений в сутки λ и времени демонстрации страницы ∆t, при опросе роботом узла сети один раз в сутки. Рис. 4. Вероятность обнаружения контейнера при T = 1 сутки Рис. 5. Вероятность обнаружения контейнера при λ = 1 На рис. 5 отображена зависимость вероятности обнаружения роботом контейнера при изменении длительности демонстрации страницы ∆t и периода опроса роботом страницы Т. На рис. 6 показано влияние на вероятность обнаружения контейнера интенсивности размещения страницы в сети и периодичности посещения роботом страницы. Анализ полученных данных показывает, что для снижения вероятности обнаружения контейнера нужно уменьшать время демонстрации страницы и интенсивность его публикации. Для снижения интенсивности демонстрации страницы предлагается применять многоканальную передачу, за счет чего можно уменьшать частоты появлений контейнеров в каждом канале. Выводы Полученные результаты показали, что для уменьшения вероятности перехвата скрытно передаваемых данных следует снижать до минимума время нахождения контейнеров в сети и использовать множество каналов передачи данных, тем самым снижая частоту их демонстрации.
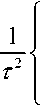

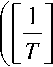
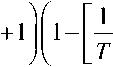
Список литературы Оценка вероятности обнаружения мультимедиаконтейнеров при пространственно-временном распылении информации
- Алексеев А.П., Макаров М.И. Принципы многоуровневой защиты информации//ИКТ. Т.10, №2, 2012. -С. 88-93.
- Маннинг К., Рагхаван П., Шютце Х. Введение в информационный поиск.: Пер. с англ. М.: ООО «И. Д. Вильямс», 2011. -528 с.
- Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М.: Физматлит, 1962.-607 с.


