ОЦЕНКА ВЕРОЯТНОСТИ ОШИБОЧНОЙ ИНТЕРПРЕТАЦИИ РЕЗУЛЬТАТОВ ПЦР-АНАЛИЗА. Ч. 1. ОТКАЗЫ ТЕХНИЧЕСКИХ УСТРОЙСТВ

Оценка вероятности безотказной работы прибора или/и связанного с ней времени средней наработки до первого отказа, очевидно, имеет большое практическое значение. Имеется достаточно большое число работ, описывающих различные вероятностные модели отказа технических устройств (элементов), параметров распределений, в т.ч. и характерных времен наработки на отказ, средних времен до первого отказа или между отказами, интенсивностей отказов и т.п. Однако в большинстве случаев интересы авторов касаются именно указанного набора оценок и вероятностей отказов при условии продолжительной эксплуатации оборудования.

В данной работе на основе известных статистических моделей, оценок характерных времен или интенсивностей отказов рассматривается случай малых времен непрерывной работы устройства для количественного генетического анализа методом полимеразной цепной реакции в реальном времени (ПЦР-РВ). Малые времена — времена, не превышающие среднего времени до первого отка- за наименее надежного элемента или блока, которые далее будут называться "слабым звеном". В наших условиях эти времена составляют сотни часов непрерывной работы.

Принципиально важным представляется невозможность дублирования любого элемента. При этом его отказ или нештатная работа приводит к получению некорректного результата анализа.

При получении количественных оценок вероятности некорректного результата анализа по причине отказа элементов прибора, рассматриваются следующие основные аспекты и ограничения.

Первый аспект — исследование зависимости оценок вероятности отказа от вида закона распределения. При этом ограничиваемся классом распределений Вейбулла с различными показателями, а другие вероятностные модели, например усеченное нормальное и логнормальное распределения не рассматриваются. Наиболее известное и часто используемое модельное вероятностное распределение — экспоненциальное — относится также к распределениям Вейбулла (параметр равен 1).

Второй аспект связан с тем, что часто в расчетах, например, при построении таблиц функций неисправностей и связанных с ними моделей поиска ошибок применяется схема отказа только одного элемента. В связи с этим требуется определить, во-первых, в какой мере некорректность результатов анализа связана с отказом "слабого звена", во-вторых, насколько обоснована гипотеза отказа только одного элемента (или блока), и, наконец, сколь обоснованно предположение о наибольшей вероятности отказа только "слабого звена" без сопровождающих его отказов других элементов. Естественно, описывается примерный набор элементов прибора и выявлено его "слабое звено".

В первой части статьи не учитываются эффекты, связанные непосредственно с постановкой и проведением ПЦР-РВ, корректностью обработки информативного сигнала (кривой ПЦР), а также интерпретацией результата.

Кроме того, не учитывается аспект, связанный с наличием человеческого фактора. Известно, что при 6-часовой рабочей смене без необходимости выполнения сложных операций, отсутствии жестких требований по быстродействию и при проведении предварительных 4 тренировок, вероятность ошибки из-за человеческого фактора примерно равна 0.9% [1]. Эти аспекты будут рассмотрены в следующих частях статьи.

ИСХОДНЫЕ ДАННЫЕ И РАСЧЕТНЫЕ ФОРМУЛЫ

Выражение для плотности распределения вероятностей, содержащее положительный параметр k , определяется формулой (1)

f ( x ) = X - kx k ^{- 1}exp ( - ( x / X)^k ) . (1)

Эта зависимость описывает класс распределений Вейбулла. При этом масштабный параметр λ связан со средним временем до первого отказа, х — время. Величина, обратная λ , определяет интенсивность потока отказов. Если k больше 1, то интенсивность отказов возрастает со временем. В случае k = 1 получается экспоненциальное распределение.

Математическое ожидание времени до первого отказа при вероятностной модели (1) есть m = ХГ(1 +1/ k). (2)

В формуле (2) символ Г обозначает гамма-функцию.

Сравнение вероятностей отказов для разных законов (соответствующих различным k ) проводится, исходя из равенства среднего времени отказа (первого отказа) прибора, которое определяется формулой (3):

Ф ( x ) = 1 - exp ( - ( x / X) ^k ) . (3)

В связи с этим проводится пересчет параметра λ , согласно (2).

"Слабое звено" — это блок (элемент) с наибольшей вероятностью отказа к рассматриваемому времени 700 или 1000 часов. Очевидно, что соответствующий параметр распределения λ должен быть наименьшим. Вероятность отказа обратно пропорциональна λ только на очень малых временах работы, в условиях, когда выполнено 1 - exp ( - x / X ) ® x / X , а это отношение имеет порядок несколько сотых. Например, для x / λ = 0.0500 в левой части предыдущего приближенного равенства стоит 0.04877, для x / λ = 0.0300 получаем 0.02955.

Если в качестве события А рассматривать отказ блока или прибора в целом, то вероятность сопровождающего его отказа какого-либо элемента при условии достижения отказа прибора (блока) — апостериорная вероятность, рассчитываемая по формуле Байеса:

P (H|A) = P (AH)/ P (A).

Здесь событие А — отказ схемы, Н — отказ элемента, например, "слабого звена", АН — отказ схемы, сопровождаемый отказом "слабого звена". Указанная формула показывает, в какой мере отказ схемы связан с отказом именно "слабого звена", поскольку причины общего отказа схемы могут быть и иными и объясняться отказом других элементов.

Общая схема прибора для реализации ПЦР-РВ может быть сведена к виду, представленному на рис. 1. Блоки и их функции кратко описаны в тексте после рис. 1.

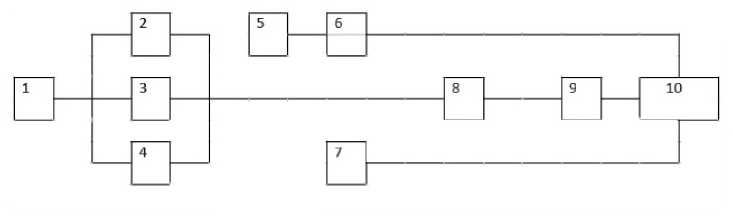
Рис. 1. Укрупненная схема прибора для количественного генетического анализа методом ПЦР-РВ (пояснения в тексте)

Данная укрупненная структурная схема прибора не детализирует особенностей его конструкции, не раскрывает иных аспектов, которые могли бы содержать элементы "know-how". Она иллюстрирует общий принцип измерений, отражая соответствующие логике функционирования связи между блоками. Блок 1 "Питание" представляет очевидную закономерность — при его отсутствии невозможно проведение корректного анализа по причине неработоспособности последующих блоков 2– 4. Блок 2 — "Блок пробоподготовки", 3 — "Оптический блок" и 4 — "Тепловой блок". Последний должен обеспечивать требуемое циклическое изменение температуры в пределах 60–95 оС с определенной продолжительностью каждой фазы. Условно названная блоком 5 "Установка картриджа" предполагает обеспечение требуемого позиционирования планшета или картриджа с пробирками, содержащими анализируемые пробы. Очевидно, что ошибочное позиционирование картриджа приведет к неэффективному проведению ПЦР либо вообще к невозможности ее проведения. Блок 6 "Сигнал ошибки установки картриджа" подтверждает правильность позиционирования картриджа. Отказ выполнения операции по отображению этого сигнала приведет к тому, что будут рассмотрены результаты анализа при ошибочном размещении проб в приборе. Тем самым очевидно, что результат анализа будет неверным. Кнопка 7 "Ручное отключение" позволяет прервать цикл анализа при явном нарушении штатных условий его проведения. Соответственно, несрабатывание этой кнопки приведет к учету результатов анализа, проводимых в неприемлемых условиях. В целом отказы блоков (устройств) 5–7 приведут к ошибочному учету результата анализа, проведенного в недопустимых условиях. Блок 8 "ПК" — персональный компьютер — осуществляет управление другими блоками и элементами, например 2–4, а также с его помощью обеспечивается выход результата анализа 10.

Элемент 9 — анализ пробы в рамках рассматриваемой приближенной расчетной модели считается идеально функционирующим, не имеющим никаких погрешностей в работе. Т.е. в число возможных источников (причин) некорректного результата анализа, в т.ч. по причине отказа блока или элемента, некорректный анализ пробы и его ошибочная интерпретация не входят. Блок 10 представляет собой конечную точку, в которой фиксируется результат анализа, корректно или некорректно полученный.

Задав в качестве событий A i события, связанные с безотказной работой соответствующих блоков, а события А — безошибочную интерпретацию анализа, событие А может быть записано как

А = А 1 А 2 А 3 А 4 А 8 + А 5 А 6 + А 7 . (4)

События, входящие в (4), являются независимыми, но могут быть совместными. Т.о. вероятность произведений будет произведением соответствующих вероятностей, а вероятность суммы считается по формуле суммы 3 совместных слагаемых, не имеющих общих множителей.

Вычисление вероятностей будет проходить в два этапа: вначале вычисляется вероятность отказа оптического блока 3, как "слабого звена" среди блоков, а затем вероятность отказа к заданному времени (от 100 до 1200 ч непрерывной работы) прибора в целом.

Расчет строится на распределении Вейбулла с параметром 1 (экспоненциальное распределение).

РАСЧЕТ ВЕРОЯТНОСТЕЙ ОТКАЗА ДЛЯ ОПТИЧЕСКОГО БЛОКА

Состав оптического блока: ФЭУ, 3 шаговых двигателя с оптопарами, 5 светофильтров и светодиод. Это основные элементы, максимально "обезличенные". Для дальнейших расчетов используются средние значения времени до первого отказа либо пересчет данных по интенсивности потока отказов.

Т.к. ни один из элементов не дублируется, для корректной работы блока необходима безотказная работа всех элементов. Исходные данные были представлены в двух форматах: среднее время до первого отказа в часах либо интенсивность потока отказов, являющаяся обратной величиной по отношению к среднему времени отказа или, что то же самое для экспоненциального распределения, параметру распределения λ . При наличии нескольких элементов, выполняющих одну функцию, например шаговых двигателей, светофильтров и т.п., интенсивности потоков отказов суммируются.

Необходимые исходные данные для расчета вероятностей отказов элементов оптического блока и методика расчета взяты из учебного пособия [2], в котором, в свою очередь, использованы сведения из [3–10]. Очевидно, для оптического блока "слабым звеном" является ФЭУ. Далее на рис. 2 представлен график вероятности отказа оптического блока при временах непрерывной работы 100– 1200 ч.

В табл. представлены литературные данные по времени непрерывной работы отдельных элементов или связанные с ними значения интенсивности потока отказов.

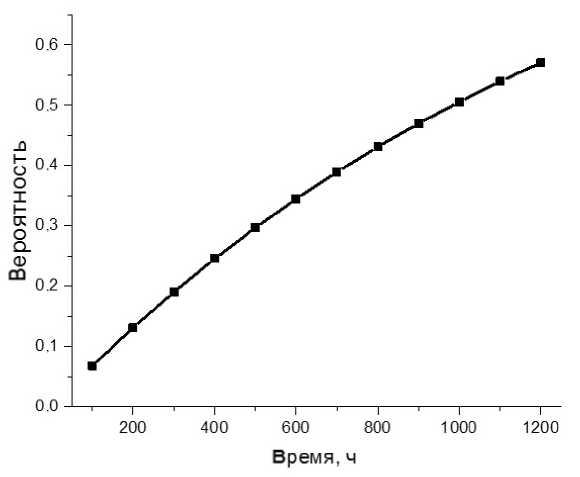
Табл. Расчетные данные по надежности элементов прибора

Рис. 2. Вероятность отказа оптического блока при различных временах непрерывной работы

Элемент	Среднее время до первого отказа, ч
Фотоэлектронный умножитель (ФЭУ)	2.0·103
Светодиод	(15 ^ 25)^10 3
Оптопара	(10 ^ 20)^10 3
Светофильтр (интерференционный)	3.3·105
Элемент Пельтье	2.0·105
Нагреватель	1.3·105
Шаговый двигатель (ШД)*	2.7·106
Компьютер**	9.85·103
Ручное отключение	1.0·107
Блок 6 (аналог жидкокристаллического индикатора)	2.5·104

* — как обратная величина от интенсивности потока отказов;

** — пересчет на основе вероятности отказа за год непрерывной работы.

Исходные данные взяты преимущественно из [2], а также из [3, с. 280–284], [4–10], в которых содержится информация о характеристиках надежности элементов и приборов разных типов: оптико-электронных [7–9], тепловых, механических [6] и т.п. В табл. представлены среднее значение либо диапазон значений, а расчет проводится на основе среднего времени наработки до первого отказа. В частности, для разных типов ФЭУ указан достаточно большой диапазон времен в пределах 500–10000 ч [4]. Для оценок интенсивности отказов механических элементов используются данные для зубчатых передач (0.11–0.36)·10–6 1/ч [5] и берется среднее значение 0.25·10–6 1/ч.

Детальный расчет вероятности отказа ПК при непрерывной работе 1 год, т.е. 8760 ч, дает 0.89, что выражено через отказы основных элементов: системной платы, RAM-модулей 1 и 2, вентилято- ров 1 и 2, блока питания [10]. Отсюда по экспоненциальному закону вычислен параметр распределения (3), указанный в табл.

Т.к. для работоспособности оптического блока необходимо отсутствие отказов всех элементов, то при ограничительном условии независимости отказов соответствующая вероятность будет произведением вероятностей безотказной работы элементов. Далее рассматриваются: апостериорная вероятность отказа именно ФЭУ ("слабого звена") при условии отказа оптического блока, а также вероятность отказа только одного элемента (любого) при условии безотказной работы всех остальных элементов.

Зависимость на рис. 2 с учетом перевода в проценты хорошо аппроксимируется параболой вида:

P (%) = 0.553 + 0.066 1 - 1.591 • 10 ^{- 5} 1 2 . (5)

Здесь t — время непрерывной работы в часах. Коэффициент детерминации зависимости превышает 0.99, что свидетельствует о высоком качестве аппроксимации. На малых временах зависимость близка к линейной.

Далее на рис. 3 представлены зависимости от времени непрерывной работы вероятности отказа ФЭУ как "слабого звена" оптического блока, так и вероятности отказа только одного элемента при условии отказа блока. Логика последнего случайного события упрощена, т.к. отсутствует дублирование элементов: отказ одного элемента сопровождается безотказной работой остальных элементов, а соответствующие слагаемые, состав-

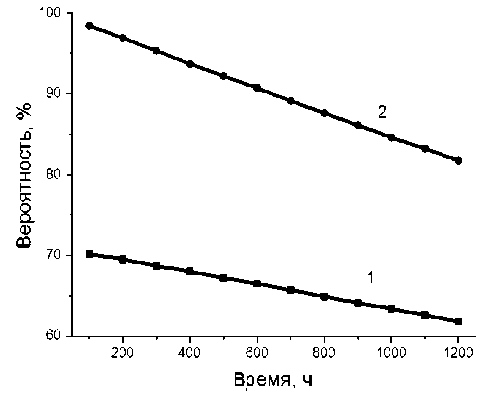
Рис. 3. Вероятности отказа (1) ФЭУ, (2) только одного элемента при условии отказа оптического блока ляющие суммарное событие "отказ одного элемента", оказываются несовместными.

Обе зависимости носят характер, близкий к линейному убывающему. Рассматриваемые времена существенно меньше среднего времени первого отказа "слабого звена" — ФЭУ — и тем более многократно меньше средних времен первого отказа остальных элементов блока.

При этом даже при очень малых временах непрерывной работы понятие "слабого звена" достаточно условно, т.к. в 30–40% случаев отказ блока связан с отказом не "слабого звена", а других элементов.

РАСЧЕТ ВЕРОЯТНОСТИ ПОЛУЧЕНИЯ НЕКОРРЕКТНОГО РЕЗУЛЬТАТА АНАЛИЗА

В качестве единственной причины некорректного анализа в этой Ч. 1 статьи рассматривается отказ элементов (блоков), вызывающий либо невозможность проведения ПЦР-РВ, либо отказ в фиксации аномальных условий проведения анализа, к которым относится некорректное размещение картриджа с пробами и отсутствие информации об этом, а также неосуществимость ручного завершения анализа по решению оператора.

Аспекты, связанные с неэффективным и некорректным проведением собственно ПЦР (блок 9), а также с человеческим фактором, будут проанализированы в следующей части статьи.

Методика расчета вероятности отказа прибора ориентирована на формулу (4), которая выражает вероятность противоположного события — вероятность безотказной работы. Динамика условной вероятности отказа оптического блока как "слабого звена" прибора в целом иллюстрируется рис. 4.

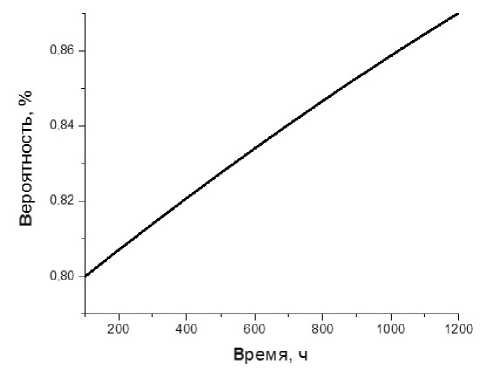
Рис. 4. Условная вероятность отказа оптического блока при отказе прибора

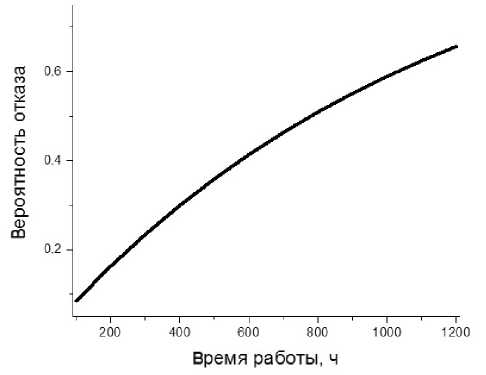
Рис. 5. Вероятности отказа хотя бы одного из блоков прибора

На рис. 5 приведена зависимость вероятности отказа хотя бы одного из блоков прибора, следствием чего является отказ прибора в целом и, естественно, некорректный результат анализа.

Условная вероятность отказа именно оптического блока меняется по закону, близкому к линейному, и в очень небольшом диапазоне значений (80–87%). Тем самым фактор оптического блока как "слабого звена" прибора (блока, а не отдельного элемента) подтверждается. График на рис. 5 свидетельствует о том, что в условиях относительно небольших времен непрерывной работы (порядка месяца, т.е. примерно 700 ч) вероятности отказа могут превышать 40%.

ТАБЛИЦА ФУНКЦИЙ НЕИСПРАВНОСТЕЙ

Таблица функций неисправностей (ТФН) является признанной, достаточно универсальной математической моделью объекта диагноза и принадлежит к классу явных моделей. Ее построение служит важным этапом синтеза алгоритма тестирования устройства, целью которого является разработка схем выявления неисправного элемента на основе формирования выборки тестовых сигналов и их анализа. Методология формирования ТФН описана, например, в работах [11–17].

Процесс построения логической модели состоит из следующих этапов [11]:

• 1.    В системе выделяют отдельные функциональные элементы, входы и выходы которых доступны для измерения.

• 2.    Для каждого элемента указывают диапазоны допустимых входных и выходных воздействий.

• 3.    Составляют функциональную схему, содержащую выделенные элементы и связи между ними.

• 4.    Выявляют возможные состояния системы.

• 5.    Составляют ТФН.

В подавляющем большинстве случаев ТФН строится, исходя из гипотезы, что происходит отказ (неисправность, некорректная работа) только одного элемента. В других случаях построение ТФН усложняется многократно. Как показывают оценки предыдущего раздела, доля случаев, когда происходит отказ не единственного элемента или блока, достаточно велика (до 30–40%).

ЗАКЛЮЧЕНИЕ

Все представленные оценки характерных вероятностей некорректной работы оптического блока и прибора в целом и методология расчетов практически не зависят от параметра распределения k в формуле (1). Количественные оценки базировались только на одном варианте распределения Вейбулла с параметром 1 (оно же экспоненциальное).

Закономерности, выявленные ранее, свидетельствуют об относительной условности понятия "слабого звена": вероятность отказа указанного элемента или блока лишь на 60–70% является причиной отказа прибора в целом; гипотеза отказа единственного элемента также не всегда правомерна, в особенности для времен более 20% от среднего времени до первого отказа. Эти закономерности будут, скорее всего, проявлены и при использовании других вероятностных моделей отказа из класса распределений Вейбулла.

В то же время количественные значения вероятностей отказа будут уменьшаться при увеличении параметра k , что проиллюстрировано графиком на рис. 6.

Относительное (безразмерное) время нормировано на среднее время до первого отказа. Соответственно подбирается параметр распределения Вейбулла. Известно, что модель (1) при k = 1 соответствует случаю экспоненциального распределения; для распределений, соответствующих параметрам 1.5 и 2, свойственно увеличение вероятности отказа элементов со временем. В частности, применительно к ФЭУ со средним временем до первого отказа 2000 ч, время непрерывной работы 1 месяц или около 700 ч соответствует относительному времени около 0.3. Видно, что для вероятностной модели с k = 2 вероятность отказа уменьшилась примерно вдвое по сравнению с экспоненциальным распределением k = 1. В то же время плотность распределения вероятностей (1) для параметра k = 2 при больших рассматриваемых вре-

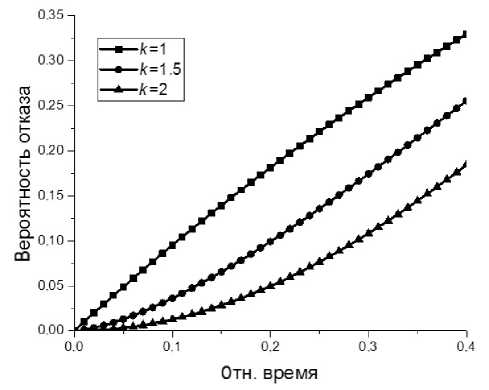
Рис. 6. Вероятности отказа прибора в зависимости от параметра распределения Вейбулла менах существенно больше, чем для аналогичной зависимости при k = 1 даже с учетом согласования параметра λ, исходя из равенства математических ожиданий времен отказа (2).

Определение значения параметра k , наиболее соответствующего схемам отказа элементов реальных приборов, требует специального обследования на репрезентативной выборке серийно выпускаемых приборов достаточно большого объема, поскольку чувствительность вероятностных оценок к изменениям параметра k достаточно мала.

Следовательно, выявленные закономерности по изменению вероятностей отказов элементов и блоков приборов для малых времен работы, связанные с условными и апостериорными вероятностями, могут быть использованы для различных оценок, связанных с вкладами т.н. "слабых звеньев". При этом для использования абсолютных оценок вероятностей потребуется верификация вероятностных моделей (1), как минимум связанная с адекватным выбором параметра k .

Аспекты, связанные с некорректным проведением собственно ПЦР-РВ (блок 9), а также с учетом человеческого фактора, предполагается рассмотреть во второй части данной работы.

Работа выполнена в рамках Государственного задания Министерства науки и высшего образования Российской Федерации № 075-01157-23-00 (тема FFZM-2022-0012).