Оценка вязкости разрушения сталей по результатам контактного деформирования

Увеличение прочности, как правило, сопровождается снижением пластичности и вязкости разрушения. Это происходит потому, что у высокопрочных материалов мала энергия, поглощаемая при разрушении. Уровень этой энергии при хрупком разрушении определяется размером пластической зоны перед фронтом трещины (см. рис. 1). Если при внедрении индентора в поверхность контртела в зоне контакта возникает остаточная вмятина, то вокруг нее всегда имеется пластически деформированная область, распространяющаяся на некоторую глубину h_s (см. рис. 2). Эта область ограничена замкнутой поверхностью, на которой удовлетворяется условие пластичности Генки – Мизеса ( s _i = s _T ). Наблюдаемое при повышении прочностных свойств, снижении температуры, увеличении скорости деформации уменьшение пластически деформированного объема (а значит, и работы пластической деформации) при испытании на твердость и вязкость разрушения есть следствие одного и того же явления – снижения подвижности дислокаций.

В работах [2–4] был предложен метод расчета удельной энергии пластической деформации gр в малой пластической зоне перед фронтом трещины. Показано существование зависимости между коэффициентом интенсивности напряжений КIc и gр в широком интервале температур для сталей разных уровней прочности. Если между энергетическими параметрами пластических зон при вершине трещины и при вдавливании сферического индентора будет установлена связь, то появится возможность прогнозирования сопротивления хрупкому разрушению по результатам контактного деформирования материалов.

Глубину распространения пластической зоны при вдавливании сферического индентора h_s находили по формуле:

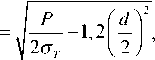
где Р – приложенная нагрузка;

s _Т – предел текучести материала полупространства;

d – значения диаметров полученных отпечатков.

Для построения обобщенной кривой течения s _i = f ( e _i ) в пластической зоне под отпечатком вдоль оси вдавливания следует рассчитать текущие значения интенсивности напряжений в центре контакта s _i при каждом значении нагрузки. В работе [5] величину интенсивности напряжений в центре контакта s _i было предложено определять как

1,5 Ap ₀ ε _i            ,

3s , + exp [- 1,5 s , 0 + C ( z - R ) ]

где р ₀ – давление в центре контакта;

s _Т – предел текучести материала полупространства;

R – радиус индентора;

e _i – интенсивность упругопластической деформации.

Интенсивность упругопластической деформации определяется по формуле ei = k • h • exp(-k • z),             (3)

где k – параметр, характеризующийся упругими свойствами материала;

h – глубина отпечатка.

Давление в центре контакта рассчитывается как ui

<Г _Т + CT-

—T----i - x ^

2 i ,

где s _i и e _i – текущие значения интенсивности напряжений и деформаций вдоль оси z по глубине распространения пластической зоны при вдавливании, рассчитанные по известным зависимостям.

Интегрируя зависимость u_i ( x ) от 0 до h_s , по формуле (7) получаем значение удельной энергии пластической деформации по глубине пластической зоны при вдавливании сферического индентора:

P 0 =

1 + 0,5 a | HM, ^, D J ^,

U p

h _s

= j uidx.

где а – радиус площадки контакта; НМ – твердость по Мейеру.

Постоянные А и С определяются как

=              hs3             , lnhsR+R (hs2+a2)3          (5)

C = — -1,5^0 + ln3sT I Ap^--1 hs         10        T12^T где hs – глубина распространения пластической деформации;

e _T – деформация на пределе текучести [5].

Далее рассчитывали текущие значения энергии пластической деформации u_i для любой точки по глубине распространения пластической зоны при вдавливании вдоль оси z от 0 до h_s :

Объектом исследования служили стали 17ГС, 17ГС-У, 06Г2НАБ, 10Г2ФБ, 10Г2ФБ-У, 10ХГНМАЮ, применяющиеся для изготовления труб большого диаметра и корпусов атомных реакторов, свойства которых определяли в широком интервале температур. Механические испытания указанных сталей были выполнены в Институте проблем прочности НАН Украины [6]. Эксперименты по контактному деформированию проводили в Волгоградском государственном техническом университете [1]. Для исследования глубины распространения пластической зоны контактное деформирование проводили сферическим индентором диаметром D = 5 мм при нагрузках Р от 147 до 11 875 Н и температурах от 77 К до 293 К на приборах ТШ-2 (Бринелль) и ТК-2 (Роквелл).

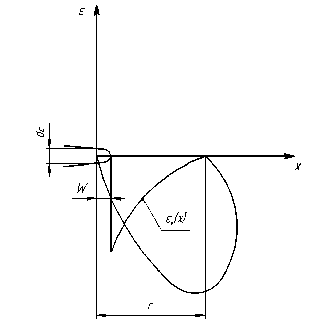
Рис. 1. Распределение деформации в малой пластической зоне перед фронтом трещины

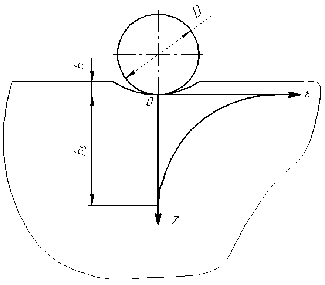
Рис. 2. Распределение деформации под остаточным отпечатком при внедрении сферы в плоскую поверхность упругопластического контртела

Сравнение значений r и h_s показало, что размер пластической зоны перед фронтом трещины более чувствителен к снижению температуры, чем при вдавливании индентора. Поэтому было предложено считать, что размеры пластических зон соответствуют друг другу при температуре 77 К нагрузке 150 Н, при температуре 213 К – 1 000 Н, при температуре 243 – 5 000 Н, при температуре 293 К– 11 800 Н.

Далее проводился расчет значений удельной энергии пластической деформации по глуби- не пластической зоны при вдавливании сферического индентора up. Было показано, что энергетические параметры пластических зон при вершине трещины gр и при вдавливании сферического индентора up пропорциональны (рис. 3).

Зависимость между вязкостью разрушения K _{I C} и u p описывается прямой линией (рис. 4), которую можно аппроксимировать уравнением (9):

К_IC = 514,01 u p – 27,785. (9)

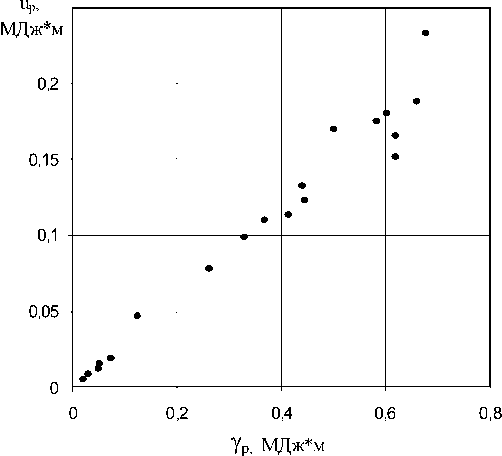
Рис. 3. Зависимость u_p и g _р

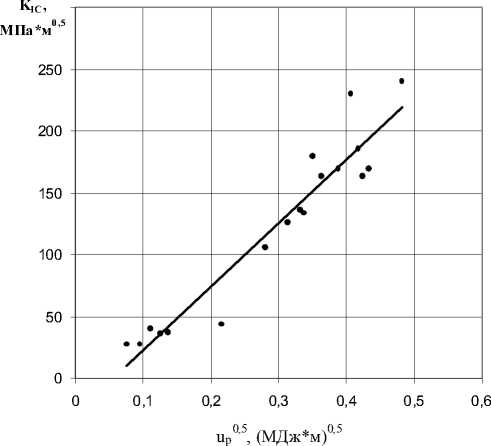
Рис. 4. Зависимость K _{I C} и u p

Таким образом, появляется возможность прогнозирования сопротивления хрупкому разрушению по результатам контактного деформирования материалов.