Оценка влияния неравномерности поверхности оптических кристаллических микрорезонаторов на их дисперсионные характеристики

Открытие методов генерации оптических частотных гребенок явилось одним важнейших прорывов в фотонике, позволивших создать высокоэффективный исследовательский инструмент, за создание которого его авторы Т. Хенш, Д. Холл и Р. Глаубер в 2005 году были удостоены Нобелевской премии по физике [1].

Оптические частотные гребенки (ОЧГ), представляющие собой набор узких эквидистантных спектральных линий, первоначально создавались с использованием громоздких установок на основе фемтосекундных лазеров с синхронизацией мод [2]. В последние годы были предложены методы генерации ОЧГ на основе сферических или дисковых оптических микрорезонаторов (ОМР) с модами «шепчущей галереи» (МШГ), обладающими высокой добротностью [3]. Эти устройства, которые в научной литературе также называют МШГ-резонаторами, стали объектом интенсивных исследований, проводимых в России и за рубежом [4–6].

Если ОМР изготовлен из оптически нелинейных материалов, то при его накачке от лазера с непрерывной волной и достаточной мощностью за счет эффекта Керра возникает так называемое четырехволновое смешение, в результате которого происходит перераспределение фотонов между модами и возникает ОЧГ [6]. ОЧГ, генерируемые с помощью нелинейных ОМР, в современной научной литературе называются «керровскими гребенками» или «микрогребенками» [7– 10].

ОМР обладают малыми размерами, высокой добротностью и стабильностью характеристик, являются дешевыми в изготовлении и легко интегрируются в оптические системы. На их основе создаются оптические измерительные приборы, обладающие рекордной чувствительностью [11 – 16]. Приборы для генерации ОЧГ на базе нелинейных ОМР уже представлены на рынке и могут в перспективе заменить сложные и дорогостоящие генераторы ОЧГ на основе фемтосекундных лазеров. Это позволит создавать различные типы недорогих миниатюрных оптических систем и измерительных приборов на основе ОЧГ, встроенных в волоконно-оптические линии, которые будут широко применяться в фотонике, спектроскопии, телекоммуникационных технологиях, навигационных системах, метрологии и т.д.

Известно, что малые (порядка нескольких нанометров) изменения геометрии ОМР кардинально влияют на его спектральные свойства [17], поэтому актуальной задачей производства приборов с ОЧГ на основе ОМР является разработка методов изготовления и расчета спектральных характеристик микрорезонаторов.

1.    Генерация частотной гребенки

Рассматриваемый генератор ОЧГ состоит из двух основных элементов – высокодобротного ОМР, изготовленного из оптически нелинейного материала, и системы связи в виде оптического волокна с перетяжкой или призмы (рис. 1).

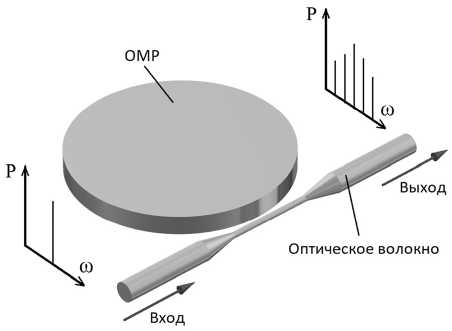
Рис. 1. Схема генератора ОЧГ на основе высокодобротного ОМР

Высокие достижимые добротности в МШГ микрорезонаторах понижают порог проявления нелинейных эффектов до величин менее единиц милливатт. При достаточной мощности накачки на основе эффекта Керра в МШГ-резонаторе могут возбуждаться ОЧГ в результате каскадного четырехволнового смешения [7].

Четырехволновое смешение – параметрическое преобразование частоты, в результате которого аннигилируют два фотона накачки и рождается пара фотонов: сигнальный с повышением частоты и холостой с понижением частоты. Вследствие закона сохранения энергии фотоны рождаются равноудаленными от частоты накачки. Если рожденная пара фотонов совпадает с собственными частотами микрорезонатора, то такой процесс происходит значительно эффективнее. Случай, когда рожденные фотоны, сигнальный и холостой, начинают сами участвовать в процессе параметрической генерации, называют каскадным четырехволновым смешением.

Если мощность лазера накачки превышает пороговый уровень, то частотная гребенка формируется благодаря каскадному процессу образования боковых спектральных линий, соответствующих взаимодействию всевозможных фотонов, удовлетворяющих условиям сохранения энергии и импульса. Спектральные линии, образующие гребенку, имеют эквидистантный частотный интервал, обычно лежащий в диапазоне 10÷ 1000 ГГц [7].

2.    Изготовление ОМР

Наиболее распространенными материалами для изготовления ОМР являются фторид кальция (CaF 2 ), фторид магния (MgF 2 ), нитрид кремния (Si 3 N 4 ), кристаллический кварц (SiO 2 ) и т.п., имеющие низкий коэффициент поглощения в оптическом диапазоне. Для снижения излучательных потерь при изготовлении ОМР добиваются величины остаточной шероховатости поверхности не более нескольких нанометров. Технология изготовления ОМР, в частности метод точечного алмазного точения с последующей асимптотической полировкой, позволяет достигать исключительно высокой добротности – около 10⁸ ÷ 10⁹ и подробно описан в статье [18].

Однако несмотря на отработанность технологии, в процессе производства возможно возникновение дефектов в виде неравномерности формы образующей. Под неравномерностью мы понимаем одиночные или периодически повторяющиеся кольцевые выемки на поверхности ОМР (рис. 2).

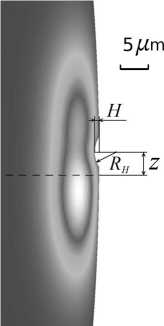
Рис. 2. Распространение моды в приповерхностном слое ОМР с неравномерностью образующей. R H – радиус неравномерности, H – глубина неравномерности, Z – смещение неравномерности относительно экваториальной плоскости ОМР (пунктирная линия)

Такие неравномерности распространяются по всему периметру микрорезонатора и обусловлены сполировыванием сколов, которые образовались в процессе алмазного точения ОМР. Кольцевые выемки небольшой глубины могут оставаться на поверхности ОМР даже после длительной полировки суспензиями с размером зерна меньше 0,5 мкм. Подобные дефекты могут вызывать изменение дисперсионных характеристик ОМР. Множество работ различных научных групп посвящено исследованию зависимости дисперсии от выбора материала, размеров и формы ОМР [19–24], однако вопрос влияния дефектов формы остается открытым.

Целью данной работы является численное моделирование влияния неравномерности формы образующей, возникающей на поверхности ОМР в результате изготовления, на дисперсионные характеристики и расщепление моды.

3.    Моделирование характеристик ОМР

ОМР обладают следующими основными дисперсионными характеристиками: частота основной моды f m , расстояние между соседними модами Δ f и суммарная дисперсия D Σ , характеризующая отклонение частот спектральных линий от эквидистантности.

Для расчета приведенных характеристик рассмотрим основные параметры, которыми можно описать ОМР. В качестве геометрической модели микрорезонатора использовался тороид, который определяется радиусом R и радиусом кривизны образующей r (рис. 3 б ).

* i ч L J

• а)                 б)                     в)

Рис. 3. (a) Фотография ОМР на латунной подставке; (б)

геометрическая модель кристаллического ОМР; (в) микрофотография неравномерности на выступе ОМР, полученная с применением шестилепестковой ирисовой диафрагмы

Тороидальный микрорезонатор содержит большой набор собственных мод, однако в формировании ОЧГ участвуют моды, однозначно определяемые номером моды m, который можно интерпретировать как число длин волн на один полный оборот внутри резонатора. Собственные резонансные частоты ОМР fm определяются выражением fm - mc / (2nRneff (Xm )),                            (1)

где m – номер моды; c – скорость света в вакууме; λ m – длина волны моды; R – радиус ОМР; n eff (λ) – эффективный показатель преломления материала.

Расстояние между собственными модами ОМР (англ. Free Spectral Range , FSR ) или область свободной дисперсии микрорезонатора определяется выражением

FSR - c /(2 л Rn g ( X m )),                           (2)

где ng (λ) – групповой показатель преломления материала, ng (X)- neff (X) - Xdnef (X) / dX .                    (3)

Генерация ОЧГ в микрорезонаторе с МШГ может быть описана уравнением Луджиато–Лефевера [25], различные решения которого показывают возможность получения различных сигналов, например роллов Тьюринга, тёмных и светлых солитонов, плати-конов, хаоса. Тип сгенерированной ОЧГ задается тремя параметрами: мощностью накачки, отстройкой лазера и дисперсией ОМР [5]. Для разработки средств измерений на базе ОЧГ удобнее всего использовать солитонные гребенки, генерация которых возможна в случае аномальной дисперсии при отстройках частоты в красную область и достаточной мощности лазера накачки [5].

Расчет характеристик ОМР может быть выполнен с помощью коммерчески доступного программного обеспечения, например, COMSOL Multiphysics , используемого для решения физических и инженерных задач методом конечных элементов (МКЭ) [26]. МКЭ является одним из наиболее распространенных в настоящее время численных методов решения широкого круга задач и моделирования физических процессов. Сутью МКЭ является представление объекта моделирования совокупностью элементов конечно малого размера, связанных между собой в узлах, и решение системы уравнений для расчета интересующих параметров в каждом узле с дальнейшей аппроксимацией.

МКЭ является удобным инструментом, позволяющим провести расчеты основных характеристик ОМР, близких по своим параметрам к тем, которые в настоящее время реально создаются и исследуются с целью разработки перспективных средств измерений [27, 28]. С помощью МКЭ можно произвести расчет резонансных частот, моделирование распределения модового поля, рассчитать эффективный объем моды, эффективный показатель преломления, излучательную добротность ОМР и т.д.

Для более точного расчета резонансных частот следует учитывать, что показатель преломления материала зависит от длины волны согласно уравнению Селлмейера [29]:

n ² ( X ) - 1 + S ( Ai X ²)/ ( X ²- B i ²) ,                     (4)

где А i , В i – экспериментально определенные коэффициенты Селлмейера для материала ОМР. Поэтому после определения резонансной частоты необходимо в процессе нескольких итераций уточнять значение n (λ) согласно уравнению (4) и заново пересчитывать параметры модели.

Дисперсия электромагнитных волн является важнейшим фактором, влияющим на характеристики ОЧГ на основе ОМР. Из-за дисперсии моды одного порядка не являются строго эквидистантными. Частота моды ω μ может быть представлена в виде ряда Тейлора относительно основной частоты ω 0 :

Юц - too + Дц + D2ц2 /2!+ DзЦ3 /3!+ D^4 /4!+ — - (5) — too + D1Ц+D^, где µ= m – m0 – относительный номер моды, отсчитываемый от моды накачки μ =0;

• D 1 – область свободной дисперсии ( FSR );

• D 2 – коэффициент дисперсии второго порядка;

• D 3 , D 4 ,… – коэффициенты дисперсии высших порядков;

D Σ – суммарная дисперсия, характеризующая отклонение спектральной линии от эквидистантности.

Как правило, D 2 >>  D 3 >>  D 4 …, при этом отрицательное значение D 2 характеризует нормальную дисперсию, а положительное – аномальную. Наличие близкой к нулю аномальной дисперсии является необходимым условием генерации солитонной гребенки, однако большая по абсолютной величине дисперсия ограничивает ее ширину.

Отметим, что при моделировании необходимо учитывать как дисперсию материала, так и геометрическую дисперсию, обусловленную размерами и формой ОМР. Геометрическая дисперсия связана с тем, что различные моды проходят разные оптические пути внутри ОМР, что также приводит к их неравномерному смещению. Важным условием правильности расчёта является выбор аппроксимирующей функции для материальной дисперсии. Выбранная функция должна быть дифференцируема не меньшее число раз, чем определяемый порядок дисперсии. Так, например, использование дискретных данных для n eff (λ) с интерполяцией сплайном может приводить к случайному результату для D 2 .

Для расчета изменения расстояния между модами из-за дисперсии с помощью МКЭ можно определить эффективный показатель преломления neff на различных частотах, а затем определить эффективный номер моды meff с длиной волны λ согласно выражению mef- 2kRnff (X)/ X.(6)

При этом реальные частоты мод соответствуют целочисленным значениям m eff . Величину D 1 (ω) можно рассчитать исходя из соотношения

D1(®) - d® / dmf - 2uFSR.(7)

Отклонение частот спектральных составляющих от эквидистантности (суммарная дисперсия) определяется как

D -го,— ®o- Дц.(8)

Для подтверждения корректности метода расчета дисперсии с помощью МКЭ было проведено моделирование ОМР из MgF2 с радиусом R = 1,612 мм (FSR ~ 21,6 ГГц) в воздушной среде. Показатель преломления материала задавался в виде функции n - sqrt(1 + 0,48755108 -X2 / (X2 - 0,043384082) + +0,39875031 -X2 / (X2 - 0,094614422) +          (9)

+ 2,3120353 -X ² / ( X ² -23,793604 2 ) ).

Коэффициенты в выражении (9) определены для соответствующего материала с помощью Refractive index database [30].

При построении геометрической модели ОМР использовался двумерный осесимметричный режим в COMSOL Multiphysics. Следует отметить, что в осесимметричной геометрии расчет эффективного показателя преломления встроенным методом «Анализ мод» (предназначенным для прямых волноводов) выдает комплексные значения R∙neff вместо значения neff, что нужно учитывать при дальнейших расчетах.

Для анализа использовался интерфейс «Электромагнитные волны. Частотная область» раздела «Волновая оптика», который поддерживает режим «Анализ мод» и позволяет корректно решать волновое уравнение для гармонического электромагнитного поля при условии, что максимальный размер элемента расчетной сетки ограничен долями (не более 1/8) от длины волны.

Сравнение результатов моделирования с данными экспериментальных исследований, полученных в работе [19], приведены на рис. 4. Сильное отклонение экспериментальных данных около частот 194,5 и 195,5 ТГц вызвано явлением пересечения между различными семействами мод [31]. Как можно убедиться, расчет дисперсии с помощью МКЭ и определения эффективного номера моды показывает близкое совпадение с экспериментальными данными.

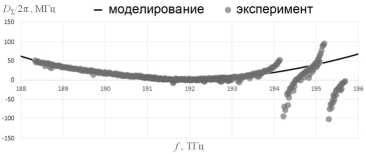
Рис. 4. Сравнение результатов расчета суммарной дисперсии ОМР из MgF 2 с экспериментальными данными, полученными в работе [19]

Однако на значение D Σ влияют не только выбор материала и геометрических размеров ОМР, но и другие параметры, в частности неравномерность образующей в области распространения моды. На рис. 5 приведены расчеты зависимости суммарной дисперсии ОМР из CaF 2 с параметрами R = 1600 мкм, r = 100 мкм при наличии кольцевого углубления глубиной H и смещенной от экватора резонатора на величину Z =0. Предполагалось, что выемка имеет круглый профиль с радиусом R Н =5 мкм и параллельна экватору ОМР. Расчёт выполнен для частоты лазера накачки 192 ТГц (1550 нм).

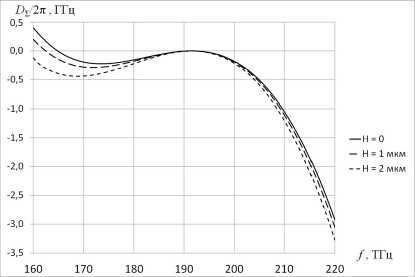
Рис. 5. Расчет зависимости суммарной дисперсии от частоты для тороидального ОМР из СаF 2 с R = 1600 мкм, r = 100 мкм и различными значениями неравномерности образующей H при R Н = 5 мкм, Z = 0

Результаты исследований показали: наличие выемки вызывает изменение D Σ , что, в свою очередь, будет оказывать влияние на параметры генерируемой ОЧГ, особенно в области низких частот. В частности, наличие неравномерности смещает область появления дисперсионной волны [32, 33], что может помешать присоединению её спектра к спектру основной гребёнки. Подобное влияние также дает возможность корректировать значение дисперсии с помощью микропрофилирования – намеренного нанесения выемки на поверхность ОМР.

Особенно интересным является исследование возможности управления с помощью микропрофилирования коэффициентом дисперсии второго порядка D 2 , во многом определяющим как возможность генерации, так и параметры генерируемой ОЧГ.

Рассмотрим подробней дисперсионные характеристики подобного микрорезонатора из СаF 2 . Результаты расчета изменения коэффициента D 2 = d ²ω / dm eff ² для различных параметров приведены на рис. 6. Из рис. 6 видно, что подбором параметров R H , H, и Z можно добиться изменения показателя дисперсии D 2 более чем на 30%. Неочевидным является результат, когда максимум функции D 2 ( Z ) находится не в положении Z =0, при котором наблюдается сильное расщепление формы оптической моды (рис. 9 a ), а в положении, отстроенном от него на некую величину по Z (на рис. 6 от 2 до 4 мкм). Это может объясняться тем, что в случае Z = 0 в резонаторе образуется два одинаковых связанных резонатора, и в такой симметричной системе геометрическая дисперсия не оказывает сильного влияния, что, однако, изменяется при увеличении глубины выреза H (рис. 6 для H = 1,5 мкм). В то же время при Z ≠ 0 мода расщепляется несимметрично и возникает сильная геометрическая дисперсия. Однако увеличение Z до величин более 10 мкм приводит к тому, что вырез расположится вне области распространения света в резонаторе и не окажет значительного воздействия на дисперсионные характеристики.

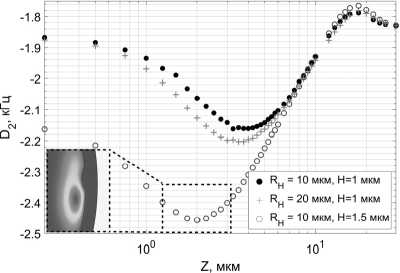
Рис. 6. Рассчитанная величина дисперсии D 2 микрорезонатора для различных параметров R H , H, и Z. На вставке показано характерное распределение поля в отмеченной пунктиром области

Зависимость изменения дисперсионных характеристик от H представлена на рис. 7. На ней видно, что при достижении определенного порога по глубине выемки дальнейшее ее увеличение не приводит к значительному росту D2, так как при этом не возникает расщепления формы моды и поле сосредотачивается в области между выемкой и основной образующей резонатора (рис. 9).

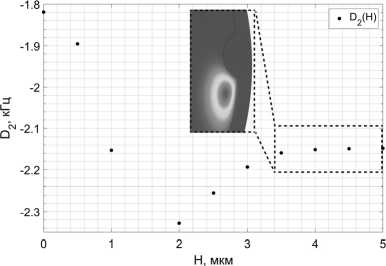
Рис. 7. Рассчитанная величина дисперсии D 2 для различных параметров H при Z = 3,5 мкм. На вставке показано характерное распределение поля в отмеченной пунктиром области

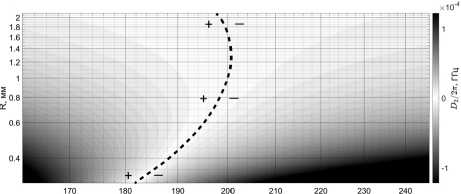
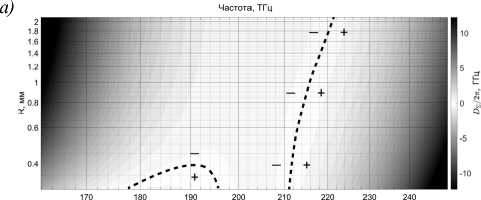
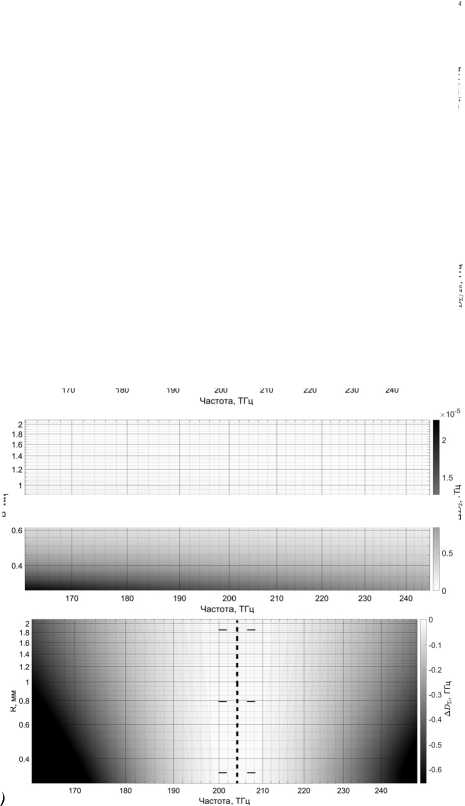
Рассмотрим теперь, как рассматриваемый эффект проявляется при различных соотношениях геометрических размеров резонатора и длины волны, а также покажем, что эффект проявляется по-разному в зависимости от длины волны. Был выполнен расчёт для радиусов резонатора от 0,3 до 2,3 мм и для частот от 161 ТГц до 245 ТГц. На рис. 8 а , б показан расчёт D 2 и D Σ для микрорезонатора при отсутствии неравномерности. На рис. 8 в , г показаны величины изменения D 2 и D Σ при добавлении неравномерности. Видно, что в зависимости от длины волны величина эффекта заметно разнится. Из рисунков понятно, что добавление неравномерности смещает положения нулевых значений D 2 и D Σ .

Стоит отметить, что наличие микропрофилирования может приводить к расщеплению формы моды, этот эффект особо чувствителен к значению глубины неравномерности H. При увеличении глубины неравномерности до 1,5 мкм и более происходит расщепление формы моды на 2 части (рис. 9).

Наличие нескольких выемок в области распространения моды также приводит к её существенному искажению либо расщеплению формы (рис. 10).

Таким образом, результаты исследования свидетельствуют о зависимости дисперсионных характеристик ОМР и формы моды от параметров неравномерности образующей, что подтверждает важность контроля состояния поверхности в области распространения моды при изготовлении микрорезонаторов, а также дает возможность корректировать значение дисперсии с помощью микропрофилирования.

Заключение

В работе продемонстрирован метод расчета суммарной дисперсии кристаллических ОМР, применяемых для создания так называемых «керровских» гре- бенок, с помощью МКЭ, а также исследовано влияние неравномерности образующей на величину дисперсионных характеристик на примере ОМР из CaF2. Авторами показано, что наличие на поверхности неравномерности может приводить к эффекту расщепления формы моды в микрорезонаторах, отмечается важность учёта этого эффекта при конструировании устройств на основе оптических ОМР. Выявлено, что значение дисперсии ОМР можно корректировать с

помощью нанесения выемок на его поверхность, однако микропрофилирование может негативно влиять на ширину ОЧГ и положение дисперсионной волны. Показано, что данный эффект особо зависит от положения и значения глубины неравномерности.

б)

в)

• г)

Рис. 8. a), б) – Расчёт коэффициента дисперсии второго порядка D 2 микрорезонатора с r = 400 мкм в отсутствие неравномерности для различных длин волн и геометрических размеров. Пунктиром показана область, в которой наблюдаются нулевые значения дисперсии D 2 ; в), г) расчёт изменения дисперсии микрорезонатора при добавлении неравномерности с H = 3,0 мкм, Z = 2 мкм и R h = 100 мкм

Российским научным фондом (проект № 21-72-00132). Данилин А.Н. является стипендиатом Фонда развития теоретической физики и математики «БАЗИС».

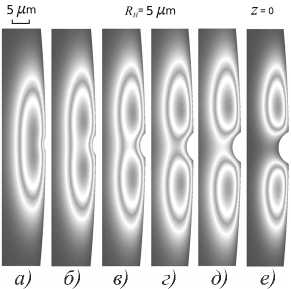
Рис. 9. Расщепление формы моды ОМР из СаF 2 с R = 1600 мкм, r = 100 мкм при увеличении глубины неравномерности образующей H при R Н = 5 мкм, Z = 0, λ ~ 1550 нм. (a) H = 0,5 мкм; (б) H = 1,0 мкм; (в) H = 1,5 мкм;

(г) H = 2,0 мкм; (д) H = 2,5 мкм; (е) H = 3,0 мкм

Рис. 10. Расщепление формы моды ОМР из СаF 2 с R = 1600 мкм, r = 100 мкм при увеличении расстояния между неравномерностями образующей c H = 1,5 мкм, R Н = 5 мкм, λ ~ 1550 нм. (а) Z = ± 5 мкм; (б) Z = ± 6 мкм; (в) Z = ± 7 мкм; (г) Z = ± 8 мкм; (д) Z = ± 9 мкм; (е) Z = ± 10 мкм