ОЦЕНКА ВЛИЯНИЯ ОБЪЕМНОГО ЗАРЯДА НА РАЗРЕШЕНИЕ ИОН-ДРЕЙФОВОГО СПЕКТРОМЕТРА

В настоящее время спектрометрия ионной подвижности все чаще используется в ряде приложений [1]. Принцип работы ион-дрейфового спектрометра (рис. 1) основан на том, что скорости дрейфа разных ионов в электростатическом поле в газе различаются. Давление газа, заполняющего дрейфовую камеру, атмосферное. В результате дрейфа ионы разделяются и последовательно детектируются приемником. В качестве источника ионизации обычно используется либо источник β-частиц (63Ni), либо коронный разряд. Коронный разряд часто применяется в ион-дрейфовых спектрометрах (ИДС), когда требуется источник нерадиоактивных ионов с высокими ионными токами. Как правило, за коронным разрядом следует область реакции, в которой из ионов реагента образуются ионы аналита. Короткий ионный импульс формируется затвором, который располагается между источником ионов и коллектором.

Рис. 1. Схема ион-дрейфового спектрометра с затвором Бредбери – Нильсена

В сочетании с масс-спектрометрией cпектро-метрия ионной подвижности является мощным аналитическим инструментом для разделения сложных образцов и исследования молекулярных структур. Поэтому крайне важной задачей становится повышение разрешающей способности и чувствительности ИДС. Увеличение ионных токов должно способствовать повышению чувствительности и эффективной регистрации сигналов. Однако с увеличением ионной плотности начинают проявляться кулоновские эффекты, которые увеличивают пространственную дисперсию ионных пучков, находящихся в дрейфовой трубке, и приводят к снижению разрешающей способности ИДС. Таким образом, кулоновские силы объемного заряда вызывают дополнительное по сравнению с диффузионным уширение ионного сигнала. Кроме того, наряду с увеличенной пространственной дисперсией кулоновское отталкивание также оказывает влияние на среднюю скорость дрейфа ионов внутри пакета, создавая систематические ошибки в измерениях подвижности ионов. Два пакета ионов, обладающих близкой подвижностью ионов, взаимодействуют таким образом, что в среднем компонент с меньшей подвижностью движется медленнее, и наоборот.

Минимизация кулоновских эффектов важна для достижения оптимального сочетания высокого динамического диапазона и высокой разрешающей способности ИДС. Оценка величины плотности тока, выше которой начинает сказываться влияние объемного заряда, дана в работе [2]. За критерий взята такая концентрация заряженных частиц, при которой в рассматриваемых условиях движение ионов в собственном поле превосходит скорость перемещения за счет диффузии. Критическая величина плотности тока для характерных условий работы ИДС оценивается как 10–6 А/м2. В работе [3] было показано, что роль объемного заряда становится существенной при начальных плотностях ионов, превышающих 106 cм–3. Эффект объемного заряда в ИДС рассматривался также в работах [4, 5]. В работе [6] потери ионов и разрешающая способность систем в зависимости от плотности входного заряда и соотношения сторон дрейфовой трубки (длина / диаметр) определялись посредством моделирования в программе SIMION [7].

В данной работе представлена аналитическая модель, описывающая динамику ионного облака под действием объемного заряда при движении в ион-дрейфовом спектрометре от источника ионов до коллектора. Получены выражения, которые позволяют оценить роль объемного заряда в увеличении ионных потерь и уменьшении разрешающей способности прибора.

МОДЕЛЬ ДВИЖЕНИЯ ИОННОГО ОБЛАКА ПОД ДЕЙСТВИЕМ ОБЪЕМНОГО ЗАРЯДА

Построим модель, описывающую динамику ионного облака под действием собственного объемного заряда. Рассмотрим для определенности равномерное распределение заряженных частиц внутри длинного цилиндра.

Напряженность электрического поля заряженного диска вдоль оси ξ , перпендикулярной его плоскости, изменяется согласно

E ( ^ =

σ

² ' ^S 0

1 +

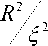
где R — радиус диска, σ — поверхностная плотность зарядов, ε 0 — диэлектрическая проницаемость. Поверхностная плотность зарядов выражается через объемную плотность, как о = р d e . Для определения напряженности электрического поля заряженного цилиндра длиной L проинтегрируем по x выражение (1) относительно точки, расположенной на его оси на расстоянии x от торца. В результате получим следующее выражение:

E ( x ) = ( L - J ( x + L )² + R ² + V x ² + R ² ) . (2) ² • ^S gV ’

Напряженность электрического поля снаружи заряженного длинного цилиндра имеет, как известно, вид:

E ( r ) = ^ R ², ² • ^S 0 r

где r — радиус ( r > R ), расстояние от оси до точки наблюдения.

Рассмотрим теперь распределение N ионов в цилиндре с начальной длиной L 0 и радиусом R 0 . Предполагаем равномерное распределение ионов по объему. Соответственно концентрация ионов в рассматриваемом цилиндрическом объеме будет

равна

NV, =

N πR 0 ² L 0

и объемную плотность тогда

можно представить как р = qNV_o

qN πR 0 ² L 0

. Движе-

ние заряженной частицы в газе под действием электрического поля характеризуется коэффициентом подвижности. Скорость разлета ионов на границах области будет определяться коэффициентом подвижности K и соответствующей на-

пряженностью электрического поля, определяемо-

го пространственным распределением ионов: и = KE . Полагая цилиндр достаточно длинным,

чтобы пренебречь особенностями динамики разлета ионного облака на стыке осевой и радиальной поверхностей, получим, что начальная радиальная скорость движения границы будет равна qNV R0

u_R = K ---0—,  а продольная скорость —

2 ε ₀

d R _ K_qN __ 1

d t    2 πε ₀         2 KqNt

RL, 1 + у πε 0 R 0 L ² 0

(6б)

Эти уравнения легко интегрируются, их решения имеют вид:

qN_{V              2    2}

u_L = K ---- ( L ₀ + R ₀ - J L ₀ + R ₀). Изменение кон-2 ε ₀

L ( t ) _ L 0

центрации ионов вследствие разлета облака цилиндрической формы определяется как

1 + 4 R 0 L 0

Л Г"

1 +

V

KqNt πε ₀ R ₀ ² L ₀

^

^- 1 ^

N v =

N n (R 0 + URt )2( L0 + 2uLt)

N πR ² L ^,

L

^{R (} t ) ^{_ R} 0f ⁺ R "W

< Г"

1 +

2 KqNt πε ₀ R ₀ L ² ₀

—

^ 1 J .

поскольку R = R ₀ + u_Rt , L = L ₀ + 2 u_Lt .

Соответственно изменение размеров облака во времени будет описываться системой дифференциальных уравнений

d L qNN ( L + R — V L ² + R ²)     qN 1

_ K2~ K, dt    πε0       R2L          πε0 RL при (L > R); (4а)

d R _ K qN 1

d t     2 πε ₀ RL ^{.                              (4б)}

Независимое рассмотрение только радиального (длина L 0 не меняется) и продольного (радиус R 0 не меняется) разлетов дает решения:

L ( t ) _ L 0

2 KqNt πε ₀ L ² ₀ R ₀

Таким образом, уравнения (7) и (8) описывают изменение геометрических размеров ионного облака цилиндрической формы во времени вследствие их взаимного кулоновского расталкивания. 1

Видно, что при больших временах L ( t ) ~ t ⁴

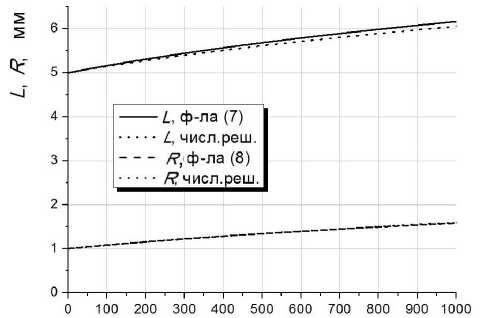
и R ( t ) ~ t ⁴ , а при малом количестве ионов геометрические размеры облака практически не меняются. В качестве примера рассмотрим начальное цилиндрическое ионное облако длиной L ₀ = = 0.5 см и радиусом R 0 = 0.1 см, число однозарядных ионов в нем N = 10⁷, коэффициент подвижности ионов K = 1.5 см²/(В·с). На рис. 2 представлены зависимости от времени длины и радиуса ионного облака, согласно (7) и (8), а также результаты численного решения системы (4) с помощью FORTRAN-программы решения жесткой системы дифференциальных уравнений RADAU5 [8] без поочередного разделения движения на продольную и поперечную компоненты и без упрощающего

1 +

R ( t ) _ R 0

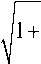
KqNt πε ₀ R ₀ ² L ₀

Подставим эти решения обратно в соответствующие уравнения системы (4). Т.е. теперь при радиальном разлете учитывается изменение продольных размеров облака, а при осевом (продольном) — радиальных размеров. Таким образом, получим запись системы (4): два дифференциальных уравнения, описывающие радиальный и продольный разлет протяженного ионного облака цилиндрической формы с начальной длиной L 0 и радиусом R 0 :

t, MKC

Рис. 2. Зависимости от времени длины L и радиуса R ионного облака согласно выражениям (7) и (8), а также результаты численного решения системы при L 0 = 0.5 см, R 0 = 0.1 см, N = 10⁷, K = 1.5 см²/(В·с)

d L _ K_qN __ 1

d t     2 πε ₀           KqNt ^,

LR, 1 +—

⁰ πε 0 R 0 ² L 0

(6а)

предположения, что длина облака существенно больше его радиуса. Видно, что зависимости хорошо согласуются между собой, подтверждая тем самым адекватность аналитической модели.

Изменение во времени плотности заряда происходит также за счет диффузии. В работе [2] были рассмотрены условия, при которых движение ионов в собственном поле начинает превосходить скорость перемещения за счет диффузии. Критическая величина плотности тока для характерных условий работы ион-дрейфовых спектрометров оценивается как 10–6 А/м2. Для наших условий, приведенных выше, это означает, что критическая плотность заряда составит 106 см–3. Таким образом, рассматривая плотность ионов заметно выше критической, мы предполагаем, что вклад диффузии по сравнению с объемным зарядом мал.

ВЛИЯНИЕ ОБЪЕМНОГО ЗАРЯДА

НА ПРОПУСКАНИЕ ИОННОГО ТРАКТА

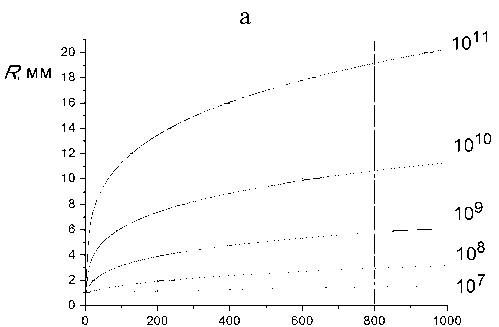
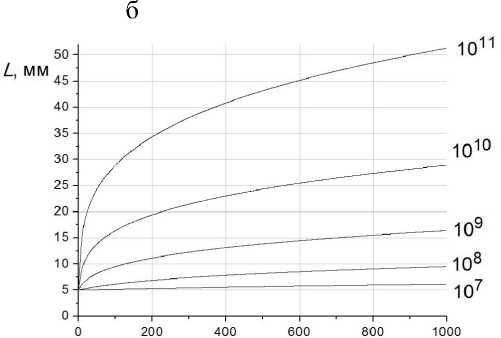
Уравнения (7) и (8) дают возможность оценить изменение геометрических размеров ионного облака цилиндрической формы во времени вследствие их взаимного кулоновского расталкивания. Рассмотрим эволюцию ионного облака длиной 0.5 см, радиусом 0.1 см, с K = 1.5 см²/(В·с). Облако движется по зоне протекания реакций непосредственно от источника к затвору, который формирует короткий ионный импульс. На рис. 3 показаны зависимости от времени радиуса R (рис. 3, a) и продольных размеров L (рис. 3, б) ионного облака при разном количестве ионов ( N = 10⁷–10¹¹), находящихся в начальном цилиндрическом объеме (0.016 см³). Влияние объемного заряда начинает сказываться уже при плотностях ионов, превышающих 10⁶ cм^–3, что согласуется с результатами работы [3]. Так, при плотности 6.4·10⁶ см^–3 ( N = = 10⁵) через 1 мс разлета радиус ионного облака цилиндрической формы увеличивается на 1%, при плотности, на порядок большей, — почти на 10%.

Исходя из начальных параметров ионного пучка, возможно оценить потери ионов и плотность ионного тока по длине дрейфовой трубки. То есть, задавая радиус трубки и напряженность электрического поля дрейфа, возможно определить поперечные размеры пучка и, соответственно, расстояние по длине трубки, начиная с которого будет наблюдаться потеря ионов вследствие их взаимного расталкивания и выноса за пределы дрейфовой области. Так, в случае уже рассмотренного примера, при радиусе дрейфовой трубки 15 мм и напряженности электрического поля дрейфа 500 В/см получим, что в зависимости от числа ионов в начальном объеме 109 и 1010 потери ионов начнутся соответственно на расстояниях 2.25 и 22.5 см

t, мкс

t, мкс

Рис. 3. Зависимости, согласно (8) и (7), от времени радиуса R (a) и продольных размеров L (б) ионного облака, разлетающегося под действием кулоновского расталкивания разного количества ионов (10⁷–10¹¹), находящихся в начальном цилиндрическом объеме (0.016 см³)

от начального. Причем для бóльших величин K потери будут наступать раньше.

ФОРМИРОВАНИЕ ИОННОГО ИМПУЛЬСА ЗАТВОРОМ БРЕДБЕРИ – НИЛЬСЕНА С УЧЕТОМ ОБЪЕМНОГО ЗАРЯДА

Рассмотрим формирование ионного импульса затвором Бредбери – Нильсена [9, 10]. Затвор Бредбери – Нильсена является одним из важных элементов ион-дрейфового спектрометра. Он представляет собой последовательность параллельных электропроводящих нитей, расположенных в одной плоскости, причем разность потенциалов между соседними нитями может меняться во времени. Потенциал одной последовательности нитей (через одну) равен потенциалу поля дрейфа в плоскости расположения затвора, а потенциал другой последовательности нитей ниже, что соответствует закрытому состоянию затвора, поскольку ионы теряются именно на этих нитях. При выравнивании потенциалов нитей затвор открывается, и образующийся ионный импульс попадает в область дрейфа и далее на коллектор.

Предположим, что скорость движения ионов во внешнем поле заметно превышает скорость движения, обусловленную собственным полем ионного пучка. Тогда время, затрачиваемое ионами при дрейфе в области ионизации от источника до затвора, определится, как

ДИНАМИКА ДРЕЙФА ИОННЫХ ПУЧКОВ И РАЗРЕШЕНИЕ ИОН-ДРЕЙФОВОГО СПЕКТРОМЕТРА

Для описания динамики ионного облака в дрейфовой области используем систему уравнений (4). В этом случае начальная длина ионного облака цилиндрической формы будет равна L d 0 = t g KE d , а начальный радиус R g . В выражениях (7), (8) N означает число ионов в облаке. Очевидно, что

в предположении равномерного распределения ионов внутри объема и того, что длина прошедшего облака не превышает длину исходного, число ионов, прошедших сквозь открытый затвор в об-

t =

Л ,

KEi

ласть дрейфа, будет равно N d = N

t g KE i L ( t i ) ^,

где L ( t i ) —

где Λ i — расстояние от ионного источника до затвора. Радиус ионного облака в плоскости затвора будет определяться поперечным уширением при движении ионного пучка в области ионизации, согласно (8), где t нужно заменить на t i , обозначим его R g :

продольный размер ионного облака (7) на момент его подхода к затвору (9) при E i ≈ E d . Поскольку длина формируемого затвором ионного импульса

оказывается меньше его поперечных размеров ( L d 0 = t g KE d <  R g ), то уравнение (4a) примет следующий вид:

R g

= R о

1 + L-

N   R о IV

Г

. 1+

2 qN Л i πε 0 R 0 L ² 0 E i

—

^

1}

dL qqN ( L + R — V L + R ²)   qqN 1

--= K--5--------~ K--7,   /114

d t     πε ₀         R ² L            πε ₀ R ²    (11)

при ( L <  R ).

При открытии затвора Бредбери – Нильсена потенциалы соседних нитей выравниваются на промежуток времени t g , и ионы проходят в дрейфовую область. Проходя сквозь открытый затвор, часть ионов теряется при столкновениях с нитями. Формально эти потери можно оценить через отношение задействованной поперечной площади всех нитей к площади поперечного сечения пришедшего ионного пучка. В результате на входе в дрейфовую область ионное облако имеет пространственную структуру, отвечающую "теням" от нитей. Пренебрежем этим для простоты и будем считать, что прошедшие ионы формируют ионное облако цилиндрической формы радиусом R g и длиной t g KE d , где E d — напряженность электрического поля в области дрейфа, поскольку по истечении временнóго интервала t_g потенциалы одной из последовательностей нитей затвора возвращаются в исходное состояние и затвор закрывается: далее ионы, не успевшие пройти в дрейфовую область, теряются на нитях с низким потенциалом. Следует отметить, что поскольку разные группы ионов имеют разные значения коэффициента подвижности, то и продольные размеры ионных облаков будут различны. При этом начальные радиусы ионных облаков R g от значений коэффициента подвижности не зависят.

Повторяя процедуру для этого случая, найдем, что изменения длины и радиуса ионного облака в зоне дрейфа будут описываться соответственно следующими выражениями:

Г     Г

L d ( t ) = L d о 1 + ln 1 +

I     V

R d ( t ) = R g

KqN_dt πε ₀ R_g ² L_d

,

1      1 KqN.t

1 + ln 1 + —4 .d n^R2,L,ln .

На рис. 4. представлены, согласно (12) и (13), зависимости от времени радиуса R (рис. 4, a) и продольных размеров L (рис. 4, б) ионного импульса, сформированного затвором, с учетом кулоновского расталкивания для разного начального количества ионов (10⁵–10¹¹), находящихся в исходном цилиндрическом объеме (0.016 см³ — цилиндр длиной 0.5 см, радиусом 0.1 см) в области ионообразования. Коэффициент подвижности ионов принимался равным K = 1.5 см²/(В·с), длина области ионообразования L i = 3 см, напряженности полей E i = E d = 500 В/см, длительность открытия затвора t g = 100 мкс. Видно, что влияние объемного заряда начинает заметно сказываться с N = 10⁷,

соответствующая плотность ионов в ионном им-

пульсе, 9.6·105 см

сформированном

затвором, равна

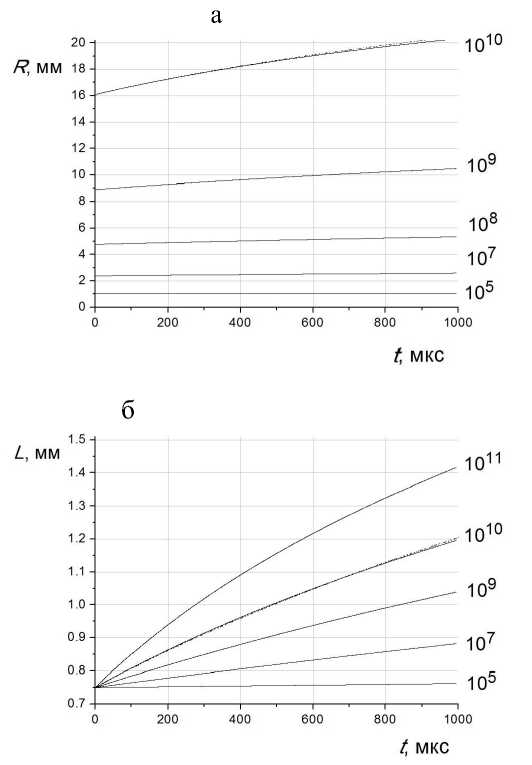
Рис. 4. Зависимости, согласно (13) и (12), от времени радиуса R (a) и продольных размеров L (б) ионного импульса, сформированного затвором, с учетом кулоновского расталкивания для разного начального количества ионов ( N = 10⁷–10¹¹), находящихся в исходном цилиндрическом объеме (0.016 см³) в области ионооб-разования. Для N = 10¹⁰ приведены кривые численного решения, которые практически совпадают с аналитическими

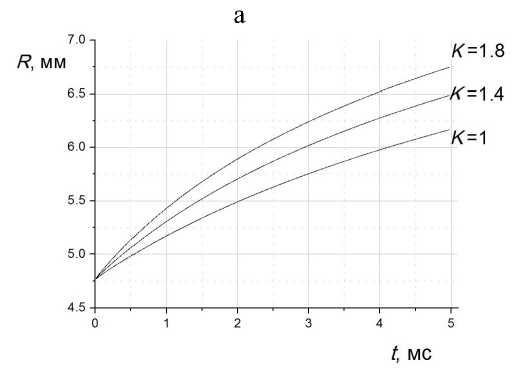
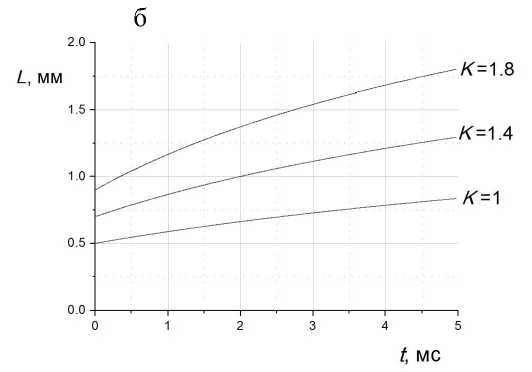
Рис. 5. Зависимости от времени радиуса R (a) и продольных размеров L (б) ионного импульса, сформированного затвором, с учетом кулоновского расталкивания для разных величин коэффициента подвижности — K = 1, 1.4, 1.8 см²/(В·с). Число ионов, находящихся в начальном цилиндрическом объеме (0.016 см³) в области ионообразования, составляет 10⁸

Также на рис. 4 для N = 10¹⁰ приведены зависимости, полученные посредством численного решения исходной системы уравнений с помощью программы решения жесткой системы дифференциальных уравнений RADAU5 [8]. Видно, что кривые практически совпадают.

Ширина прошедшего ионного импульса зависит от величины коэффициента подвижности определенного иона. Чем больше коэффициент подвижности, тем шире прошедший импульс независимо от плотности заряда. При этом учет объемного заряда приводит к дополнительному уширению в зависимости от величины коэффициента подвижности, согласно (12). На рис. 5 представлены зависимости от времени радиуса R (рис. 5, a) и продольных размеров L (рис. 5, б) ионного им- пульса, сформированного затвором с учетом кулоновского расталкивания для разных значений коэффициента подвижности (K = 1, 1.4, 1.8 см2/(В·с)). Число ионов, находящихся в начальном цилиндрическом объеме (0.016 см3) в области ионообра-зования, составляет 108. По-прежнему длина области ионообразования Li = 3 см, напряженности полей Ei = Ed = 500 В/см, длительность открытия затвора tg = 100 мкс. Очевидно, что чем больше значение коэффициента подвижности, тем сильнее происходит уширение ионного импульса. Причем плотности ионов в прошедших импульсах различаются: 3.8·106 см–3 (K = 1 см2/(В·с)), 5.33·106 см–3 (K = 1.4 см2/(В·с)), 6.85·106 см–3 (K = 1.8 см2/(В·с)).

В поле дрейфа ионный импульс движется как целое со скоростью KE d . Соответственно положение импульса со временем с учетом уширения

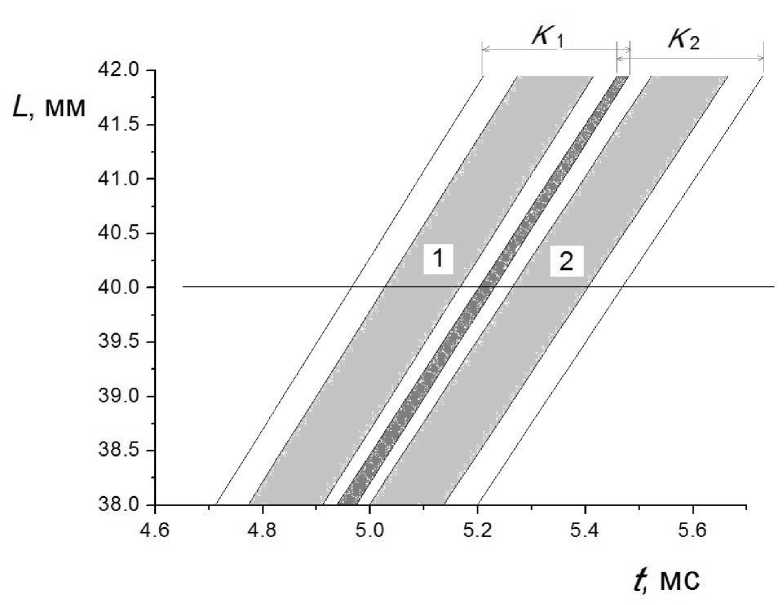
Рис. 6. Динамика изменения ширины ионных импульсов и их взаимного расположения при разных значениях коэффициентов подвижности ( K 1 = 1.5 и K 2 = 1.57 см²/(В·с)) с учетом влияния объемного заряда ионов внутри импульса (при N = 10⁶ — полосы (1), (2); при N = 10¹⁰ — уширившиеся полосы со взаимным пересечением)

за счет объемного заряда можно представить следующим образом. Для определения границ ионного импульса будем откладывать в обе стороны от положения его центра с продольной координатой, определяемой как tKEd, где t — время, отсчитываемое от начала движения импульса в дрейфовой области, половину ширины, определяемой выражением (12). Таким образом для разных сортов ионов, отличающихся коэффициентом подвижности, можно оценить их разрешение при заданных параметрах ИДС с учетом влияния объемного заряда. Например, на рис. 6 показана динамика изменения ширин ионных импульсов и их взаимного расположения для разных значений коэффициентов подвижности (K1 = 1.5 и K2 = 1.57 см2/(В·с)) с учетом влияния объемного заряда ионов внутри импульса (N = 106 и 1010), кулоновским взаимодействием между самими импульсами пренебрегаем. При начальном числе ионов 106 (плотность ионов в прошедшем в область дрейфа ионном импульсе 1.35·105 см–3 при K1 = 1.5 см2/(В·с) и 1.4·105 см–3 при K2 = 1.57 см2/(В·с)) на расстоянии 40 мм от затвора ширина первого импульса с K1 = 1.5 см2/(В·с) составляет 0.14 мс, а второго 0.145 мс, при этом центры импульсов приходятся на моменты времени 5.1 и 5.32 мс соответственно, и пики разделяются. При начальном числе ионов 1010 (плотность ионов в прошедшем в область дрейфа ионном импульсе 1.84·108 см–3 при K1 = = 1.5 см2/(В·с) и 1.92·108 см–3 при K2 = = 1.57 см2/(В·с)) вследствие действия объемного заряда ионные импульсы уширяются и частично перекрываются. На рис. 6 видно, что зона перекрытия на расстоянии 40 мм от затвора составляет 0.25 мс и постепенно уменьшается с увеличением пройденного дрейфового расстояния. При этом разрешение, в общем случае определяемое как 0.5·(K2 + K1)/(K2 – K1), равно 22.

ЗАКЛЮЧЕНИЕ

Кулоновское взаимодействие между ионами, прошедшими в область дрейфа, может заметно повлиять на разрешение ион-дрейфового спектра. В работе представлена аналитическая модель, которая описывает динамику ионного облака с учетом действия объемного заряда при движении в ион-дрейфовом спектрометре: начиная с области ионообразования на стадии формирования ионного импульса затвором и при дальнейшем дрейфе сформированного ионного импульса в сторону коллектора. Представленная модель позволяет оценить степень влияния объемного заряда на возможные потери ионов и разрешение ион-дрейфового спектрометра. Влияние объемного заряда становится заметным начиная с плотности ионов 106 см–3. Сравнение результатов, полученных с помощью аналитической модели, с результатами численного решения исходных уравнений показывает, что они практически совпадают.

Работа частично выполнена в рамках НИР 00742019-0009 (номер гос. регистрации АААА-А19-119053190069-2), входящей в состав гос. задания № 075-00780-19-02 ИАП РАН.