Оценка влияния скоростного смещения в радиолокационных станциях с ЛЧМ-сигналом на границы устойчивости сопровождения входящих в атмосферу космических объектов

Многие измерительные системы, предназначенные для обеспечения космических экспериментов, включают в свой состав радиолокационные станции (РЛС), использующие зондирующие сигналы с линейной частотной модуляцией (ЛЧМ). ЛЧМ-сигнал обладает той особенностью, что при измерении дальностной координаты наряду с флуктуационной появляется скоростная ошибка AR ^ [1], пропорциональная радиальной скорости У д (Ғ) движения космического объекта (КО), а при использовании схемы подстройки (гетеродинирования) частоты-разности между радиальной v ^ (t _n ) и опорной у™^ ) (соответствующей опорному значению частоты) скорости

Ғ

AR _n = k _v {v _R (t n ) - У оп (t_n)},    k _v = Т зс— ,    АҒ = Ғ н - Ғ к ,

АҒ где тзс - длительность зондирующего сигнала; Ғ - несущая частота; АҒ - частотная девиация ЛЧМ-сигнала; ky - коэффициент скоростного смещения; Ғн и Ғк - мгновенное значение частоты в начале и в конце излучения зондирующего ЛЧМ-сигнала.

Из анализа (1) следует, что при известном значении радиальной скорости движения КО можно положить v R ⁿ (t _n ) = V R (t n) и, следовательно, в этом случае скоростная ошибка равна нулю. В реальных условиях значение V R (t _n ), как правило, точно неизвестно, и в качестве v R ⁿ (t _n ) приходится использовать значение радиальной скорости, получаемое в процессе оценки параметров движения КО, в результате чего скоростная ошибка в общем случае отлична от нуля и зависит от ошибки оценки радиальной скорости.

Наличие скоростного смещения позволяет в принципе использовать ЛЧМ-сигнал для отстройки эхосигналов от подстилающей поверхности и плазменного следа от эхосигнала сопровождаемого объекта [2]. Однако, с другой стороны, наличие скоростной ошибки не только ухудшает точностные характеристики оценки дальности, но и может привести к потере устойчивости сопровождения КО.

В [3, 4] проведено аналитическое исследование влияния наличия скоростной ошибки в измерениях дальности на точностные характеристики и границы устойчивости алгоритмов определения параметров движения входящих в атмосферу КО. При этом рассматривались фильтры с постоянными параметрами сглаживания, соответствующими установившимся значениям переменных параметров оптимального фильтра Калмана.

Настоящая работа посвящена сравнительному исследованию влияния наличия скоростной ошибки в измерениях дальности на точностные характеристики и границы устойчивости алгоритмов оценки параметров движения входящих в атмосферу КО, построенных на основе фильтров с постоянными параметрами сглаживания и оптимальных калманов-ских фильтров. Исследование проводится как аналитическими методами, так и методами моделирования на ЦВМ.

• 2.    Основные соотношения фильтров

При решении задач обеспечения устойчивого сопровождения КО полиномиальная модель движения хорошо зарекомендовала себя на практике. При этом в процессе фильтрации на внеатмосферном участке полета, как правило, определяются только дальность и радиальная скорость, а старшие коэффициенты полинома вычисляются по первым двум на основе непосредственного использования уравнений движения КО [5]. На атмосферном участке полета в состав оцениваемых параметров дополнительно вводится либо баллистический параметр, либо радиальное ускорение.

Не нарушая общности получаемых результатов, будем полагать, что КО движется в направлении на РЛС и на него действуют только силы аэродинамического торможения. Тогда на внеатмосферном участке полета алгоритм оценки параметров движения неманеврирующего КО, построенный на основе соотношений дискретного фильтра Калмана, можно описать следующими соотношениями [5, 6]:

« R (t n ) = « R (t n ) + w (t n ) |R(t n ) - R ^э (t n ) o R t n ) = A (t n ) a R (t n - i ),

^O R ^(t n) =

R(t n )

V R (t n )

w (t _n ) =

W R (t n ) ^ У Д ^{( t} n)

A (t n ) =

w ^ (t n ) = к R^^^(R n ),  (ц = R,v r ) ,

1 T n

0   1

_                    к (t_n )к э, ,(t_n )

К „„(tn) = K*^tn) - 2 T ' RR’ _,  (ц = R, VR), у (Rn) + КRR(tn)

^T n — "tn

^{— t} n - 1 ,

где «r(tn) и aR(tn) - векторы-столбцы оцененных и экстраполированных значений параметров движения; w(tn) - вектор-столбец весовых коэффициентов; A(tn) - матрица экстраполяции координат с tn-1 на tn момент времени; R(tn) = Rn - измеренное значение дальности до КО с дисперсией a2(Rn); К^(tn) и K^tn) — элементы корреляционных матриц ошибок оценок К(tn) и ошибок экстраполяции:

К ^э (t _n ) = A (t n ) [ К (t _n - i ) + К д ( і _п ) ] А^т (t n ),

^К Д ⁽ п ) ^—

С 0

0  С і

o²(R n - i ).

Здесь К д (С) - диффузионная матрица; С о и С 1 — коэффициенты диффузии, введение которых обеспечивает ограничение эффективной памяти фильтра [7].

Алгоритм оценки параметров движения КО в верхних слоях атмосферы описывается теми же соотношениями (2) - (8) с той лишь разницей, что р, v — R, у д , а д , а

	1	Т п	Т 2 /2		C o	0	0
A (t n ) —	0	1	T п	,   К Д (t n ) —	0	С 1	0	a 2 (R n - i )
	0	0	1		0	0	С 2

	R(t „ )		№ д ( З п )
(t n ) —	У д (t n ) orM	,   W (t n ) —	^ Rr ( t n ) ^ Hr ( t n )	,                                   (9)

• 3.    Характеристики атмосферных фильтров

При входе КО в атмосферу появляется ускорение аэродинамического торможения:

а д (t o ) — - 2 7р(H o )у o У д (t o ),                                (11)

где 7 - баллистический параметр КО; y o и у д (t o ) - модуль скорости и радиальная скорость движения КО в момент времени t o ; p(H o ) - плотность атмосферы на высоте H o ,

p(H _o ) — р ₀ ехр {- 3H _o } , p _o — 1.22 кг/м ³ , 3 — 1/7170 м 1 . Н(t i ) — Н(t o) +H o (t i - t o ).

При этом (11) удается проинтегрировать и получить, что на отрезке времени

AR — ti - to при ATi/т ^ 1 изменение дальности, радиальной скорости и радиального ускорения движения КО можно описать следующими приближенными выражениями [3, 4, 8]:

R(ti) — R ^6a (t i ) + а д (^)т ² ехр { AT i /т } ,                        (12)

Уд (ti) — уДа(tг) + ад (to)T ехр{ ATi/т}, адЗЗ — ад(to) ехр{АТі/т},

R6a(ti) — R(to) + vд(to)AТi,     VR(ti) — уд(to), т — 1/3|Ho| — 1/3vo sin Ө, где R6a(ti) и уда(^) - значения дальности и радиальной скорости в момент времени ti > to, вычисленные в предположении отсутствия аэродинамического торможения, Ө - угол входа КО в атмосферу.

Пусть при оценке параметров движения КО на внеатмосферном участке траектории используется фильтр с достаточно большой эффективной памятью, когда, например, в (8) C o и С 1 стремятся к нулю [7]. Тогда можно считать, что к моменту времени входа в атмосферу, оцененное значение дальности и радиальной скорости практически совпадают с истинными значениями и, следовательно, при t i > t o

R^6a(ti) — R(t o ) + У д (t o )AТ i — R(t o ) + У д (t o )AТ i .

Вводя следующие обозначения:

«(t i ) = R(t i ) - R ^6a (t i ),      «(t i ) = R(t i ) - R ^6a (t i ),                      (13)

«(t i ) = R(t i ) - R ^6a (t i ),      « ^э (t i ) = R э (^) - R ^6a (t i ),

УК(^) = VR(ti) - Уд (ti), Ук(ti) = VR(ti) - Уд (ti),   ^(ti) = Уд(ti) - Уда (ti), aK(ti) = aR(ti), aK(ti) = aR(ti), aa(ti) = aR (ti), перепишем выражения (2) и (3) для оценок в виде aK(tn) = «^(tn) + w(t„) {«(tn) - «э(tn)} ,

« « (t n ) = A (t n ) a _K (t _n- i ),                                  (14)

«R (tn) = aK(tn) + «Ra(tn), aK(tn) = \\K(tnK(tnK(tn)\\T, a^(tn) = \\R 6a(tn)yRa(tn)aRa(tn)hT, где w(tn) и A(tn) определены в (9) - (10).

После несложных преобразований соотношения фильтра (14) можно представить в следующем более удобном для дальнейшего анализа виде:

R(t n ) = R ^6a (t n ) + «(t n ), У Д (t n ) = y R ^a (t n ) + «(t n )/T, a R (t n ) = K(t n )/T 2 ,      (15)

R ^6a (t n ) = R(t o ) + У R (t o )AT n ,   y R ^а (t n ) = У д (^),

K(t n ) = Q n «(t n - 1 ) + W n { «(t n ) - Q n «(t n - 1 ) } , Q n = 6Хр { Т „ /т } ,

Q n ^D(K- n — i ⁾

Q n D(K n - i ) + C72(« n ) ,

D(« n ) = W nC 7 2 (« n ) =

Q n D(K n - i )cr²

QnD(Kn-i) + C72(«n) , где D(«n) - алгоритмическое значение дисперсии оценки величины «(tn); «(tn) - измеренное значение величины «(tn):

«(t n ) = «(t n ) - AR n + ^(t n ).

Здесь AR n — скоростная ошибка, определяемая соотношением (1); ^ (t _n ) - нормально распределенный белый шум с нулевым математическим ожиданием и дисперсией 0' 2 (^ _n ).

Пусть при подстройке частоты гетеродина не учитывается наличие аэродинамического торможения. В этом случае следует полагать, что

УRП(tn) = УR(to) = УR(to), а в соответствии с (1), (12), (13), (15) и (19) имеем

«(t n ) = «(t n ) - k _v y _к (t n ) + ^(t n ) = «(t n )(1 - k _v /t ) + ^(t n ).                (20)

Пусть измерения являются равноточными: cr ² (« _n ) = cr ² (« _{n -} i ) = ст ² («) и равнодискретными: T _n = T _{n -} i = T . Тогда для установившегося режима: D(« _n ) = D(« _{n -} i ) = D(«) работы фильтра (17) – (18) имеем

D(«) = (1 - Q ^-2 ) ct² («) = wct ² («) , w = (1 - Q ^-2 ) .                  (21)

Реализацию фильтра (16) - (18) можно существенно упростить, если при п = 1, 2,... принять, что весовой коэффициент является постоянной величиной. Такие фильтры называются фильтрами с постоянными параметрами сглаживания или фильтрами с эффективной конечной памятью (ЭКП) [7]. В этом случае для формирования оценки «(t _n ) можно записать [4]: n

«(t n ) = ^ P i,n «(t i ), P i,n = wQ ^n-i (1 - w) ^n-i ,                    (22)

i =1

где P i, _n — импульсная переходная функция фильтра.

Для дискретной системы необходимым и достаточным условием ее устойчивости является ограниченность суммы:

Е Ы <М< го .                    (23)

г =1

Исходя из (22) имеем v       Q Q +1

-Q-у =

Так как Q >  1 , то рассматриваемый фильтр является устойчивым.

Математическое ожидание т(к, _п ) и дисперсия cr ² (« _n ) оценки «(t _n ) определяются выражениями

∞∞

т(к„) = Е P»,n т(,), СТ2(к„) = Е P»,n СГ2(«г), г=1                           г=1

которые с учетом (20) при п >  1 принимают вид

т(к _п ) = «(t n )(1 - k y /т), сг ² (к _п ) = D ( k „ ) = -ст ² (к).                 (24)

Таким образом, оценка величины «(t _n ) является смещенной, а дисперсия оценки cr ² (« _n ) совпадает с алгоритмическим значением дисперсии _D(« _n ).

Пусть теперь наряду с ранее сделанными предположениями при подстройке частоты гетеродина учитывается наличие аэродинамического торможения, так что

R r = V R (t o ) + <(t i ) = R R (t o ) + « э (^)/т.

Тогда в соответствии с (1), (12), (13), (15) и (19) имеем

«(t n ) = «(t n ) - k y {v _K (t n ) - Q«(t n - 1 )/T } + ^(t n ).

При этом соотношение для оценки (16) принимает вид

«^{( t} n ) = ^Q «^{( t} n - 1 ) ^{+ —} ^«^{( t} n ) ^{- k} y ^ _т ^- ^ _т ---j ⁺ ^^{( t} n ^{) - Q} «^{( t} n - 1 )^ =

= Q«(t n - 1 ) + w {y(t n ) - Q«(t n - 1 ) } , W = - (1 - k y /т),

«W = «^{( t} n ) ⁺      nM = Тр^ЧТРк .

(1 - ky/т )

По аналогии с (22) для определения импульсной переходной функции фильтра (25) можем записать следующее соотношение:

P i,n = WQ ⁿ

-

^г (1 - w ) ⁿ

-

г

,

с использованием которого нетрудно получить, что n

El Р г^ l = г =1

- (1 - 7)

1 - {Q | 1 - - (1 - ^^ ) | } ⁿ

¹ - { Q I ¹ - - (1 - ^k- ) | ) .

Из анализа (26) следует, что для того, чтобы рассматриваемая система в соответствии с критерием (23) была устойчивой, необходимо и достаточно, чтобы

^Q {^{i - -} 0 - ^kT^L)}

< 1,

или, после преобразования, ку <ку <ку,  ку = -т (q -1)-1,  к; = т (q + 1)-1.

Математическое ожидание и дисперсия оценки K(t _n ) (25) в установившемся режиме для рассматриваемого случая равны

т(к _п ) = «(t n ),   ст ² (« п ) =----;——

I - {Q [1

w ²

- w (1 - ^kv )]}

2 ^

При ку = 0 дисперсия оценки ст2(кп) совпадает с алгоритмическим значением (21). При других значениях ку отличие ст2(кп) от D^k^ будем характеризовать отношением к2(Кп) “ = D(k)

w

1 - {Q [1 -w (1 -    )]} 2 .

• 4.    Результаты расчетов на ЦВМ

Получить аналогичные аналитические оценки для калмановского фильтра, представляющего собой фильтр с переменными параметрами сглаживания (16) – (18), не представляется возможным. Поэтому оценки границ устойчивости для этого случая проводились с помощью расчетов на ЦВМ. Кроме того, расчеты на ЦВМ проводились для оценки их соответствия аналитически полученным данным для фильтров с постоянными параметрами сглаживания.

Оценка границ устойчивости определялась на основе анализа переходного процесса на выходе фильтра, т.е. анализировалась реакция фильтра на дискретную единичную функцию. При проведении расчетов полагалось, что

K(t 1 ) = 0, D(K 1 ) = ст ² (к) при п = 1,

K,(t _n ) = 1,   £(t _n ) = 0 при п > 1.

В процессе расчетов по формулам (25) для фильтра с постоянными параметрами сглаживания w = w o = const и по тем же формулам для фильтра с переменными параметрами сглаживания w = w _n , вычисляемыми по формулам (17) - (18), на выходе фильтра формировалась оценка

п

^(t n ) = '^Рг,п .

г =1

Момент потери устойчивости фильтра при заданном значении к _у фиксировался, когда на заданном интервале тактов работы фильтра п от 1 до N выполнялось условие

| «(t n ) | > А _к ,   1 <п < N.                               (29)

За граничное значение принималось максимальная величина к _у , при которой выполнялось условие (29).

В табл. 1 приведены результаты моделирования границ устойчивости фильтра с ЭКП и фильтра Калмана при различных значениях скорости входа КО в атмосферу V o [м/с], периода поступления информации Т [с] и угла входа КО в атмосферу Ө [град]. Момент потери устойчивости при заданном значении к _у фиксировался при А _к = 100.

Таблица1

Границы устойчивости фильтра с ЭКП и фильтра Калмана

Т, с «0, м/с Ө, град Фильтр с ЭКП           Фильтр Калмана $,, с к1и, с с ^, с к^,, с %, с 0.1 4000 15 –476.22 –476.20 3.42 3.44 –81.40 3.42 30 –126.75 –126.74 1.76 1.77 –39.80 1.76 45 –63.01 –63.00 1.24 1.24 –26.70 1.24 60 –41.82 –41.81 1.00 1.01 –20.96 1.00 75 –33.60 –33.52 0.90 0.90 –18.40 0.90 90 –31.30 –31.24 0.87 0.87 –17.60 0.87 8000 15 –118.20 –118.19 1.70 1.71 –38.20 1.70 30 –31.30 –31.24 0.87 0.87 –17.57 0.87 45 –15.50 –15.44 0.61 0.61 –11.16 0.61 60 –10.21 –10.20 0.49 0.49 –8.41 0.49 75 –8.20 –8.15 0.44 0.44 –7.14 0.44 90 –7.60 –7.59 0.42 0.42 –6.77 0.42 0.05 4000 15 –955.89 –955.84 3.42 3.45 –83.75 3.42 30 –255.27 –255.26 1.77 1.78 –42.20 1.77 45 –127.27 –127.26 1.25 1.25 –29.15 1.25 60 –84.66 -84.65 1.02 1.02 –23.33 1.02 75 –67.96 –67.95 0.91 0.92 –20.65 0.91 90 –63.38 –63.37 0.88 0.88 –19.86 0.88 8000 15 –238.11 –238.10 1.71 1.72 –40.68 1.71 30 –63.38 –63.37 0.88 0.88 –19.86 0.88 45 –31.51 –31.50 0.62 0.62 –13.35 0.62 60 –20.91 –20.91 0.50 0.50 –10.48 0.5 75 –16.76 –16.76 0.45 0.45 –9.18 0.45 90 –15.63 –15.62 0.44 0.44 –8.79 0.44 0.01 4000 15 –4793.10 –4793.05 3.50 3.46 –85.74 3.49 30 –1283.47 –1283.43 1.79 1.79 –44.14 1.79 45 –641.36 –641.34 1.26 1.26 –31.07 1.26 60 –427.40 –427.37 1.03 1.03 –25.28 1.03 75 –343.50 –343.45 0.92 0.93 –22.61 0.92 90 –320.50 –320.41 0.89 0.89 –21.83 0.89 8000 15 –1197.46 –1197.40 1.72 1.73 –42.62 1.72 30 –320.50 –320.41 0.89 0.89 –21.83 0.89 45 –160.10 –160.02 0.63 0.63 –15.29 0.63 60 –106.60 –106.59 0.51 0.51 –12.4 0.51 75 –85.70 –85.63 0.46 0.46 –11.07 0.46 90 –79.90 –79.88 0.45 0.45 –10.67 0.45 к^, ку - оценки коэффициента скоростного смещения, полученные в результате моделирования; ку, к у - теоретические значения коэффициента (27).

Из результатов, приведенных в таблице, следует, что для фильтра с ЭКП правые и левые границы устойчивости совпадают с теоретическими значениями (27) с точностью до второго знака после запятой. Правые границы устойчивости для фильтра Калмана согласуются c теоретическими значениями, полученными для фильтра с постоянными параметрами сглаживания, с той же точностью, а левые значительно сужаются.

На рис. 1–3 приведены примеры реализации процессов на выходе фильтра с ЭКП и фильтра Калмана от начала работы до момента фиксации потери устойчивости. Результаты расчётов показали, что если коэффициент скоростного смещения отрицательный, то процесс на выходе фильтров имеет колебательный характер. Момент потери устойчивости наступает раньше при увеличении значения коэффициента смещения по модулю. При этом фильтр Калмана по сравнению с фильтром с ЭКП теряет устойчивость значительно раньше.

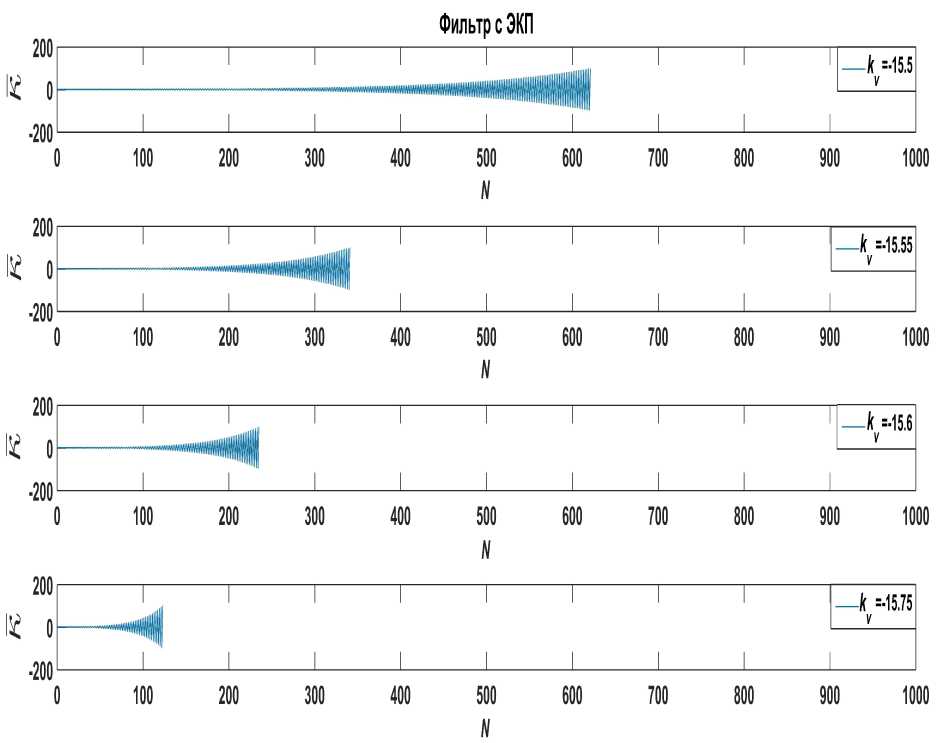
Рис. 1. Реакции фильтра с ЭКП на дискретную единичную функцию при отрицательных коэффициентах скоростного смещения к ^ . Период поступления информации Т = 0.1 с, скорость входа КО ^ 0 = 8000 м/с и угол входа Ө = 45° в атмосферу

В случае положительного коэффициента скоростного смещения к _у поведения обоих фильтров носит одинаковый характер.

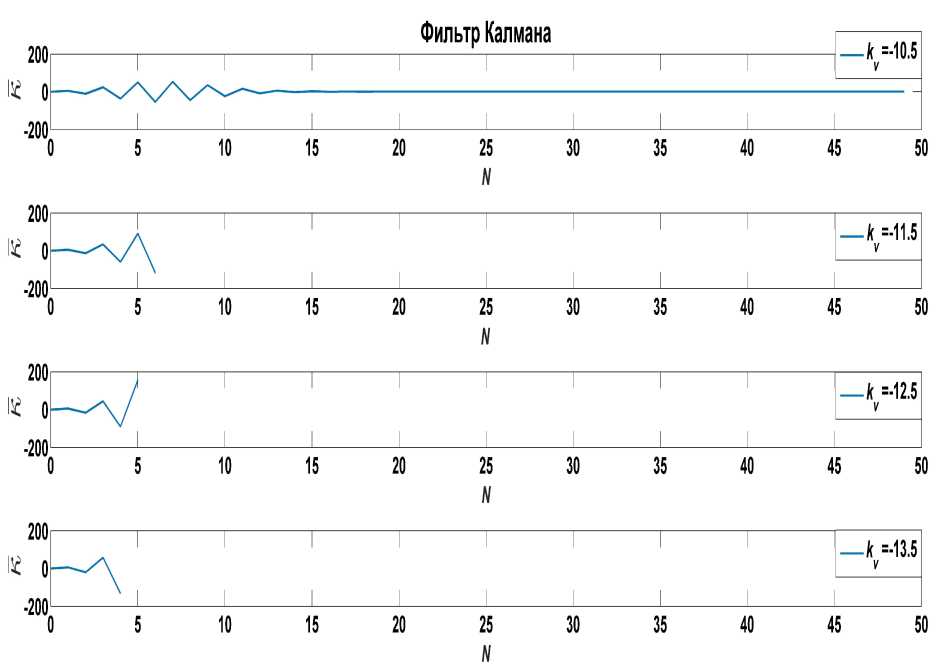
Рис. 2. Реакции фильтра Калмана на дискретную единичную функцию при отрицательных коэффициентах скоростного смещения к ^ . Период поступления информации Т = 0.1 с, скорость входа КО D 0 = 8000 м/с и угол входа Ө = 45° в атмосферу

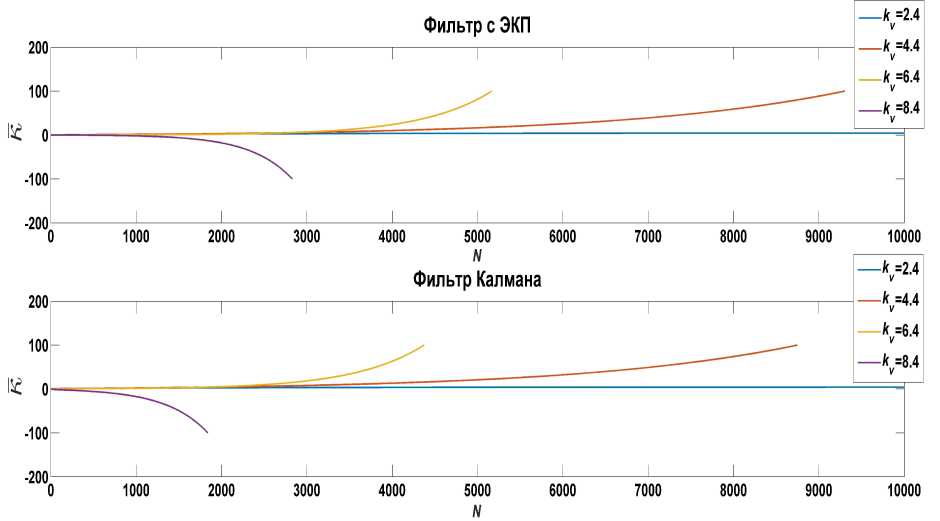
Рис. 3. Реакции фильтра с ЭКП и фильтра Калмана на дискретную единичную функцию при положительных коэффициентах скоростного смещения к ^ . Период поступления информации Т = 0.01 с, скорость входа КО ^ 0 = 4000 м/с и угол входа Ө = 15° в атмосферу

• 5.    Заключение

Проведенное аналитическое исследование показало, что для фильтров с постоянными параметрами сглаживания на атмосферном участке полета степень влияния скоростной ошибки зависит от способа учета наличия аэродинамического торможения при организации обработки информации. Так, при подстройке частоты гетеродина по значению радиальной скорости, полученной в процессе фильтрации на внеатмосферном участке полета, реализация фильтра является устойчивой при любом значении к у , оценка величины к(і _п ) является смещенной (24), а дисперсия оценки ст ² (к „ ) совпадает с алгоритмическим значением дисперсии D ( k „ ) (21). При подстройке же частоты гетеродина по значениям радиальной скорости, полученной с учетом наличия аэродинамического торможения, реализация фильтра может оказаться неустойчивой. Границы устойчивости определяются условиями (27). В пределах границ устойчивости оценка к(і _п ) является несмещенной, дисперсия оценки ^(к- п ) не совпадает с алгоритмическим значением D(R_Tl), а их отношение определяется исходя из (28).

Оценки границ устойчивости для калмановских фильтров, представляющих собой фильтры с переменными параметрами сглаживания (16) – (18), проводились с помощью расчетов на ЦВМ. Кроме того, расчеты на ЦВМ проводились и для фильтров с постоянными параметрами сглаживания с целью оценки соответствия границ устойчивости аналитически полученным данным. Для фильтров с постоянными параметрами сглаживания результаты моделирования показали хорошее согласование с теоретическими оценками.

Проведенное исследование позволяет в каждом конкретном случае, кроме традиционных параметров, предъявлять обоснованные требования к значению и знаку коэффициента скоростной ошибки измерения дальности при использовании ЛЧМ-сигналов, при котором обеспечивается устойчивая работа и заданные точностные характеристики алгоритмов сопровождения КО на атмосферном участке полета.

По теме статьи авторами будет сделан доклад на предстоящей II Международной научной конференции «Инжиниринг и телекоммуникации» Москва, 18–19 ноября 2015 года.