Оценка влияния тангенциальной составляющей скорости на распределение частиц в камере вихревого газогенератора

Г.Ф. Кузнецов г. Челябинск, ЮУрГУ

В статье рассматриваются вопросы организации рабочего процесса вихревого газогенератора, использующего угольную крошку, и дана оценка влияния на процесс аэродинамики камеры и теплофизических характеристик рабочего тела.

Частицы угля в камере газогенератора двигаются в основном под действием газового потока. Если газовый поток имеет тангенциальную составляющую, то и частицы приобретают движение по окружности. При этом на них начинает действовать центробежная сила, которая приводит к неравномерному распределению частиц в объеме камеры, которое может нарушить нормальный процесс газификации и привести к слипанию час тиц и к появлению спеков.

Для анализа этих явлений воспользуемся уравнением Навье-Стокса в цилиндрических координатах [1]; нужное для нашего анализа записывается следующим образом:

5у_ф !        , ^v

v

^ф , VI

St г йг г йф z Sz г

_М ЙР р Г Йф

+v У2уф+

2 йу_г г² йф

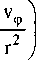
где У2уф

д2Уф 1 ауф 1 й\ , йг2 г йг г2 йф2 ’ v

р - плотность;

v - кинематическая вязкость;

Р - давление;

Ф, г, z - угловая, радиальная, осевая координаты.

Ограничимся решением одномерной задачи. Распределение скоростей воздуха в камере под действием постоянного градиента давления в азимутальном направлении

1 йФ Р

И---= +----= ц , г йф   2лК где R - радиус камеры.

Уравнение (1) можно записать следующим образом:

где т} - динамическая вязкость.

Решение будем искать при следующих граничных условиях:

v

= 0;          Уф = 0;

(r = 0); (R = r).                      (3)

Первое граничное условие реализуется, например, в вихревых трубах, где вращение в при-осевой области происходит по закону твердого тела, следовательно, на оси уф = 0. Второе граничное условие очевидно. Общее решение будем искать в виде уф = Ci? + С2г.                            (4)

Из уравнения (2) при г = 0, находим Ci=+^, а при г = R

С2 = R.

Таким образом, находим уф =-^(^-г),               (5)

Зт| у ¹

которая возрастает с увеличением ц (градиентом давления) и падает с ростом вязкости и удовлетворяет граничным условиям. Сравнивая с известными решениями для тангенциальной скорости в вихревой трубе [2], заметим, что наше решение имеет более монотонное распределение вдоль радиуса вследствие двух причин: 1) вязкость среды в камере существенно более высокая, чем вязкость воздуха (или другого газа); 2) уровень скоростей более низкий, чем в вихревой трубе.

Однако максимальная скорость в этом решении (5) существует и находится из условия

Теплоэнергетика

dvm

—2- = R-2r = 0 dr

на расстоянии г = R/2 от оси трубы.

Уравнение неразрывности имеет в нашем случае вид:

1£^+^=0. г сф Sz

Так как в нашей задаче v9 не зависит от ф, то vz = const, т.е. постоянное вертикальное течение накладывается на азимутальное.

Для оценки влияния распределения частиц в закрученном потоке реакционной камеры воспользуемся уравнением Больцмана [3], [4], [5]

N(r,v,t) = N0(v)-T(v)-^vVT + е , х 5N е , v -.SN

+—t(^v)s—-+—t(v)[vxHJ— ,     (8)

m Sv me         Sv в котором для нашей задачи второе и третье слагаемые правой части можно считать равными нулю, поскольку задача рассматривается в изотермических условиях без учета электрических сил. Тогда уравнение (8) можно записать следующим образом:

_ dN(r,t,v.3

N (г, v, t) = No + тсо2г— ----— ,        (9)

dv

N(r, t, уф) - локальная концентрация, угловая скорость;

т - время релаксации, т.е. время установления стационарного потока после прекращения внешнего возмущения.

После разделения переменных и подстановки

выражения для dv9 = — (R - 2r)dr, получим Зт]

-:b_(R/r-2)dr =

Зтсо г]

dN(r,t,V(p) Н(гдуф)-По

и после интегрирования запишем распределение концентрации частиц

’ ф

No

-ц -Rin—+2г ( R

_ е Зтсо2т|

(И)

где в качестве произвольной постоянной была выбрана величина InR.

Более удобно полученный результат можно записать в виде

No

= ехр

Зтсо2т]

• (12)

гда выше, чем в приосевой, что совпадает с результатами реальных исследований. При условии, что г] = 0, со = 0, г = 0, либо равна нулю одна из этих величин, второе слагаемое выражения (12) обращается в нуль. Физически понятно, что при нулевой вязкости частицы не изменяют своего первоначального распределения. Если скорость вращения отсутствует (со = 0), осевая скорость распределена вдоль радиуса равномерно и, следовательно, также первоначальное распределение в этом случае измениться не может. Очевидно, что на оси (г = 0) содержание частиц не может быть большим первоначального.

При увеличении г величина концентрации увеличивается, достигая максимальной вблизи г = R/2, там, где наибольшее значение тангенциальной скорости. Отметим, что полученное распределение скоростей и концентраций частиц быстрее реализуется для мелких фракций, так как для более крупных фракций требуется более продолжительное время для приобретения скорости потока газа и частиц.

Оценка характерного времени снижения до нуля тангенциальной скорости - времени релаксации - дает следующий результат. После прекращения действия давления (ц = 0), на поток действуют только силы, связанные с вязкостью (силы тяжести не учитываются)

dv m—= -6лг|\т0,                      (13)

dt где г0 - радиус частицы.

После разделения переменных и интегрирования находим

In v = vee т,                                (14)

m где т =--время релаксации.

6лт)г0

Для частиц размером ~3 мм это время составляет 1-3 секунды, что является достаточно близким к реальным условиям. Время контакта частиц, очевидно, будет такого же порядка, а это достаточно, чтобы состоялся тепловой контакт и их слипание.

Экспериментальным доказательством достоверности теории является то, что очаги шлакования возникают R/2 конической камеры.

Проделанный анализ неплохо объясняет сущность процессов при относительно небольших тангенциальных скоростях (диаметр камеры —1,5 м, скорость ~30 м/с), так как в соотношении (9) принято, что со ® const. Как известно, при больших скоростях центральные и периферийные слои вращаются по различным законам [6]. Для того, чтобы учесть эту особенность, воспользуемся уравнением Больцмана в следующем виде:

Анализ полученного выражения показывает, что при ц * 0 N(r, t, v,p) > Ng. Это означает, что в периферийной области концентрация частиц все

Из предыдущих выкладок следует, что

Кузнецов Г.Ф.                       Оценка влияния тангенциальной составляющей скорости

на распределение частиц в камере вихревого газогенератора

v =— Rr-r ; ц =--- ф 3r|V      /        2kR dv = —(R-2r)dr; v2 =-^-(R2r2-2Rr3+r4). (17) Подставляя (17) в (16), получим dN=3pr(R-2r)dr N-No Tp(R2r2-2Rr3+r4)'

/           1 \а ,                    (23) No 14 Зт] где а =--. wR Правая часть уравнения обращается в нуль при ^ = 0 и ^ = 1, поэтому между этими точками должен существовать хотя бы один экстремум.

r Введем безразмерную координату £ = — R dN 3л Rl"2?)dQ N-No TpR^(i-^2 J Правую часть запишем в виде двух слагаемых dN      Зр d^      d£ N-No тцК^(1-У (i-^)2 Тогда после интегрирования получим —— In——+ ln е             , (21) TpR 14             No Потенцируя, имеем 44       .      (22) Анализ последнего выражения позволяет сделать некоторые выводы. Концентрация частиц не отличается от начальной в центре камеры на максимальном радиусе, что соответствует известным представлениям закономерностей вихревых течений. Максимальное значение концентраций находится на расстояниях от оси, больших половины радиуса. В рассмотренной модели не учитывалась сила трения со стороны стенки, действующая на частицы. Любое торможение частиц на стенке камеры приводит к снижению их скорости и, следовательно, повышенной вероятности шлакования. Анализ спеков, возникающих в камере при превышении температуры 900 °C, показывает, что действительно спек имеет свое основание на стенке и вытянутую форму вдоль радиуса камеры примерно до его половины, т.е. в той его части, где реализуется наибольшая концентрация. Распределение частиц по размерам и, следовательно, массам также влияет на их концентрацию в камере. Анализ уравнения (15) показывает - времени пребывания наиболее крупных частиц в модельной камере достаточно, чтобы произошло выравнивание скоростей всех частиц. Это будет означать, что на стенке камеры окажутся, в первую очередь, крупные частицы, что и наблюдается в реальности. Для дальнейшего анализа запишем уравнение (22) в виде

Найдем точку экстремума, приравнивая нулю производную правой части а —1—е H+JL--1_е 1-5 = q, (24) (14)2     !-Ч14)2 J ИЛИ а—е                        (25) (i4)2 Откуда видно, что экстремум будет иметь место в точке ^ = 1/2. Для определения будет ли в этой точке максимум или минимум, определим знак второй производной в этой точке. Обозначим выражение перед последней скобкой. __1_ а—^е^=А,           (26) (i-d так это фиксированное число, не влияющее на знак второй производной, которая А-Э^Н-^о,       (27) и, следовательно, при ^ = 1/2 существует максимум распределения частиц. Этот результат соответствует анализу, проделанному при допущении со = const, свидетельство того, что для данного анализа такое допущение действительно можно принять. Литература 1.    Ландау Л.Д., Лифшиц Е.М. Гидродинамика. - М.; Наука, 1986. 2.    Кузнецов В.И. Полуэмпирическая теория противоточной вихревой трубы// В сб.: Некоторые вопросы исследования вихревого эффекта и его промышленного применения. - Куйбышев: КуАИ, 1974. - С. 19-25. 3.    Ферцигер Дж., Комер Г. Математическая теория процессов переноса в газах.-М.: Мир, 1976. 4.    Физический энциклопедический словарь. -М.: Советская энциклопедия, 1962. 5.    Пайерлс Р.Е. Квантовая теория твердых тел. — М.: Мир, 1956. 6.    Политое В.С., Кузнецов Г.Ф. О гидравлических сопротивлениях цилиндрических камер с закрученным потоком рабочего тела// В сб.: Некоторые вопросы исследования вихревого эффекта и его промышленного применения. - Куйбышев: КуАИ, 1974.-С. 228-232.

Серия «Энергетика», выпуск 6

51