Оценка влияния упрочнения дробью на предел выносливости деталей из стали 30ХГСА по первоначальным деформациям образца-свидетеля

Микушев Николай Николаевич, аспирант Киселёв Павел Евгеньевич, студент течение 8 минут дробью диаметром 2 мм при давлении масла 0,28 МПа. В качестве образцов-свидетелей использовались втулки с наружным диаметром 51,5 мм и внутренним 45 мм, которые применяются для определения остаточных напряжений по толщине упрочнённого поверхностного слоя методом колец и полосок [2]. На рис. 2 приведена эпюра осевых σz остаточных напряжений по толщине а поверхностного слоя в образце-свидетеле после ГДО, обработанном одновременно с гладкими образцами.

Расчётная часть исследований выполнена методом конечно-элементного моделирования с использованием комплекса PATRAN / NASTRAN. Конечно-элементные модели в осесимметричном варианте представляли собой четверть сечения детали с наложением соответствующих граничных условий. Для моделирования применялся плоский треугольный элемент типа 2D-Solid с шестью узлами. Моделирование остаточных напряжений по толщине упрочнённого поверхностного слоя гладких образцов осуществлялось методом термоупругости [3-8]. При проведении расчётов были приняты следующие допущения:

– все гладкие образцы и втулки (образцы-свидетели) при упрочнении получали одинаковые первоначальные деформации;

– первоначальные деформации являлись изотропными;

– деформации сдвига малы и при определении первоначальных деформаций они не учитывались.

Расчёты по определению остаточных напряжений в гладких образцах проводились в следующей последовательности:

– определение первоначальных деформаций в образце-свидетеле (втулка диаметром 51,5/45 мм/мм);

– расчёт распределения остаточных напряжений в гладких образцах по полученным значениям первоначальных деформаций образца-свидетеля;

– сравнение расчётных распределений остаточных напряжений в гладких образцах с их экспериментальными распределениями, приведёнными в работе [1].

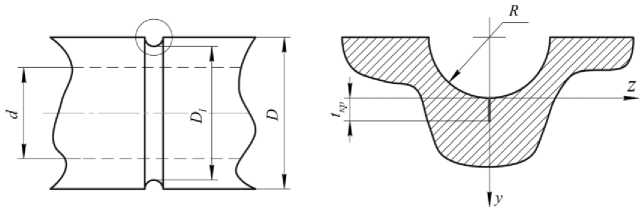
Рис. 1. Цилиндрический образец с надрезом и нераспространяющаяся трещина усталости

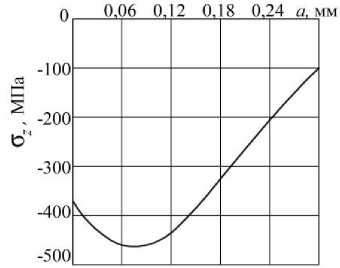
Рис. 2. Распределение осевых σ z остаточных напряжений в образце-свидетеле (втулка диаметром 51,5х45 мм) после ГДО

При определении первоначальных деформаций в качестве исходных данных использовалось экспериментальное распределение осевых σ z остаточных напряжений по толщине упрочнённого поверхностного слоя образца-свидетеля (втулки), приведенное на рис. 2. Установлено, что при принятых допущениях для получения совпадения распределения вычисленных по первоначальным деформациям и экспериментальных значений осевых остаточных напряжений в образце-свидетеле достаточно проведения трёх итераций.

Следующий этап расчётов выполнялся на конечно-элементных моделях исследуемых гладких образцов диаметром D =10 мм, D =15 мм, D/d =15/5 мм/мм и D/d = 15/10 мм/мм по первоначальным деформациям образца-свидетеля. При оценке приращения предела выносливости определяющими в соответствии с третьей теорией предельных напряжённых состояний являются осевые σ z остаточные напряжения [1, 9, 10], поэтому сравнение расчётных и экспериментальных распределений остаточных напряжений для исследуемых образцов было выполнено по осевой компоненте.

На рис. 3 представлены экспериментальные [1] и расчётные распределения осевых σ z остаточных напряжений по толщине а поверхностного слоя гладких образцов. Из приведенных на рис. 3 данных видно, что максимальное расхождение между расчётными и экспериментальными значениями наибольших сжимающих остаточных напряжений составляет 10% при D =10 мм, в остальных случаях расхождение не превышает 2%. Поэтому представляется возможным, используя первоначальные деформации образца-свидетеля, расчётным методом определить остаточные напряжения в детали, упрочнённой одновременно с этим образцом.

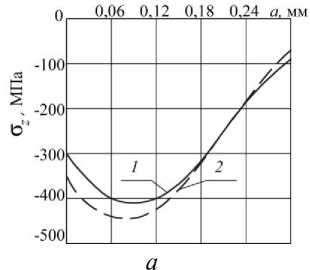
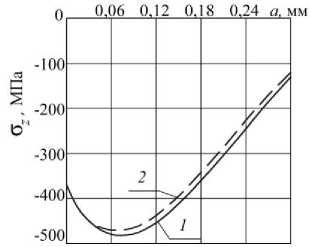
б

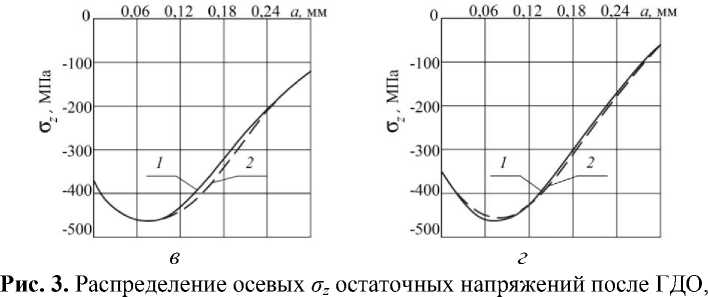
определённых экспериментально (1) и расчётом (2) в гладких образцах диаметром: а – D =10 мм, б – D =15 мм, в – D/d = 15/5, г – D=D/d =15/10

Полученные расчётные распределения остаточных напряжений после ГДО в гладких образцах использовались для расчёта распределения остаточных напряжений в образцах с круговыми надрезами полукруглого профиля радиуса R=0,3 мм, нанесёнными на гладкие образцы после упрочнения ГДО, то есть после опережающего поверхностного пластического деформирования (ОППД). Остаточные напряжения в образцах с надрезами вычислялись двумя методами: аналитическим [11] и численным с использованием программного комплекса PATRAN / NASTRAN [5]. Следует отметить, что остаточные напряжения, определённые двумя методами, имели хорошее совпадение.

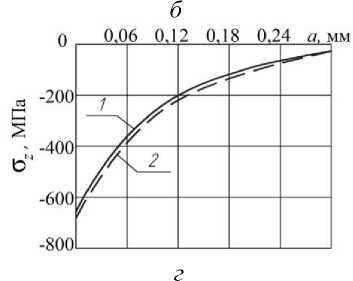
На рис. 4 приведены экспериментальные [1] и расчётные распределения осевых σ z остаточных напряжений по толщине а поверхностного слоя опасного сечения образцов с надрезами R =0,3 мм после ОППД. Можно видеть, что распределения остаточных напряжений, полученные по экспериментальным и расчётным эпюрам гладких образцов, отличаются по наибольшим значениям не более, чем на 6% (рис. 4, а – D =10 мм).

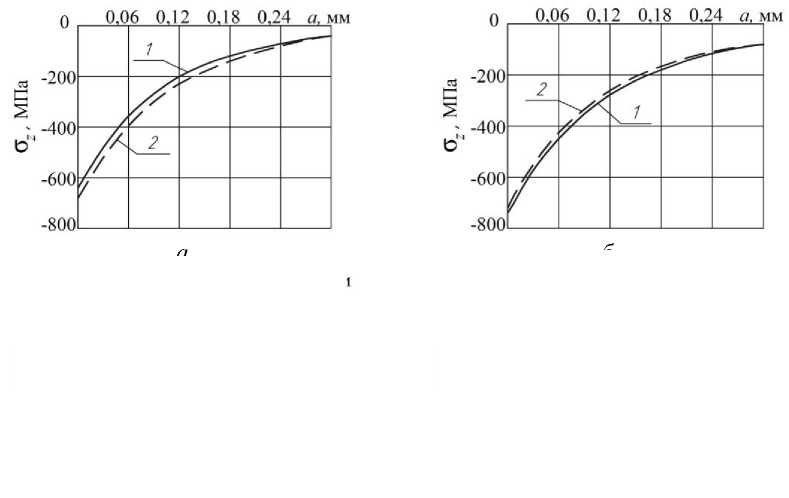
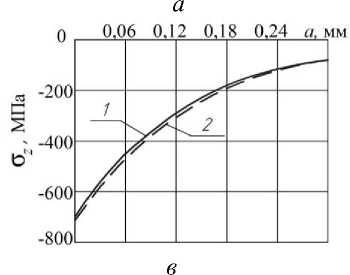
Рис. 4. Распределение осевых σ z остаточных напряжений в образцах с надрезом R =0,3 мм, вычисленных по экспериментальным (1) и по расчётным (2) данным: а – D =10 мм, б – D =15 мм, в – D/d =15/5, г – D = D/d = 15/10

Оценка влияния поверхностного упрочнения на приращение предела выносливости образцов с надрезами при изгибе в случае симметричного цикла (Act-1 ^а™ производилась по кри- терию среднеинтегральных остаточных напряжений σост [1, 9]

^{( Аст} - 1 ) рач = У Д ^СТ ост\

где V_CT - коэффициент влияния поверхностного упрочнения на предел выносливости по критерию ° ост ;

° ост

t p

=00216 Di1 —104 ^ 7

—

0154 о )

< D 1 7

,

= 2 1

^П 0

° z (§)

d§

;

°_z(§) - осевые остаточные напряжения в опасном сечении образца (детали) с концентратором по толщине поверхностного слоя а; § = ^а/ t ip -расстояние от поверхности опасного сечения образца (детали) до текущего слоя, выраженное в долях t кр ; t кр – критическая глубина нераспро-страняющейся трещины усталости, возникающей в упрочнённом образце (детали) с концентратором напряжений при работе на пределе выносливости.

Критическая глубина t кр нераспростра-няющейся трещины усталости, приведенная в табл. 1, определялась по зависимости, установленной на основании многочисленных экспериментов в работах [1, 12]:

где D 1 – диаметр опасного сечения образца (детали) с концентратором напряжений, d – диаметр отверстия.

Значения критерия среднеинтегральных остаточных напряжений ° _ост вычислялись по формуле (2) по толщине поверхностного слоя опасного сечения образцов, равной t кр , с использованием расчётных распределений остаточных напряжений, приведённых на рис. 4, и содержатся в табл. 1. Коэффициент V_a влияния поверхностного упрочнения на предел выносливости по критерию ° ост вычислялся по зависимости, установленной в работе [13]

^ = 0 , 612 — 0 , 081 а

где α σ – теоретический коэффициент концентрации напряжений, который определялся по графикам справочника [14] и представлен в табл. 1.

Таблица 1. Расчётные и опытные значения пределов выносливости образцов с надрезами

D , мм	d , мм	D 1 , мм	а °	w °	t кр , мм	° ост МПа,	( А ° — 1 ) расч, МПа  ,	( Л ° — 1 ) оп , МПа ,	Расхождение, %
10	0	9,4	2,7	0,393	0,203	-240	94	90	5
15	0	14,4	2,8	0,385	0,311	-196	75,5	77,5	3
15	5	14,4	2,8	0,385	0,303	-211	81,3	77,5	5
15	10	14,4	2,9	0,377	0,249	-218	82,1	80	3

Далее по формуле (1) вычислялись расчётные значения приращений предела выносливости ⁽Л° — i ) расч упрочнённых гидродробеструй-ной обработкой образцов с надрезами (табл. 1) и сравнивались с опытными значениями ⁽ ^° _{— 1} ) _оп , приведенными в работе [1]. Из табл. 1 видно, что расхождение между расчётными и опытными значениями приращения предела выносливости не превышает 5%, поэтому, используя результаты определения остаточных напряжений в образцах-свидетелях, представляется возможным прогнозировать предел выносливости поверхностно упрочнённых деталей в условиях концентрации напряжений с приемлемой для многоцикловой усталости точностью.

Выводы:

• 1.    Апробированный в настоящем исследовании метод расчёта остаточных напряжений в цилиндрических образцах из стали 30ХГСА после ГДО первоначальным деформациям образца-свидетеля показал, что расхождение между расчётными и опытными значениями остаточных

• 2.    При оценке влияния упрочнения ГДО на многоцикловую усталость при изгибе исследованных образцов из стали 30ХГСА с надрезами установлено, что использование вычисленных по первоначальным деформациям образца-свидетеля распределений остаточных напряжений позволяет прогнозировать приращение предела выносливости с точностью до 5%.

• 3.    Для прогнозирования предела выносливости поверхностно упрочнённой детали с концентратором напряжений вначале необходимо определить первоначальные деформации образца-свидетеля, обработанного одновременно с упрочняемой деталью. По первоначальным деформациям образца-свидетеля производится расчёт остаточных напряжений в опасном сечении упрочнённой детали. Критическая глубина t кр не-распространяющейся трещины усталости вычисляется по формуле (3), критерий среднеинтегральных остаточных напряжений ° ост – по

напряжений в гладких образцах не превышает 10%, в образцах с надрезами – 6%.

формуле (2), коэффициент ψ σ влияния упрочнения на предел выносливости – по зависимости _8.

• (4). После определения t кр , σ ост и ψ σ по формуле (1) рассчитывается приращение предела выносливости поверхностно упрочнённой детали с концентратором напряжений.