Оценка влияния воздушной среды на резонансные частоты и коэффициенты демпфирования солнечных батарей космических аппаратов, регистрируемые при наземных модальных испытаниях

Современные космические аппараты (КА) проектируются для эксплуатации на орбите в течение 12…15 лет. В связи с этим очень важным с точки зрения обеспечения усталостной долговечности конструкции солнечных батарей (СБ) является точное прогнозирование спектра их нагружения. Этот спектр включает в себя совокупность уровней нагрузок, действующих на СБ, и соответствующее этим уровням количество циклов нагружения.

Наиболее эффективным средством прогнозирования параметров нагружения СБ на орбитальном этапе эксплуатации является связанный расчет нагрузок для системы, состоящей из КА и СБ. При этом точность прогнозирования нагрузок, действующих на каждую СБ, в значительной степени зависит от точности конечно-элементной модели (КЭМ) самой СБ, так как при проведении связанного расчета используется КЭМ КА, которая подтверждена результатами модальных испытаний (МИ) КА для участка выведения и модифицирована для конфигурации корпуса, соответствующей участку орбитального полета.

Поскольку конструкция современных СБ представляет собой совокупность трехслойных анизотропных панелей неоднородной структуры, соединенных между собой упругими элементами, то из-за неопределенностей в жесткостных характеристиках некоторых элементов конструкции возможно наличие существенных погрешностей в динамических моделях конструкции СБ.

Верификация динамических моделей СБ в развернутом (рабочем) положении в естественных условиях эксплуатации на орбите из-за больших материальных и финансовых затрат нерациональна. Поэтому аэрокосмические компании во всем мире для проверки и подтверждения параметров динамических моделей СБ, как правило, проводят их наземные модальные испытания. Такой подход используется и РКК «Энергия».

С целью верификации КЭМ СБ для орбитального этапа эксплуатации в РКК «Энергия» проводятся МИ полноразмерных динамических макетов СБ, массово-инерционные и жесткостные характеристики которых соответствуют штатной конструкции.

Общий вид и основные геометрические размеры анализируемой СБ (площадь панелей, соприкасающихся с воздухом, S = 13,27 м²; масса — 58,5 кг) приведены на рис. 1.

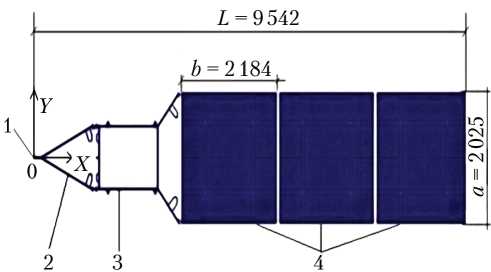
Рис. 1. Конфигурация солнечной батареи (СБ): 1 — привод; 2 — штанга; 3 — рама; 4 — панели; L — длина СБ; a — ширина панелей СБ; b — длина панели СБ

Фотография экспериментальной установки (ЭУ), в составе которой проведены МИ СБ, приведена на рис. 2.

Рис. 2. Экспериментальная установка для модальных испытаний динамического макета солнечной батареи: 1 — объект испытаний; 2 — силовая конструкция стенда

При испытаниях динамический макет СБ был вывешен вертикально, т. е. был закреплен за узел связи с приводом СБ. Такая схема закрепления позволила исключить из состава ЭУ специальную систему обезвешивания. МИ динамического макета СБ и анализ результатов этих испытаний проводились в соответствии с принятой в РКК «Энергия» методикой, которая описана в работе [1].

Математическая модель СБ

При разработке математической (динамической) модели конструкции СБ используется метод конечных элементов [2].

КЭМ СБ разрабатывается в системе координат OXYZ с началом в узле крепления СБ к ее приводу(см. рис. 1). Ось OХ лежит в плоскости симметрии (относительно координат ± Z ) и направлена от привода в сторону свободной кромки СБ; ось OZ перпендикулярна плоскости СБ; ось OY лежит в плоскости СБ и дополняет систему координат до правой системы координат. КЭМ СБ разрабатывается на базе соответствующей 3D -модели в среде программных комплексов MSC.NASTRAN и MSC.PATRAN . При этом для моделирования используются такие элементы, как QUAD4, BEAM, BUSH, CONM, SOLID, SPRING .

Для сформированной КЭМ колебания конструкции СБ описываются следующей системой уравнений в матричном виде [2]:

[ M k ]{ й } + [ C k ]{ U} + [ K ]{ u } = { F ( t )}, (1) где [ M_k ] — матрица масс конструкции; [ С_k ] — матрица демпфирования конструкции; [ K ] — матрица жесткости конструкции; { F(t) } — вектор внешних сил; { й }, { u}, { u } — переменные по времени векторы ускорений, скоростей и перемещений узловых точек динамической модели соответственно.

Однако для конструкций СБ, обладающих малой массой и большими площадями поверхности, воздушная среда при проведении МИ оказывает влияние на резонансные частоты и коэффициенты демпфирования. В связи с этим встает задача количественной оценки влияния воздействия воздуха на упомянутые характеристики СБ, которые определяются в процессе наземных МИ.

Для оценки влияния воздушной среды в работе используются два метода расчета.

Метод оценки A

В соответствии с методом А считается, что на элементарную площадку конструкции СБ площадью dS со стороны воздушной среды действует аэродинамическая сила, нормальная составляющая которой может быть представлена в виде [3]

-dm ---р V VC, dt 2 ^d

dS, (2)

где dm — присоединенная масса воздуха; ρ — плотность воздуха; V — скорость воздуха на поверхности СБ; C_d — коэффициент аэродинамической силы сопротивления.

В формуле (2) первый член соответствует инерции воздушной среды, а второй (нелинейный) член описывает ее сопротивление.

Выражение для силы, действующей на элементарную площадку dS при установившихся гармонических колебаниях, полученное с использованием экспериментальных данных, имеет вид [3]

dF = p V² — C — sin ® t--C,cos ® 1 1 cos a dS. (3)

I 4 m V         3 n ^d J

В этом выражении V — амплитудное значение скорости для элементарной площадки dS ; a — линейный размер (принимается ширина панели СБ); α — угол между вектором скорости и нормалью к площадке dS ; С_m — коэффициент присоединенной массы воздуха; ω — круговая частота колебаний.

Раскладывая вектор узловых перемещений { u ( x, y, t ) } конструкции СБ по формам тонов собственных колебаний, описываемых матрицей [ W ( x, y )], векторы перемещений, скоростей и ускорений определяются по формулам

{ u } = [ W ( x, y )]{ q }; { V } ={ u} = [ W ( x, y )] q ;

{ й } = [ W ( x, y )] q ;                 (4)

где { q }, q , q — переменные по времени векторы перемещений, скоростей и ускорений точки приведения динамической модели соответственно.

Используя формулы (3) и (4), система уравнений (1) трансформируется в совокупность уравнений установившихся гармонических колебаний СБ с учетом воздействия воздушной среды

M ki (H. ⁺ ■ - k, ™ k, q , + ™ „ q) ^- Q„ ' Q„     (5)

где ω _ki — круговая частота колебаний СБ в вакууме; ζ _ki — коэффициент демпфирования конструкции СБ в вакууме; Q_1i , Q_2i — обобщенные силы;

M ki = Л ’’Mx. y)Wi(^x’ y)dS,        (6)

S где mk(x, y) — распределенная масса конструкции для площадки dS;

[ Л _ о . J

- ^- P a^C m JJ cos ^{a dS} j ; ⁽⁷⁾

Q 2i = ^Q Bi q.i = q i | ^-:- p 9 i ^to B C d Л W I W | ^{cos a dS}\ (8) V 3 n         s               7

где Q_Bi — обобщенный интегральный параметр; ω _Bi — круговая частота колебаний СБ в воздушной среде; i — номер тона колебаний, i = 1, 2, …, N ; N — количество учитываемых тонов колебаний.

После преобразований совокупность уравнений колебаний (5) принимает вид

( M + M ) q + (2 ζ ω M + Q ) q + M ω ² q = 0.

ki Bi i           ki ki ki Bi i ki ki i

Разделив каждый член этого уравнения на ( M_ki + M_Bi ) = M_i *, получаем систему уравнений, по структуре аналогичную системе (5)

qi + 2ζBiωBi qi + ωBiqi = 0, где 2ζBiωBi = 2ζki ωki Mki /Mi* + QBi /Mi*.         (9)

Поскольку эффективная жесткость K_i i -го тона колебаний конструкции СБ при наличии воздушной среды не изменяется, то справедливо соотношение

K = ( M + M ) ω ² = M ω ² .     (10)

i ki Bi Bi ki ki .

Зная частоты колебаний СБ ω _Bi , зарегистрированные в процессе проведения МИ, и выделив из результатов расчета динамических характеристик определяемые по формуле (6) значения приведенных масс конструкции M_ki , частоты собственных колебаний СБ (в Гц) при эксплуатации их в условиях орбитального полета λ _ki находятся (после определения по формуле (7) значений эквивалентных присоединенных масс воздуха M_Bi ) из соотношения (10) по формуле

^ k - ⁽™ B, ^ 1 ⁺ M Bi IM ki ) /2 n . (11)

Анализ экспериментальных данных, обобщенных в работе [3], показывает, что значение коэффициента присоединенной массы C_m зависит от значения параметра St , эквивалентного числу Струхаля

St = – .

a ω

В этой формуле V — амплитудное значение скорости, м/с; a — характерный линейный размер, м; ω — круговая частота, 1/с.

Для условий проведения модальных испытаний СБ значение параметра St ≤ 1,0. Из экспериментальных данных, приведенных в работе [3], следует, что C_m ≅ 1,0.

В соответствии со статьей [3], значение коэффициента демпфирования C_d, полученное по результатам экспериментов для пластин, принимается равным 1,25.

Используя соотношение (9), делается оценка влияния воздушной среды на коэффициенты демпфирования ζ _i . Интегралы М_Вi и Q_Вi , входящие в формулы (7) и (8), определяются численно.