Оценка влияния взаимного расположения навигационной системы на точность определения местоположения беспилотного летательного аппарата

На точность определения пространственно-временных координат (далее – ПВК) беспилотного летательного аппарата (далее – БПЛА) оказывает влияние взаимное расположение спутниковой радионавигационной системы (далее – СРНС) и потребителя навигационной информации. Следовательно, возникает задача выбора рабочего созвездия СРНС, при котором будет обеспечиваться заданная точность измерений. Понятие «коэффициент геометрии» – мера уменьшения точности навигационных определений из-за особенностей взаимного расположения навигационной системы и потребителя. Геометрическое расположение спутников в пространстве определяется параметром Dilution of Precision (DOP); чем меньше этот параметр, тем точнее определяются координаты аппарата [1].

Оценка влияния взаимного расположения навигационной системы ...

Рами Мансур адъюнкт кафедры организации связи (и технической эксплуатации средств связи), Военный учебно-научный центр Военно-воздушных сил «Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина», город Воронеж. Сфера научных интересов: навигация беспилотных летательных аппаратов. Автор более 10 опубликованных научных работ.

Важным условием достижения высокой точности навигационных определений в СРНС является взаимное пространственное расположение рабочего созвездия и потребителя, при котором обеспечивается требуемая точность ПВК при заданном уровне погрешностей измерения псевдодальностей. На этом выводе основывается концепция коэффициента геометрии GDOP (геометрический фактор ухудшения местоопределения), являющегося мерой уменьшения точности навигационных определений в СРНС [6; 8]. Другими словами, GDOP описывает ошибку, вызванную относительным положением спутников рабочего созвездия.

Для выбора оптимального рабочего созвездия могут использоваться различные критерии, главный из которых – минимум дисперсий погрешностей навигационных определений. В данной статье рассматривается метод определения лучших значений GDOP, при котором можно определить оптимальное рабочее созвездие СРНС в зависимости от отношений между дисперсиями погрешностей навигационных определений и геометрическим фактором.

Решение задачи расчета геометрического фактора

Предлагается следующая последовательность расчета геометрического фактора. Пусть и представляет собой положение БПЛА относительно начала системы координат ECEF (геоцентрическая система координат, связанная с Землей). Вектор г представляет собой вектор смещения от БПЛА к спутнику, вектор s - положение спутника относительно начала координат (см. Рисунок 1).

Длина вектора г [9]

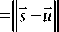
Геометрическая дальность r=С (T — Ts )=C A t .

Псевдодальность:

Р=С[((T +t„)-(Ts-St))]=С(T-Ts)+С(t„-St)=r+C(t„-St), где Ts – системное время, когда сигнал покинул спутник; Tu – системное время, когда сигнал достиг БПЛА; S t - смещение спутниковых часов от системного времени; t„ - смещение часов БПЛА от системного времени; C – скорость света.

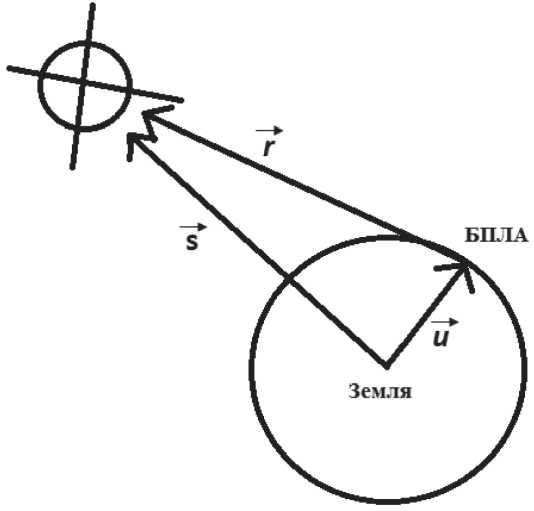
Рисунок 1. Определение дальности от спутника до БПЛА

Уравнения системы описывают работу на борту спутника при d t = 0

Р =||?- u |+ Ct_u .

Для четырех спутников:

P i =^( x i - x u ) 2 + ( У 1 - У и ) ² + ( z i - z u ) ² + Ct u ;

P 2 = j( x 2 - x u ) ² + ( У 2 - y u ) ² + ( z 2 - z u ) ² + Ct u ;

Р з =J ( x з - x u ) ² + ( у з - y u ) ² + ( z з - z u ) ² + Ct u ;

Р 4 =^( x 4 - x u ) ² + ( У 4 - y u ) ² + ( z 4 - z u ) ² + Ct u •

Пусть псевдодальность представляет собой [1; 16; 17]

Pj = ^(xj -xu ) + (У) -yu ) +(zj -zu ) + Ctu = f(xu ,yu ,zu ,tu ) , где Xj, yj,Zj - позиции спутника номер j в трехмерном пространстве и j = 1,4.

При аппроксимации позиции местоположения

/^р j =^( ^Xj — x u ) ² + ( y j — ^yu ) ² + ( z j — z u ) ² + Ct u = f ( x u , ^yu , z u , t u ) .

Учитывая, что истинное значение равно ожидаемому значению, получим xu = xu +A xu ; yu = yu +A yu ; zu = zu +A zu ; tu = tu +A tu • где xu - истинное значение; Xu - ожидаемое значение; Axu - ошибка измерения.

Тогда получим f ( xu , yu , zu , tu ) = f ( xu + A xu ,yu + A yu , zu + A zu , ^u + A tu ) •

С учетом расширения серии Тейлора

Оценка влияния взаимного расположения навигационной системы ...

f ( x u + ^A x u ,y u + ^A У и ,z u + ^A z u ,t u + ^A t u ) = f ( x u ,y u ,z u

. X ^{S f} ( x u ,y u ,z u ,t u ).

t +---^------------ -A x „ +

u)         5x u

^{S f} ( x u >y u , z u , t u ) .       ^{S f} ( x u ^u , z u , к ) .

+--^----"A yu +--^7----"A Zu +

S y_u                   O Z_u

^{S f} ( x u ,y u ,

Частные производные оцениваются следующим образом:

A

5 t u

z u , t u ) .

-----L A t„ +

где [15; 17]

^{S f} ( ^xu ^,yu , ^Zu ,i u ) __ X j - x u

^{S x}u                r j

^{S f} ( x u ^,yu , z u , iu )      y j - y u

^S y u    _л           r j

^{S f} ( ^Xu ^,yu , z u , iu ) __ z j ^- z u

c ri ^{A A A}.

S f ( Xu , yu , Zu

St u

A rj

^ _ C ,

—Cl • *

Xj ;

— Cl i ayj ’

--- Cl • A azj ;

rj =^(xj -xu ) +(yj -yu ) +(zj -zu ) •

axj,ayjи azj – направляющие косинусы единичного вектора, указывающего из БПЛА на j-й спутник.

Таким образом, [17]

a j = ( a xj , a yj , a zj ) •

С учетом	A P j - f 3j =	A xjxu A r ˆ j	■A xu	A y j - y u r ˆ j	■A y u	A z - —z ju A r ˆ j	■A zu	+ C A t u
				A P j = P j	- P j
и	A f 3j - p j	A v -V xjxu A rj	■A xu	* + y j - y u A r j	■A y u +	A zj - zu A r j	■A zu	- C A t u

^A P j = a xj ^A x u ⁺ a yj ^A y u ⁺ a zj ^A z u ^- C ^A t u •

Неизвестные величины могут быть определены путем решения системы линейных уравнений:

^A P 1 = a x 1 ^A x u ⁺ a y 1 ^A y u ⁺ a z 1 ^{A Z}u ^- C ^A t u ;

^A P 2 = a x 2 ^{A X}u ⁺ a y 2 ^A y u ⁺ a z 2 ^{A Z}u ^- C ^A t u S

^A P 3 = a x 3 ^{A x}u ⁺ a y 3 ^A y u ⁺ a z 3 ^{A z}u ^- C ^A t u S

^A P 4 = a x 4 ^{A x}u ⁺ a y 4 ^A y u ⁺ a z 4 ^{A z}u ^- C ^A t u •

В матричной форме [16]

A p =

"A p 1 "		axy	a y 1	a z 1	1 1		" A x u "
A p 2		a x 2	a y 2	az 2	1		A y u
A p 3	H =	ax 3	a y 3	a z 3	1	A x =	A Z u
_A p 4 _		_ ax 4	a y 4	az 4	1 _		- C A t u

.

A p = H A x .

В результате получим

Решение примет следующий вид:

A x = H ^{- 1} A p .

Основная формула псевдодальности, которая включает в себя координаты местоположения БПЛА ( x u , y_u , z u ) и смещение времени t_u , определяет полную точность определения местоположения координат приемника [7]:

5p= H 8 x + e , где e – вектор ошибок, и обычно предполагается, что его ожидаемое значение равно нулю: E [ t ] = 0 .

Если в небе присутствуют M спутников, тогда H представляет собой Mх4 матричных векторов, в которых каждый элемент является вектором управления между БПЛА и спутником; 5p представляет собой матрицу измерения псевдодальности размером Mх1 , 5х - вектор состояния навигационной ошибки размером 4х1, который включает поло- жение БПЛА и смещение часов; измерения псевдодальности.

В случае M =1 спутник e - представляет собой Mх1 вектор гауссового шума

5 x = H ^{- 1} 5p .

В случае M >  4 спутников

Ковариация 5 x [14]:

5 x = ( H T H ) ¹ H^T 5p .

cov

- T

( 5 x ) = E ( 5 x 5 x^T ) = E ( H T H ) ¹ 5p5p^T H ( H T H ) = ( H^TH )^{- 1} H^T 5p5p^T H ( H^T H )^{- T} =

= ( H T H )

¹ H^T cov ( 5p ) H ( H^T H ) T ,

где cov (5p) - ошибки псевдодальности. Они статистически независимы, что приводит к диагональной ковариационной матрице. Предполагается, что они имеют одинаковую дисперсию ( OUERE ) для каждого спутника. В этом случае cov (5p) = О"иere .

Поэтому [19]

E ( s x S x T ) = ^ U ere ( H T H )

¹ H T H ( H T H )

^T =^ UERE ( H T H ) - ^T .

Пока H^TH является симметричной, транспонирование не требуется [5; 7; 14]. cov ( 8 x ) = ct Uere ( H T H ) .

Оценка влияния взаимного расположения навигационной системы ...

Пусть G = ( H T H ) , и тогда			cov ( 8 x ) =	2 — uere G , следовательно			[2; 10; 14;15],
	"-1	cov ( x , y )	cov ( x , z )	cov ( x , b )		■ G xx	Gxy	Gxz	G xb
	cov ( y , x )	- 2	cov ( y , z )	cov ( y , b )	2	Gy x	G yy	G yz	G yb
	cov ( z , x )	cov ( z , y )	- 2	cov ( z , b )	= — UERE	G zx	G zy	Gzz	G zb
	cov ( b , x )	cov ( b , y )	cov ( b , z )	—b '		_ G bx	G by	G bz	G bb

Тогда [14]

• ^—Х ^{+ —} y ^{+ —} Х ^{+ —} b = ^— UERE ( G xx + G yy + G zz + G bb ) ;

• ^X ^+аУ ' ^a'- ^{+ —} b = ^— UERE -J( G xx + G yy + G zz + G bb ) ;

• V ^ x +^ У + ^— + — 2 = — UERE GD ^OP .

Поэтому [2; 7; 10; 18;19]

V — x + — 2 +— z +—b   ,----------------

^GDOP =^----- 2 ---------= G xx + G yy + G zz + G bb ;

^— UERE

;

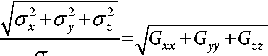
^— UERE

PDOP =

—x + —y   ,--------

HDOP =1 -----L= G xx + G yy ;

^— UERE

VDOP = -^z- =     ;

^— UERE

TDOP =-^ = G C^ .

^— UERE

Согласно формулам (1)–(5) [12; 13; 18]

PDOP ² = HDOP ² + VDOP ² .

GDOP 2 = PDOP 2 + TDOP 2 .

Использование PDOP описывает погрешность в трехмерном пространстве, HDOP – горизонтальную погрешность (полезную для позиционирования на земле), VDOP – вертикальную погрешность, а TDOP описывает временную погрешность [2; 16].

Таким образом, рассчитанные в соответствии с (6), (7) значения позволяют оценить оптимальные значения с учетом геометрического фактора.

Оптимальные значения факторов DOPs

Коэффициент потери точности GDOP является наиболее общей характеристикой, отражающей геометрию положения и оценку поправки часов. Как правило, значения GDOP больше пяти считаются слабыми, а при GDOP больше семи ответственные измерения обычно не производятся. Средняя величина HDOP и VDOP составляет около двух.

Минимальное значение GDOP = 1,5 достигается, когда потребитель находится в центре правильного тетраэдра [4]. Наилучшая геометрическая конфигурация видимых навигационных спутников имеет место, когда один из спутников находится в зените, а все остальные равномерно распределены по линии горизонта вокруг места расположения пользователя. В этом случае обеспечивается наилучшая точность определения координат местоположения пользователя [11].

Характеристики стандартной орбитальной конфигурации спутников в СРНС ГЛОНАСС таковы, что они с вероятностью 99,9 % и более обеспечивают в глобальной рабочей зоне видимость в любом 24-часовом интервале 4 и более спутников, при этом 4 спутника обеспечивают PDOP <  6 (в случае использования угла маски 5°), и среднее значение HDOP = 1,5 , a VDOP = 2,2 [4].

В Таблице 1 указаны значение DOP и их характеристики точности [12].

Значения геометрических факторов, обеспечиваемых орбитальной группировкой, и вероятности видимости P_N заданного числа спутников N в СРНС ГЛОНАСС приведены в Таблице 2 [11].

Таблица 1

Значения DOP и их характеристики точности [12]

Значение DOP	Точность	Описание
< 1	Идеальная	Рекомендуется к использованию в системах, требующих максимально возможную точность во все время их работы
2 - 3	Отличная	Достаточная точность для использования результатов измерений в достаточно чувствительной аппаратуре и программах
4 - 6	Хорошая	Рекомендуемый минимум для принятия решений по полученным результатам. Результаты могут быть использованы для достаточно точных навигационных указаний
7 - 8	Средняя	Результаты можно использовать в вычислениях, однако рекомендуется позаботиться о повышении точности, например, выйти на более открытое место
9 - 20	Ниже среднего	Результаты могут использоваться только для грубого приближения определения местоположения
21 - 50	Плохая	Обычно такие результаты должны быть отброшены

Таблица 2

Геометрический фактор в СРНС [11]

Параметры	Число видимых навигационных спутников ( N )
	4	5	6	7	8	9
P N	1	1	1	1	0,91	0,58
HDOP, K GH	1,41	1,26	1,15	1,03	0,95	0,89
VDOP, KGV	2,0	1,75	1,7	1,61	1,6	1,55
TDOP, KGT	1,13	1,03	1,03	0,95	0,93	0,91
PDOP, KGP	2,45	2,16	2,05	1,91	1,86	1,79
GDOP, KG	2,69	2,39	2,3	2,13	2,08	2,01
c X yz ( C/A,CT ), m	18,3	16,2	15,4	14,3	13,9	13,4
^Z ( P,BT ), m	1,83	1,62	1,54	1,43	1,39	1,34

Оценка влияния взаимного расположения навигационной системы ...

Метод определения оптимальных значений GDOP

В спутниковых радионавигационных системах точность определения местоположения координат БПЛА зависит от многих факторов, включая количество видимых спутников, значения геометрического фактора (DOP) и эквивалентной дальномерной погрешности (UERE), которая представляет собой общее влияние источников ошибок на каждое измерение псевдодальности [2]. Стандартное отклонение навигационной ошибки ст _С рнс можно представить как произведение GDOP и эквивалентной дальномерной погрешности определения местоположения [3; 9; 13]:

^ срнс - GDOP х ст _иЕКЕ . (8)

Согласно формуле (8) и предполагая, что эквивалентная дальномерная погрешность имеет постоянное значение, можно представить зависимость среднего квадратического отклонения навигационной ошибки от значения геометрического фактора (DOP) как показано на Рисунке 2.

Таким образом, эти две величины связаны между собой так, что с увеличением (уменьшением) значения одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз, следовательно, зависимость прямо пропорциональная.

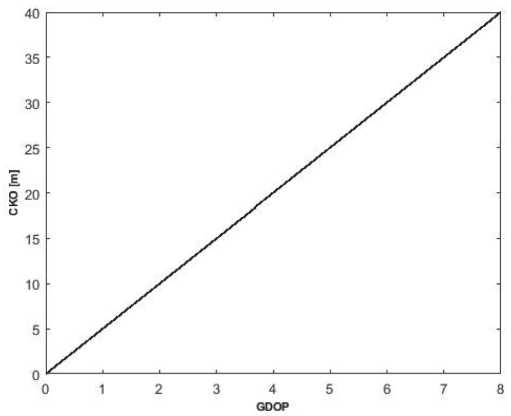
Рисунок 2. Зависимость СКО СРНС от значения геометрического фактора

Геометрический фактор может быть представлен также в другом виде [6; 7; 9;16] как

GDOP - [ tr ( HH ^T ) ^{- 1} ] ² , где tr ( ) - след матрицы.

Матрица градиентов H определяет геометрию взаимного положения навигационных спутников рабочего созвездия. Использование зависимости (8) позволяет сформулировать метод выбора рабочего созвездия СРНС с учетом геометрического фактора, который сводится к следующей последовательности действий:

а) для произвольно выбранной четверки СРНС определяется матрица градиентов H ;

б) предполагается, что значение эквивалентной дальномерной погрешности (UERE) для всех спутников одинаковое;

• в)    согласно (8) определяется стандартное отклонение навигационной ошибки ^ _СРНС ;

• г)    процедуры а)–в) повторяются для всех комбинаций четверок навигационных спутников, сигналы которых наблюдаются на входе приемника СРНС;

• д)    в качестве рабочего выбирается то созвездие СРНС, стандартное отклонение на

вигационной ошибки ст _СРНС которого будет минимальным.

Использование данного метода позволяет выбрать рабочее созвездие СРНС, обеспечивающее наибольшую точность определения координат БПЛА. Например, рассмотрим две группировки спутников: СРНС 1А, 2А, 3А, 4А и СРНС 1В, 2В, 3В, 4В (см. Рисунок 3) [13].

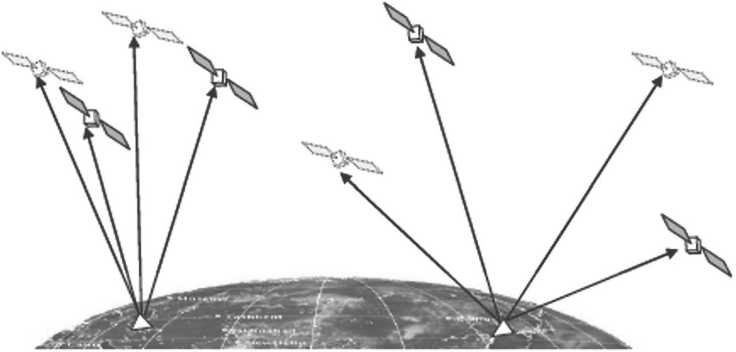
Хорошая геометрия (1-4) А

Плохая геометрия (1-4) В

Рисунок 3. Выбор рабочего созвездия [13]

Пусть конфигурация СРНС внутри группировок имеет разные коэффициенты геометрии и одинаковые эквивалентные дальномерные погрешности, как следует из формулы (8), то есть

^ срнс 1 = ^GDOPi х ct _{UERE i} ^;

^ СРНС 2 = ^GDOP2 ^x^ uERE₂ ;

° UeRE =^a UEBE1 = ^a UERE₂ •

Предположим, что аппаратура БПЛА принимает сигналы СРНС как первой, так и второй группировки. Первая группировка функционирует в штатном режиме, при котором в точке расположения аппаратуры приема, значение геометрического фактора

GDOP 1 = 2,5 . Вторая группировка СРНС в точке приема обеспечивает значение геометрического фактора GDOP 2 = 2,01 [4].

В связи с этим дисперсии эквивалентных дальномерных погрешностей определения квазидальностей до навигационных спутников внутри каждой группировки будут равны. В этом случае стандартное отклонение навигационной ошибки ст _СРНС имеет вид

^ срнс 1 GDOP_t ^ uere, --------=        - х------¹ .                             (12)

^ СРНС 2 ^GDOP2 ^a UERE2

Подставив в (12) значения геометрического фактора первой и второй группы СРНС, увидим, что стандартное отклонение навигационной ошибки определения ПВК первой группировки в 1,24 раза больше стандартного отклонения навигационной ошибки определения ПВК второй группировки. Таким образом, выбор второго созвездия в качестве

Оценка влияния взаимного расположения навигационной системы ...

рабочего позволит в 1,24 раза уменьшить СКО ошибки определения положения БПЛА в четырехмерном (пространственно-временном) измерении по сравнению со вторым созвездием.

Заключение

В статье рассмотрены вопросы навигационного обеспечения БПЛА с учетом влияния геометрического фактора на точность определения координат движения БПЛА.

В результате проведенного исследования определено, что геометрическое расположение спутников в пространстве определяется параметром Dilution of Precision (DOP). Чем он меньше, тем точнее определяются координаты аппарата; если параметр DOP увеличится вдвое, то и ошибка определения координат возрастет в два раза.

Выбор рабочего созвездия спутников производится по данным минимума дисперсий погрешностей навигационных определений. Это позволяет выбрать рабочее созвездие, обеспечивающее более высокие характеристики точности определения координат БПЛА. С этой целью был предложен метод выбора рабочего созвездия, учитывающий взаимное расположение навигационных спутников в созвездии.