Оценка воздействия космической погоды на синхронизацию времени в системе мониторинга переходных режимов

В последнее время в управлении производством электроэнергии используются метки времени от глобальных навигационных систем (ГНС) для синхронизации момента измерений в различных узлах крупных систем с целью получения фазовых сдвигов измеряемых сигналов. Здесь важным является точность в одновременности момента измерений, т.е. чтобы передаваемая с величинами измерений метка времени в различных точках была максимально синхронизирована для всех измерений. Телеметрия, принятая диспетчерским центром и обработанная оперативно-информационным комплексом с учетом меток времени, позволяет диспетчеру получить полную картину развития событий в случае аварий или нештатных ситуаций. Точ- ность отсчета времени приобретает еще большее значение в системах мониторинга с применением векторных измерений. Связь точности синхронизации по времени с погрешностью по углу измерения 1000000

определяется как At I мкс I =                 , отку- f[Гц]-3600•60

да для 50 Гц погрешность угла менее 1 мин. требует точности синхронизации 0.926 мкс. Согласно требованиям стандартов [1], для задач электроэнергетики необходимо поддерживать одновременность замеров на уровне 1мкс.

Глобальные навигационные системы (ГЛОНАСС – глобальная навигационная спутниковая система России, GPS – Global Positional System, система глобального позиционирования США) обеспечивают не только определение географических ко- ординат, но и точную синхронизацию часов приемников спутниковых сигналов для организации обеспечения единого времени в системах учета электроэнергии, телемеханики, АСУ ТП и релейной защиты и автоматики.

Причины исследований в рассматриваемой области подробнее изложены в работе [2]. Здесь остановимся на некоторых численных оценках воздействия природных явлений на синхронизацию времени в СМПР или в зарубежной литературе WAMS (система мониторинга переходных режимов – Wide Area Measurement System), которая построена на УСВИ или в зарубежной литературе PMU (устройство синхронизированных векторных измерений – Phasor Measurement Unit). Работа СМПР базируется на отметках времени, поставляемых глобальными навигационными системами типа ГЛОНАСС или GPS.

Причины и оценка ошибки синхронизации. Сначала рассмотрим причины появления ошибок в синхронизации времени. Заметим, что при высоте спутника ГЛОНАСС 19 100 км и его нахождении непосредственно над приемником время распространения сигнала составляет °° = 63.67 мс, 300000

где с= 300 000 км/с – распространения радиосигнала. Очевидно, что при нахождении спутника под углом к приемнику эта величина возрастает. Так, если угол возвышения удаленного спутника составляет α = 20^о, то при радиусе Земли r = 6366 км и высоте спутника непосредственно над приемником h = 19100 км разность во времени прохождения сигнала от спутников С и В до приемника А Δ t составит (рис.1):

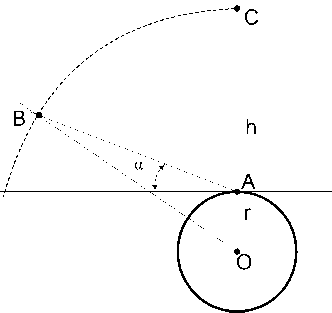
Рис. 1. Разность времени прохождения сигнала.

Fig. 1. A time difference of signal passing.

Л ВАО = 180 ° - (90 ° - Л а ) = 110 ° ;

sin Л ОВА =

r ■ sin Л ВАО r + h

6366 ■ sin 110 ° --------------= 0.235 ;

6366 + 19100

Л ОВА = 13.58 ° ;

Л ВОА = 180 °- 110 ° - 13.58 ° = 56.42 ° ;

( r + h )sin Л ВОА (6366 + 19100)sm56.42 °

АВ =-------------=--------------------= 22578 км ;

sin ЛВАО            sm110° дl = 22578 -19100 = 3478км ;

д t = д l / c = 3478000 / 300000 = 11.6 мс .

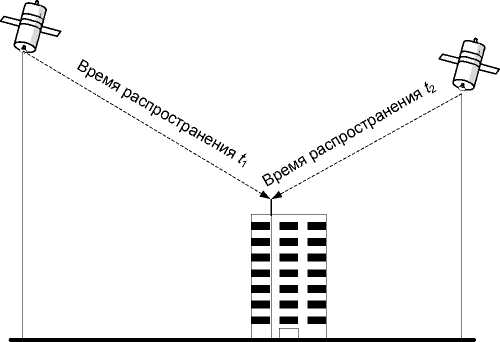
Как позиция приемника, так и синхронизация времени для него определяются при известных точном времени на спутнике и скорости распространения сигнала от спутника к приемнику. Рассмотрим это на простом примере (рис.2). Все необходимые переменные, связанные с приемником, а именно позиция L 1 и временная поправка Δ t распространения сигнала вычисляются с учетом времени его распространения t i и известном расстоянии между спутниками L 2 при известной скорости распространения сигнала с = 300000 км/с. L 2 определяется по известным координатам спутников [3].

Расстояние L 1

Расстояние L 2

Рис. 2. Определение позиции приемника и времени распространения сигнала до него.

Fig. 2. A receiver position definition and signal propagation time to it.

Для позиции на линии достаточно источников сигнала двух спутников

L 2 ^{+ (} t 1 ^- t 2 ) ■ ^c

• L¹ =          2        .

Для позиции на плоскости требуются три источника, а в пространстве – четыре. Следовательно, для определения расстояния и времени распространения сигналов спутников в 3-мерном пространстве должно наблюдаться не меньше четырех спутников. Заметим, что реально в отсутствии помех (гор, строений или зарослей) можно видеть до пяти … шести спутников. Расстояние до i -го спутника можно определить как R i = t i ٠ c . Но поскольку известны координаты только спутников, то расстояние до него в 3-мерном пространстве

Ri = ^(Xcn.i-Xnp.) +( Ycn.i-Ynp.) +(Zen.i-Znp.) + с ^дt , где неизвестные переменные позиции приемника Xпр. Yпр. Zпр. и погрешность времени распространения ∆t, т.е. необходима система с не менее, чем 4 уравнениями. Поскольку реально с позиции приемника наблюдается больше спутников, то систему можно решать методом наименьших квадратов. В результате получаем расстояния до спутников Ri, по которым можно вычислить и время распространения ti =Ri / c+Δt, необходимое для коррекции момента пуска АЦП устройства синхронизированных векторных измерений.

Понятно, что все известные значения находятся с определенной ошибкой. Ниже перечислены причины появления ошибок:

– Данные по позиции спутника известны с точностью до 1 ÷ 5 м.

– Часы спутника . При стабильности генератора 10^-13 ошибка часов за сутки без учета релятивистских явлений составляет примерно 10 нс. Их учет рассмотрен ниже.

– Влияние ионосферы . Ионосфера является частью атмосферного слоя между 60 и 1000 км над поверхностью Земли. Молекулы газа в ионосфере положительно ионизированы. Ионизация, в основном, вызвана солнечным излучением (только во время дня!). Определенное влияние на ионизацию оказывают геомагнитные возмущения в годы активности Солнца. Если сигналы от спутника проходят через вакуум со скоростью света, то в ионосфере скорость этих сигналов замедляется и, следовательно, более не является константой. Уровень ионизации меняется в зависимости от времени и места, усиливается днем и на экваторе, а также под влиянием солнечных штормов. Если влияние ионизации известно, то данный эффект можно компенсировать геофизическими коррекционными моделями. Кроме того, если скорость сигнала зависит от частоты, дополнительно можно сделать коррекцию с помощью двух частот приемника УСВИ, поскольку, чем выше частота, тем сильнее задержка сигнала. Следовательно, можно скорректировать скорость прохождения радиосигнала через ионосферу.

– Влияние тропосферы . Тропосфера является частью атмосферного слоя между 0 и 15 км над поверхностью Земли. Возникновение ошибок здесь обуславливается изменением плотности молекул газа и влажности воздуха. Плотность уменьшается с увеличением высоты. Увеличение плотности или влажности замедляет скорость сигналов спутника. Для коррекции данного эффекта используется простая модель на основе стандартной атмосферы (P) и температуры(T):H – высота, м; T = 288.15^oK – 6.5٠10^-3٠H, ^oK; P = 1013 мбар (T/288.15^oK)^5.256, мбар.

– Отражение . Сигналы спутников отражаются от зданий, деревьев, гор и т.д. и отклоняются перед получением приемником. Сигнал искажается из-за интерференции. Эффект отражения сигналов можно частично компенсировать выбором места расположения (без отражателей), хорошей антенны и времени измерения (рис. 3).

– Влияние приемника . Дальнейшие ошибки возникают из-за шума измерений приемника УСВИ и задержек по времени в приемнике. Сюда же входят так называемые радиопакеты, радиошумы, производимые электромагнитными процессами на Солнце, которые существенно снижают отношение “полезный сигнал/шум”. Современные технологии позволяют учесть такое влияние.

Позиция момента Т 1

Отраженный сигнал не принимается

'N УСВИ

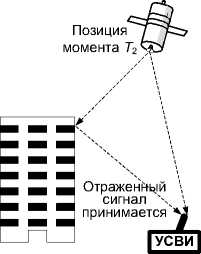
Рис. 3. Наложение отраженного сигнала из-за позиции спутника.

Fig. 3. A reflected signal interference because of a satellite position.

– Влияние взаиморасположения спутников с учетом их возможного затенения (DOP – dilution of precision - «снижение точности»). Точность любого измерения пропорционально зависит от величины DOP. Это означает, что если увеличить DOP вдвое, то ошибка в определении позиции возрастет также в два раза. Значение DOP является обратной величиной по отношению к объему четырехгранника, образованного позициями спутников и приемника. Наилучшее геометрическое расположение при максимальном объеме, и, следовательно, минимальном показателе снижения точности DOP. В работе J.-M.Zogg [2] дана таблица оценочных погрешностей по перечисленным причинам (табл. 1).

Таблица 1

Оценки погрешностей

Estimates of errors

Table 1

Причина погрешности	Величина погрешности в позиции, м	Величина погрешности во времени, мкс	Доля погрешности
Данные по позиции	2.1	7	0.195
Часы спутника	2.1	7	0.195
Влияние ионосферы	4.0	13.3	0.370
Влияние тропосферы	0.7	2.3	0.065
Влияние приемника	1.4	4.7	0.130
Влияние взаиморасположения спутников с учетом их возможного затенения	0.5	1.7	0.045
Общее среднеквадратичное значение	5.3	17.5	1.0

Таким образом, причины погрешности точного времени при передаче его сигналов от спутника к приемнику следующие: задержки в аппаратуре источника и приемника, время распространения радиосигнала от источника к приемнику, фазовые сдвиги из-за явлений отражения и преломления в ионосфере и тропосфере Земли, отставание или замедление времени на борту спутника из-за погрешности датчика времени и релятивистских явлений.

Задержки также делятся на детерминированные и недетерминированные. Первые измеряются при подготовке аппаратуры и затем учитываются при синхронизации бортового источника времени с эталонным источником времени на Земле. Такая синхронизация происходит один-два раза в сутки. Детерминированные погрешности в приемниках также измеряются и учитываются при работе. Погрешность недетерминированной задержки не превышает ±2нс [4]. Вклад в погрешность времени из-за релятивистских явлений (разностью времени, отсчитываемой часами на Земле и часами на борту движущегося спутника) оценен в работе С.Н. Филимонова [5], и на широте Москвы часы спутника опаздывают относительно наземных часов на 0.43 нс за каждую секунду или за 39 мин примерно на 1мкс. Следовательно, коррекция часов спутника должна выполняться с интервалом не более 36 мин, чтобы погрешность расхождения часов не превышала требуемые ±926 нс. Здесь следует отметить, что при единообразной коррекции эта погрешность не имеет заметного значения, поскольку в задачах СМПР важны не столько точность величины времени, сколько одновременность момента измерений в разных узлах большой системы.

Влияние геомагнитных штормов на синхронизацию. Выше отмечалось, что одной из причин появления ошибки синхронизации является геомагнитный шторм – нарушение в магнитосфере

Земли, управляемое изменениями в солнечном ветре [6]. Таким штормом управляет один из высокоскоростных потоков (вспышки мягкого и жесткого рентгена), либо поток извлечения массы короны, причем последний приводит к более существенным воздействиям. При оценке среднего времени до следующего события в вычислении вероятности возниковения при распределениях Бернулли, т.е. независимых событий, либо происходящих, либо нет с постоянной вероятностью возникновения, можно получить как

1 Р ( х ) = ,

• 1    + т

где τ – среднее время между событиями, т.е. сумма промежутков времени между событиями на число этих промежутков.Уровни активности Солнца хорошо отражаются количеством солнечных вспышек по датам (рис. 4). Он дает представление о том , в какие промежутки активности Солнца мы получим оценки вероятности возникновения штормовых геомагнитных возмущений. Диапазоны по датам и нижние уровни значения Dst, характеризующего величину шторма, к соответствующим вероятностям приведены в табл. 2 и показаны на рис. 5.

= 200

Е U ™ 150

о

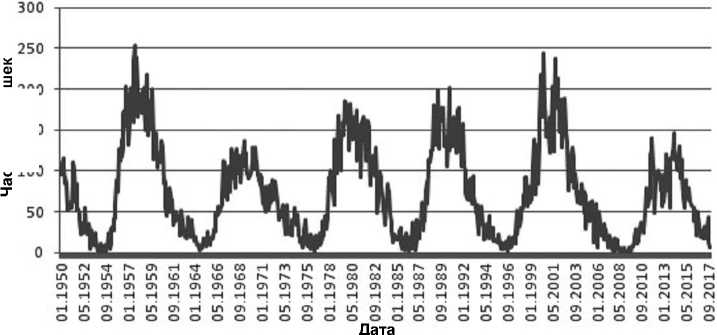
Рис. 4. Уровни активности Солнца по солнечным вспышкам (Использована база данных [7]). Fig. 4. The Sun activity levels on solar flashes (The database [7] is used).

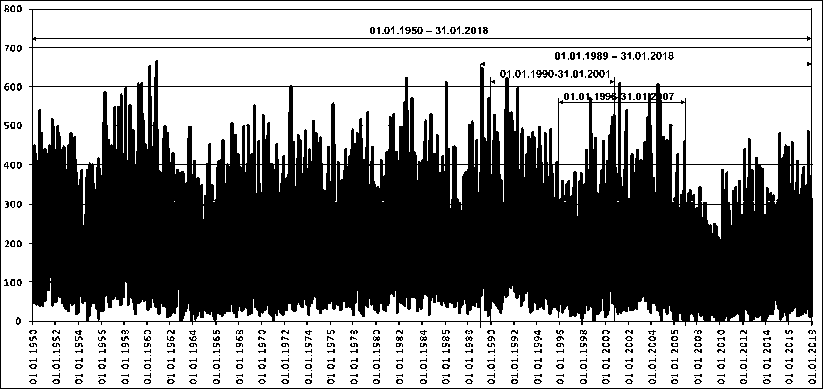
Дата

Рис. 5. Значения |Dst| за период 01.01.1950    31.01.2018 (Использована база данных [7]).

Fig. 5. |Dst| values during 01.01.1950   31.01.2018 (The database [7] is used).

Таблица 2

Оценка вероятности возникновения геомагнитных возмущений

Probability estimate of geomagnetic disturbance emergence

Table 2

Диапазон	| Dst |, нТл	τ , дней	P ( x )	Примечание
01.01.195028.02.2018	300	8.5	0.105 1/день	За период 67 лет
01.01.195028.02.2018	600	1380	0.209 1/год	За период 67 лет
01.01.198928.02.2018	300	10.4	0.088 1/день	За 28 последних лет
01.01.198928.02.2018	600	1404	0.206 1/год	За 28 последних лет
01.01.199001.01.2001	300	7.9	0.112 1/день	Между 2 минимумами
01.01.199001.01.2001	600	1794	0.169 1/год	Между 2 минимумами
01.01.199601.01.2007	300	10	0.091 1/день	Между 2 максимумами
01.01.199601.01.2007	600	607	0.375 1/год	Между 2 максимумами

Из таблицы видно, что для уровня штормов в 300 нТл вероятность такого возмущения в день составляет в среднем 10%, не сильно отклоняясь в различные периоды солнечной активности (8.8÷ 11.2%). При уровне |Dst| в 600 нТл вероятность этого события лежит в диапазоне 16.9÷37.5%, но уже в год. В периоды штормов от 300 нТл можно ожидать перерывов в связи с ГЛОНАСС, но здесь важна еще длительность такого перерыва, поскольку при коротких перерывах спасает местный источник точного времени, который синхронизировался по каждой временной метке спутников. Его стабильность обычно лежит в диапазоне 10-6 ÷10-12, что позволяет пропустить метки спутников в течение нескольких минут в зависимости от стабильности генератора приемника. Так, при стабильности генератора 10-10 погрешность в 1 мкс наступит уже через 2.8 ч. В табл. 3 даны вероятности того, что событие с |Dst|> 300 нТл продлится более 3 ч за различные периоды наблюдения.

Таблица 3 Оценка вероятности продолжительности геомагнитных возмущений от 3 ч и более

Table 3

Probability estimate of geomagnetic disturbance duration for 3 and more hours

Диапазон	Dst |, нТл	P ( x ), соб./год	Максимальный промежуток, часы
01.01.1950-28.02.2018	300	0.102	12
01.01.1989-28.02.2018	300	0.274	6

Другие причины природного воздействия на синхронизацию. Генератор приемника спасает и в случае прохождения грозы или присутствия солнечных радиопакетов (СРП), когда связь со спутниками ГЛОНАСС может прерываться на короткое время. Подобное влияние СРП на глобальные навигационные системы было отмечено в первый раз 5 декабря 2006 г. при солнечном минимуме. Этот пакет был величиной в 1 млн солнечных флюксов (один солнечный флюкс =1022 Вт·м2Гц-1); 6, 13 и 14 декабря в том же году зафиксированы события с меньшими потоками. Энергия на частотах ГЛОНАСС была достаточна для вмешательства в работу приемника информации в течение 10 ÷ 20 мин в каждом случае. Данные по позиции нескольких приемников плохо раскодировались (из-за неустойчивости связи) и были потеряны [8]. Следуя приблизительно на 12÷24 ч позади быстрых воздействий, эти пакеты представляли плазменные частицы, связанные с выбросом солнечной короны. Последние косвенно приводят к возмущениям в ионосферной электронной плотности на значительных площадях Земного шара и вызывают крупномасштабные (на10÷1000 км) структуры и градиенты, подобные волне, в ионосфере. Генерируются также небольшие структуры (меньше чем 1 км), и они вызывают сцинтилляцию (т.е. быстрые изменения по амплитуде и фазе) сигналов. Сцинтилляции∗ производятся сигналами, рассеянными в ионосфере из-за упомянутых выше ее неравномерностей, так называемых “пузырей” (рис. 6). Такие колебания обычно происходят в экваториальных и высоких широтах, где они представляют серьезную проблему. Во время экстремальных событий космической погоды ионосферная сцинтилляция может наблюдаться и в средних широтах в глобальной форме.

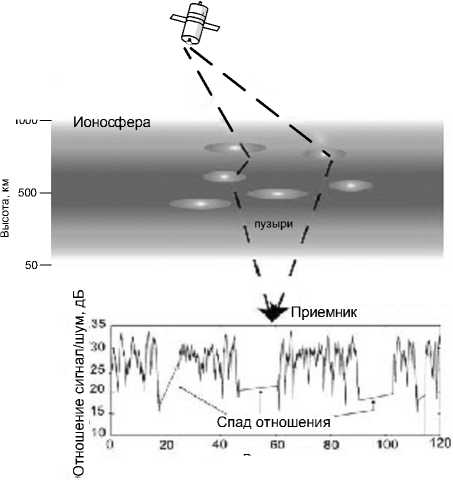
Время, с

Рис. 6. Влияние ионосферных неравномерностей на отношение сигнал/шум.

Fig. 6. Ionospheric irregularity impact on the signal/ noise factor.

Амплитудная сцинтилляция, вызывающая быстрые изменения в соотношении полезный сигнал-шум, может привести к потере сигнала во всех приемниках. Фазовая сцинтилляция, достаточно нару-

^∗ Сцинтилляция – (от лат. scintillatio – мерцание), кратковременная (10 ^–4 … 10 ^–9 с) вспышка, возникающая при взаимодействии заряженных частиц солнечного вещества с ионосферой Земли при солнечных штормах.

шающая фазу полезного сигнала, заставляет фазоотслеживающий цикл приемника терять блокировку, влияющую на прием важного навигационного сообщения данных, включающего спутниковые эфемериды (данные о положении спутника). Цикл отслеживания кода, измеряющего расстояние до спутника, довольно устойчив к фазовой сцинтилляции и обычно остается заблокированным. Потеря фазной привязки приемника, используемая в высоко интегрированных приложениях, особенно важна, поскольку эти приемники должны регулярно считывать спутниковое сообщение данных. Для смягчения этого спутник базируется на системах приращения, использующих длину символов сообщения в 500 символов в секунду, вместе с длиной половины кодера и повторения сообщений при ошибках пакета сообщения.

К сожалению, оценки разрушения сообщений ГНС, вызванного сцинтилляцией, связанной с суперштормом, плохие. Существующее предположение представляет полную потерю обслуживания сроком на один день, однако весьма вероятно, что будут периоды, когда, по крайней мере, одна группа спутниковых сигналов может быть получена, и синхронизация времени восстановлена. Для критической инфраструктуры рабочее предположение расширено на перерыв обслуживания сроком до трех дней и включает допуск на реинициализацию совокупности спутников (или системы приращения) после шторма.

Заключение

Современные электроэнергетические системы и, в первую очередь “умные” сети, используют временные метки глобальных навигационных систем для синхронизации измерения векторов токов и напряжений. Однако существует ряд природных и технических явлений, отрицательно воздействующих на выполнение такой функции ГЛОНАСС. К природным явлениям относятся геомагнитные бури, сцинтилляции, грозы, а к техническим можно отнести надежность функционирования технических средств ГНС, в том числе, погрешности измерения времени, окружение антенн приемников сигнала спутников ГЛОНАСС. Оценка вероятности событий, связанных с геомагнитными штормами по базе данных [7], показала, что можно ожидать возмущения при |Dst| > 300 нТлот 38 до 76 событий в год, а из них длительностью более 3 ч один раз в 4…8 лет. Такие оценки указывают на необходимость резервирования автоматики управления режимами электроэнергетических систем с использованием ГНС менее совершенными, но автономными системами, не привязанными к ГНС.