Оценка возможностей применения непараметрического критерия для исследования зашумленных импульсных сигналов

Technical University named after A.N. Tupolev -KAI

Russia, Kazan

Master's student of the Department of Electrical Equipment Kazan National Research

Technical University named after A.N. Tupolev -KAI

Russia, Kazan

Master's student of the Department of Electrical Equipment Kazan National Research

Technical University named after A.N. Tupolev -KAI

Russia, Kazan

ESTIMATION OF THE POSSIBILITIES OF APPLICATION OF A NONPARAMETRIC CRITERION FOR STUDYING NOISY PULSE SIGNALS

В работах [1, 2] представлены результаты исследований применения алгоритма на основе критерия Уилкоксона для оценки и анализа различных зашумленных гармонических сигналов. В качестве шума использовался Гауссов шум. Особенностью применения данного алгоритма является отсутствие проведения процедуры предварительной фильтрации зашумленного сигнала. При этом зашумленный сигнал преобразуется в такой атрибут, как случайная ранговая функция. Характерной особенностью ранговых функций является наличие в них экстремумов в соответствующих точках анализа. При этом однозначность выделения данных точек достигается при использовании разности ранговых функций, а точность оценки их местоположения зависит от соотношения сигнал/шум. Исследования показали, что наиболее информативными элементами в ранговой функции являются точки местоположения амплитуд сигналов. Оценка местоположения данных точек позволяет оценить период сигналов.

В данной работе представлены результаты возможностей применения алгоритма на основе непараметрического критерия Уилкоксона для оценки отдельных параметров зашумленных импульсных сигналов. Для проведения исследований    были    выбраны последовательность импульсных сигналов треугольной формы с коэффициентом заполнения Кз =0,95 и одиночный треугольный импульсный сигнал. Для оценки степени искажения сигнала использовалось соотношение сигнал/шум следующего вида:

m = Δf/ϭ, где

Δf – приращение значения сигнала от нуля до амплитудного значения в точках дискретизации (шаг равен единице);

б - среднеквадратическое отклонение шума.

Алгоритм построения ранговой функции [1, 2] для N = щ (X) + n2 (Y) =5+5=10 был реализован на языке программирования Си. Максимальное значение суммы рангов равно 40, минимальное значение - 15. Для исследований был использован шум с нормальным законом распределения N(0,1) (Гауссов шум). Сигналы формировались в диапазоне от 0 до 39 единиц. Всего 40 точек для анализа. Значения ранговой функции формировались соответственно в диапазоне от 5 до 35 единиц включительно. На всех ниже приведенных рисунках графики ранговых функций и их разности представлены в масштабе 1:10.

На рисунке 1 представлена характерная статистическая выборка последовательности зашумленных импульсных сигналов треугольной формы. Амплитуда исходного (незашумленного сигнала) равна 15,57, приращение сигнала Af =1,73, соответственно m = 1,73. Выборка графика ранговой функции на рисунке представлена в форме квадратов.

Следует уточнить, что разброс значений представленного на рисунке графика ранговой функции и значений ранговых функций, полученных в результате статистических испытаний, в среднем отличаются на 3-5%.

Анализ поведения ранговых функций показывает, что местоположение ее точек перегиба совпадает с точками расположения амплитудных значений импульсного сигнала. При этом факт наличия точки перегиба зависит от соотношения сигнал/шум и их выделение в определенных случаях носит неоднозначный характер. В работах [1, 2] использовался эвристический подход для оценки местоположения характерных точек ранговой функции. Суть подхода заключается в том, что в нем предусматривается получение разности выборок X и Y (Y и X).

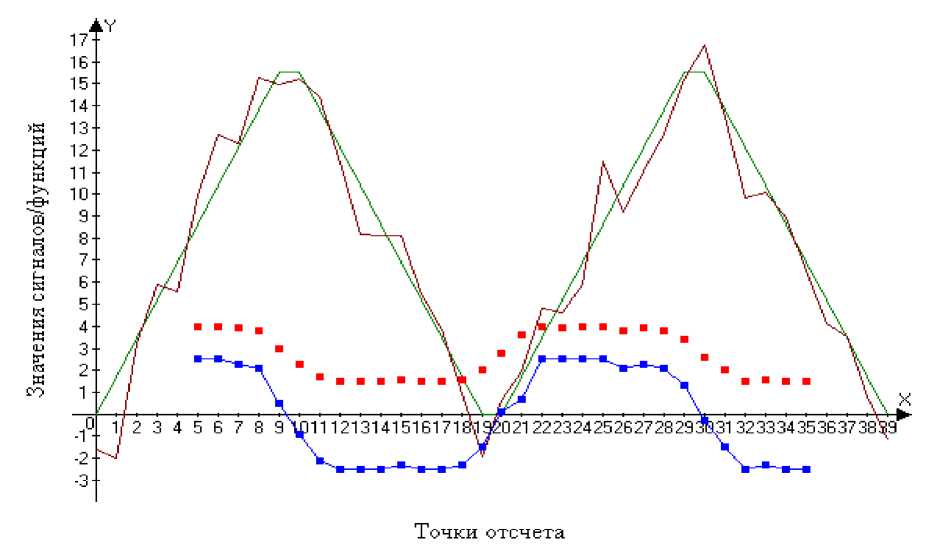
Рисунок 1 – Импульсный сигнал треугольной формы и графики ранговых функций

График разности выборок ранговых функций на рисунке 1 представлен в виде соединенных между собой квадратов. На графике видно, что точки местоположения амплитудных значений исходного незашумленного сигнала однозначно совпадают с местоположением точек разности ранговых функций при переходе от их положительных значений к отрицательным. Также из графиков видно, что местоположение точки начала возрастания незашумленного импульса совпадает с местоположением точки перехода разности ранговых функций от их отрицательных значений к положительным. Таким образом, оценка местоположения выше указанных точек позволяет определять период следования импульсов и их длительность.

На рисунке 2 представлена характерная статистическая выборка одиночного зашумленного импульсного сигнала треугольной формы. Амплитуда исходного (незашумленного сигнала) равна 15,57, приращение сигнала Δf =1,73, соответственно m = 1,73. Выборка графика ранговой функции на рисунке представлена в форме квадратов. Разность ранговых функций представлена в виде соединенных между собой квадратов.

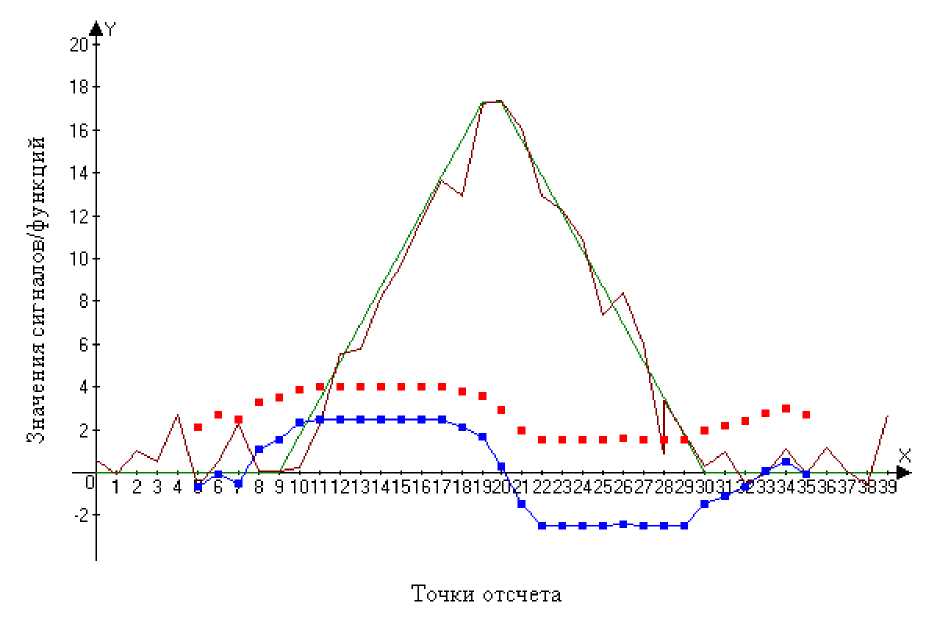
Рисунок 2 – Одиночный импульс треугольной формы и графики ранговых функций

Из графика видно, что как и в предыдущем случае, местоположение точки перехода разности ранговых функций от положительных значений к отрицательным совпадает с местоположением амплитудного значения сигнала. Как и в предыдущем случае, возможно оценить период следования импульсов.

В то же время, в интервалах отсутствия сигнала ранговая функция стремится к своему среднему значению (порядка 27 единиц). Разность ранговых функций в данном случае будет колебаться около нулевого значения с определенным средеквадратическим отклонением, которое в свою очередь зависит от соотношения сигнал/шум. При этом, имеют место переходы разности ранговых функций от положительных значений к отрицательным и обратно и эти переходы никак не связаны с харавктерными точками, связывающими точки разности ранговых функций и точки экстремальных значений сигнала. Очевидно, что при скважности импулсов Q существенно больше двух необходимо устанавливать порог для исключения из анализа точек «ложного перехода».

Таким образом, полученные результаты исследований применения непараметрического критерия Уилкоксона для анализа и оценки зашумленных импульсных электрических сигналов треугольной формы показывают, что данный критерий и алгоритм на его основе могут быть использованы для оценки отдельных параметров сигналов без проведения их предварительной фильтрации. При этом применение конкретного алгоритма для оценки параметров будет эффективным при условии, что форма сигнала априори известна.

Точность измерений оцениваемых параметров зависит от соотношения сигнал/шум и, как показывают статистические испытания, при его значении выше 1,8 ошибки определения местоположения точек экстремальных значений стремятся к нулю.