Оценка возможности определения поперечного профиля медицинского электронного пучка методом многоуглового сканирования для повышения точности проведения радиотерапевтических процедур

Современные тенденции усовершенствования подходов к лечению онкологических заболеваний ведут к усложнению планов облучения и увеличению разовых дозовых нагрузок, в связи с чем повышаются требования к точности доставки дозы [1]. Для уменьшения негативных последствий лучевой терапии необходимо не допускать переоблучения здоровых тканей или недо-облучения опухоли, как следствие, важно обеспечить постоянный высокоточный контроль пространственных и дозовых характеристик пучков до и во время проведения таких процедур. Важной характеристикой медицинских электронных пучков является поперечный профиль. При проведении электронной лучевой терапии поверхностных новообразований особенно важно обеспечить контроль данного параметра, так как поле облучения имеет сложную геометрию для обеспечения точного облучения опухоли и экранирования критических органов, играющих важную роль в жизнеобеспечении организма [1].

Булавская А.А. – ст. преподаватель, к.ф.-м.н.; Батранин А.В. – доцент, к.т.н.; Бушмина Е.А. – инженер; Черепенников Ю.М. – доцент, к.т.н.; Григорьева А.А. – инженер; Стучебров С.Г. – доцент, к.ф.-м.н. ФГАОУ ВО НИ ТПУ. Милойчикова И.А.* – мед. физик, к.ф.-м.н. ФГАОУ ВО НИ ТПУ, НИИ онкологии ФГБНУ ТНИМЦ РАН.

В клинической практике для того, чтобы измерить профиль электронного пучка, широко используют матричные детекторы. Такие устройства представляют собой матрицу, состоящую из определённого количества относительно небольших детекторов, расположенных на одинаковом расстоянии друг от друга. Матрицы могут состоять из набора ионизационных камер, полупроводниковых датчиков, диодов. Данный подход к диагностике медицинских полей имеет существенное преимущество – мгновенное получение двухмерного поперечного профиля медицинского пучка с абсолютными значениями доз в каждой точке. Однако результаты измерения поперечного профиля имеют низкое пространственное разрешение (около 10 мм) и не позволяют полноценно оценить сложное распределение интенсивности пучка [2-4]. Кроме матричных детекторов используют плёночные дозиметры или люминофорные экраны, которые позволяют измерять поперечный профиль пучка с высоким разрешением, однако такие устройства могут применяться только один раз или лишь несколько раз, что приводит к существенному повышению эксплуатационной стоимости этих устройств, помимо этого необходимо проводить контроль параметров сменных детекторов, а также не позволяет получать результат в режиме реального времени [5-7].

Другие существующие методы измерения поперечного профиля электронного пучка, такие как интерферометрия [8, 9], лазерное сканирование пучка [10-12], применение методов, основанных на регистрации вторичного излучения [13-18], в том числе переходного, характеристического, черенковского излучения и другие не предназначены для диагностики пучков относительно больших размеров (порядка десятков сантиметров). В связи с этим существует необходимость в наличии новых методов измерения поперечного профиля пучков ускоренных электронов.

Авторами данной работы был предложен метод многоуглового сканирования пучка, который заключается в математической реконструкции методом интегрального преобразования набора данных, полученных с помощью проволочного сканирования под разными углами [18-21]. В перспективе данный метод мог бы найти широкое применение как в медицине для контроля пространственных характеристик электронных пучков, так и для контроля качества существующих и оценки параметров разрабатываемых исследовательских ускорительных комплексов. Данная работа направлена на оценку возможности применения метода многоуглового сканирования пучка для контроля профиля медицинского электронного пучка.

Материалы и методы

Метод многоуглового сканирования пучка заключается в применении интегральных преобразований для восстановления поперечного профиля пучка, представляющего собой зависимость интенсивности излучения от координаты в измеряемой плоскости I o (x,y) , из набора зависимостей интенсивности излучения, попавшего в детектор, от его положения I(l,φ) . Для реализации данного метода необходима сканирующая детектирующая система, которая способна поступательно перемещать проволочный детектор в измеряемой плоскости, перпендикулярной плоскости распространения пучка в направлении l . Она также должна позволять изменять угол сканирования φ на определённое значение и проводить измерение повторно. На рис. 1 схематично представлен процесс сбора данных, позволяющий реализовать метод многоуглового сканирования пучка.

Методами обратного преобразования Радона (математическая реконструкция) из набора таких данных (проекций) восстанавливается двухмерный поперечный профиль пучка в измеряе- мой плоскости.

Рис. 1. Схема процесса сбора данных, позволяющего реализовать метод многоуглового сканирования: 1 – устройство для поступательного перемещения детектора;

2 – устройство для поворота детектора; 3 – пучок; 4 – проволочный детектор.

Тестовые распределения. Форма поперечного профиля пучка для каждого клинического случая подбирается индивидуально в соответствии с формой опухоли. На практике сложные распределения медицинского пучка формируются с помощью индивидуальных коллиматоров. Для оценки работоспособности метода многоуглового сканирования были использованы данные, полученные с помощью системы дозиметрического планирования процедур лучевой терапии «XiO» (Elekta Instrument AB, Stockholm, Sweden) [22]. Были выбраны два плана облучения опухолей кожи головы, в которых процедуры должны проводиться электронным пучком со сложной формой поперечного распределения с целью защиты критических органов.

Для каждой формы электронного пучка были получены два исходных изображения. Одно было получено искусственно таким образом, чтобы интенсивность излучения в каждой точке распределения могла принимать только одно из двух значений: 100% и 0%. Данное распределение является идеальной моделью профиля электронного пучка для облучения опухолей сложной формы и далее в работе будет называться «идеальный» профиль. Однако, в связи с тем, что в реальности имеет место рассеяние электронов на воздухе и на краях коллимационных отверстий, распределение интенсивности может отличаться от идеального. Поэтому с использованием реальных специально изготовленных индивидуальных коллиматоров с заданными размерами отверстий были экспериментально получены распределения пучка ускоренных электронов. Эксперименты были проведены на пучке электронов с энергией 6 МэВ медицинского линейного ускорителя «Elekta Synergy» (Elekta Instrument AB, Stockholm, Sweden) [23]. В качестве детекторов использовались плёночные дозиметры «Gafchromic EBT3» (Ashland Inc., Covington, Kentucky, United States) [24]. На рис. 2 представлены изображения тестовых распределений интенсивности электронных пучков, где идеальный – полученный на основе расчётов планирующей системы, и реальный – полученный экспериментально.

Процесс обработки данных. Для проведения исследования на первом этапе необходимо получить набор проекций под разными углами для каждого исходного изображения (рис. 2). Для этого с помощью программы «MatLab» (MathWorks Inc., Natick, Massachusetts, United States) [25] исходные изображения были представлены в виде матриц значений яркости изображений в каждом пикселе. Суммируя значения в каждом столбце, находилась строчка значений, представляющая собой проекцию данного изображения на ось, находящуюся под углом 0° к горизонтальной оси. Далее каждое изображение поворачивалось на фиксированный угол смещения и аналогично находились проекции интенсивности цвета под другими углами.

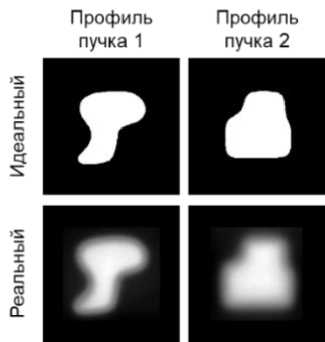
Рис. 2. Тестовые исходные изображения. Белый цвет - 100% интенсивности излучения, черный цвет - 0% интенсивности излучения.

В данной работе для обработки данных использовались программы «Diada» и «INKCT» [21]. Программный пакет «Diada» использует исходные данные в виде матрицы, где каждая строка представляет собой проекцию исходного изображения, общее количество строк - количество углов смещения исходного изображения. Программа представляет исходную матрацу в виде изображения с количеством пикселей, соответствующим количеству значений матрицы, при этом каждый пиксель изображения имеет уровень яркости в градациях серого цвета и соответствует значению, записанному в матрице. Таким образом, в результате обработки получается синограмма. Синограмма сохраняется в формате tif. Данная программа также позволяет проводить обработку полученных графических данных.

Программный пакет «INKCT» позволяет проводить реконструкцию полученных синограмм. Для того, чтобы восстановить данные, необходимо задать угол смещения, размер исходного изображения, центр вращения. Также программа позволяет проводить фильтрацию данных и логарифмическую коррекцию при реконструкции в случае необходимости.

Критерии достоверности реконструированного изображения. Для качественной и количественной оценки достоверности реконструированного изображения в работе использовалось среднеквадратичное отклонение интенсивностей в каждой точке восстановленного изображения от истинного [26-28]. Данный критерий повсеместно применяется в томографических методах, основанных на математической реконструкции. Поиск нормированного среднеквадратичного отклонения осуществлялся по следующей формуле:

• * = J^W/ rec C^y , ) ^- f⁽X_by j))² , ⁽1)

где М и N - размеры изображений в пикселях по горизонтали и вертикали соответственно; f_Tec(x_t,y j ) - значение интенсивности в точке (x_t,y j ) реконструированного изображения; f(x_by j ) - значение интенсивности в точке (x_t,y j ) исходного изображения.

В случае, когда два исследуемых изображения абсолютно одинаковы σ =0, когда абсолютно разные о =1.

Ещё одним критерием для сравнения изображений является евклидово расстояние [29-31]. Данный критерий позволяет количественно различить два изображения. Евклидово расстояние определяется следующим образом: исходное изображение представляется в виде графика статистического распределения элементов цифрового изображения с различной яркостью. Данный график имеет вид гистограммы, на которой по вертикали отложено относительное число пикселей с конкретным значением яркости, а по горизонтали – яркость.

Полученные гистограммы представляются в виде вектора и вычисляется евклидово расстояние по формуле:

• 5 = ^к Ст к -е к )² , (2)

где m k – количество пикселей с яркостью k исходного изображения; e k – количество пикселей с яркостью k реконструированного изображения.

В случае, когда два исследуемых изображения абсолютно одинаковы δ =0; когда абсолютно разные – δ равен корню из общего числа пикселей каждого изображения. Для сопоставления результатов далее в работе все изображения были одинакового размера, равного 500×500 пикселей. Таким образом, максимальное значение δ равно 500.

Также в работе для каждого рассмотренного распределения было определено оптимальное количество проекций ( n опт ) [21]. Оптимальное количество проекций в данном исследовании – такое количество проекций, при котором за минимальное время измерения результат реконструкции будет оставаться достоверным. Данное определение можно описать математически следующим образом: n опт – это точка, в которой скорость возрастания функции совпадения изображений от n (числа проекций) равна скорости возрастания функции времени, затраченного на набор данных, от n . Такой подход к поиску оптимального значения некоторой величины предложен в работе [32]. Таким образом, выражение для определения оптимального количества изображений имеет вид:

• ⁿ опт = J ^-^ (3)

где a – коэффициент линейной функции, которой описывается зависимость времени проведения измерения от количества проекций; b и c – коэффициенты степенной функции, которой достоверно аппроксимируется зависимость полученных значений критериев достоверности восстановленных изображений от количества проекций.

Результаты и обсуждение

В работе были получены реконструированные изображения тестовых распределений электронного пучка для профилей 1 и 2. На рис. 3 и 4 представлены некоторые восстановленные изображения для соответствующих профилей при разных количествах проекций n , полученных с угловым шагом Δϕ .

На рис. 3 и 4: идеальный – полученный на основе расчётов планирующей системы, и реальный – полученный экспериментально. Для всех распределений на рис. 3 и 4 видно, что при количестве проекций, равном 12 и выше, визуально определяется характер исходного распределения. При этом при количестве проекций, равном 6, для реальных профилей пучка характер исходного распределения визуально просматривается лучше, чем для «идеальных». Это может быть связано с особенностями применяемого в работе метода обратного преобразования Радона, который эффективнее восстанавливает изображения, которые в исходном виде не имеют чётких границ и резких переходов от абсолютно чёрного к абсолютно белому цвету.

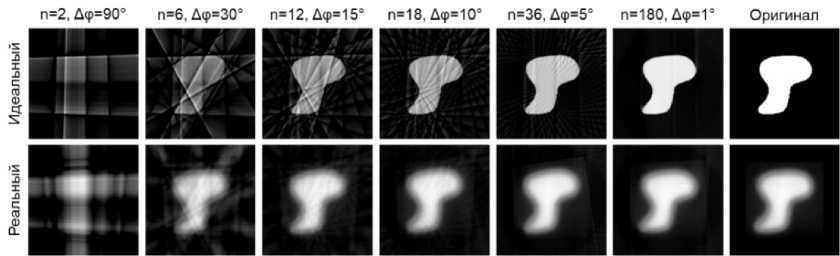
Рис. 3. Результаты реконструкции профилей пучка 1 интегральным преобразованием.

п=2, Дф=90°   n=6, Дф=30°   n=12, Дф=15“ п=18,Дф=10°   п=36. Дф=5°   п=180, Дф=1° Оригинал

Рис. 4. Результаты реконструкции профилей пучка 2 интегральным преобразованием.

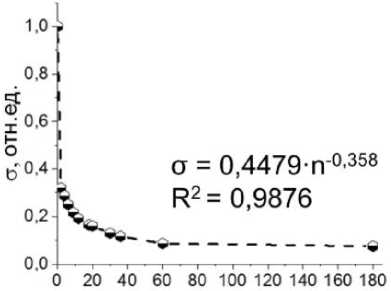
Для количественной оценки полученных результатов были рассчитаны критерии качества реконструкций и оптимальное количество проекций для каждого исходного распределения. Для этого все изображения, представленные на рис. 3 и 4, были преобразованы в виде матриц интенсивностей с одинаковым количеством пикселей, после чего по формулам (1) и (2) были рассчитаны критерии достоверности результатов. На рис. 5 для примера представлена зависимость среднеквадратичного отклонения результатов от количества проекций для расчётного распределения, полученного для «идеального» профиля пучка 1.

п, проекций

Рис. 5. Зависимость среднеквадратичного отклонения реконструированных распределений для «идеального» профиля пучка 1 от количества проекций.

Аналогично результатам, представленным на рис. 5, были получены зависимости и аппроксимационные кривые для обоих критериев и профилей. В табл. 1 представлены коэффициенты для расчёта оптимального количества проекций по формуле (3) для каждого распределения.

Коэффициент a был получен путём определения коэффициента линейного уравнения n(t) , по двум известным координатам: n =0, t =0 и n =180, t =1. Коэффициенты b и c были получены путём аппроксимации степенной функции зависимостей полученных значений критериев достоверности восстановленных изображений от количества проекций [22]. В табл. 1: идеальный – полученный на основе расчётов планирующей системы, и реальный – полученный экспериментально.

Таблица 1

Коэффициенты аппроксимационных уравнений для каждого рассмотренного случая

Коэффициенты Профиль	σ(n)			δ(n)			n опт
	a	b	c	a	b	c
Профиль 1 идеальный	0,056	0,448	-0,358	2,778	223,9	-0,358	11,89
Профиль 1 реальный	0,056	0,240	-0,491	2,778	119,9	-0,491	7,75
Профиль 2 идеальный	0,056	0,378	-0,401	2,778	189,1	-0,401	10,60
Профиль 2 реальный	0,056	0,268	-0,462	2,778	113,9	-0,462	8,35

В табл. 1 оптимальное количество проекций ( n опт ) является расчётным и представлено в дробном виде, однако на практике данное значение должно быть целым и будет округляться в большую сторону. Расчётные данные ( n опт в табл. 1) повторяют результаты визуальной оценки. Для экспериментальных распределений оптимальное количество проекций в обоих случаях ниже, чем для расчётных распределений. Как было отмечено ранее, это связанно с особенностями применяемой математической реконструкции методом обратного преобразования Радона.

В результате работы показано, что метод многоуглового сканирования пучка может быть применён для контроля медицинских электронных пучков. При диагностике поперечных профилей медицинских электронных пучков сложной формы, которые по характеру распределения соответствуют рассмотренным в данной работе случаям, методом многоуглового сканирования достаточно проводить измерения в 12 проекциях для получения достоверных результатов. Данное значение количества проекций было выбрано, так как оно является наибольшим полученным оптимальным количеством проекций для рассмотренных случаев (табл. 1).

Заключение

В данной работе было проведено исследование, направленное на оценку возможности применения метода многоуглового сканирования пучка для контроля профиля терапевтических электронного пучка. Для этого в качестве исходных данных были получены расчётные и экспериментальные распределения интенсивности электронных пучков сложной формы, которые используются для проведения лучевой терапии опухолей кожи головы. Из исходных распределений интенсивности терапевтических электронных пучков были получены их проекции под разными углами, с помощью которых методом обратного преобразования Радона были восстановлены исходные изображения. На основе качественной и количественной оценки полученных результатов было показано, что для достоверной реконструкции распределений интенсивности терапевтических электронных пучков необходимо проводить сканирование пучка в 12 проекциях.

Полученные в статье результаты лягут в основу разработки системы онлайн-мониторинга параметров медицинских электронных пучков, использование которой позволит увеличить точность облучения и, как следствие, снизить риски возникновения постлучевых осложнений.

Работа выполнена при финансовой поддержке гранта Российского научного фонда (проект № 21-79-00252).