Оценка возможности применения подстуживания заготовки для борьбы с неоднородностью деформаций по высоте заготовки

При проведении различных технологических операций ОМД (ковки, прокатки на блюминге или слябинге и других), где обрабатывается заготовка большого размера, может наблюдаться неоднородность пластической деформации, вызванная диссипацией напряжений. В зоне контакта металла с валком достигаются большие напряжения, а по мере удаления от валка в глубину заготовки давление распределяется на все большую и большую площадь, вследствие чего напряжения снижаются. Это явление экспериментально установлено и описано в работах ученых, занимавшихся поперечно-винтовой прокат-

кой труб [1, 2], а также в работах ученых, занимавшихся исследованием прокатки больших заготовок на блюмингах [3–5], где имеется схожее соотношение размеров валков и заготовки. Данное явление описано теоретически и, в частности, представлено в работах [6–8].

В работе [9] для борьбы с неоднородностью деформаций по высоте, вызванной диссипацией напряжений, предлагается применять подстуживание заготовки. Применив подстуживание, мы получим металл с большей температурой в середине стенки и с меньшим сопротивлением деформации, таким

Таблица 1

Исходные данные для моделирования

Материал заготовки 08Х18Н10Т Диаметр D, мм 580 Длина L, мм 1750 Плотность материала [11] p, кг/м3 7900 Теплопроводность материла [11] X, Вт/(м • К) 29 Теплоемкость материла [11] С, Дж/(кг • К) 690 Коэффициент конвективной теплоотдачи между металлом и воздухом [10] а, Вт/(м2 • К) 4,2 Степень черноты стали, е 0,6 Температура материала в момент выдачи из печи T0, °С 1280 Температура окружающей среды Tокp среды, °С 20 r = R : ^dT = «(Токр.среды — T) + 6^(^р.среды — T4 ), t > 0; (5)

^z = I: ^ = “ ( ^Т окр.среды ^{— T} ) '-^ ( ^Т о⁴кр.среды ^{— T 4} ) , t >  0, (6) где a - коэффициент конвективной теплоотдачи; ст - константа Стефана - Больцмана 5,67 ■ 10 ^{- 8} Вт/м² • К⁴; е - степень черноты; Т _{окр среды} - температура окружающей среды.

Для решения задачи использован метод конечных разностей на основе неявной четырехточечной схемы, выбрана равномерная пространственная решетка. Мы выполнили дискретизацию уравнения на основе локальной одномерной схемы А.А. Самарского. Cхема Самарского является абсолютно устойчивой и обладает свойством суммарной аппроксимации [12, 13]. Шаг по времени реализуется в два этапа: сначала в направлении одной координаты r , далее в направление второй координаты z .

r = i ■A r ; i = 1,2, ..., N + 1; r = 0, Г 2 , ..., r_N + 1 ; (7)

z = j ■Az; j = 1,2, ..., K +1; z = 0, z 2, ..., zK+1, (8) где Ar - шаг по пространственной координате r ; Az - шаг по пространственной координате z; i, j – номера индексов, N и K – количество шагов по пространственным координатам r и z соответственно.

Аналогично вводится временная сетка:

t n = n ■т ; n = 1,2, ..., M + 1; t = 0, t 2 , ..., t_M + 1

где т - размер шага по времени; M - количество шагов по времени.

Заменим дифференциальные операторы на их конечно-разностные аналоги [12, 13]:

T 1     ^Т , j , n

d t = i, j, n+2 dt          т

а t

Т

^Т , j , n + 1

T 1

i , j , n +2

а

ar

(

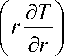
---^ r 1

Ar 2 i+t , j k 2

■ T

i ^{+ 1}>.

- j , ^{n +} 2

—

r

k

i 2,j

^)

+ r 1 ■ ■T 1 + r 1 ■ ■T 1 ■1

i +-, j      I , j , n +-      i —, j    I —1, j , n +

7         2      22

образом мы выравниваем деформации по сечению. В работе [9] заготовка рассматривается как бесконечно длинный цилиндр, и проводится расчет поля температур в зависимо-

сти от расстояния до точки от оси заготовки и от времени. Далее, по полю температур проводится оценка разности механических свойств. Исходя из анализа механических свойств, строится предположение о необходимом времени подстуживания. Однако ничего не гово-

рится о температуре торцов заготовки, их механических свойствах и возможности прошить гильзу, имеющую захоложенные торцы. Для оценки возможности применения подстужива-

ния заготовки мы повторно рассчитали температуру, но уже как функцию двух пространст-

венных координат и времени, т. е. решили уравнение (1) [10]. Для решения задачи ис-

пользовали параметры материала, заготовки и окружающей среды, представленные в табл. 1.

d T X d ( d T A „ d2 T pc — =--1 r— l + X —

В t   r В r V 5 r )    В z

где p - плотность материала; c - теплоемкость металла; X - теплопроводность материала; T – температура тела; t – время; r – координата тела, характеризующая удаленность точки от оси заготовки; z – пространственная координата, характеризующая положение точки по длине заготовки.

Температурное поле будет симметрично относительно оси, относительно середины заготовки по ее длине, и распределение температур будет зеркальным в 4 областях. Поэтому будем вычислять температуры только для одной четверти заготовки.

Мы задались начальными и граничными условиями. Так как время выдержки в печи длительно, то можем считать, что заготовка прогрета равномерно, математически начальные условия запишем следующим образом:

t = 0: T = T , 0 <  r <  — , 0 < z < - ,    (2)

где D – диаметр заготовки; L – длина заготовки.

В середине заготовки на оси и в плоскости, разбивающей заготовку на две половины по длине, из условия симметрии приняли следующие граничные условия:

ВТ r = 0: / = 0, t > 0;                     (3)

В r

ВТ z = 0: '' = 0, t > 0.                        (4)

dz

На поверхности заготовки происходит отвод тепла в окружающую среду конвективной теплоотдачей и излучением. Около поверхности заготовки будет образовываться тонкий слой воздуха, нагретого до температур больших, чем температура окружающей среды. Но так как окружающая среда воздух, а воздух имеет малую вязкость и степень черноты (прозрачен для излучения и практически не излучает тепло), то присутствием тонкого теплого слоя воздуха можно пренебречь, а температуру воздуха в пограничном слое принять равной температуре окружающей среды [10]. Исходя из этого, мы записали граничные условия, для поверхности заготовки используя законы Ньютона – Рихмана и Стефана – Больцмана:

^d T = ^T , j + 1, n + 1 2 ^T , j , n + 1 ^{+ T} , j — 1, n + 1

az2                 Az2, ri—1 j+ rij             rij+ r+1 j                                                   < где r 1 =--------, r 1 = —------, n - шаг по временной координате; n + — - полшага i—2, j         2         i+2, j         2

по времени; ( n + 1 ) - следующий шаг по времени.

Распределение температуры на новом шаге мы определяли согласно уравнениям [12, 13]:

T

I , j , n + —

P^ c---- ²—

t

—

T i, j,n

----= Х

/ Т

i + 1, j , n ⁺ 2

• — 2T    + T /

• i ,    j , ⁿ + 2 i ^— 1, j , ^{n +} 2

* 2 Л

;

k

Т

^Т , j , n + 1

—T

P^ c

т

i , j , n ⁺ 2 = X r i ■ A r²

dr ] T ri + 2 )■ T+1, j, n+1

—

^r. 1 ^{+ r} 1

I — I +

k 2      27

T -, j , n + 1 + r

—

1 ■ T — 1, j , n + 1

.

Полученные системы уравнений сводятся к общему виду [12, 13]:

' Al j.^T      1 — Bl j.^T     1 + Cl j.^T 1 = Fl ij ;

i , j ^{+ 1, n} + 2             i , j , ⁿ + 2             i , j ^— 1, ⁿ + 2

A -T- л ■ .-B -T л+С -Т л ■ , = F

1 ^1 + 1, j,n + 1 U1 i-l, j,n +1 + ^/ i— —1, j,n + 1 il, j , где

Al j =

Д-; Blj =^ + 5c; Clj =

A z ²     j A z ²    т j

^Л - pi = -—T •

; *■ , j               ^Ti , j , n ;

2т

r1                                       r1

A.       "     ; B. = 2L + P C ; C           2'; F = - PCT

A r ²     r i  ’   ¹    A r ²     т ’   ¹    A r ²     r ’   ^z’j       т   i , j , n + 2

Трехточечные уравнения сводятся к двухточечным:

' T i = al j- ^T       i + bl_t j ;

_< ⁱ , j , ^{n +} 2              ⁱ, j ^{+ 1, n +} 2

i , j , n + 1 a l i + 1, j , n + 1 ^{+ U}1 , j ’

где al _j

Alj                Ci " b /-i — F /

----------j -------; bl = ^{j 1} ’ ^j 1 -----^ ; Bl j - Cl j "  al j _{— 1}      ¹ ’ ^j     B j - C j "  a j _{— 1}

ai =

B i

—

A i

C l "  a - — 1,

;

b i, j =

C i " b — 1, j

B i

—

—

F -

, j

C i- a - — 1

.

Для определения a , b ,j и alj , bl ,j по (16) необходимо знать a1 , b ,1, и al1 , bl1, j , которые находим из левых граничных условий: a1 = 1; b 1 = 0; al1 = 1; bl1 j = 0.

Правое граничное условие используется для определения температуры на поверхности:

„ d T л— dr

r = D /2

= afr окр.среды

—

^TN + 1, j ) ⁺ '"'^ ( ^T окр.среды    ^TN + 1, j ) ;

„ d T л— dz

z = L /2

^{a( T} окр.среды    ^Ti, K + 1 ^{) +} ^^ ( ^T окр.среды    ^Ti, K + 1 ) ;

T N + 1, j , n + 1 л--——

—

Ar

T N , j , n + 1

——— = a

окр.среды

—

^TN + 1, j , n + 1 ) ⁺ ^^ ( ^T окр.среды

—

^TN + 1, j , n + 1 ^{) ;}

T 1 — T 1

i, K+1, n +—    i, K, n +— л-------2--------2

л

^{a T} окр.среды

I

—

T i i, K+1, n+-

’     ’ 2 7

(

⁺ ^^ ^T жр.среды I

—

л

T 4      !

i , K + 1, n +- ’     ’ 2 7

.

В системе уравнений (18), используя выражение (16), выполним замену неизвестных T ₁ i , K , n +— ,,   ₂

и T N j n + i , в результате чего получим систему:

Т ] — al " T ] — bl j i, K+1, n +-      j    i, K+1, n+-       , j

Л--------2----------------2-------

Az

A

^{a T} >кр.среды

I

— T

i , K + 1, n + ¹

’     ’ 2 7

(

⁺ ^^ ^T >кр.среды

I

—

T ⁴

i , K + 1,

A

n + 1

2 7

;

^TN + 1, j , n + 1    ^ai " ^TN + 1, j + 1, n + 1    ^bi , j

Ar

окр.среды

—

^TN + 1, j , n + 1 ) ^{+ e}^ ( ^T окр.среды

—

^TN + 1, j , n + 1 ) .

После, рассчитав все прогоночные коэффициенты и температуры на поверхности, мы рассчитывали распределение температур в заготовке на следующем шаге по формуле (16).

Без проведения математических расчетов понятно, что температура торца заготовки будет резко ниже температуры в срединных сечениях. Мы можем уменьшить этот перепад, применяя экранирование при подстуживании. Заготовка транспортируется по рольгангу около 90 с, после чего сваливается на стол перед зацентровщиком. Подстуживание заготовок выполняется именно в этом месте, и установить экраны удобно здесь. Для того чтобы рассчитать температурное поле в заготовке при использовании экранов около торцев, в течение первых 90 с на торце заготовки использовали граничные условия (6), после 90 с граничные условия поменяются, степень черноты материала уменьшится (конечно степень черноты материала останется такой же, но часть тепла, излученного торцем заготовки, будет отражаться от экрана и вновь падать на торец; для упрощения расчетов мы будем считать, что торец имеет меньшую, чем прежде, степень черноты, назовем эту величину условной степенью черноты s * ). Записали граничные условия на торце в математическом виде:

z = L : X^T = a ( Т окр.среды - T ) + sa ( T ₀⁴кр.среды - T ⁴) , t e [ 0;90 ] ;

• ²    ° ^z                                                                               (20)

z = L : X — = a( T„_e- T] + s * ct T⁴  _e  - T ⁴), t >  90.

• 2    d \ окр.среды у у окр.среды у

  Далее мы выразили условную степень черноты торца s * следующим образом. Пусть E – тепловой поток, излучаемый абсолютно черным телом, имеющим такую же температуру, как и торец заготовки. Тогда наше тело излучает s E , экран имеет степень черноты s ₃ и поглощает тепловой поток s ₃ s E , а энергию ( 1 -s ₃ ) s E отражает. Будем считать, что вся отраженная от экрана энергия падает на торец заготовки и поэтому торец заготовки поглотит следующее количество тепла ( 1 -s ₃ ) s E . Таким образом, с торца заготовки излучается тепловой поток s E , и на торец падает тепловой поток ( 1 -s ₃ ) s E , исходя из этого, условная степень черноты определяется формулой [10]:

  s * = s- ( 1 -s ₃ ) s .                         (21)

  На практике могут быть применены экраны из материалов, представленных в табл. 2.

  
  

  На основании данных табл. 2 примем степень черноты экрана равной s ₃ = 0,2. Такая степень черноты является усредненным значением степени черноты различных материалов, используемых в качестве экранов. При таком значении степени черноты экрана условная степень черноты торца равна s * = 0,12.

  Так мы рассчитали температуры в заготовке через 90, 150, 300, 600 с после выдачи из печи (рис. 1–4) при условии использования экранов у торцов и без использования экранов.

  Из термограмм мы видим, что при длительном подстуживании поверхность начинает охлаждаться до температур, ведение процесса при которых становится опасным. После подстуживания в течение 10 мин вся поверхность заготовки имеет температуру порядка 950–1000 °С, что может привести к образованию дефектов поверхности. При этом

  
  

Таблица 2

Степень черноты некоторых материалов, используемых в качестве экранов [14]

Материал	Диапазон температур t , °С	Степень черноты s
Сталь, нержавеющая аустенитного класса	477–1310	0,24–0,31
Алюминий окисленный	200–600	0,11–0,19
Медь слегка полированная	311	0,15
Сталь полированная	500–900	0,27–0,31

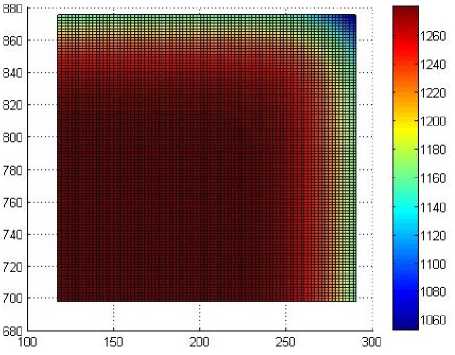
Рис. 1. Температурное поле через 90 с после выдачи из печи

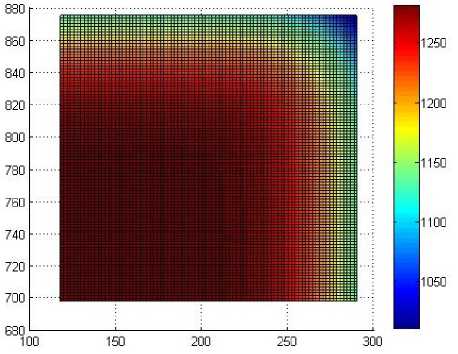
а)

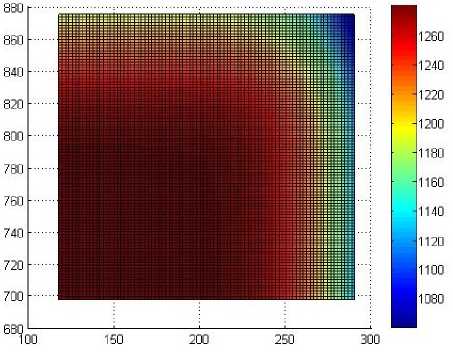
б)

Рис. 2. Температурное поле через 150 с после выдачи из печи: а – без применения экранов; б – с применением экранов

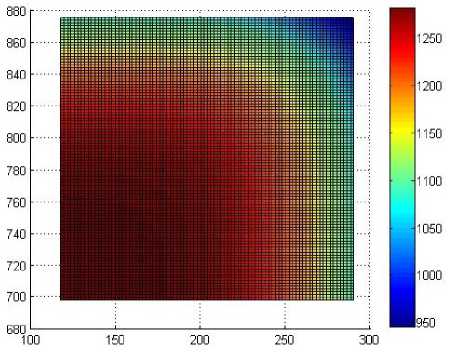
а)

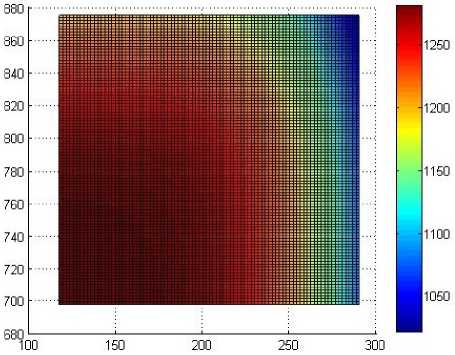
б)

Рис. 3. Температурное поле через 300 с после выдачи из печи: а – без применения экранов; б – с применением экранов

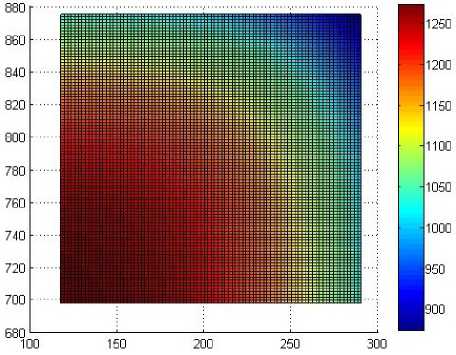
а)

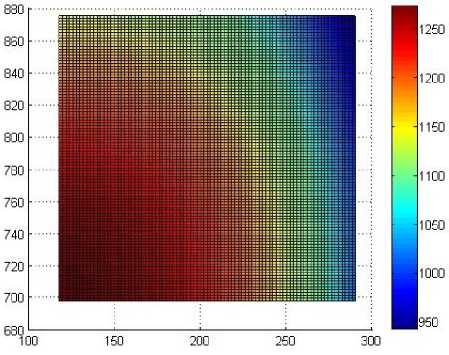
б)

Рис. 4. Температурное поле через 600 с после выдачи из печи: а – без применения экранов; б – с применением экранов

Глубина подстуженного температурного слоя

Таблица 3

Время подстуживания, с 90 120 150 300 600 Глубина слоя, мм 42 52 60 94 146 не происходит проникновения неоднородности температур до середины заготовки. Глубина слоя, где возникает неоднородность механических свойств по причине неоднородности температур в разные моменты времени, представлена в табл. 3.

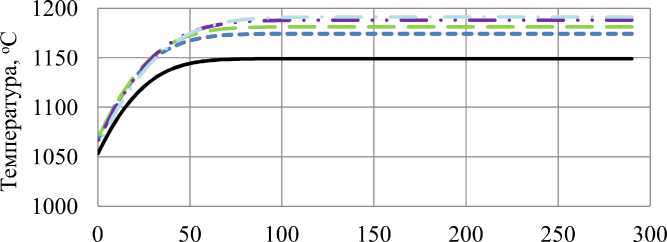
При использовании экранов удается значительно уменьшить захолаживание торцов; в начальный момент времени применения экранирования может даже происходить разогрев поверхности металла или поверхностных слоев за счет передачи тепла центральных слоев, что видно из графиков распределения температуры (рис. 5. и 6). Разогрев поверхности происходит на 40 °С, а разогрев слоев на глубине 5,4 мм – на 25 °С в течение 60 с после

установки экранов, далее разогрев торцов прекращается. Также из графиков на рис. 7 и 8 мы видим, что через 20–30 с замедляется скорость охлаждения слоев на удалении 18 и 45 мм от торца.

Для оценки неоднородности пластических свойств воспользуемся формулой [15]:

a ₅ = K о s д ^{K s} U K U exp ( - K_t • t ) , (22) где s _д - степень деформации; U - скорость деформации; t – температура деформации; K ₀ = 325; K _£д = 0,28; K U = 0,087; K _t =- 0,0028 - эмпирически полученные коэффициенты [14].

Расстояние от поверхности, мм

---90 ---100 --ПО--130      150

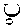
Рис. 5. Распределение температур на торце через 90, 100, 110, 130 и 150 с после выдачи из печи (в момент времени 90 с у торцов заготовки помещены экраны)

^ 1200

й 1150

Он

S 1100

Расстояние от поверхности, мм

----90 ---100 --ПО--130--150

Рис. 6. Распределение температур на глубине 5,4 мм от торца 90, 100, 110, 130 и 150 с после выдачи из печи (в момент времени 90 с у торцов заготовки помещены экраны)

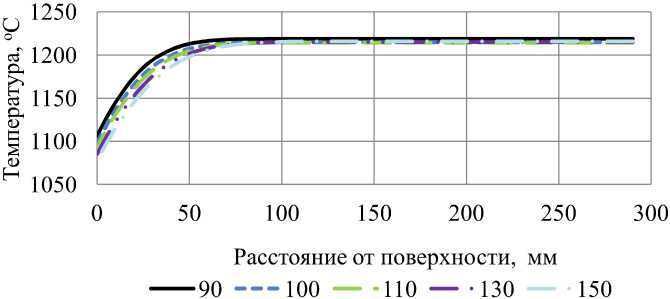
Рис. 7. Распределение температур на глубине 18 мм от торца 90, 100, 110, 130 и 150 с после выдачи из печи (в момент времени 90 с у торцов заготовки помещены экраны)

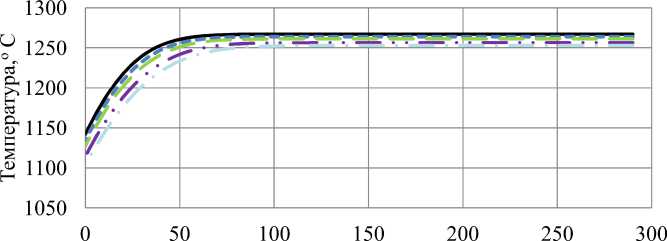
Расстояние от поверхности, мм

----90 ---100 --ПО--130      150

Рис. 8. Распределение температур на глубине 45 мм от торца 90, 100, 110, 130 и 150 с после выдачи из печи (в момент времени 90 с у торцов заготовки помещены экраны)

Так как нам неизвестно поле скорости и степени деформации, оценим разницу механических свойств при вд = const и U = const, т. е. покажем влияние на сопротивление деформации только температуры, выполним это, рассчитав величину (будем называть ее фактор температуры):

K = exp(- K t • t ).                       (23)

Результаты расчета этой величины пред ставлены на диаграммах рис. 9–12.

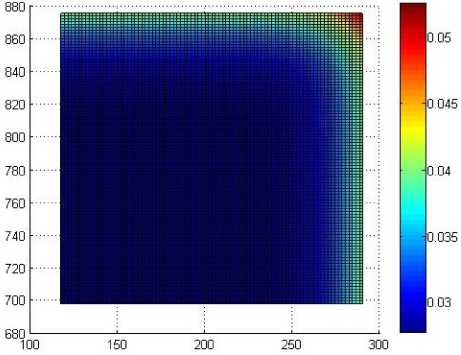
Рис. 9. Распределение функции K ( t ( z , r )) через 90 с после выдачи из печи

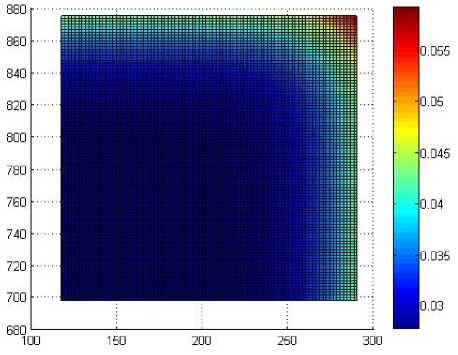
а)

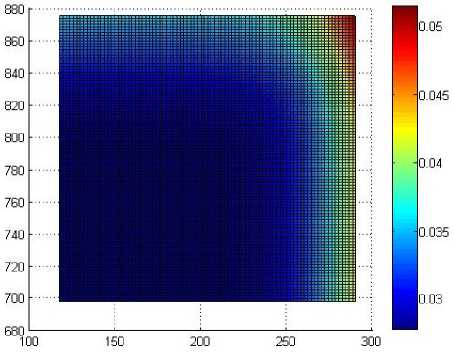
б)

Рис. 10. Распределение функции K ( t ( z , r )) через 150 с после выдачи из печи: а – без использования экранов; б – с использованием экранов

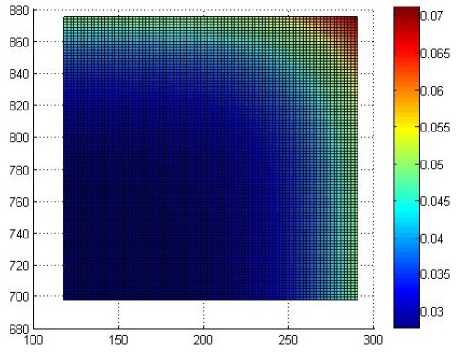
а)

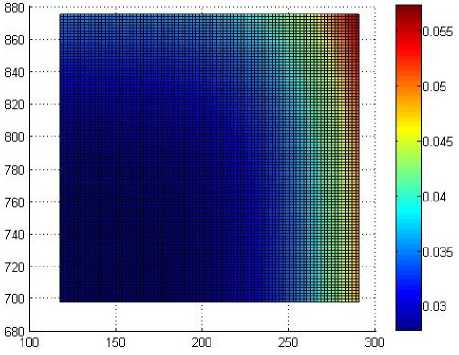
б)

Рис. 11. Распределение функции K ( t ( z , r )) через 300 с после выдачи из печи: а – без использования экранов; б – с использованием экранов

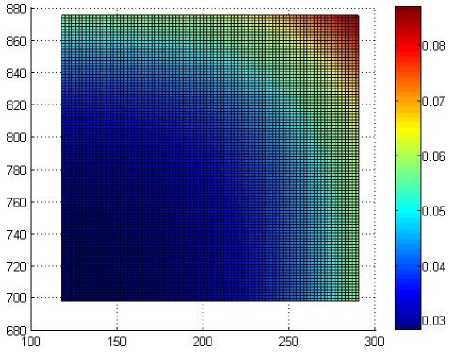
а)

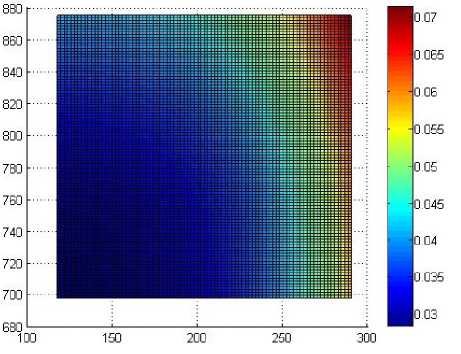
б)

Рис. 12. Распределение функции K ( t ( z , r )) через 600 с после выдачи из печи: а – без использования экранов; б – с использованием экранов

Применяя подстуживание заготовки, можно добиться разницы по значению сопротивления деформации от середины к торцу более чем в 2 раза (при равных скорости и степени деформации), но это неоднородность заключена примерно в слое 100 мм от поверхности, а необходимо распространить ее на всю глубину. Для этого нужно уменьшить тепловой поток, излучающийся с боковой поверхности гильзы, это можно сделать, применив экранирование и на боковой поверхности. Данные расчеты показывают, что основным фактором лимитирующим скорость охлаждения срединных слоев металла является теплопроводность материала, и для получения равномерного перепада температур требуется замедлить теплообмен поверхности и применение подстуживания без применения устройств, замедляющих теплообмен на поверхности, не имеет смысла.