Оценка возможности прогнозирования экстремумов гидрометеорологических параметров с помощью индекса солнечной активности

Наличие тесной связи солнечной активности с гидрометеорологическими и другими природными процессами на Земле является дискуссионной темой. Есть мнение, что не существует высокой и устойчивой корреляции между ними, пригодной для общепланетарного ведения прикладных прогнозных расчетов с высокой достоверностью [1]. В тоже время имеются отдельные успехи в этой области, но они касаются только локальных районов и конкретных природных процессов с привязкой к солнечной активности [2, 3]. Данная ситуация обусловлена большой «зашумленностью» солнечно-земных связей и зависимостью природных процессов от очень большого количества влияющих земных факторов на фоне доминирования нелинейного характера связей между различными событиями. Тем не менее, в ряде исследований зафиксирована достаточно высокая вероятность наступления определенного природного события на конкретном отрезке циклической изменчивости солнечной активности. Это позволяет обратиться к более детальному статистическому анализу корреляционных полей солнечно-земных связей.

Цель работы заключалась в оценке возможности использования метода статистического анализа корреляционных полей, отражающих связь солнечной активности с гидрометеорологическими характеристиками, для прогнозирования их экстремальных значений, которые способны генерировать геоэкологические аномалии.

Под геоэкологическими аномалиями в данной статье авторы подразумевают природные события редкой повторяемости (менее 10%) на поверхности Земли, которые могут повлечь за собой катастрофические последствия для экосистем, её отдельных районов или локальных зон. Этот термин не является стандартным (устоявшимся), но он подчеркивает суть негативного события, которое является не типичным для сложившихся за многие годы связей природных и техногенных (антропогенных) процессов. Здесь необходимо подчеркнуть, что в отсутствие общепринятых количественных критериев величина 10% принята авторами применительно к условиям рассматриваемой задачи.

В первую очередь, это касается гидрометеорологических процессов, способных разрушить различные промышленные объекты или иным способом повлиять на их

И.В. Мискевич, Е.И. Котова

ОЦЕНКА ВОЗМОЖНОСТИ ПРОГНОЗИРОВАНИЯ ЭКСТРЕМУМОВ ГИДРОМЕТЕОРОЛОГИЧЕСКИХ ПАРАМЕТРОВ

С ПОМОЩЬЮ ИНДЕКСА СОЛНЕЧНОЙ АКТИВНОСТИ работу, что, в конечном счете, приводит к масштабному загрязнению окружающей среды и (или) к массовой гибели охраняемых представителей флоры и фауны. Например, аномально жаркое лето в условиях Арктики способно вызвать деформации фундаментов строений на объектах хранения токсических веществ, их разрушение и последующее попадание таких веществ в окружающую среду. Очень высокая величина влагозапаса снежного покрова в сочетании с очень жаркой весной способна вызвать на северных реках паводок, который может затопить территории расположения вышеупомянутых объектов и вызвать высокое загрязнение (до 100 ПДК и более) поверхностных вод. Резкое похолодание температуры воды осенью способно спровоцировать очень быстрое образование льда на портовой акватории и в сочетании со штормовыми условиями негативно повлиять на операции по разгрузке (погрузке) судов, в том числе, повлекшее за собой значительное загрязнение морских вод.

Следует также заметить, что возникновение гидрометеорологических экстремумов редкой повторяемости может вызвать геоэкологические аномалии природного генезиса. К ним, например можно отнести замор лосевых рыб в тундровых реках и озерах при их аномальном прогреве (до 23-25⁰С и выше) в летний период.

При рассмотрении факторов, пригодных для прогнозирования геоэкологических аномалий, сразу обращает на себя внимание солнечная активность. Это параметр, с одной стороны, не зависит от сложных процессов, происходящих в биосфере и геосфере Земли, с другой стороны, активность Солнца полностью определяет возможность существования биосферы нашей планеты [4].

В качестве индикатора солнечной активности обычно применяют числа Вольфа. Это числовой показатель, формируемый количеством солнечных пятен на рассматриваемой звезде. В колебаниях данного параметра наиболее отчетливо выделяется одиннадцатилетний цикл.

В результате анализа его временных рядов установлено, что цикличность солнечной активности является суперпозицией, по крайней мере, трех основных составляющих: 1) одиннадцатилетней (64% дисперсии исходного ряда), 2) вековой (18% дисперсии исходного ряда), 3) квазидвухлетней (11% дисперсии исходного ряда) [5].

Статистический анализ корреляционных полей солнечно-земных связей был использован авторами ранее в работе, посвященной исследованиям зависимости экстремально высоких весенних уровней воды в дельте р. Северная Двина от изменчивости чисел Вольфа [6]. Было выявлено, что максимальная вероятность его появления наблюдается в диапазоне чисел Вольфа 101-125. При более высоких значениях чисел Вольфа наблюдалась линейная тенденция к снижению вероятности появления экстремально высоких уровней до нулевого значения.

В данной статье для того, чтобы оценить возможность использования метода статистического анализа диаграмм рассеяния при прогнозировании геоэкологических аномалий, были проведены расчеты для различных гидрометеорологических параметров в западном секторе российской Арктики.

Материалы и методы

В работе были использованы значения гидрометеорологических параметров в западном секторе российской Арктики, который включает в себя акватории Баренцева, Печорского и Карского морей с прилегающей материковой зоной:

• –    среднее значение температура воздуха в мае на гидрометеостанции (ГМС) Норильск за 1933-2020 гг.,

• –    годовая сумма осадков на ГМС Индига (побережье Баренцева моря) в период 19242020 гг.,

• –    среднее значение температуры воды в октябре на ГМС Унский Маяк в Белом море в период 1975-2008 гг.,

• -    высота снежного покрова в период максимального влаг запаса (март) на ГМС Холмогоры (Архангельская область) ежегодно за 1966-2020 гг.

Данные получены из Государственного фонда данных о состоянии природной среды. Выборка данных проводилась с использованием Web-технологией «Аисори - Удаленный доступ к ЯОД-архивам» ¹ .

Данные по числам Вольфа были получены с использованием ресурсов Геоинформаци-онного портала «МЕТЕО ДВ» ² .

Для анализа данных были построены диаграммы рассеяния для чисел Вольфа и значений гидрометеорологических параметров. Далее на соответствующей диаграмме рассеяния ось чисел Вольфа делилась на равные интервалы, протяженностью 25 единиц, и для каждого такого интервала определялась повторяемость искомого экстремума.

• 1     http://meteo.ru/it/178-aisori

• 2     http://meteo-dv.ru/geospace/averageMonthW

Результаты и обсуждение

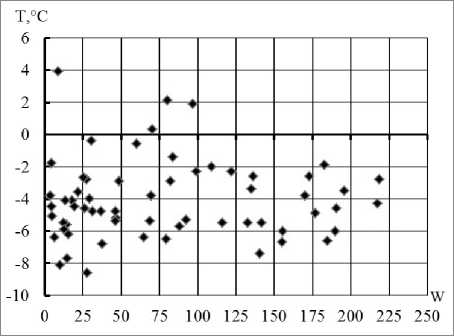
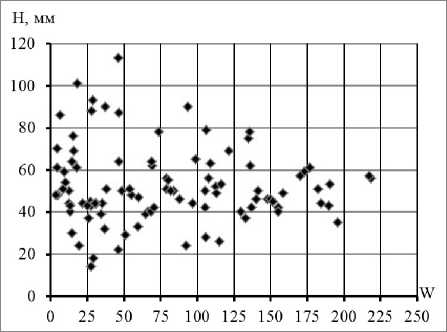
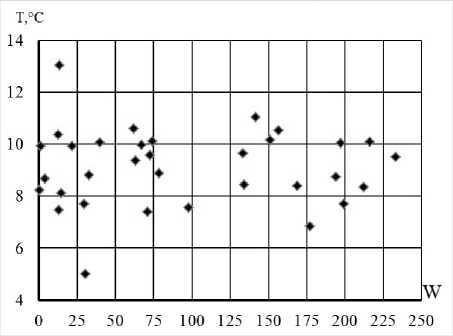
Анализ корреляционных полей многолетних наблюдений (1924-2020 гг.) за различными гидрометеорологическими параметрами на сети станций Росгидромета, включая данные представленные на рис.1, позволяет предположить следующее. Корреляционное поле представлено либо квазитреугольной формой с максимумом дисперсии точек в области низких значений солнечной активности (температура воздуха, годовая сумма осадков), либо сочетанием квазипрямоугольника в диапазоне 0–150 чисел Вольфа (при наличии высокой дисперсией точек) с более коротким треугольником с вершиной на участке 225 и выше чисел Вольфа (температура воды, высота снежного покрова).

a)

b)

c)

d)

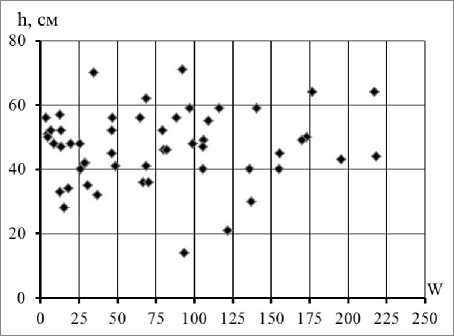
Рисунок 1. Диаграммы рассеяния годовых чисел Вольфа (W) и гидрометеорологических параметров

a) температура воздуха в мае на ГМС Норильск; b) годовая сумма осадков на ГМС Индига в Баренцевом море; c) температура воды в октябре на ГМС Унский Маяк в Белом море; d) высота снежного покрова в марте на ГМС Холмогоры

В ряде ситуаций для треугольных конфигураций корреляционных точек, как и в работе [6], удается получить линейные зависимости их границ, что позволяет рассчитывать (прогнозировать) экстремумы гидрометеорологических параметров для определенной фазы солнечной активности.

В качестве примера можно привести линейные зависимости максимальных сумм годовых осадков на ГМС Индига, расположенной на побережье юго-востока Баренцева моря, и температуры воздуха на ГМС Норильск в мае от значений чисел Вольфа (рис. 2).

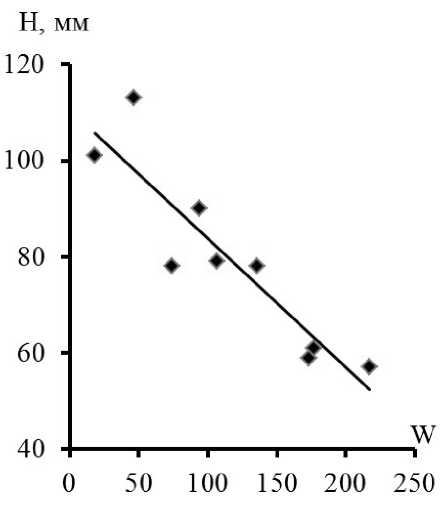
Отметим, что в районе Индиги планируется строительство арктического глубоководного порта, и в годы с аномально высокими атмосферными осадками за счет размыва почвенного покрова и образования обширной микродренажной системы в морские воды может попасть большое количество взвеси и других загрязняющих веществ.

Рассмотрим другой пример. В г. Норильск 29 мая 2020 года в результате аварии произошел разлив большого объема дизельного топлива. Считается, что это И.В. Мискевич, Е.И. Котова

ОЦЕНКА ВОЗМОЖНОСТИ ПРОГНОЗИРОВАНИЯ ЭКСТРЕМУМОВ ГИДРОМЕТЕОРОЛОГИЧЕСКИХ ПАРАМЕТРОВ

С ПОМОЩЬЮ ИНДЕКСА СОЛНЕЧНОЙ АКТИВНОСТИ была одна из крупнейших утечек нефтепродуктов в арктической зоне [7]. Анализ данных показал, что именно в мае 2020 г. здесь была зафиксирована экстремально высокая температура воздуха – + 3,9°С, с повторяемостью 5,9% для интервала чисел Вольфа 0–25 (рис. 1). Высокая температура воздуха, вероятнее всего, обсловила сильное протаивание многолетнемерзлотных пород в рассматриваемом арктическом районе, повлекшее за собой аварийную ситуацию на хранилище дизельного топлива.

а)

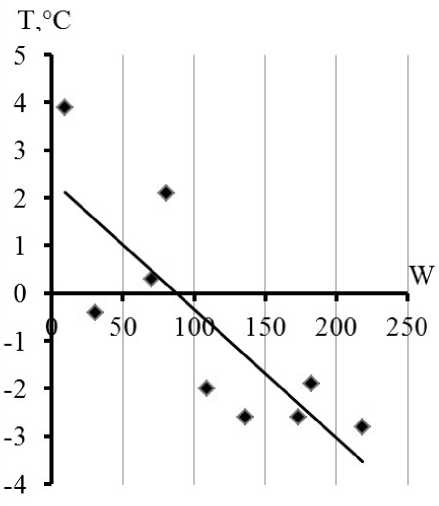
Рисунок 2. Графики связи годовых чисел Вольфа (W)

a) с максимальными температурами воздуха в мае на ГМС Норильск (T, 0C);

b) с максимальной годовой суммой осадков на ГМС Индига (H, mm)

b)

Для определения вышеупомянутых зависимостей воспользуемся стандартной линейной регрессионной моделью, которая имеет следующий вид:

C = A + B x W+ f (e) ₉₅                               (1)

где С – значение исследуемого показателя;

W – значение «управляющего» параметра (число Вольфа),

А и В – константы, определяемые по эмпирическим данным;

f (e) - функция ошибок (регрессионных остатков) 95% обеспеченности, показывающая различия между действительными и расчетными значениями С, которая определяется по следующей формуле:

ε ₉₅ = ±σ_c × t_St × ( 1-R ² ) ^0.5                                      (2)

где σс – среднеквадратичное отклонение для выборки С;

tSt - критерий Стьюдента, зависящий от размера выборки;

R - коэффициент линейной корреляции.

Соответствующие уравнения приведены в таблице 1, их вид показан на рис. 2. Необходимо отметить, что по критериям методического пособия Росгидромета ³ уравнение для максимальных сумм осадков на ГМС Индига в определенных интервалах чисел Вольфа пригодно для ведения прогнозных расчетов.

Для расчета гидрометеорологических экстремумов при наличии нелинейной конфигурации границ диаграммы рассеяния солнечно-земных связей можно использовать одномерные регрессионные модели при предварительной линеаризации таких связей. Последняя операция означает перевод нелинейных зависимостей в квази-

• 3       РД 52.27.759-2011. Наставление по службе прогнозов. Раздел 3. Часть III «Служба морских гидрологических

  прогнозов». М.: ТРИАДА ЛТД, 2011. 194 с.

линейные путем использования элементарных функций, например, при логарифмировании коррелируемых показателей. В этом случае мы получаем возможность более достоверного определения погрешности прогнозных расчетов.

Таблица 1 Регрессионные уравнения для зависимости годовой суммы осадков на ГМС Индига (Н) и температуры воздуха на ГМС Норильск в мае (Т) от годового значения чисел Вольфа (W)

№ п/п	Расчетный показатель	Вид уравнения	Коэффициент корреляции	Коэффициент детерминации	Ошибка расчетов
1	Сумма осадков, мм	H= -0,268W+110,6	– 0,911	0,830	± 18,4
2	Температура воздуха, °С	T= 0,0269W+2,36	– 0,811	0,658	± 3,20

В свою очередь, данные фазу или конкретное число Вольфа можно получить прогнозным расчетом [8, 9], или оценить на основе качественной оценки, учитывая одиннадцатилетнюю доминанту в многолетних колебаниях солнечной активности. В данной статье мы не касаемся гидрометеорологических критериев, способных вызвать конкретные геоэкологические аномалии в западном секторе российской Арктики, т.к. эта проблема требует отдельного рассмотрения.

В качестве первого приближения можно ориентироваться на критерии опасных природных явлений (ОЯ), используемых в системе Росгидромета при составлении гидрометеорологических прогнозов. При отсутствии таковых можно воспользоваться экспертными оценками, методология которых подробно описана в монографии [10].

Выводы

Проведенные исследования показали, что для различных районов западного сектора российской Арктики связь гидрометеорологических параметров, способных нормировать геоэкологические аномалии, с числами Вольфа имеет свой индивидуальный характер. В ряде ситуаций прогнозные экстремумы таких параметров можно рассчитать через одномерные регрессионные модели, учитывающие конфигурацию границ корреляционных полей солнечно-земных связей.

Наиболее высокая вероятность появления геоэкологических аномалий, связанных с гидрометеорологическими экстремумами, наблюдается в диапазоне чисел Вольфа 0–125, при их дальнейшем увеличении она заметно снижается вплоть до нулевого значения.

Для хозяйственной деятельности с наличием рисков возникновения аварийных ситуаций, способных вызвать геоэкологические аномалии («катастрофы»), наиболее «спокойные» годы характерны для периода максимальной солнечной активности, наиболее «тревожные» годы – для периода минимальной солнечной активности.

Рассмотренный подход к прогнозированию геоэкологических аномалий не может претендовать на роль прогнозного метода, соблюдающего соответствующие методические требования Росгидромета. Тем не менее, он может служить дополнительным инструментом для уточнения долгосрочных гидрометеорологических и экологических прогнозов или выступать в качестве альтернативного способа выявления геоэкологических аномалий. Его также можно рекомендовать при ведении проектных работ по строительству промышленных и иных объектов, в том числе, для выбора наиболее «экологически безопасного» периода строительства.