Оценка возмущающего момента при моделировании движения системы наведения антенн

Современные космические средства связи предъявляют всё более и более жесткие требования к функциональным возможностям предоставляемых услуг связи, её непрерывности и готовности, независимо от местонахождения потребителя и времени суток.

Данные функции реализуемы лишь при наличии возможностей оперативного и точного наведения антенн на наземные пункты, международную космическую станцию, космические аппараты, находящиеся на низкой и круговой орбите.

Этим обусловлен переход на использование крупногабаритных антенн и высоких связных частот, что приводит к чрезвычайно жестким требованиями к управлению наведением.

Ввиду жесткого лимита веса и объема космического аппарата созданные большие конструкции антенн являются гибкими в силу выбора легкого материала, а упаковка такой конструкции получается более плотной. Также большие космические конструкции имеют большое количество форм колебаний, которые обладают низкой частотой и близко расположены друг к другу.

В результате антенная система становится более сложным многомерным объектом управления, и это диктует новые требования к системам управления положением антенн.

Необходимость ограничения возмущающего момента на аппарат при соблюдении заявленной точности и скорости сопровождения объекта создала задачу построения системы наведения антенн, не влияющей на ориентацию и стабилизацию космического аппарата при выполнении основной функции.

Конструкция антенны, для управления которой проектировалась система наведения антенн, выполнена из 16 углепластиковых спиц, на которые натянуто радиоотражающее сетеполотно. Антенна в рабочем положении (рис. 1) установлена на штангу.

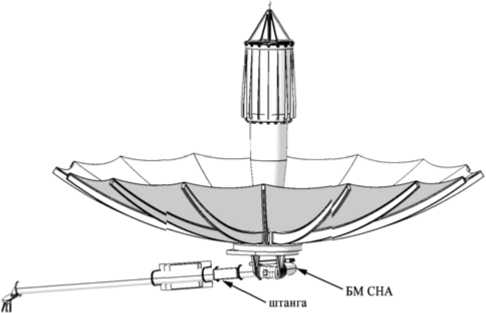
Рис. 1. Общий вид антенны в рабочем положении

На этапе создания системы наведения антенн было уделено внимание оценке возмущающего момента при математическом моделировании работы системы при управлении положением нежесткой антенной.

Моделирование даёт возможность увидеть, как будет вести себя система в действительности. Для получения реальной картины поведения системы была разработана математическая модель, которая учитывает воздействие факторов, оказывающих наибольшее влияние на работу системы.

Электромеханический модуль (ЭММ) блока механического системы наведения антенн (БМ СНА) моделируемой системы наведения антенны состоит из двух параллельных ветвей по пять ступеней, последняя ступень является волновой передачей, связанной с выходным валом. В данной модели представлена только одна из ветвей.

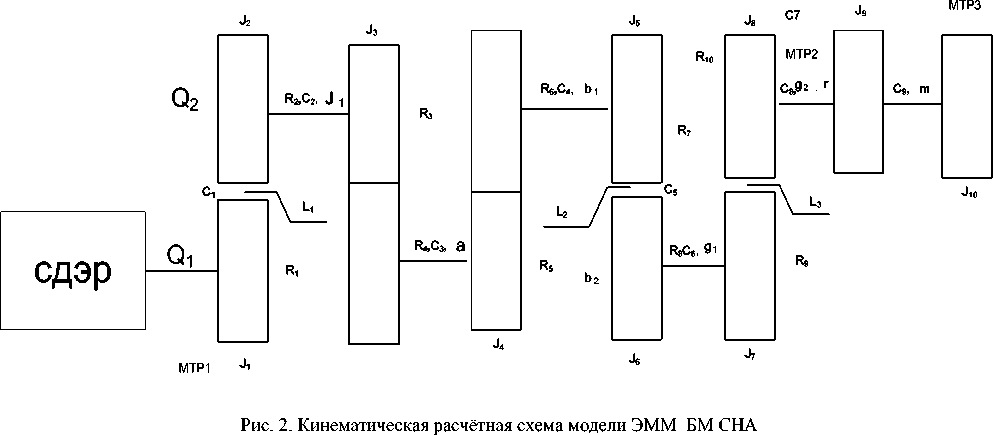
По результатам анализа структуры ЭММ БМ СНА разработана расчётная эквивалентная схема модели. Данная схема представлена в виде кинематической схемы, с учётом нежёсткости и люфтов редуктора и упругости антенны, на рис. 2.

Все ступени редуктора содержат нелинейность типа люфт.

Математическая модель редуктора (рис. 2) с учётом нежёсткости и люфтов представляет собой систему дифференциальных уравнений (2)–(11), представленных ниже.

В уравнениях обозначено:

J ₁ – момент инерции вала синхронного двигателя с электромагнитной редукцией (СДЭР) и первой шестерни редуктора;

AI 1, AI 2, AI 3 – амплитуда тока в соответствующей фазе;

CM 1, CM 2, CM 3 – коэффициенты момента СДЭР для соответствующей фазы;

θ 1 – угол поворота ротора СДЭР и первой шестерни редуктора;

SIN (2∙π∙ F ∙ t ), SIN (2∙π∙ F ∙ t+ 120º), SIN (2∙π∙ F ∙ t- 120º) – синусоидальная форма тока в соответствующей фазе;

SIN (2∙π∙θ 1 ∙ t ), SIN (2∙π∙θ 1 ∙ t+ 120º), SIN (2∙π∙θ 1 ∙ t- 120º) – синусоидальная форма момента СДЭР в соответствующей фазе;

COF 1, COF 2 – коэффициенты, учитывающие вторую и третью гармоники в форме момента СДЭР;

PF 1, PF 2, PF 3 – погрешность сдвига фаз для соответствующей фазы СДЭР;

F – частота тока в фазах двигателя;

KD – коэффициент вязкого трения (коэффициент демпфирования) в СДЭР;

MTP 1 – момент сухого трения на валу СДЭР;

K – коэффициент электромагнитной редукции СДЭР;

• θ₂, ν₁, α, β₁, β₂, υ₁, γ₁, γ₂, ρ – углы поворота соответствующих шестерён в редукторе (рис. 2);

• μ – угол поворота антенны;

• J 2 , J 3 , J 4 , J 5 , J 6 , J 7 , J 8 , J 9 – моменты инерции соответствующих шестерён в редукторе (рис. 2);

J 10 – момент инерции антенны (рис. 2);

R 1, R 2, R 3, R 4, R 5, R 6, R 7, R 8, R 9, R 10 – радиусы соответствующих шестерён в редукторе;

C 2, C 3, C 4, C 6, C 8 – жесткости на кручение соответствующих осей в редукторе (рис. 2);

C 1, C 5, C 7 – упругое сопротивление («твердость») зубцов (первой, четвертой и пятой ступеней редуктора) шестерён при соприкосновении зубцов после выборки люфта;

C 9 – жесткость на кручение выходного вала, в месте крепления антенны к БМ, для моделирования первого тона упругих колебаний антенны;

• L 1, L 2, L 3 – люфты на первой, четвертой и пятой ступенях редуктора (рис. 2);

KD 2, KD 4, KD 6, KD 8 – коэффициенты вязкого трения при демпфировании упругих колебаний в редукторе;

• KD 9 – коэффициент вязкого трения при демпфировании упругих колебаний антенны;

MTP 2 – момент сухого трения на последней (выходной) ступени редуктора;

DX , DY , DZ – относительное линейное перемещение зубьев шестерён соответствующих радиусов;

DXL , DYL , DZL – «проникновение» одного зуба в другой после того, как выберется люфт

DX = θ 1 ∙ R 1+ θ 2 ∙ R 2,                  (1)

если DX < 0, то DXL= DX + L1, при этом, если DXL ≥ 0, то DXL=0, если DX ≥ 0, то DXL = DX – L1, при этом, если DXL ≤ 0, то, DXL = 0 то есть люфт не выбран.

Математическая модель синхронного двигателя с электромагнитной редукцией в виде дифференциальных уравнений имеет следующий вид:

J 1 -9 * 1 = AI 1 - CM 1 - SIN (2 -л- F - t ) х

X [ SIN ( K - 9 1 + PF 1) + COF 1 - SIN (2 - K - 9 1 + PF 1) +

+ COF 2 - SIN (3 - K -9 ! + PF 1) ] + AI 2 - CM 2 х

X SIN (2 - п - F - 1 + 120 ° ) - [ SIN ( K -9 ! + 120 ° + PF 2) +

+ COF 1 - SIN (2 - K -9 ! + 120 ° + PF 2) +

+ COF 2 - SIN (3 - K -9 ! + 120 ° + PF 2) ] + AI 3 - CM 3 х ⁽²⁾

X SIN (2 - п - F - 1 - 120 ° ) - [ SIN ( K -9 ! - 120 ° + PF 3) +

+ COF 1 - SIN (2 - K -9 ! - 120 ° + PF 3) + COF 2 - SIN х

X (3 - K -9 ! - 120 ° + PF 3) ] - KD - 9 * ! -

- DXL - C 1 - R 1 - MTP 1 - SIGN ( 9 ),

J2- 92 =-(92-U1) - C 2 - (9*2-1*1) X х KD2 - DXL - C1- R2,

J -U = ( 9₂-u, ) - C 2 - ( 9*-и, ) - KD 2 -

3 1 v 2      1/ v 2 1x

- ( N 2 -u 1 + a ) - N 2 - C 3 - ( N 2 -U 1 + a ) - N 2 - KD 3,

J 4 - a = - ( N 2 - u 1 + a ) - C 3 - ( N 2 - u * + a ) - KD 3 -

- ( N 3 •a + p ₁) - N 3 - C 4 - ( N 3^+0*) - N 3 - KD 4,

N2 = R 3/R 4, N3 = R 5/R 6,(5)

DY = в1 • R7+ в2 • R8, если DY < 0, то DYL = DY + L2, при этом, если DYL > 0, то DYL = 0;

если DY >  0, то DYL = DY - L 2, при этом, если DYL < 0, то, DYL = 0.

J 5 -p * =- ( N 3 -a + p 1 ) - C 4 + ( N 3 ^p’ ) х X KD 4 - DYL - C 5 - R 7;

J 6 -p * =- DYL - C 5 - R 8 -                  (7)

- ( P 2 -Y 1 ) - C 6 - ( p * 2 -у* ) - KD 6;

DZ = Y 1 • R 9 + Y 2 • R 10,

если DZ < 0, то DZL = DZ + L3, при этом, если DZL > 0, то DZL = 0, если DZ > 0, то DZL = DZ - L3, при этом, если DZL < 0, то, DZL = 0.

J 7 -y ! = ( ₽ 2 -Y 1 ) - C 6 + (£ -Y 1 ) X           ₍₈₎

X KD 6 - DZL - C 7 - R 9,

J 8 -Y * 2 = ( P-Y 2 ) - C 8 + ( p-Y ₂) - KD 8 -- DZL - C 7 - R 10 - MTP 2 - SIGN ( y * ₂), J 9 - P = - ( P-Y 2 ) - C 8 - ( P- y * 2 ) - KD 8 +

+ ( ц-p ) - C 9 + ( ц-p ) - KD 9,

J10 •ц = -(ц-p) - C 9 - (ц-p) x x KD9 - MTP3 - SIGN(ц).

В блоке управления системы наведения антенны реализована импульсная форма. При импульсной форме тока в фазах двигатель работает в шаговом режиме. Период тока T разделен на шесть частей, средняя величина в радианах определяется по формуле:

⁹ 1 Ш

2 -п

6 K ’

Средняя угловая скорость вычисляется по формуле:

* _ 2-п- F

⁹ СР = K

.

Передаточное число примененного редуктора

R 2 R 4 R 6 R 8 R 10

i =  ⋅⋅⋅⋅   = 10809.

^Р R 1 R 3 R 5 R 7 R 9

С учетом параметров редуктора были определены собственные частоты колебаний ступеней редуктора с учётом нежесткости на кручение [1, с. 305]:

ω= С J ^И                 (14)

102,6 Гц, 127,11 Гц, 103,4 Гц, 12,08 Гц, 20,4 Гц.

На основе проведенного модального анализа антенны в рабочем положении на штанге было получено значение частоты первого тона собственных колебаний антенны 0,83 Гц.

Максимально возможный момент инерции антенны составляет: J ₁₀ = 50 кг ⋅ м² .

При проектировании системы были задано следующее ограничение по работе системы: во всем диапазоне скоростей не должен создаваться возмущающий момент более 0,02 Н ⋅ м (200 гс ⋅ см), в диапазоне частот 0,1–1 Гц амплитуда периодической составляющей возмущающего момента должна быть не более 0,001 Н ⋅ м (10 гс ⋅ см).

Для оценки возмущающего момента, действующего на космический аппарат при работе системы наве- дения антенн, рассматривались несколько вариантов. Данные варианты приведены в таблице.

Возмущающий момент определяется как произведение углового ускорения на момент инерции нагрузки, приведённый к выходному валу ЭММ БМ СНА. То есть оценка возмущающего момента при движении БМ СНА производилась относительно места закрепления на элементе конструкции спутника.

По результатам проведенного моделирования движения антенны для оценки возмущающего момента от БМ СНА использовалась формула:

M _ВМ = J _Н   .

dt

Для построения амплитудно-частотных характеристик колебаний скорости и возмущающих моментов использовалась программная среда Matlab, функция fft [2, с. 138], реализующая алгоритм быстрого преобразования Фурье.

Для оценки возмущающего момента, действующего на космический аппарат (в данном случае при работе СНА в режиме программного наведения), рассматривался диапазон частот 0,1–1 Гц. Для вариантов расчётов были получены частотные спектры возмущающего момента. По результатам анализа проведённых расчётов и полученных частотных спектров были определены максимальные амплитуды возмущающего момента и соответствующие им частоты, которые приведены в таблице.

Возмущающий момент немного более 0,02 Н ⋅ м (200 гс ⋅ см) присутствует в вариантах расчётов 7, 8, 10.

Проведённая оценка по результатам моделирования работы системы показала:

• - величина полученных возмущающих моментов не превышает 0,02 Н·м в диапазоне частот 0,1–1,0 Гц во всей временной области;

  – наблюдаемые возмущающие моменты не корел-лируются с частотами управления, а определяются параметрами зубчатых пар редуктора и выходной ступени.

В результате проведенной работы была получена математическая модель системы наведения антенны, позволяющая моделировать динамические процессы, возникающие в ней, а так же производить оценку возможных возмущающих моментов, которые могут создаваться при её работе. Данные результаты могут быть использованы для оценки динамических процессов на космическом аппарате в целом и оценки влияния на его точность ориентации и ориентацию в пространстве антенны при наведении на наземные пункты, международную космическую станцию, космические аппараты, находящиеся на низкой и круговой орбите.

Максимальные амплитуды возмущающего момента и соответствующие им частоты

№ варианта	α ЦУ,'	а ЦУ ,'/ c	Частота 1, Гц	Момент 1, Н×м	Частота 2, Гц	Момент 2, Н×м
1	50	0,2	0,409	0,0142	0,247	0,0104
2	50	0,5	0,1698	0,0184	0,3196	0,0135
3	50	–0,2	0,368	0,01	0,667	0,00856
4	50	–0,5	0,0499	0,0190	0,29	0,0143
5	150	0,2	0,4489	0,0133	0,92	0,0159
6	150	0,5	0,066	0,0191	0,332	0,0105
7	150	–0,2	0,227	0,0293	0,399	0,0194
8	150	–0,5	0,06	0,0223	0,238	0,0209
9	400	0	0,078	0,0104	0,306	0,0103
10	500	0,5	0,829	0,0388	0,889	0,0139
11	0	0,5	0,83	0,0213	0,76	0,0148
12	10	–0,5	0,648	0,0106	0,282	0,00856

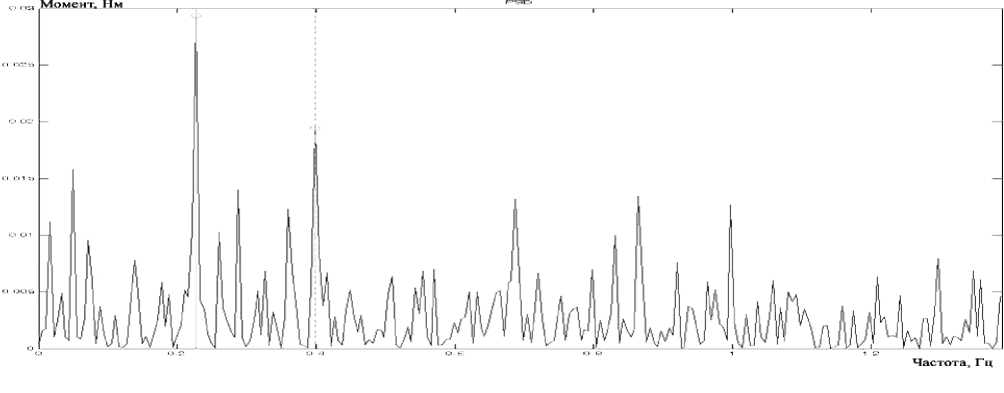
Рис. 3.Частотный спектр возмущающего момента на выходе редуктора (вариант 8)

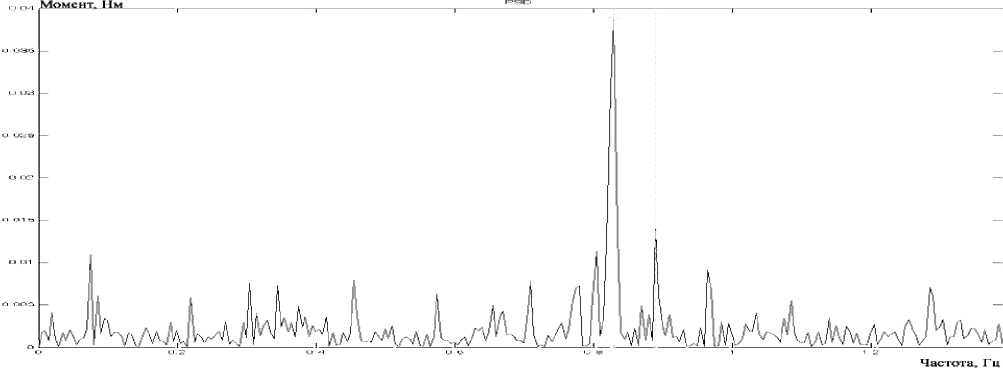
Рис. 4. Частотный спектр возмущающего момента на выходе редуктора (вариант 10)