Оценки чисел Гильберта операторов Харди-Стеклова

В работе исследовано асимптотическое поведение чисел Гильберта интегральных операторов Харди-Стеклова, действующих в пространствах Лебега из L^p в L ^q при 1 <  p , q < да на полуоси. Оператор Харди-Стеклова

И x )

^{Hf (} x ) = v ⁽ x ) j u ⁽ y ) ^{f (} у ) dy .

Ф ( x )

В настоящей статье рассматривается в случае, когда пределы интегрирования ф(х^ и 1(х) удовлетворяют следующим условиям:

• 1)    функции ф(х^ и 1(х) дифференцируемые и строго возрастают на (0, да);

• 2) ф(0) = 1(0) = 0, ф(х^ < 1(х) для

х > 0, ф(да) = 1(да) = да.

В статьях [1-2] ранее были получены результаты для аппроксимативных и энтропийных чисел операторов Харди, которые будут использоваться для получения оценок на числа Гильберта.

Пусть В ( X , Y ) - пространство всех

ствующих из банахова пространства X в банахово пространство Y . Энтропийные числа e_n ( T ) , n G N , (e - числа) оператора T g В ( X , Y ) , определяются как точная нижняя грань множества всех чисел £ >  0 , для которых существуют эле-

V            П 1

менты У 1 , ^ , у_т G Y , где т S 2

m такие, что T(Вх ) с ^ {у^ + гВу } , i=1

линейных, ограниченных операторов дей-

то есть

en ( T ) = inf <  £ >  0 : Я у1

— v      п П —1

Ут g Y, m ^ 2

m

T ( Вх ) с U { yi + £ B y } - , i = 1

где B_x = { x е X : Ц х Ц^ <  1} - единичный шар в X , а By - единичный шар в Y .

Энтропийные числа обладают следующими свойствами: для операторов S , T е B ( X , Y ) и R е B ( Y , Z )

• (i)    T il = e i (T ) >  e 2 ( T ) > ... >  0;

• ⁽ⁱⁱ⁾   e n + m - i ( T + S ) <  e n (T ) + e m (S ),   n , m е N ;                         ⁽¹⁾

• (iii)    e n + m — 1 ( RT ) <  e n (T ) • e m ( R ),   n , m е N .

Энтропийные числа тесно связаны с аппроксимативными числами и числами Гильберта линейных ограниченных операторов.

Приведем следующие определения: n -e аппроксимативное число оператора

T е B (X, Y )

an (T) = inf { ||T — L||^у : L : X ^ Y’ rankL < n } n е N, где rankL = dimR(L);

n -e число Гильберта оператора T е B(X, Y) задается по формуле hn(T) = sup{ an(FTE) : E е B (f 2 ,X), F е B (Y, f 2 ), ||E|| < 1, F\|< 1}

Соотношения между указанными числами содержатся в следующей теореме.

Теорема 1. [3, с. 184], [4, с. 294]. Пусть T е B ( X Y ) . Тогда

• (i)   hn(T) < 2en(T), hn(T) < an(T);(ii)    sup na en(T) < Ca sup na an(T), для любого a > 0.

n

n

Пусть 1 <  p <  " . Обозначим L p (R ⁺ ) пространство Лебега всех измеримых функций с конечной нормой

II fllLp(R+) =

f "

j I f(x)\p dx 10

Л

1 ^p

.

Определим операторы S : L p ( R ⁺ ) ^ L q ( R ⁺ ) при 1 <  p , q <^

у(к>

Sf^c) = v(x) j u(y)f (y)dy,                      (2)

и K : L p ( R ⁺ ) ^ L q ( R ⁺ ) при 1 <  p , q <"

Kf ( x ) = v ( x ) J u ( y ) f ( y ) dy , ^ ( x )

где

весовые

функции

^{u (} y ) ^{g L}p' ^{( R +} ), v ^{( x} ) ^g L q ^{( R +} ) и пределы интегрирования p ( x ), y ( x ) - возрастающие дифференцируемые функции такие, что p (0) = 0, y (0) = 0,

ф (x ) < y ( x ) для x g (0, да ) и у ( да ) = у ( да ) = да .

Критерии об ограниченности и компактности операторов (2) и (3) содержатся в следующей теореме.

Теорема 2. Пусть 1 <  p <  q < да . Тогда

(а1) Оператор S ограничен из L p (R ⁺ ) в L q (R ⁺ ) тогда и только тогда, когда

^Л ^ ⁽ t )           , ^Л

A 1 = ^suP Ay ⁽ t ) = sup j I u ⁽ y ) I ^p dy

t > 0

t > 0 к о причем S

P'

rда,      „ j | v(x )| ddx к t

A

L p ( R ⁺ ) ^ L q ( R ⁺ ) “ A ¹ '

q

< да,

Оператор S : L p ( R ⁺ ) ^ L q ( R ⁺ ) компактен в том и только в том случае, если A 1 <да и lim A y ( t ) = lim A _y ( t ) = 0.

(а2) Оператор K ограничен из L_p(R ⁺ ) в L_q(R ⁺ ) тогда и только тогда, когда

r да

A

Гt

A 2 = sup Ap ⁽ t ) = sup j| u ⁽ y ) ^p dy j| v ⁽ x ) q dx

t > 0

t > ^o u t )

к 0

A

q

< да ,

^причем ||^K| L_p ( R ⁺ ) ^ L_q ( R ⁺ ) »

Оператор K : L p ( R ⁺ ) ^ L q ( R ⁺ ) компактен в том и только в том случае, если

A 2 <да и lim Л _ф ( t ) = lim Л _ф ( t ) = 0. t ^ 0        t ^да

—

—. Тогда ^p

Пусть 1 <  q <  p < да , - = —

sq

(b1) Если оператор S ограничен из L p (R ⁺ ) в L q (R ⁺ ) , то

r да ГУ(x)        ,   )

A =j j |u(t)lp dt

s

P ‘

( да

A

s - 1 ^q

A

| v ( x )| dx

0 к 0 к

к x

s

< да,

кроме того, Hl_P( ( R + ) ^ _L q ( R + ) * ^D 1 .

Оператор S : L p (R ⁺ ) ^ L q ( R ⁺ ) компактен в том и только в том случае, если D y <да .

(Ь2) Если оператор K ограничен из L p (R + ) в L q (R + ) , то

Г

s

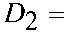
да f 0

да

А

p'

( x

а

s

q

— 1

| v ( x ) | dx

s

< да,

ы x)

V о

V

кроме того, K I L p ( R + ) ^ L_q ( R + ) * ^D 2 -

Оператор K : L p ( R ⁺ ) ^ L q ( R ⁺ ) компактен в том и только в том случае, если D 2 < да .

Доказательство теоремы следует заменой переменных из известных результатов об ограниченности и компактности оператора Харди (см., например, [5, с. 41] § 1.3).

Введем следующие обозначения: для интегрального оператора

S : L p ( R ⁺ ) ^ L q ( R + ) пусть последовательность { ^ n }_ПЕ^ задана формулой

^ ⁽ ^ n )

и( y ( § n )) =   f | u ( t )| ^p dt = 2 ⁿ ,   —да< n < N _v <да .

Определим

^CT n = । u L p ■ ( _V ( 5 _n ), ^ ( ^ „ + 1 )) 11 v I L q ( # „ , 6 ,+ 1 )

и положим

(       ^

r

~ n

V n g Z 7

nr

r

Z 2 ^p ' n g Z

r )

( 6n+1           ) q f |v (x )| qdx

V 6,              7

r

V7

ZII u 1 Г

VneZ    Lp ' ⁽ ^ ( 6n)»(6n + 1))

vr

^L q ^{( 6} n , ⁶ n + 1 )

Г

• 1      1     1

где - = — + -.

^r   p   q

Аналогично, для интегрального оператора K : Lp (R + ) ^Lq (R + ) зададим последовательность {тп }ne2 следующим равенством

U УТ )) =   f | u ( t )| ^p'dt = 2 ^- n , -ro< N _y <  n ,

V ^{( T} n )

положим

^K n

II ^u I Lp - ⁽ ^ ⁽ T n X ^ ( T n +1 )) 11 ^v II L q ^{( T} n , ^T n +1 )

и

г       ^

Z K r

V n е Z  7

r

г

V II u L Z Z X z xx V || и ^L _p ‘ ⁽ ф ⁽ т X ф ⁽т+ i))^{11  11}

V n е Z

r

r

^L q ^{( T} n , ^T n + 1 )

Теорема 3. Предположим, что весовые функции u ( y ) е L p ‘ ( R ⁺ ), v ( x ) е L q ( R ⁺ ), 1

да, такие, что операторы S : Lp (R⁺) ^Lq(R⁺) и K : Lp (R⁺) ^Lq (R⁺) определенные формулами (2), (3) компактны.

• (1)    Пусть А = (a,b) с R⁺, J = (^(a),^(b)), I = (у(a),у(b)), S: Lp (J) ^Lq (А), K: Lp (J) ^Lq (А) . Тогда выполняются следующие оценки:

  
  

x 1/r r с1(p,q) J|u(^(x))|rv(x)|r (^,(х))p dx

< liminf n en (S) < n ^ro

А

V                                7

x 1/r r i

А

V

и x 1/r r i

^с1⁽p, q) J |^u(ф^(x))|^r v(^x)|^r (У⁽х))^{p dx}

а

V7

< liminf n e_n (K) < n ^v

x 1/r

r 1

<limsup nen(K) < c2(p,q) j|u(ф(x))|r\v(x)|^r(^(x))^pdx .

n ^ro

A

V

^с1⁽P, q)

(2) Пусть   £ СТ n

1/r

ro ji uM(x»i v(x)i (^,(х))p dx

0 V

< liminf n en (A) < n ^ro

1/r

ГО

x

V7

и

ro

x 1/r r 1

с1⁽p, q) j | u⁽ф⁽.x))|^r v⁽x)|^{r (}^⁽х))^p dx

о

V                               7

< liminf n en (K) < n ^ro

"ro

q) j u(^(x))r v(x)|r (фХx))p dx n ^ro

V7

1/r

Доказательство. Заменой переменной y = y(t) получаем

^( x)                 x sf(x) = v(x) j u(y)f (y) dy = v(x)j u(Mt))f (Иt)) ^'(t)dt• о                   0

Отсюда следует, что оператор S = Q о ^ является суперпозицией метрического изоморфизма

Т: Lp (R⁺) ^Lq (R⁺), Т:.f (t) ^ f (m(t))M'(t)]^1Zp

и оператора Q : Lp (R⁺) ^L q (R⁺)

x

Qg (x) = v (x) j Uy (t) g (t) dt, 0

.fzp 1/ p где u^ (t) = u(^(t)) [^Xt)]  ^ ■ В силу свойств е — чисел (1) имеем en (5) < M "en (Q) , а также en (Q) < ^

—1

• en (5).

Поскольку ll^ll _{T    T} = ^

^Lp ^ ^Lp

-1

= 1, то en (5) = en (Q). ^Lp ^ Lp

Поэтому, используя результаты [2, с. 36] (теоремы 4.6, 4.10), получаем требуемые оценки. Асимптотические оценки для оператора K выводятся аналогично заменой у = ф(t) .

Следствие 1. Предположим, что весовые функции u(у) e Lp‘ (R⁺),

v^(x) ^eLq⁽R + ), 1< p, q < да, такие, что операторы 5 : Lp (R⁺) ^Lq (R⁺) и

K : Lp (R⁺) ^Lq (R⁺) определенные формулами (2), (3) компактны и ^~n < ro, n e Z

r

Kn< ro. Тогда neZ

\ 1/r r 1

го limsup nhn(5) < c(p,q) J|u(^(x))|r\v(x)|r (^Xx))p dx

,

n ^ГО

к

ro

J

\ 1/r

r 1

limsup nhn (K) < c (p, q) J| u (ф( x ))|^r|v (x )|r (фХ x))^pdx

■

n Vro

к

J

Далее рассмотрим интегральный оператор Харди-СтекловаH : Lp (R⁺) ^Lq (R⁺) с переменной областью интегрирования вида

^( x )

Нf (x) = v(x)  J u (у) f (у) dy■     (4)

^⁽x )

Для исследований асимптотики е-чисел и чисел Гильберта оператора (4) построим специальное разбиение полуоси (0, го) = ^А к, где A = [^k ,^к+i] и к

5k = [nk, Пк+1] определяются для k e Z следующим образом:

Zo = 1,  ПО = Ф(1),  П1 = V(1),  Zk+1 = ⁽Ф^{1 o}V)к (1), k^eZ,

Пк = V(Ф¹o V)k 1, к e Z•

Используя асимптотические оценки аппроксимативных чисел оператора (4), полученные в работе [1, с. 180], оценки теоремы 1 (ii), получаем оценки для энтропийных чисел и чисел Гильберта оператора Харди-Стеклова

H с переменными пределами интегрирования.

Пусть последовательности

{й, n )^eAк и кк, n l^eAк

заданы следующими соотношениями:

^V(^^k,ⁿ)        ,             Ф⁽Ск+1)

J    I u (t)|^p dt = 2 ⁿ,       J | u (t)|^p dt = 2 ^-n.

v(Zk)

Ф^(тк, n )

Определим

^к, n =

^(Zk, n)        ,

J l«⁽t)l pdt

I v(Zk)

p  ък, n+1

J | v ( x )| ^qdx _к^к, n

к

^{и    К}к, n

Ф^к, n )       ,

J    | u (t)|p dt к Ф«к )

к

P '(к, , n + 1

1 ^q

к

J IV⁽x ) l^dx к ^Тк,n              7

1 ^q

•

Теорема 4. Пусть 1 < p < да, оператор H : Lp (R⁺) ^L p (R⁺) компактен и zz ^к n< да,   zz^t, _n< да. Тогда выполняются следующие оценки:

kn       kn

да

limsup nen n ^да

(H) < C⁽p) J|v⁽x)| u⁽ф⁽x^(фХx))^p + u⁽v⁽x⁾⁾|⁽v'⁽x))

dx,

к

да

limsup nhn (H) < С1⁽p) J|v⁽x) u⁽ф⁽x^(фХx))^p + u(v⁽x^(vXx))

P1

dx,

n ^да

к

где C(p), C(p) - некоторые положительные константы, зависящие только от p.

Используя теорему 1 и результаты [3, с. 194], получаем оценки чисел Гильберта для диагональных операторов.

Следствие 2. Пусть диагональный оператор D : £ 2 (R⁺) ^^2 (R⁺) таков, что D⁽^n ) = ⁽^n^n X и<4 ^ ^2 ^ ^3 ^ - ^ ⁰. Тогда

(^       )

Xhn(D )a

V 1           J

(”

^ Pa XI ^Gn

V1

для 0 < a <^,

J

где Pa - некоторая положительная константа.