Оценки исключительных множеств для меры

Уточнённый порядок играет важную роль в теории роста субгармонических функции, в ряде других разделов математики.

Абсолютно непрерывная функция Л. на полуоси л л называется уточнённым порядком, если выполняются следующие два условия :

• 1)    существует предел 7—f+tz                         ,

hm г hirp'fr ) = О

• 2)                   .

В приложениях чаще всего используется не сам уточнённый порядок

Л-’. , а функ-ция

. Отметим следующее свойство уточнённого порядка.

Теорема 1. для любого г > о существует предел

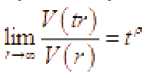
и этот предел равномерный на любом сегменте

Если Л’. – уточнённый порядок, то существует дифференцируемый, и даже анали-тический, уточнённый порядок Р. С’. такой, что

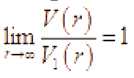
’I '

где            .

Поэтому предположение о дифференцируемости уточнённого порядка часто не ограничивает общности рассуждений. В дальнейшем мы будем предполагать, что функ-ция Л’. является непрерывно дифференцируемой на полуоси .

Рост произвольной функции л?. сравнивается с ростом функции вида

Множество функций вида множество степеней Г , а

– это более широкое множество, чем , или множество функций вида

, где – вещественные числа, а – это -тая итерация логарифма. Например,         .

Пусть Лн

– положительная функция на полуоси

. Порядком

функции называется число

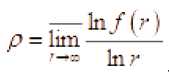
Важность понятия уточнённого порядка в теории роста функций можно усмотреть из следующей теоремы.

Положительная на полуоси функция называется регулярно меняющейся в смысле Караматы, если для любого существует конечный предел

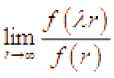
Пусть р (t) - некоторый уточнённый порядок. На пространстве Rc определяется одно-параметрическое семейство преобразований Азарина At: RR ' Rc, t е (0,ж), согласно формулам p (tE) pt Atp’pt(E) v(t) ’

Для любого борелевского множества E .

Пусть ф е Ф ( R о ) . Формула переменных даёт

J ф ⁽ x ) dp_t ⁽ x )= 1^ / ф ( x ) dp ⁽ t )• ^{( 4}-1)

R О                       V ⁽ t ) R 0 t

В этом разделе излагаются технические результаты, которые используются в следующем разделе.

Мы начнём с построения и оценок исключительного множества для меры.

Пусть р (r )-^уточнённый порядок, p -^положительная мера на Rn, п — фиксир-ованное строго положительное число. Обозначим через Eη множество тех точек, || x || > 2, для которых существует число а е(0,2 ] такое, что p ^

Множество ^E η

мы будем называть исключительным для меры μ . Это

название оправдывается тем, что при x£ E^x^ 0 , и

а е(0 ■1

выполняется

неравенство p ^

Покажем, что для каждого x ^е E_n существует а е ( 0 , ¹ ] , для которого выполняется неравенство

наибольшее из чисел

• (5.1).    Пусть A ( x ) -L

множество тех чисел ае (0,1 ], для которых выполняются неравенство (5.1), ax = A(x U, тогда существует последователь-ность вт такая, что вт g( 0 ,ax ] nA (x), lim вт=ax. Имеем m→∞

P L

Это означает, что a_x g a ( x ) и нужное нам утверждение доказано.

Заметим, что если a x <  ^ , то в неравенстве (5.1) будет иметь место знак равенства.

Обозначим

G n = x ^G E n C ( ^x,ax II x II) .

Очевидно, что E n ^c G n и что G n -^ открытое множество. Поэтому представляется в виде не более, чем счётного объединения связных компонент.

G n = iG i .

Набор открытых шаров ^C 1 ,…, ^C m , m≥ 1 , назовём цепочкой, если пересекаются замыкания соседних шаров и только они. Кроме того, если ^{x g} c i , У ^g C m , то говорим, что цепочка соединяет точки x и у .

Теорема 2. Если точки x и y лежат в одной компоненте ^Gi множества ^Gη , то эти точки можно соединить цепочкой шаров вида C ( x_s,a_s || x_s ||) , s = 1,2 ,...,m , где ^x s ^g E n ^nG i .

Доказательство. Пусть H— множество точек, которые можно соединить цепочкой шаров указанного выше вида с фиксированной ^{x g} Gi. Очевидно, что H -^ открытное множество. Докажем, что H— замкнутое множество в относительной топологии компоненты ^G i . Пусть У ^g G i является предельной для точек y_m ^g H , и пусть y g C ( h,a I h ||) = C , где ^{h g} E n . Тогда У т ^g c при m^m о . Пусть цепочка шаров C s = C ( y_s ^,ay _s || y s ||) , s =1 ,.,m, соединяющие точки y и y m 0 и присоединим к ней шар C . Пусть k о ^m - это наименьшее s такое, что замыкания шар C и ^C s пересекаются. Тогда цепочка шаров C,C i ,.,C_k 0 соединяет точки x и у . Таким образом, y g H и H является замкнутым в G i и поэтому H = G i . Лемма доказана.

Далее обозначим

E n,k = { x ^G E n : ^ax ^ k }■

Легко видеть, что множество E n k -^ замкнутое и что

E n = k =1 L ^E^.

Таким образом, ^Eη является множеством типа ^Fσ (счётным объединением замкнутых множеств) и, тем более, борелевским множеством.

В следующей лемме приводится оценка исключительного множества для меры.

Теорема 3. Пусть p (r )-буточнённый порядок, p -Lположительная мера из класса M, (p (r)) и пусть Gn-L множество построено указанным выше. Тогда существуют система шаровCs'■= C(xs,asIxs|), где xsg Gn, as= axs, покрывающая множество Gn и величина M такая, что для любых r> 1 и п > Овыполняется неравенство

X ( ^as | ^xs | ) n ¹ < Mnr n ¹ .

II x^ I < ^r

Доказательство. Пусть Gi -^ связная компонента множества Gn, и пусть x,yе Gi. По лемме 5.1 существует цепочка шаров Cs=C(xs,as||xs|), s =1,2,...,m, соединяющая точки x и y. Пусть xe C1 ,ye Cm. Если существует s 1 e {1,2,.,m} такое, что Cs 1 ^C (x, 2II x |)=# , то вводим новую У е Gi^S (х, 21|x|) nCm 1, где m 1 = min{1 ,...,m}такое, чтоCm 1nS(x,2IIxII)^# . Тогда m1

IIx - УII < 2 X as II xs| s=1

Из сказанного выше для любого s =^1,2 ,.,m 1 имеем следующие соотношения

IxJI

2II^x 11+ ^{2 a}s| ^xs| < 2II ^xll •

Аналогично

Ixs| > | x II-2| x II-as |xs|, |xs| > 2(11-) II x| > 3|x||.

(1-as )|xj| > 61 x |.

Поэтому m1

Ix - У | < 6 R X as< 6 Rn^n-1X^^^

s =1

<⁶M1 Rnn^-1(Ш) n-■ X ^

где R =||^x|,p

Из (2.3) следует, что

M1 -4 R>1

• ¹   3 R 3 RV (t)

Так как система шаров C(xs,as|xs|) образует цепочку, то каждая точка пространства покрывается не более чем двумя шарами вида B (xs,as | xs|). Учитывая это, находим, что

„ „          лp([6RIR] ^XS-Л^n-1

< 12 m₁ M 1 M 2 Rnn^-1

II x - y II < 12 m 1M1 Rnn^-1Л---VR-----'-

M₂

(^ ([ 6 RIR ]

⁶R> 1R---

\         V (R)

Из условия p e M, (p (r)) следует, что равенство IIx-yII=2IIxII невозможно.

M2<-. Если ⁿ<( 24m 1M1 m2)"^-1=ⁿ 1, то

Тогда из полученного неравенства

следует, что при n< n 1 каждая компонента множества Gn ограничена.

Теперь применяем теорему Безиковича:

“Пусть A -6 ограниченное множество в Rⁿ и пусть для каждого x e A задан замкнутый шар B (x,r (x)) ,r (x )> 0. Тогда из указанной системы шаров можно выделить последова-тельность шаров, покрывающих A и имеющих кратность не выше ^θn.”

Заметим, что число θn зависит только от Rn. Тогда существует система шаров C(xs,asrs),rs=||xs| такая, что Gnf U C(xs,asrs),rs=||xs||. Далее пишем s = 1

I \ n -1^ э ?-1 V ^{p (}C^(xs,as^rs))

.

B(R)= L (asrs) <(2r) n L — r

Заметим, что r[ 1-a)r>—r. s        s ss          s          s sss

Поэтому

B^(R)<^M3^{(2 r})n¹nTri L P (C(^xs^,as^rs))

V (r) rseM r] V”

где

μ

nM 3 (2 r)^n-1n-

([bdHnj

V^(r)

nM 3 m₄n (2 r)^n-1,

r≥1

M з-⁶1      —Ц ,M₄-⁶r> 1

^{3 1}r 2 r— (t)   ⁴

^P ([ 3 r ’^{6 r} ] ^XSn-1)

V^(r)

.

Из полученной оценки следует, что

E (^asrs) n 1 < E (^asrs) n 1 + ^Sn²" ¹M 3 M 4 nrn ¹(5.3 )

Г e| r ,2 r ]                      r_s e|0 ,r ]

Пусть теперь

Y = r > 0 41 E (asrs)П-1 • r      rsё 10 ,r]

Тогда неравенство (5.3) даёт

Y< 2 Y + 2 n-2 OnM з M 4 n,Y< 2 n-1 Wз M 4 П^

Отсюда получаем утверждение леммы при η ^≤η1. В общем случае в качестве M можно взять max (^n^{2n 1}Mз M4 ’П ) • Теорема доказана.