Оценки энтропийных чисел диагональных операторов
Автор: Ломакина Е.Н.
Журнал: Вестник Хабаровской государственной академии экономики и права @vestnik-ael
Рубрика: Теоретические и прикладные вопросы математики
Статья в выпуске: 1, 2019 года.
Бесплатный доступ
В работе получены оценки энтропийных чисел диагонального оператора
Диагональный оператор, энтропийные числа, пространства лоренца
Короткий адрес: https://sciup.org/143168826
IDR: 143168826 | УДК: 517.98
Текст научной статьи Оценки энтропийных чисел диагональных операторов
Обозначим £ "< V - пространство
всех линейных, ограниченных операторов действующих из банахова пространства Х в банахово пространство Y, где Z ■■". .' < 1 и неравенство треугольника имеет ш А' 1 А а А |л- :; } |а |а для всех .. у = /. Важной характеристикой компактности оператора Г У У /.' V яв-
ляются его энтропийные числа. Для а = г." а - энтропийное число у " опе
ратора ■ - ^ "< '.' определяется как точ ная нижняя грань множества всех чисел , для которых существуют элементы у: у: . -у-.-. = / такие, что образ за мкнутого единичного шара 3-, где Sy - замкнутый единичный шар в
. Энтропийные числа для операторов в банаховых пространствах обладают следующими свойствами [1], [2]:
для S, 7 £^ ?: V и S = ^ V S'
(I)
С.) уу?ГЬе„у5у, уу 5 W;
(iii)
В данной статье получены оценки энтропийных чисел диагональных операторов: в случае 0 Пусть . Множество всех последовательностей , , для которых конечна квазинорма образует квазибанахово пространство, в случае же , – банахово пространство. Пусть – ограниченная последовательность, положим, В случае получаем, что . Ясно, что . Последовательность KM) называют невозрастающей перестановкой . Пусть , . Пространство Лоренца состоит из всех последовательностей , имеющих конечную квазинорму При получаем. Для пространств Лоренца справедливы следующие вложения [Leoni]: 1) , если ,и 2) , если, Лемма 1. [Пич] Пусть - . -- .■■ - мерное вещественное банахово пространство. Тогда . (1) Лемма 2. Пусть 2- < У: с -, 3 < i ^ -, -. — " - мерное вещественное банахово пространство и тождественный оператор ". -.—-.. Тогда , U, где положительная константа < зависит только от ." и 5 : ДОКАЗАТЕЛЬСТВО. Предположим, что Используя оценку леммы 1, получаем Итак, что приводит к оценке Пусть , тогда и . Лемма 3. Пусть ':< /: < -, S < J < v. Тогда , где С - положительная константа из леммы 2. ДОКАЗАТЕЛЬСТВО. В силу леммы 2 для действующего в -мерном банаховом пространстве оператора имеем Зададим операторы вложения и положим . X X ft Д И р Q ее Ге Ге По свойству энтропийных чисел Применяем неравенство Гельдера с показателями , и лемму 2, получаем 11к(/„:^ -^ )}||^ ^ 11(е^ -^)}|^ ^ Сл^ Далее рассмотрим диагональный оператор который порождается последовательностью , , DkJ = {х^}, bj e 1^ (2) Не ограничивая общности, можно считать, что kt I > k2l > — > о Определим канонические операторы/n6B(^ip), Q„ e ъд^), согласно формулам и положим Wn = QnDJn. Очевидно, что 11У„11 = 11<2„11 = 1. Теорема 1. Пусть О < у < oc и 1 = f Z +7: . Тогда для оператора (2) выполняется оценка ||{an}||^< dsup,^ sen(D). (3) В частности, при у = 1 неравенство (3) имеет вид llk„}||^^ 6sup„n4e„(D). (4) ДОКАЗАТЕЛЬСТВО. Зададим оператор тождественного вложения ^n : ^oo ~* ^T и представим его в виде композиции следующих отображений: где ^n" —* ^p определяется формулой W„{xJ’L1 = «Ча?:,. Поскольку kJ > k2l 5 - kJ > °, то выполнена оценка l|WJ| < kJ-1. Известно (см. [1] 12.2.1), что e«a.:^-»^)21n. (5) Из неравенства Йенсена (поскольку q < 1) следует, чтоk^4hi, а также прямое вычисление влечётk=^^ Используя неравенство (5) и мультипликативность энтропийных чисел, имеем к < en(Z„ X -* < ) = enQn QnDJ^I, ) ^e„(/71QnD/„:^^<)-|| WJ„:^^^|| S ||/n:^ -<||- II Следовательно, Далее, умножая полученное неравенство на n1^" , получаем Отсюда sup nr k„ I < 6 sup„ n 4 en(D), n что в результате даёт требуемую оценку ||{an}||^< 6supnnr ^e„(D).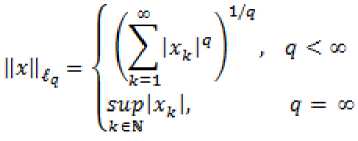
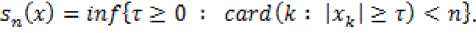
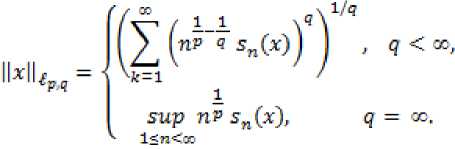
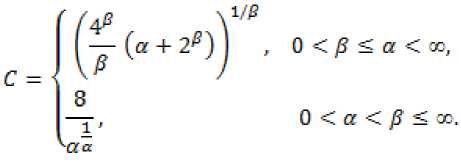
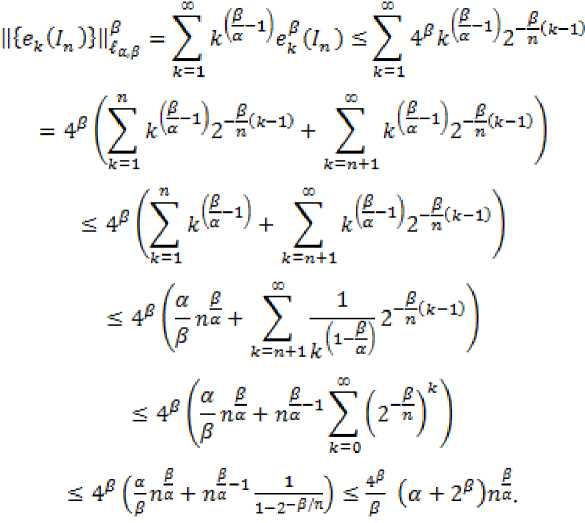
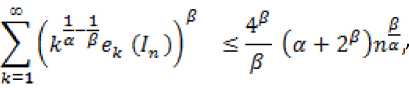
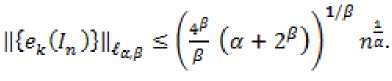
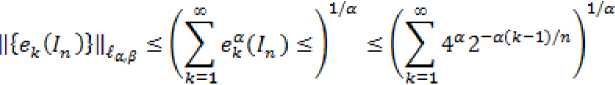
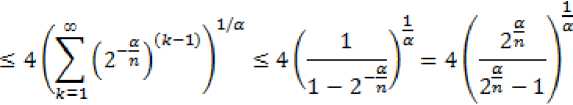
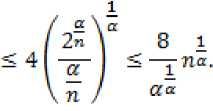
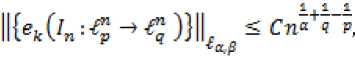
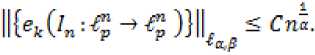
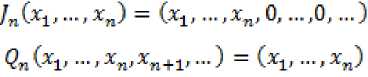
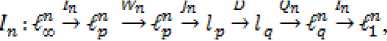
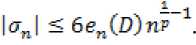
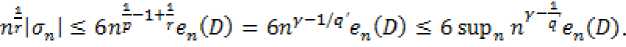
Список литературы Оценки энтропийных чисел диагональных операторов
- Пич А. Операторные идеалы / А. Пич. М.: Мир, 1982.
- Edmunds D. E., Triebel H. Function spaces, entropy number, differential operators. Cambridge Tracts in Mathematics, vol. 120, Cambridge University Press, Cambridge, 1996.
- B. Carl. Entropy numbers of diagonal operators with an application to eigenvalue problems.
- Approx J. Theory 32 (1981), no. 2, 135-150.


