Оценки погрешности линеаризации в критических случаях

Заметим, что в данном случае абсцисса точки касания окружности Аполлония для начальных положений Z i = ( х р ; у р ), z 2 = (0; с )

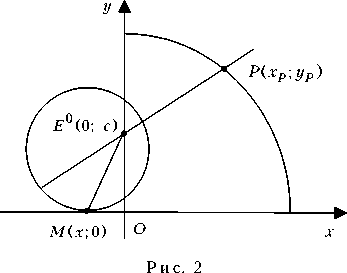
х = -

Х ²

1 -

Х ²

Х р .

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

• 1.    Петросян Л. А. Геометрия простого преследования / Л. А. Петросян, Г. В. Томский. — Новосибирск : Наука, 1983. — 144 с.

Поступила 10.03.2012.

УДК 517.977.8:53.088

ОЦЕНКИ ПОГРЕШНОСТИ ЛИНЕАРИЗАЦИИ В КРИТИЧЕСКИХ СЛУЧАЯХ*

О. В. Дружинина, В. Н. Щенников, Е. В. Щенникова

Объектом исследования является многосвязная нелинейная система дифференциальных уравнений, для которой построены верхние оценки на решения и найдена оценка погрешности ее линеаризации. Следует отметить, что система первого приближения является также нелинейной. Рассматриваемая система является более общей по сравнению с системами, описывающими критические случаи к нулевых и 2h чисто мнимых корней.

Рассмотрим нелинейную многосвязную систему дифференциальных уравнений

^у = У^ц ) ( x _s ) + А^ ( t , х _р ..., x _q ) +

⁺ £ _Х ( ц+^{а )} ^, ^ _, ) + д ^ { _t ) _

7 = 1

= M_s ( t, х ) + Д ₅ ( t )

с начальными условиями

( ^Xi ( t ₀ ) , ... ,^ ( t ₀ ) ) ^Г = X ( t ₀ ) = ^ ( < о ) - ( < о ) = х ₀. Здесь Х^ ( x , ) : Rⁿ= ^ Rⁿ= и Х^ ( t , x_i, ..., ..., x _q ) : R ⁺ х R ” х ... х R ” ’ ^ R ” , ( s = i q ) , x _s e R ” , Rⁿ ' ® ... Ф R ” ’ = R ” , R ⁺ = { t : t >  г

> to > 0}, x = (хГ , ..., Xq I , векторные функции Х^ (X, ) и Х^ (t, Xi, ..., Xq ) являются непрерывными по совокупности переменных, кроме того, непрерывно дифференцируемыми по переменным x^ ..., Xq. Векторные функции Х^У^ (t,Xi, ...,Xq) : R+х R” х ... х R” ^ R” (s, j = 1,q), Х,") (x, ) определяют связи в подсистемах, а Х^ (t,Xi, ...,Xq) описывают взаимосвязи подсистем, т. е.

X _s = x S * ) ( x _s ) + Х^ ^ t , X i , ..., X q ) , s = i, q , векторные функции   X *⁺“ ^ t, X i , ..., X q j :

: R⁺ х Rⁿ обладают теми же свойствами, что и Х^ * ^ ( t , X i , ..., X q ) , Д , ( t ) — непрерывные ограниченные векторные функции,

IIДs (t)|| < ДS, Д3 > 0, M, (t, 0) ^ 0, s = 1,q. Верхний индекс т означает транспонирование, а индекс * = — > i, р и q — нечетные, q указывает на порядок однородности Х," (x,) и х[*) (t,Xu, ..., Xiq), для векторных функций Х^.*""1 (t,xi, ..., xq) верхний индекс р + а, 0 < а = const также указывает на однородность относительно x^ ..., Xq. Всюду в дальнейшем будем считать, что норма вектора является евклидовой.

В качестве системы первого приближения по отношению к системе (1) примем систему

= ^р)(Уз) + М’' (t.У1- --Уд) + Д3(t)- (2) at для которой (xf (t0), ..., xq (t0)) = x(t0) = = У (to) = (у! (to), ..., yq (t)) , S = 1, q. Посу-ществу, система (2) является линеаризованным вариантом системы (1).

Будем предполагать, что справедливы неравенства

||^Х 1 ^ ’ ( ^ У 1..... y q )|| <  2 ^ 1 ,- 1-У/1 " -    ⁽³⁾

IХ^ф.И   У , )|| <  1 6„|^Г” «> при ||x-|| < Г у , ^ 2 у = ₁ ^rj = ^г . Здесь а^ и b_{s j} — некоторые положительные вещественные числа и, кроме того, а^ у достаточно малы [3], s, j = 1, q.

Предположим, что нулевое решение систем

^ = xs") (ys), s = l,q. (5) at асимптотически устойчиво. Тогда согласно теореме об асимптотической устойчивости Зубова — Красовского [2, гл. 1; 3; 4] для каждой системы (5) существует функция Ляпунова, удовлетворяющая условиям:

Ir + i -*

C i s ^s|r^{i -}* <  V s ( y s ) <  C 2 s Ы

”"* ,

||grad^ (У2 )|| < c3s|lysK dVs dt

< - C4s ^sl Г

^пр^и  bsll <  ^rs ^,

= ' ,

s = i, q . Здесь

/у q

\ ² 3 = 1 ' s

г — достаточно большое четное веществен ное положительное число; c,s, C2s, C3s, C4s — постоянные положительные вещественные числа, , = l, q.

С целью получения искомых оценок найдем вначале верхние оценки на решения системы (1). Для этого зададим функцию Ляпунова для системы (1) в виде

q

V ( х ) = ^ d _s V _s ( х , ) ,          (7)

, = 1

где a_s > 0 — вещественные числа. Здесь V _s ( x _s) удовлетворяет условиям (6).

Найдем далее dV Ч   d^ (xs)

=   d„< dt (1) 1 s dt

s ( - c₄ s|| x s|Г + ( grad V s ( X s ) , i= i

( x ( s * ⁾ ( t, X i , ..., X q ) + f: x Sy “ ⁾ X ^x                              j = i

X ( t, X i , ..., X q ) + Д s ( t ) )).

Очевидно, что q

= 2 d_sV_{s 0} .

s = 1

q

V (^о) = Vo = 2 dsVs (д0) = s=1

Исходя из определения функции У(д) в виде (10), всегда можно найти положительные вещественные числа « 1 , « 2 , « 3 и « 4 такие, что будут выполняться неравенства:

С учетом оценок (3), (4), (6) и ограничений на A_s(t) неравенство (8) преобразуется в неравенство

«з ^ Г ^{+ 1 -ц} <  « 2 Iksl г ^{+ 1 -ц} ^ s= 1

dV dt

q

< 2 ds i=1

( -c _{4 s} + ^c ₃ s^й 1 ss ⁾ ksll +

I

( q

2 ^й 1 s ₎ ||^дill ^{+ c} 3s|ks||   ^Ц X ⁽9⁾

^ 2 d s C 1s\ kslГ ^{+ 1 -Ц} ^ V ( д ) <  s = 1

< 2 d s C 2s\ ksl Г ^{+ 1 -Ц} <  « 2 2 Iksl Г ^{+ 1 -Ц} <  s = 1                            s = 1

q

^{2 Ь}Ц ||^д/||

| ^Ц+“ + A s

< й ₄ kl Г ^{+ 1 -ц} ,

■

Введем в рассмотрение матрицы W ^ = |®SP| , где ®k = - c _4s + c _3s a _1sj при s =/, апри s * / ^ SP = ^c 3 s^si ^и W ₂ = д | ^2: ^ , ^гд^е ® Sp =

= C 3 _Sb i_ _S j . Матрица W_t является матрицей Метцлера [1, с. 199 — 207]. Будем считать, что величины а^ такие, что разности -C 4 _s + C 3 _stt i _s j будут отрицательными при s = = i, т. е. - c _{4 s} + c _{3 s}a _{1 ss} <  0 и, кроме того, существуют такие значения постоянных d_s ( s = 1, q j , для которых справедливы неравенства:

• У^ ¹ ^ = ^d i ( ^-cn ^{+ c} 3i « iii ) ^{+ d} 2 ^c 31 ^a 121 ⁺ ••• ⁺

^{+ d} q ^c 31 ^a 1 q 1 <  0^, к² = ^d1^c32^a112 ⁺

+ d2^-c42 + с31й122) + ■■■ + dqc31a1q2 < 0, у^ = d1c3qti11q1 + d3c3qaY2q + ...  +

^{+ d}q ^ ^{- c} 4 q ^{+ c}3q^a1qq ) <  °.

Далее введем обозначение

q

«У = 2 ^ds^c з s^ъsj ^, j = ^1, q .

s = 1

Очевидно, что справедливы неравенства:

- у = max | у ^{( 1 )} , ■■■, y ^(q^ <  0, у = max ]у^{( 1 )} , ■■■,у ^{(1 )}1 >  0.

1             q

где

Q 1 = mln { d_sc 1 _s } , ^ 2 = min { d_sc 2 _s } .

1 1

Введем преобразование p = V ¹ ^ ™ ^{+ 1 ц}\ Тогда исходя из преобразования и условий (11) будем иметь:

||д|| >—^Г —, ||д|| <  ... ^Р. . . (12)

1/ ( m + 1 -ц )              у ( m + 1 -ц )

^й 4'                  ^й 3

Перепишем далее неравенство (9) с учетом неравенств (10) и (11). В результате получим неравенство dV dt (1)

г        Г +а

< - й₅У д + ЙУ 1 д +

+ c₃ A ИГ ^-Ц ,

где «₅, « 6 и С 3 — положительные веществен-

7 т ные числа, A = 2 A _s.

s = 1

С учетом введенного преобразования и неравенства (12) в неравенстве (13) перейдем к одной неизвестной функции р = р ( t ) , т. е.

dP< —---,  О"5 , , р^ + dt т + 1 - ц ^ й(™+“)/(™+1-^)

° 1^Й6^С3      _рц+а ₊       ^С3 ^А

( т +а )/( т + 1 -ц ) ^Р          „( т -ц )/( т + 1 -ц ) ’

Йз                      Йз             / дифференциальное уравнение сравнения для которого имеет вид:

du dt

т + 1 - ц

_-      од₅

( ^m +a )/( ^m + ^{1 -}^ )

V “ 4

um

+

O i ti g C g

( т +а )/( т + 1 -ц ) 3

и ^ц+а

ry¹'" \

( ^{т -}ц )/( ^{т + 1 -}ц )

“ 3             J

Ф ( u ) .

U ^ ⁰ ( у , У ) , Д 3 , д ₄, д ₃, д ₆, с ₃

при а ^ ^{т +1 0} ||^₀1| <  м ^ ⁰ ( у,у_ь а₃, а ₄ , а₅,а₆, с₃ ) .

Перейдем к построению искомой оценки погрешности линеаризации системы (1). Для этого введем в рассмотрение систему

Здесь р о = р ( ^ о ) = V ^{1 ( т + 1 0 )} ( д ( ^ о ) , .... X q ( < о ) ) = V ¹ ( ^{т + 1}^ ( t o ) <  а ^ ^т+1—0 \|< При^мем Р о = Р ( ^t o ) = ^м о = ^м ( ^t o ) = ^а \ ^{т + 1 -ц} ко|| . Постоянная d₄ определяется из уравнения V ¹ ( ^{т + 1} о ) ( t o ) = а ^{1 т 1 1} ° |до|| - Тогда по теореме сравнения [1, гл. 5; 5, гл. 1] имеем:

р ( t ) <  м ( t ) при t >  t o.

Пусть алгебраическое уравнение

Ф ( м ) = 0

в области м > 0 имеет решение. В данном случае их будет не более двух, т. е. м10 (у, У1, аз, ai, а5, а6, С3), м^0 (у, У1, аз, а4, а5, ад, С3).В дальнейшем будем их обозначать через м^ц (•) и и^0 (•). Пусть 0 < м^0 (■) < < ^0 (■).

Очевидно, что

^ — Х , ^{ц )} ( d s ( t ) + s , ) - Х ( ^{ц )} ( d , ( t ) ) ^{+ Х ц )} ( ^t , У 1 ( ^t ) + S t , ..., d q ( ^t ) + e_q ) ^-

+

- Х , ^{ц )} ( t, d 1 ( t ) , ..., d q ( t ) ) +           ⁽¹⁵⁾

₊ f _Х (Д^{+а )} ( t, д ( t ) , ..., _Xq ( t ) ) S — 1^ .

j— 1

Здесь s _s ( t ) = x_s ( t ) - d_s ( t ) , s = 1, q. Так как Д ( ^t o ) = d s ( ^t o ) ^{, то} S s ( ^t o ) = ° s = 1Tq.

Систему (15) можно записать в виде:

^ ^{= (}Л ( ^e s ^, У , ( ^t )) ⁺ Ф 1, ( ^{t ,} У 1 ( ^t ) ^, ■■■^{, y}q ^ ⁾ , ^е 1 ’ ■"’ ^e q ) ⁺             Об⁾

+ £ ^^ (^ ^1 ^t ^ , ■■■. х^ ^у i=1

где ф ₅ ( s s . y_s ( ^t ) ) = Х <^ц > (y_s ( ^t ) + S s ) - % (^ц > (y_s ( ^t ) ) .

V 1 s ( t , ^y i ( ^t ) , ■■■, ^y _q ( ^t ) , ^e 1 , ■■■, £ _q ) —

Ф (u )

> 0 при ( 0 <  u <  u ^^ц ( • ) ) Л ( u >  u ^ ^ц ( • ) ) , = <

= Х^) ( ^t , d l ( ^t ) ⁺ S i , .... ^yq ( ^t ) ⁺ S q ) ^—

< 0 при u ^ ^ц ( • ) <  u <  u ^^ц ( • ) .

Отсюда следует, что м ^{1 0} ( • ) является асимптотически устойчивым положением равновесия уравнения (17), а м ^ ⁰ ( ■ ) — неустойчивым. Значит, решение м ( t,t o , м о ) уравнения (17) монотонно стремится к м ^ ⁰ ( • ) при м о <  м ^ 0 ( ■ ) и t — t o —^ +w .

Так как р ( t ) <  м ( t ) при t >  ( о >  о, причем р о = р ( t o ) = м ( t o ) = м о , то с учетом неравенств (13) и (11) следует верхняя оценка на решения системы (1), т. е.

sup ||д ^{( t} , ^t o , Д о )|| <  _{а 3 (т} ¹ _+1—0) max [ д ^/ ^{( т + 1 —0 )} | |^ о|| ,

^{— Х} 1 ^{Ц )} ( ^t > d i ( ^t ) , ■■■> d q ( ^t ) ) > S = 1, q.

Предположим, что для каждой системы

^ ^ Т ^— Ф ^ ( ^е^ У 8 ( ^t ) ) ^{, s — i,} q       (17)

at

существует функция Ляпунова V ^ s ( t, S s ) , удовлетворяющая условиям:

1) Д 1₅ Т (I |S s| I) < V 1s ( t , 5 s ) < Д _{2 5} ^ (I |5 s| I) ;

5 V_t s ( t, S s ) SS s

< M 1 s ;

dV 1 _s ( t , 5 s ) dt

( ¹? )

< ^- C 1s^ (||Es|I)

при

||e _s|| <  2 r_s , s — 1, q ,

где о^ , a ^ _s , c _{l s} и M _s — положительные вещественные числа, функция ¥ (||-||) — неограниченно строго возрастающая, V ( 0 ) = 0. Будем считать, что при y_s е R"^s , &_s е R"^s и t >  t o >  0 справедливы неравенства:

< £ р ^dt ( 16 ) j- 1

dV

" C is * (Il^Ss I) ⁺

⁴⁾ ||_Фк ( t, s_b ..., 6 q , у _х ( t ) , ..., y_q ( t ) ) <

q

+ M1s 2 Bs, * (| s 7| I) i-1

+

q

< 2 вчч (е A I)

i - 1

⁺ 2 ^dS ^{1, ) M} 1 s 2 ^bsi Ik i ^ )|P ^{, s - 1} q. ^{i -1            i -1}

⁵) 2J^r^{a )} ( t, ^ i ( t ) ,..., ^xs ( t ) )| <

Далее применим тот же прием, что и при построении верхней оценки на решения системы (1), т. е. введем в рассмотрение матрицу

м - ii^mis/i r ’ q , в которой 1,1

• <    2 b, |kу ( t ) P, i = i

где B_q и b^ — положительные вещественные числа при |kj| <  T j , ||sj| <  2t_s. Тогда с учетом неравенств 4 и 5 и того, что для каждой системы (17) существует функция Ляпунова, удовлетворяющаяусловиям (18), будем иметь:

dV dt

< ^{- C} 1 s * (I |^S slI) ⁺ ( grad V i s ( ^{t , S} s ) ^, ( 16 )

• ^Y 1 s ( ^t . У 1 ( ^t ) , -. ^ q ( ^t ) , ^S 1 , -. ^S q ) ) ⁺

+ 2 p^{+a )} ( t, Д 1 ( t ) , ..., X_q ( t ) ) <           ⁽¹⁹⁾

i - 1

• <    -T s * (IЫI) + M . 2 B^V (| |s iI) +

i - 1

• ^{+    M} 1 s 2^ Iki ( t )| p, s = 1, q.

i - 1

Для системы (16) выберем функцию Ляпунова в виде:

v ₁ ( t, е ) - 2 Pv_s ( t, s_s ) , (20) i - 1

где d s ¹ ) >  0, s = 1, q. Учитывая неравенства (18), условия 4и5, а также задание функции Ляпунова V 1 ( t, s ) в виде (20), из неравенств (19) получим:

• _-    J" ^c 1 s ⁺ M i s B sj при s ^- i , ^{m i si} [ M i _s ^Bsy ^пР^{и s} * j .

Матрица M есть матрица Метцлера [1, с. 199 — 207]. Пусть -c1s + M1sBSjM < 0 при s = i и существуют такие ds (s - 1, q), при которых выполняются неравенства:

^у2 ^ ^{- d}V ( " ^у11 ⁺ ^ 11 ^ 11 ) ^{+ d}: i ^ ^" 12^S21 ⁺ ... ⁺

+ d <^ M 1 _qB 1 _q <  0’

• ^у^ - ^dP^M 11 ^B 1 q + ... + ^dq_ 1 ^M q- 1, q ⁺ ... ⁺

• + d^ ( -C i _q + M i _q B _qq ) <  0.

Тогда - у ₂ - шах | « 2 ¹ ^ , ..., Р| <  0. Выберем положительные вещественные числа д ⁽¹⁾, ^й 2 ^1> , "Р ^{1 й} 4 ¹ * такими, чтобы выполнялись нервенства:

• ^йР (I s о < ^й( ^{1 }} 22 Р* (Iksl D < S - 1

• <2l ^d^ й i s * (| ^slI) <  V 1 ( t , s ) <  s - 1                                     (21₁)

< 2 dP s* (I ksl D < P 2 d s ¹⁾ * (I ksl D <  s - 1                             s - 1

• < P* (IHI).

Тогда неравенство (21) примет вид:

dV dt

< - V ( t, s ) + £ d

( 16 )        « 2 ⁾                ( = 1

Исходя из определения функции Ляпунова в виде (23) и с учетом неравенств (2ф) и (24 j ), получим искомую оценку, т. е.

g

^M 1 s Е b_sj Цху ^{( t )}|| ( = 1

I ц+а

sup I^{s ( t )}|| <  t > t o

« 2 ^{) д} 6 ° 3 _т - 1

° 2

/Г

V (™ + 1щ) «О k L 3

X

Дифференциальному неравенству (22) соответствует дифференциальное уравнение сравнения

Ц = - 42г Р + Е ^К Е b s ₃ Ь ( t )|Ц ^+а (23) ^at      « 2 ⁾      ( = 1           ( = 1

с начальным условием

Р ( t o ) = Р ( t ) = V 1 (ф , в о ) =

= q Е ^ S^{1 ) v}s ( t o , s o ) = ^V 1o -

S = 1

Отметим при этом, что s ( t o ) = 0. Значит, V 10 = 0.

Применяя снова теорему сравнения, получим:

V ( t , е ( t ) ) <р ( t ) при t >  t o >  0.

Интегрируя уравнения (23), находим:

р ( t ) <      Е dl¹);^ |х _} ( t )|Р,

⁰ 2 s , j= 1

из которого следует неравенство:

л ( 1 ) q

Ч (t,е (t)) <     Е d^Msbsj |kj (t)|Г о2 s,j '

(24) при t >  t o .

Введем в рассмотрение величины г3^ = = d^Msbsj. Пусть о = max

1 < j , s

У ^{( s} ’ ^{j )} ° 3

> 0.

Тогда неравенство (24) получит вид:

V 1 ( t , e ( t ) ) <  Е |k j ( t ) Г . (24 1 )

⁰ 2 s , j = 1

X max ^У(m+1 г) ||х0||, ^УГх пц+а

X (у, Ур Яз> ^4, ^5, ^6’ с3 )|

)

Таким образом, доказана теорема.

Теорема. Пусть:

• а)    x_S = 0 — положения равновесий системы 5 с _s = M_s ( t , х ) ’ ( s = l, q );

• б)    выполнены все ограничения на правые части системы (1);

• в)    для систем (5) и (17) существуют функции Ляпунова V_S ( t , s ) и V 1 _S ( t, s _S ) , удовлетворяющие соответственно условиям (6) и (18) ( s = l? q );

• г)    алгебраическое уравнение Ф ( м ) = 0 в области и >  0 имеет решения 0 <  « У ⁴ ( у, У 1 , й ₃, а₄’ а₅, й ₆, с₃ ) <  и^ ( у,У у , а₃, а₄, а₅, а₆, с₃ ) ;

• д)    а ^ ⁴ ||^o|| <  ^иТ ( У’ У 1 ’ « 3 , « 4 , « 5 , « 6 , С 3 ) .

Тогда:

• 1)    решения системы (1) существуют для всех t >  t o >  o;

• 2)    справедливы оценки (14 ^ ) и (24 2 ).

Замечание. Исходная система (1) является более общей по сравнению с системами дифференциальных уравнений в критических случаях. Однако если одна из векторных функций ^к' ' окажется линейной, то такая система будет описывать критический случай q_s нулевых корней [2; 6]. Также можно рассматривать другие критические случаи. Метод получения верхних оценок в критических случаях и оценок погрешностей линеаризации совпадает с разработанным в данной работе методом построения указанных оценок.