Один из механизмов возникновения высокочастотных колебаний при точении

Известно, что резание сопровождается широким спектром колебаний [1 – 9]. Они проявляются, в частности, в волнах напряжений, распространяющихся от зоны резания в упругую среду металла, которая представляет систему с границами раздела сред. Колебательные процессы оказывают существенное влияние на качество обработанной поверхности и энергоемкость обработки резанием. Априорная оценка частотных диапазонов возможных автоколебаний открывает перспективы для определения границ допустимых режимов обработки, переход через которые сопровождается ухудшением качества обрабатываемых поверхностей, а в некоторых случаях и разрушением технологической оснастки.

ВОЛНОВЫЕ ПРОЦЕССЫ В ЗОНЕ РЕЗАНИЯ

Поверхность сдвигов является границей раз- дела двух сред: упругого тела, подвергнутого воздействию сил резания, и упруго-пластической среды образуемой при этом стружки (рис. 1).

Упругое колебание поверхности F , как гра- ницы раздела двух сред не стеснено, так как выше ее происходят пластические деформации с потерей напряжения. Частота колебаний поверхности сдвигов, вызывающей волны напряжения, уходящие в тело B , и будет искомой высокой частотой возмущений.

Предположим, что волны, уходящие вглубь тела B от поверхности F , продольные и пло- ские. Уравнение, описывающее распростране- ние волны [10], имеет вид

( У ^

x = a cos to t-- l и n )

где a - амплитуда; to - круговая частота; иn - скорость распространения волны, определяемая из соотношения [8]:

^u n

E

N P

,

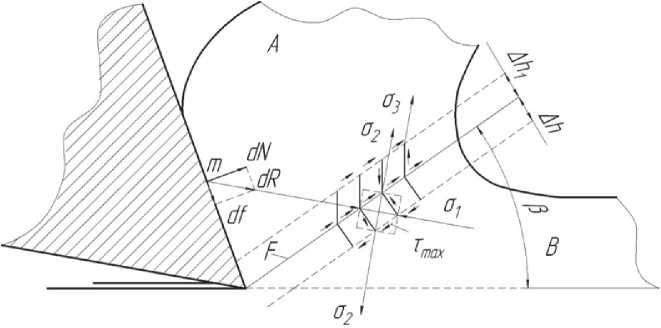
Рис. 1. Колебания величины упругого напряжения поверхности сдвигов

где E - модуль упругости, р - плотность. Для стали её величина находится в пределах 5000÷5800 м/сек [5 – 8].

При прохождении каждой из образующихся волн напряжения через слой A h наибольшее значение относительной деформации £ слоя будет, как известно [8], тогда, когда слой находится в положении равновесия. В этот момент слой наиболее деформирован и возмущающий импульс со стороны поверхности F равен нулю.

Пусть (рис. 2) x – первоначальное расстояние между двумя точками, лежащими на верхней и нижней границах слоя Ah, a x + xd - то же расстояние в конце колебания слоя по направлению нормали к поверхности F и yd – величина колебания. Тогда при относительной деформа-dx ции — = г среда оказывается сжатой, если dy

взять производную по переменной t от уравнения (1):

i = x'

dx dt

г- a to sin to t -

I

u n )

Кроме того, взяв производную по направлению нормали к поверхности F , то есть по yd ,

получим dx

£ = dy

a ro .

---Sin ro t -

u n v

y ^u n )

Складывая уравнения (2) и (3) найдём

dx dx                          i

— = -u — или i = u„£, а также г = —. (3а)

dt dy          ⁿ              u _n

dx             dx

— <  0 . Если же — >  0 , то среда оказывается

dy            dy

растянутой.

Скорость колебания точек i среды слоя будет, очевидно, наибольшей в положении равновесия, чему, как сказано выше, соответствует наибольшая деформация слоя A h .

Зависимость, связывающую скорость волны, скорость колеблющихся точек слоя и относительную деформацию £ можно найти, если

Чтобы найти искомую высокую частоту колебаний площадки F и сопредельного с ней слоя A h , наиболее удобным будет воспользоваться понятием потока энергии. Определим поток энергии, проходящий в тело детали B нормально площадке F .

Введем следующие обозначения: U – кинетическая энергия, V – потенциальная энергия и A – полная энергия проходящей волны. Объем тонкого слоя A h обозначим через q и будем рассматривать его как объём участка среды, имеющего массу m .При этом следует отметить,

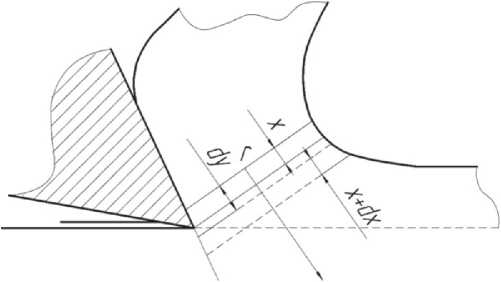
Рис. 2. Колебание точек среды поверхности сдвигов при прохождении волн напряжения

что при волновых колебаниях, в отличие от колебаний точки, принадлежащей системе инструмент – деталь, потенциальная энергия колеблющегося участка среды V и кинетическая энергия U изменяются в одной фазе, то есть возрастают или убывают одновременно. Объясняется это тем, что энергия волны передается от одного объема участка среды к другому. Следовательно, полная энергия волны напряжения, проходящей через слой A h , как участка среды, имеет переменную величину, а поэтому напряжения на площадке сдвигов и в сопредельном с нею слое A h также переменны. Это периодическое изменение напряжений и служит источником возмущения процесса резания на высоких частотах.

Формула, выражающая величину полной энергии волны, проходящей через участок среды, как известно, имеет вид:

В формуле (7) величина a – это амплитуда волнового колебания площадки. Величина амплитуды определяется из известного соотноше-

2  2A ния ад =---(где к - коэффициент упругости

k системы).

Подставляя это значение амплитуды в формулу (7), получим

р 12 A 2 к P = ^- k рю иnF,

где A – полная энергия колебания системы.

Круговая частота го и период колебания T ,

2 п как известно, связаны зависимостью T = — го

.

y

A = U + V = q р а ² го ² sin ² ro t - — . (4)

Заменяя в выражении (8) величину го величиной T , получим

V и n 7

Здесь р - плотность тела B и q р = m представляет собой массу слоя A h , как участок среды, через который движется волна.

Ввиду того, что отношение величины полной энергии A к объему q , в котором она заключена в данный фиксированный момент времени, представляет собой плотность энергии, выражение

р  4 п ² A -

P = , р . и nF, T2 k

Aq =

A

q

2 2-2

= qра го sin го t

^^^^^^^^

y )

V U n 7

и будет определять её величину. Заметим, что плотность энергии Aq , так же как и сама энер-T гия, изменяется за время t = —, равное полупе риоду возмущающего колебания площадки F .

Из формулы (5) видно, что среднее значение квадрата синуса за полупериод равно половине, поэтому среднее значение плотности энергии

Aq = 2 Р a ГО .

чем и определится величина среднего потока энергии, направленного в среду обрабатываемого материала. С другой стороны, через площадку контакта резца и стружки F' на передней поверхности резца будет протекать энергия, A плотность которой составит , где в свою и nTFf очередь иnTF' - объём, занимаемый энергией за время T . Умножив плотность энергии на тот же объём и разделив на время T , получим средний поток энергии, проходящей через площад-A ку F ,т. е. —cos Y .

Так как средние потоки энергии, проходящей при колебании через площадки F и F' , равны и направлены нормально площадкам, то, подставив в формулу (9) среднее значение потока через площадку на передней грани резца, выраженного посредством полной энергии колебания системы, получим

За все время, равное периоду колебания площадки F или слоя A h , количество энергии A = A q и n FT (где и _nFT - объём, занятый энергией за время того же периода T ). Разделив величину энергии A' на время T , получим средний поток энергии P . Подставив из формулы (6) значение плотности энергии, получим, таким образом, величину среднего потока энергии

A    4 п ²

cos у T

4л2р п откуда T =-----—n

T ²

A

Ру^и n F , k

F — cos у .

или P = A и . qn

P = — ра 2го2и nF

Если же период T выразить через частоту в герцах v , то получим искомую величину высоких частот возмущений процесса резания (Гц)

k

v =—2-------

4 п pu _nF cos /

.

Для того, чтобы формула приобрела вид, пригодный для практического использования, необходимо следующее:

• -    коэффициент упругости системы следует

P принять из общеизвестной зависимости k = f

(где P – сила, деформирующая систему при статической нагрузке, f – деформация, отсчитываемая от положения равновесия и получившаяся под действием этой силы);

• -    выразить нормальную составляющую силы P по отношению к площадке F , через главную составляющую силы резания P_z согласно зависимости [4] P = P_z sin β (где β — угол сдвигов).

Угол сдвигов β , находится из зависимости Р = 45 + у - arctg ц [4] (где Ц - средний коэффициент трения стружки по резцу). Приняв во внимание это соотношение, формулу (10) можно переписать в виде

⁾ . (11)

• 1    P_z sin ( 45 ^° + γ - arctg µ

ν=⋅

4 ρπ ²        F υ _n f cos γ

При практических расчетах возмущающей частоты ν площадку F можно выразить через ширину среза a и подачу S в мм/об, т. е.

F =

as sin Р .

Предложенная зависимость устанавливает связь частота автоколебаний, сопровождающих процесс резания с характеристиками обрабатываемого и инструментального материалов, геометрией режущего клина и режимными параметрами.

ЗАКЛЮЧЕНИЕ

На основании проведенных исследований подтверждено, что источником автоколебаний высокой частоты, генерируемых в зоне резания, является динамика деформирования материала при его разрушении по плоскости сдвига. Эта плоскость представляет поверхность раздела двух сред, инициирующую волновые процессы распространяемы в тело заготовки и стружки. Их характер и параметры в значительной степени зависят от свойств обрабатываемого материала (модуля упругости и плотности), характеристик инструмента (материала, переднего угла и качества передней поверхности) и такими режимными параметрами, как подача на оборот и ширина среза. Отмечено, что скорость резания влияет на них опосредовано, через угол сдвига и главную составляющую силы резания..