Один случай формирования хаотических аттракторов в динамической системе резания

Введение. Динамическая система процесса резания, базовая модель которой характеризует взаимодействие про странственной динамической модели подсистемы инструмента с динамической связью, формируемой процессом об'

Машиностроение и машиноведение

работки, может служить примером, иллюстрирующим различные эффекты нелинейной динамики. В известных исследованиях в области динамики процессов обработки на металлорежущих станках главное внимание уделялось рас-

– принимался во внимание случай, когда за счет существенных изгибных деформационных смещений инструмента, вызывающих уменьшение переднего угла режущего инструмента, силы резания не уменьшаются, как в отмеченных выше работах, а возрастают. Тем самым формируется положительная обратная связь, способствующая самовозбуждению системы резания. Ниже будет показано, что в этом случае, как правило, в окрестностях равновесия образуются странные (хаотические) аттракторы. Приводимый в статье материал дополняет известные примеры образования хаотических аттракторов [19-24].

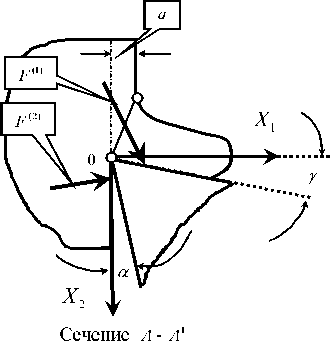
Математическая модель. Как и в ранее опубликованных работах, будем рассматривать базовую динамическую модель механической части системы в виде [11 -14], (рис. 1):

d ² X , dX

m —т- + h--ccX = F (t), dt2 dt

m

m

01 h i

1,1

, mh

—I              l_ 1 ,^

^h 2,1              ^c 1,1

, c h 2,2 J        [_c1,2

c 2,1

^c 2,2

— соответственно матрицы инерционных, диссипативных и упру

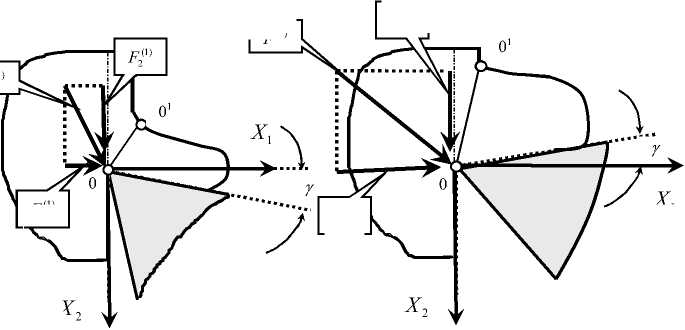
гих коэффициентов подсистемы инструмента; X = { X_ьX ₂} T — вектор упругих деформационных смещений инструмента в плоскости, нормальной к поверхности резания; F ( t ) = { F ₁( t ), F ₂( t )} T — вектор сил резания. Упругие деформа-

V ся постоянной. Она определяет постоянную составляющую скорости резания V . Поэтому в установившемся состоя-Sp const

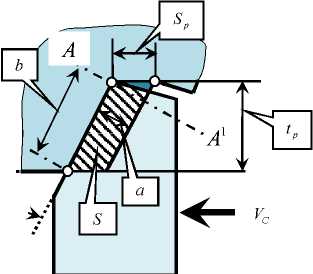
F ность F(2), то есть F = F(1) + F(2) (рис. 1). Однако в рассматриваемом случае влиянием сил, действующих на заднюю грань инструмента, можно пренебречь, то есть угол а есть величина большая, что характерно, например, для tp                                      Sp рии инструмента однозначно определяют ширину срезаемого слоя b и его толщину a, так как a = SP sin ср, а b = tp / sin ср (ср — главный угол инструмента в плане (рис. 1)). Деформационные смещения в направлении, нормаль ном к плоскости (X1 - X2)не принимаются во внимание, так как деформации в этом направлении практически не вызывают изменения площади срезаемого слоя S . Параметры m, h и c можно определить по правилам, изложенным, например, в [11].

Главной особенностью рассматриваемого случая является изменение переднего угла режущего инструмента при деформационных смещениях инструмента в направлении X 2. В результате имеет место уменьшение значений переднего угла вплоть до отрицательных его значений. Поэтому, во -первых, по мере увеличения деформационных смещений в направлении X 2 имеет место увеличение объема пластической деформации в зоне резания, и, как следствие, увеличение модуля силы резания [26]. Во -вторых, силы резания в направлении X ₂ возрастают непропорционально быстро [11]. Кроме этого, как и в ранее рассмотренных случаях [27, 28], имеет место запаздывание изменения сил по отношению к деформационным смещениям инструмента. Эти особенности процесса резания можно учесть, если рассмотреть силы резания в виде следующих зависимостей:

р ⁽¹⁾ — У⁽¹⁾1 + а(^,У⁽¹⁾')³ '

F 1   ^_ Л1 P b L a  Y1 Гт^u( Y2 ) •

F 2⁽¹⁾=X2P b [ a-Y1⁽²⁾] + P Y 2⁽²⁾ ;

T (1) ^dX 1 , v _ y(1) •

T ¹ XTX ¹ - Y ^;

T

■(2) ^dX 1 . Y - У(2) • ¹ ^T^{+ X 1} - Y •

(1) ^T 2

T ₂

dX2 + X -y(1)-^T+X2 "Y2 • dX2 + V - У(2)

^T^{+ X 2} " Y ² •

где X 1 , X ₂ — деформационные смещения вершины инструмента в двух ортогональных направлениях в [мм] ; /₁, %₂ — угловые коэффициенты, удовлетворяющие условиям нормировки (%₁)² + (%₂)² = 1; я, b — соответственно толщина и ширина срезаемого слоя, зависящие от технологических режимов и геометрии инструмента в [мм] ; ос — коэффициент, определяющий приращение силы к приращению объема деформируемого материала, имеющий смысл плотности в [кг/мм³]; р — составляющая коэффициента жесткости процесса резания в /кг/мм]; T®, T /² ) , T ₂⁽¹⁾, T У — постоянные времени, определяющие запаздывание изменения сил по отношению к деформационным смещениям (1) /т’(2)        (1) /'r(21

инструмента относительно заготовки в [cj. Причем, 11 ) Т ) и T ) ( 7 2 ⁽ ) .

f <]>

ф

р w F 2

F(,)

F/'1

Рис. 1. Ориентация осей деформационных смещений и сил, действующих на переднюю грань режущего инструмента

F ⁽¹⁾

F 1

Таким образом, математическая модель динамической системы резания представляется в виде следующей системы:

d X1       dX 1                 dX 2                          (1)        (1) 3_ m 7 + hU     +c1,1 X1 +h2,1      + c2,1 X 2_X1 Pb[a  Y1 J + a(Y2 ) ;

dt ²       ’ dt                   dt

d2 X      dX, m--— + h 9---+ c,2

dt ^{2      2,2} dt ²²

Xh 2     1,2 dt	t- c 1,2 X 1
T (1) dX 1	_y (1)-
1 dt        1	; 1
T (2) dX 1 X	(2). ;
1 dt        1	1
T (1) dX 1 , Y TX 2 dt       2	(1) - Y 2 ;
(2) dX, у T 2 ^T+ X 2	_ y (2)

,

- 1=X2p b [ а-У /²⁾] + p y <²⁾;

Машиностроение и машиноведение

которая учитывает все основные свойства динамической системы резания, отмеченные выше.

Свойства равновесия . Равновесие системы определяется исходя из условия: изменения деформационных смещений инструмента отсутствуют. Следовательно, точка равновесия ( X * , X 2 ) определяется из уравнения

⁽ c i,i + Xi Pb ) X * + c 2,1 ^X 2 = Xi P^ba + a( X 2* ⁾³ ;

⁽ c i,2 +%2P b ) X * + ⁽ c 2,2 -P) ^X 2 = X2 pba .

Анализ (4) приводит к необходимости рассмотрения следующего уравнения:

а ( X 2 )³ + С^Х*^ =0,                                  (5)

где

С 2,2 (c1,1 + Х1Р b) - [ c1,1P + Х1Р bP + (c1,2 )2 + /2 Pbc1,2 ] = A-B (ci,2     2 b)                             D обобщенная жесткость системы;

„    К 1^С1,2 Х2^С1,1

F =-----------pba — суммарное значение силы. В динамической системе резания параметры A , В , D и сум'   (Нд+Х2Р b )

марная сила F_z варьируются в достаточно широком диапазоне. Они определяются элементами матрицы жесткости подсистемы инструмента, свойствами процесса резания, технологическими режимами и геометрией инструмента, влияющей на угловые коэффициенты.

Вначале рассмотрим случай, когда х1^,2 = Х2си ■ Возможность выполнения этого условия зависит от геометрии инструмента, которая определяет угловые коэффициенты, и углов ориентации осей эллипсов жёсткости в подсистеме инструмента, то есть от конструктивных свойств суппортной группы. Для этого случая наибольший интерес представляет выяснение влияния на свойства системы параметра р . Из (5) видно, что по мере увеличения р с учетом о           (Хз)2

соотношения _х^ = x₂ci,i существует точка бифуркации ро = с^ - — ₇с_ц, начиная с которой имеет место ветв-⁽Х1)

ление решений. Это бифуркация равновесия системы типа вилки. Ей соответствует С_Е = ⁰. Как видно, при [Зфо система имеет единственную точку равновесия (рис. 2, а). При Р)Ро свойства системы, рассматриваемые в вариациях относительно двух точек равновесия, например, ± X у, являются симметричными, как это наблюдается в системе Лоренца [19]. Не трудно показать, что для этой системы в потенциальной функции точкам ± X^ соответствуют два минимума. При Рф₀ потенциальная функция имеет единственный минимум, соответствующий точке X 2=0.

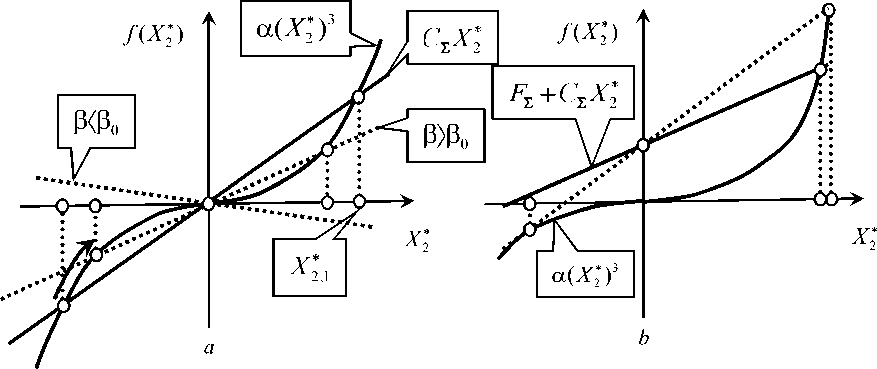
Рис. 2. Графическая интерпретация формирования точек равновесия системы: а ^— случай, когда ХА, 2 = Х2П.1;

14                                             ^{b —} случай, когда _Хлс_ХД * Х2НД

В общем случае условие хА,2 =Х2СЦ не выполняется. Тогда точка бифуркации и точки равновесия системы, во -первых, становится зависящими от F^, во-вторых, свойства системы в вариациях относительно точки равновесия b условие СЕ)0. Отметим, что точкам равновесия X2 из (4) однозначно соответствуют X1 -

Для анализа устойчивости точек равновесия необходимо рассмотреть линеаризованное в окрестности равновесия уравнение (3), получаемое после замены X , ( t ) = X 1 + x1 ( t ) и X ₂ ( t ) = X 2 + x ₂ ( t )

d ² x , dx        _п

т—h + hv--vcyx = 0, dt2      dt где т =

m

m

;

h

h 1,1-X1 p bT 1 ⁽¹⁾    h 2,1+3a T ₂⁽¹⁾( X ^ )²

, h 1,2"X2p bT 1 ⁽²⁾        h 2,2+ P T ₂ ⁽¹⁾

^{; c} x -

^c 1,1+X1 P b  ^c 2,1 -M X D²

^c 1,2+X2P b     ^c 2,2-P

.

Для анализа устойчивости конкретной точки равновесия необходимо рассматривать корни характеристического полинома системы (6)

А⁽ p ) =

^тР ² +⁽ h 1,1 -Х1Р ^bT 1 ⁽¹⁾⁾ P + c 1,1 +Х1Р ^b  [ h 2,1+3“ T 2 ⁽¹⁾⁽ X 2 ^)2] p + c 2,1 -За ⁽ X 2 ⁾²

^{( h} 1,2 -Х2Р bT!^ ) p + ^c 1,2 + X2P b

mp ² + ( h ₂,₂ + P T ®) p + c 2,2 ^_Р

-

Анализ эволюции корней характеристического полинома показывает большое разнообразие возможных меха-F ющее на X2, то знак смещения точки равновесия не влияет на свойства системы в вариациях относительно точки равновесия. Матрицы hE и сЕ в (6) являются несимметричными, то есть представимы в виде сумм симметричных и кососимметричных составляющих. Анализ конкретных систем показывает, что главным механизмом потери устойчивости равновесия связан с преобразованием симметричной составляющей матрицы hE из положительно определенной в отрицательно определенную. Кроме этого, по мере увеличения р возможно преобразование симметричной (потенциальной) составляющей матрицы с- из положительно в отрицательно определенную. При варьировании р и F^ имеют место множество бифуркаций многообразий, формируемых в окрестности равновесия.

Анализ бифуркаций системы - Проанализируем бифуркации системы на конкретном примере. При этом будем учитывать, что зачастую изучение примеров позволяет выяснить общие свойства. Так как при анализе бифуркаций необходимо рассматривать большие отклонения от точек равновесия, то для исследования необходимо рассматривать систему (3). Решение этой системы не может быть найдено в явном виде. Поэтому для ее интегрирования использовался метод Рунге -Кутта 4-го порядка.

m

0,2-10“2

0,2-10”2

; h =

1,2 0,8

0,8 2,0

; c =

800  900

900 1200

-

Размерность элементов матриц соответственно равна: [кг-с²/лш], [кг-с / мм], [кг/мм]. Они отличаются угловыми коэффициентами ориентации силы резания. Для системы №1 — _Х1 = 0,8 , _Х2⁼ 0,6 \ Для системы №2 — _Х1 = 0,6, _Х2 = 0,8. Таким образом, для системы №1 по мере увеличения р ветвление равновесия симметрично, симметричны и свойства в вариациях относительно точек равновесия. Для системы №2 имеет место асимметрия. Параметры процесса резания остаются неизменными и соответствуют: b = 3,0л/л/, а = 0,2лш, р = 2000кг/мм² , р = 0,9-104 кг/мм² , T ⁽¹⁾ = 0,002с, T² = 0,003с, T ₂⁽¹⁾ = 0,00 k, T ₂⁽²⁾ = 0,002с [12].

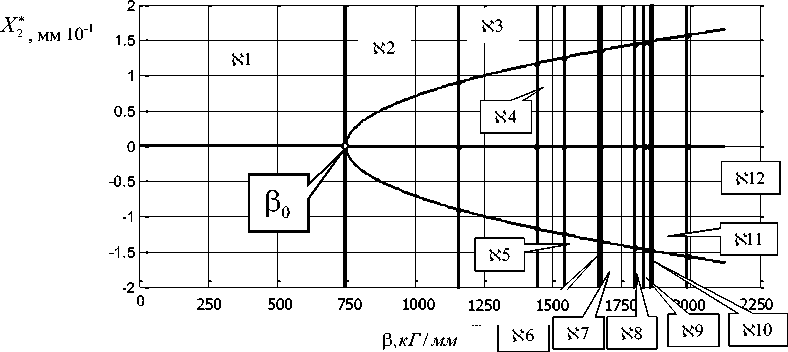
На рис. 3 приведены две диаграммы бифуркаций многообразий стационарного состояния в окрестности равновесия при варьировании Ре(0,2000)кг/лш. Проанализируем их по мере увеличения параметра р. Вначале проанализируем стационарные многообразия для системы № 1. По мере увеличения Р единственная точка равновесия является асимптотически устойчивой (множество К 1,р = [0-755]), затем имеет место бифуркация точки равновесия, при этом верхняя и нижняя точки двух ветвей диаграммы равновесия являются асимптотически устойчивыми (множество X2). Причем, устойчивость точек равновесия является апериодической. Затем (множество КЗ) наблюдается бифуркация Андронова-Хопфа рождения орбитально асимптотически устойчивой пары предельных циклов. Причем эти

Машиностроение и машиноведение

предельные циклы являются симметричными в окрестностях верхнего и нижнего равновесий. Они располагаются в ограниченном пространстве, расположенном между двумя верхними и нижними ветвями.

a )

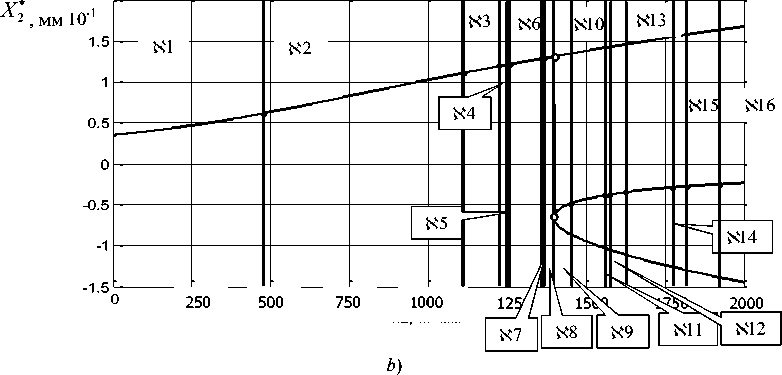
Рис. 3. Бифуркационная диаграмма при варьировании Р : ) F   0; b ) F ₌ *0

При дальнейшем увеличении Р (множество X4 ) наблюдается каскад бифуркаций удвоения периода. Известно, что бифуркация удвоения периода характеризует один из сценариев рождения хаотического аттрактора, рассмотренный М. Фейгенбаумом [25]. Хаотические аттракторы формируются на множестве X5 . Причем они образуются в окрестностях верхней и нижней точек равновесия, существуя в ограниченном объеме фазового пространства. Одновременно они характеризуют притягивающее многообразие. Далее, за счет увеличения интенсивности возбуждения, траектории становятся орбитальными относительно всех трех точек равновесия. При этом вначале формируется траектория с каскадом удвоения периодов (множество X6 ). Затем после каскада бифуркаций удвоения периода вновь формируется хаотический аттрактор (множество X9 ). Однако, в отличие от ранее рассмотренного хаотического аттрактора, траектории захватывают все три точки равновесия. В дальнейшем циклы преобразования стационарных траекторий периодически повторяются (множества N10, N11 ). Наконец, система становятся неустойчивыми в целом (множество N12 ). Однако в этом случае траектории, двигаясь относительно каждой точки равновесия, находятся в пространствах, которые не пересекаются друг с другом. Заметим, что, начиная с [3 = 1500 кг / л/л/свойства системы становятся чрезвычайно чувствительными к вариациям этого параметра.

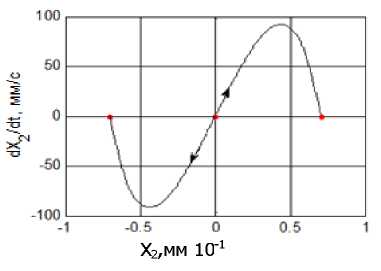
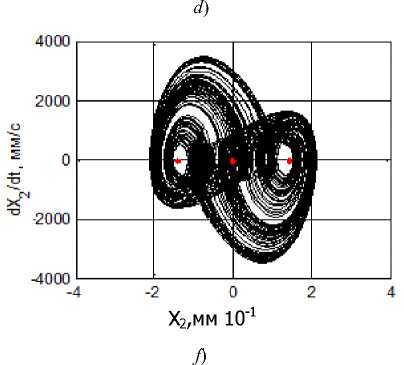
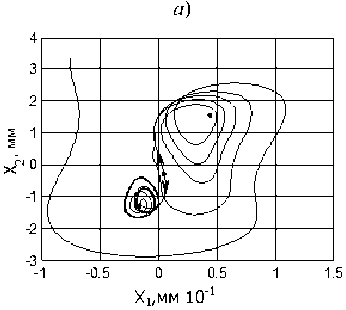
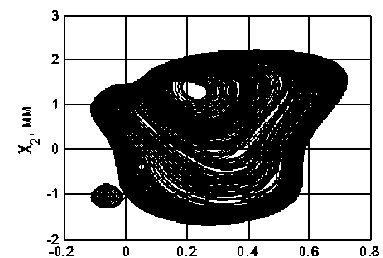
Некоторые наиболее типичные примеры проекций фазовых траекторий на плоскость X ₂ - dX ₂ / dt приведены на рис. 4. Здесь необходимо обратить внимание на то, что хаотические аттракторы при Р е К4 формируются исключительно в окрестности двух точек равновесия, а при р е К9 они напоминают аттрактор Лоренца и имеют свойства, близкие к этому аттрактору [23, 24].

Если F/ Ф0 (система № 2), то бифуркационная диаграмма за счет асимметрии верхней и нижней ветвей является более сложной. По мере увеличения Р система вначале также имеет единственную точку равновесия, которая является асимптотически устойчивой (множество N1 ). Затем, в окрестности единственной точки равновесия форми- руется устойчивый предельный цикл (множество X2 ), бифуркация удвоения периодов (множество X3 ), затем хаотический аттрактор (множество X4 ). Процесс удвоения периодов (множества X5и X7 ) и формирование хаотических аттракторов (множества X6и X8 ) повторяется вплоть до точки, в которой наблюдается ветвление равновесия Р0 1386кг / мм .

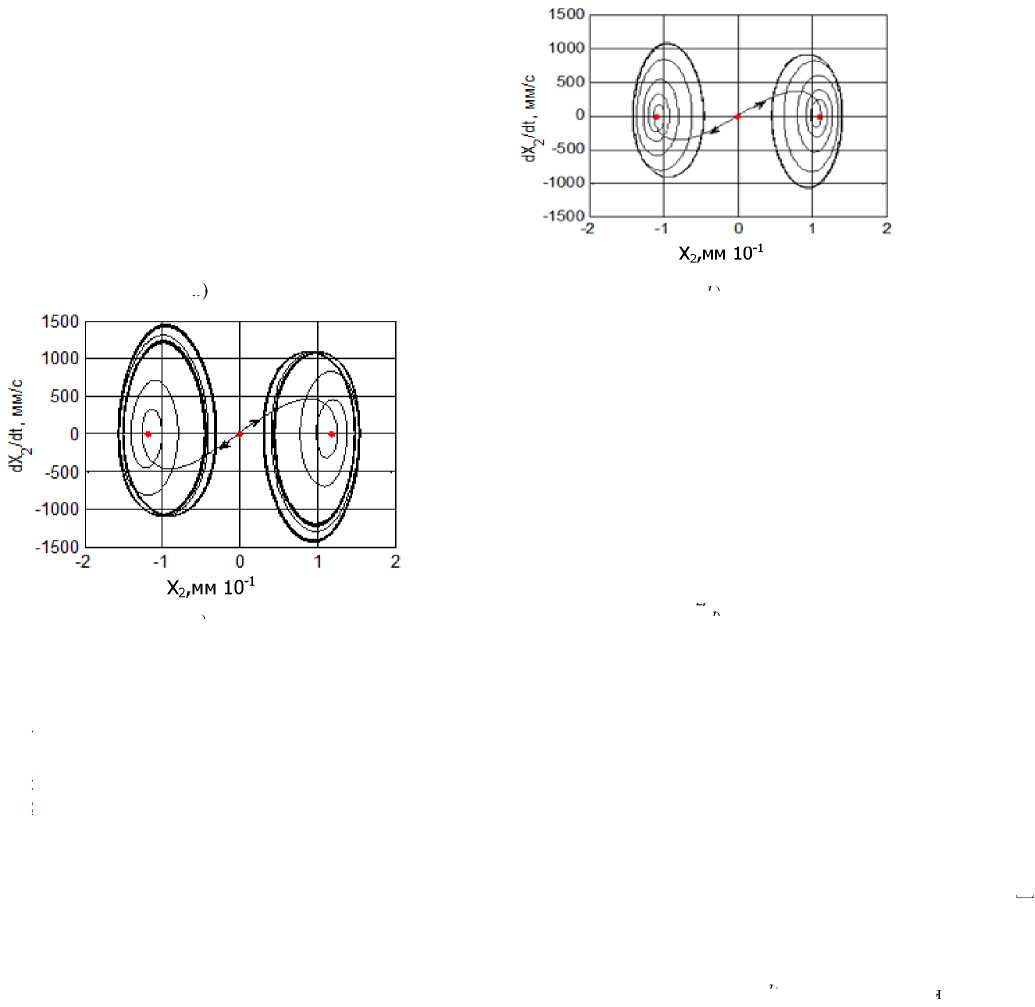
параметра Р для F 0 : a ) X 2 ; b )X 3 ; c ) X 4 ; d )X 5 ; e ) X 6 ; f ) X 9

)

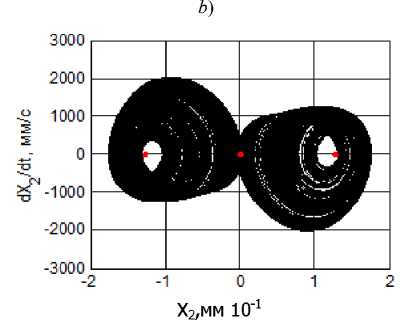
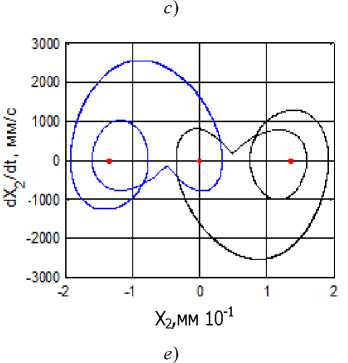
Рис. 4. Некоторые примеры проекций стационарных траекторий на фазовую плоскость X ₂, dX ₂/ dt по мере увеличения

Машиностроение и машиноведение

Затем свойства системы в окрестностях верхней и нижней ветви равновесия существенно меняются. Вначале в окрестности верхней ветви формируется странный аттрактор, а нижней — асимптотически устойчивая точка равновесия (множество К9 ). Затем в окрестности верхней ветви (множество N10 ) в системе вновь происходит бифуркация удвоения периода циклов, а на нижней — устойчивая точка равновесия. Наконец, в области нижней ветви наблюдается бифуркация Андронова–Хопфа (множество К11), в области верхней ветви продолжается процесс удвоения периода. При дальнейшем увеличении Р в области верхней ветви формируется хаотический аттрактор, а в области нижней ветви — сохраняются автоколебания (множество N12 ). Как предельный цикл, так и хаотический аттрактор характеризуют притягивающие стационарные многообразия, существующие в ограниченном фазовом пространстве. Наконец, в области верхней ветви система теряет устойчивость, и траектории уходят от центральной ветви, в области нижней ветви в ограниченном пространстве сохраняются автоколебания (множество X13 ). При дальнейшем увеличении Р система в области верхней точки равновесия остается неустойчивой, а в области нижней ветви в ограниченно про- 17

странстве вначале образуется каскад бифуркаций удвоения периода (множество N14 ), а затем образуется хаотический аттрактор, занимающий ограниченную область в окрестности нижней точки равновесия (множество N15 ). За пределами этой ограниченной области система движется по траекториям, отходящим от всех трех точек равновесия. Наконец, (множество N16 ) система становится неустойчивой в целом.

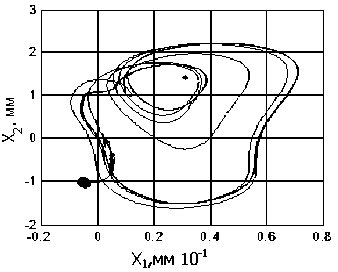
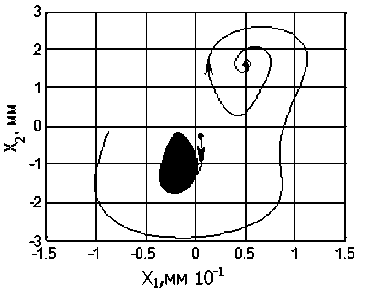
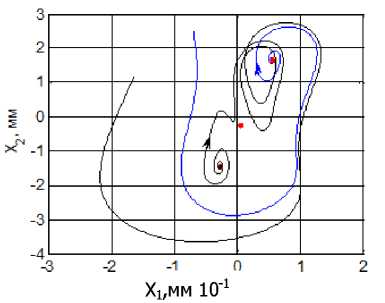
Принципиальным отличием каскада бифуркаций при F- #0 от системF0является различное поведение ее в областях верхней и нижней ветвей траектории смещения точек равновесия (рис. 5). При этом не образуются стационарные траектории, включающие сразу три точки равновесия, как это наблюдается в системе № 1. Обратим внимание на возможность существования в неустойчивой в целом системе некоторых локальных областей (рис. 5, с, d), в которых система является устойчивой в малом (рис. 5, с). Существуют также случаи, когда формируются хаотические аттракторы в ограниченном объеме (рис. 5, d). Цифровое моделирование показывает, что на формируемые многообразия, кроме Р и Fоказывают влияние практически все параметры системы (3). Если проранжировать параметры по чувствительности к ним изменения многообразий, то необходимо отметить существенное влияние постоянных врсмс ни в (3), которые моделируют запаздывание сил по отношению к деформационным смещениям. Именно через механизм влияния запаздывающих аргументов объясняется формирование многих стационарных многообразий, рассмот ренных выше.

Xi,mm 10"¹

b )

d )

е )

Рис. 5. Пример преобразования траекторий вершины инструмента в плоскости X ₁ - X ₂ по мере увеличения параметра Р для FV # 0: a )N11; b )N12; c )N14 ; d ) М15; e ) N16

Выводы. Динамическая система резания может служить примером сложных преобразований стационарных многообразий, формируемых в окрестности точек равновесия. В зависимости от параметров динамической характеристики процесса резания пространство состояния динамической системы резания структурируется, и при этом свойства системы становятся чувствительными к малым вариациям параметров. Характерными для системы являются бифуркации Андронова–Хопфа, удвоения периода колебаний и образование хаотических аттракторов. В рассматриваемой системе не обнаружено формирование многообразий типа инвариантного тора. Необходимо подчеркнуть, что все эти преобразования имеют практическое подтверждение, экспериментально полученное нами и другими исследователями [11, 29]. Если принять во внимание, что система резания является возмущенной, то в ней в реальных условиях образуется сложный, трудно предсказуемый режим колебаний. Важно подчеркнуть, что эти колебания оказывают влияние на параметры качества изготовления деталей.