Однокомпонентный сферический датчик напряженности электрического поля с разомкнутой системой электродов в поле вблизи заземленной проводящей плоскости

Работы, направленные на исследования, создание и проектирование датчиков и средств измерений напряженности низкочастотного электрического поля (ЭП), всегда актуальны. Такие средства измерений используются для измерения и контроля ЭП промышленной частоты 50 Гц. Измерения проводятся на рабочих местах и территориях с установленным сверхвысоковольтным оборудованием. Целью инструментального контроля является гигиеническая оценка условий труда обслуживающего персонала.

Используемые на сегодняшний день средства измерений напряженности ЭП, содержащие сферические датчики напряженности ЭП электроин-дукционного типа с замкнутой системой чувствительных электродов (ЧЭ), хорошо представлены в работах [1–8]. Данная работа является следующей в цикле работ по исследованию нового типа электроиндукционных сферических датчиков, имеющих разомкнутую систему ЧЭ, представляющих собой полые сферические сегменты. Предыдущая работа автора посвящена исследованию поведения датчиков с разомкнутой системой электродов в однородном поле [9]. В данной работе будет рассмотрено поведение датчика ЭП в условиях присутствия проводящей заземленной плоскости. Подобная задача решалась в работе [10] для ЧЭ в форме сплошных сферических сегментов. В этой работе рассмотрен частный случай для сферических сегментов, представляющих сплошные полусферы.

ПОСТАНОВКА ЗАДАЧИ

Провести теоретические исследования поведения однокомпонентного сферического электроин-дукционного датчика напряженности ЭП с ра- зомкнутой системой проводящих электродов в электрическом поле с заземленной проводящей плоскостью. Для этого необходимо:

• 1)    построить краткую теорию взаимодействия датчика, находящегося в ЭП с заземленной проводящей плоскостью;

• 2)    построить математическую модель взаимодействия датчика с ЭП с заземленной проводящей плоскостью;

• 3)    провести математическое моделирование, по результатам которого установить влияние заземленной проводящей плоскости на электрические параметры датчика, такие как электрический заряд, индуцированный на электродах датчика, напряжение холостого хода и электрическая емкость между электродами датчика;

• 4)    оценить погрешность датчика по межэлектродной емкости, электрическому заряду и напряжению холостого хода;

• 5)    сделать заключение по полученным результатам.

ТЕОРИЯ

Решения поставленных задач будет связано с рассмотрением поведения электроиндукционного сферического датчика напряженности ЭП с разомкнутой системой электродов при работе в поле вблизи заземленной плоскости. Для этого решим следующую задачу. Разместим находящиеся над проводящей заземленной плоскостью две проводящие сферические оболочки в форме сфериче- ских сегментов, лежащих на поверхности виртуальной сферы радиуса R. Сферические сегменты будут являться ЧЭ датчика. Обозначим поверхности первого и второго сферических сегментов через S1 и S2, их размеры зададим углом θ0 и текущее угловое значение углом θ. Примем расстояние от центра виртуальной сферы до плоскости равным d. Рассматриваемая в задаче ситуация представлена на рисунке.

Воспользуемся коллективными фундаментальными работами [11–14] и работами отдельных авторов [15–17] и выделим из них основные теоретические положения, необходимые для расчета датчиков с разомкнутой системой электродов, находящихся в поле заземленной плоскости. Обоснуем основные электрические параметры датчика, которые должны определять выделенные теоретические положения.

Для решения задачи зададим исходное положение сферического датчика в ЭП с проводящей плоскостью. Обозначим буквой d расстояние от центра датчика до проводящей плоскости, имеющей координату z = 0. При нахождении описанной системы ЧЭ в ЭП с заземленной плоскостью на их поверхностях S 1 и S 2 индуцируются противоположные по знаку электрические заряды – q 1 и + q 2 . Под действием ЭП электроды датчика 1 и 2 приобретут электрические потенциалы ϕ 01 и ϕ 02 , связанные с электрическими зарядами через межэлектродную емкость C , являющуюся емкостью C Д датчика. Электрические заряды и потенциалы электродов датчика пропорциональны напряженности ЭП.

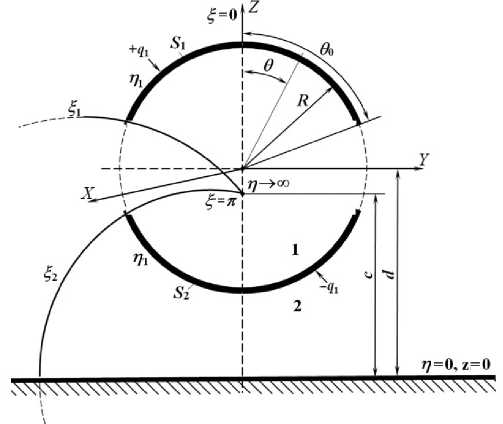
Рис. Система сферических электродов для исследования датчика в электрическом поле заземленной плоскости.

Основные характеристики: S 1 , S 2 — ЧЭ датчика, R — радиус виртуальной сферы, d — расстояние от датчика до заземленной плоскости, θ ₀ — угловой размер ЧЭ

Следовательно, основными электрическими параметрами датчика будут являться электрические заряды q , потенциалы ϕ и емкость C Д . На их определение будут нацелены разрабатываемые теоретические положения.

Решим в нашей ситуации (см. рис.) краевую задачу для уравнения Лапласа. Для этого зададим граничные условия в виде

• ^A ^ = 0; й|s 1 = й и; ^| s 2 = й й; й| z = 0 = 0, ⁽¹⁾ где S 1 и S 2 — поверхности электродов 1 и 2 соответственно; ϕ 01 , ϕ 02 — заданные граничные условия. Решение будем проводить методом парных интегральных уравнений [9].

Для удобства решения задачи введем бисфери-ческую систему координат ( ξ , η , θ ) [18, гл. 2]–[20] (см. рис.). Из [1] — следующая связь бисфериче-ских координат с декартовыми координатами:

где с — расстояние от плоскости до первого фокуса бисферической системы координат, второй фокус находится под плоскостью на таком же расстоянии; n — изменяется от да до - да ; £ — в пределах 0 <  £ < п ; 0 — изменяется в пределах 0 <  0 <  2 п (см. рис.); ch n и sh n — гиперболические косинус и синус.

Выполняя граничные условия (1) и воспользовавшись известным [12] выражением q = f °( S )d S, S

найдем электрические заряды на электродах 1 и 2. Для этого необходимо проинтегрировать поверх- ностную плотность зарядов дй °(S) = s~ dn

n =n 1

по поверхностям S1 и S2 электродов 1 и 2. Тогда получим:

c • sin £ • cos в ch n - cos £ c • sin £ • sin в ch n - cos £ c • sh n chn- cos£

t Ш\

£ 1     cos—sh—

q1 = 8nsd[f(t) —2---2- d t, ch n - cos t

\              ⁰              1                                   (4)

tη n sin — ch — q2 = -8nsd \ f (t)---2----— dt,

2          { 72 chn1 - cost где f1(t) и f2(t) — функции [12], получаемые из решения системы парных интегральных уравнений:

ξ 1

f l (в 0 ) --f f l ( в )

π ₀

π

- -f f 2( в ) x ^π ξ 2

f в + в ^ u cos I — 2 J sh n 1 ch2 n 1 - cos( e + в ₀ )

( в - в ^ u cos I —2   J sh n 1

ch2 n 1 - cos( e - в ₀ )

. f в + в ] u ■ ( в - в ] u sin [ — 2    J sh n i sin I — J sh n 1

ch 2n_t - cos( в + в ₀ ) ch 2n - cos( в - в ₀ )

π fв --f f2(в)

π

ξ ₂

ξ 2

- -J f l ( в ) x

π ₀

в - в u cos ⁰ sh η ₁ -----²-------- +

π d в + — ff2в)

2 π

ξ ₂

4 d в = - Ф ₍ π

f в + в ), cos I —2 J sh n 1

ch 2 n 1 - cos( в - в ₀ ) ch 2 n 1 - cos( в + в ₀ )

f в+в          f в - в sm I —2  J sh n1   sm I —2 J sh n1

ch 2 n 1 - cos( t + x ) ch 2 n 1 - cos( t - x )

d θ

. „ 4

d в = - Ф 02 π

. в + в sin 0

-

3 θ

2ch n ! - cos ^0 - 3

2 a (ch n 1 - cos в ₀ )

+ —

2 π

ξ 2

J f l ( ^в )

- в + в sin 0

3 θ

2ch n 1 - sin     - 3

2 a (ch n 1 - cos в ₀ )

,

■ в - в sin ⁰

;

-

- в - в sin 0

d в -

d в -

где a = R / d — относительное расстояние от центра датчика до заземленной плоскости; R — радиус сферического электрода; d — расстояние от центра датчика до заземленной плоскости; Ф 01 и Ф ₀₂ — потенциальные функции ЧЭ 1 и 2 датчика в поле заземленной плоскости, определяемые из системы парных интегральных уравнения (5), (6).

Потенциальные функции Ф 01 и Ф 02 соответственно равны

Ф 01 = Ф 0О1 •

Ф 02 = ^Ф •

θη sin — • ch— ch n1 - cos t

θη sin — • ch — ch n1 - cos 90

= E 0 R

θη sin — • ch —

= E 0 R

ch n 1 - cos t ’

θη sin— • ch — ch n1 - cos90 ’

Целесообразность рассмотрения дифференциального электрического заряда, а не зарядов q 1 и q 2 в отдельности заключается в том, что в однородном поле q 1 = |— q ₂| , а в неоднородном поле q 1 ^ I- q ₂| , поэтому сложно оценить их измерения, вызванные неоднородностью поля.

Полученные автором выражения (3)–(11) при формировании краткой теории взаимодействия однокомпонентного сферического датчика напряженности ЭП, имеющего разомкнутую систему ЧЭ, с полем с проводящей плоскостью будут положены в основу математической модели датчика, используемой для дальнейших исследований.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

И ЕГО РЕЗУЛЬТАТЫ

где Ф ₀ ^О ₁ и Ф ₀ ^O ₂ — потенциальные функции ЧЭ 1 и 2 датчика в однородном ЭП, определяемые из системы парных интегральных уравнений, полученных для однородного поля. В обозначении потенциальных функций "О" означает потенциальные функции в однородном поле; a = R / d — пространственный диапазон измерений; R — радиус датчика; d — расстояние до источника поля.

Решение системы парных интегральных уравнений (5), (6) способствует нахождению функций f 1 ( θ 0 ) и f 2 ( θ 0 ), по которым определяются электрические заряды (4), индуцированные полем на поверхностях ЧЭ датчика, и электрическая емкость, создаваемая ЧЭ [11]

θ 0

r¹             0

C = ⁿR ^{1 - 2} J f (⁹ )_sm-d ⁹ .

Электрические потенциалы ϕ ₀ ^Н ₁ и ϕ ₀ ^Н ₂ (Н в обозначении означает потенциал в неоднородном поле) ЧЭ 1 и 2 определятся через найденные по выражениям (4) электрические заряды q 1 и q 2 датчика и его емкость (8)

Н    q 1        Н    q 2

@ 01   C  и @ 02    C

.

Найденные выражения (4) для электрических зарядов, индуцированных на ЧЭ датчика, и их потенциалов (9) позволяют определить:

– дифференциальный электрический заряд

a q = q i ^- q - ,                   ⁽¹⁰⁾

– разность потенциалов ЧЭ датчика, соответственно равную напряжению холостого хода

HH

U xx = @ 01   @ 02 -

Для проведения математического моделирования построена математическая модель, объединяющая выражения (3)–(11). Математическая модель позволяет задавать конструктивный размер θ 0 ЧЭ датчика и пространственное расстояние d от центра датчика до заземленной плоскости. Пространственное расстояние задавалось через относительное расстояние (пространственный диапазон измерения) a = R / d .

Задавая различные значения угловых размеров ЧЭ θ 0 и относительного расстояния a , при математическом моделировании:

– определялись электрические параметры датчика, такие как межэлектродная емкость C , дифференциальный заряд ЧЭ A q и напряжение холостого хода U xx ;

– оценивались изменения указанных параметров, вызванные приближением датчика к заземленной плоскости.

Математическое моделирование проводилось для датчиков с ЧЭ в форме полых сферических сегментов с изменением их угловых размеров 9 от 30 ° до 90 ° с шагом в 15 ° и в пространственном диапазоне a , изменяющимся в интервале 0 <  a <  1 с шагом 0.1.

При моделировании были приняты следующие нормировки: A q * =A q/ ( ns ₀ R²E ₀ ) — для дифференциального заряда; U *x = U xx/ R • E о — для напряжений холостого хода; C* = С /( 4ns ₀ R ) — для электрической емкости, где s = 8.85Л0^-12 Ф/м — электрическая постоянная; E 0 — напряженность однородного ЭП при a → 0.

Результаты математического моделирования в виде численных значений искомых параметров представлены в таблице.

Табл. Расчетные значения электрических характеристик датчика при его работе в поле с заземленной плоскостью в зависимости от его конструктивных параметров и высоты над плоскостью

Угол ЧЭ 0 0	й й S Ь S ей X г; Г)	Высота над плоскостью a = R / d
		~0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
30 °	C*	0.1961	0.1963	0.1965	0.1973	0.1981	0.2001	0.2042	0.2123	0.2240	0.2471	0.2971
	X a ), %	0	0.14	0.28	0.55	0.98	1.82	4.22	8.08	14.34	26.08	51.35
	A q*	1.433	1.435	1.438	1.442	1.449	1.461	1.497	1.555	1.649	1.828	2.222
	γ ( a ), %	0	0.16	0.32	0.61	1.08	1.98	4.48	8.51	15.10	27.59	54.89
	U * xx	1.8238	1.8242	1.8245	1.8249	1.8260	1.8270	1.8280	1.8311	1.8360	1.8460	1.8665
	8( a ), %	0	0.02	0.04	0.06	0.1	0.157	0.25	0.4	0.67	1.2	2.34
45 °	C*	0.3201	0.3203	0.3210	0.3221	0.3242	0.3271	0.3333	0.3452	0.3613	0.3931	0.4353
	X a ), %	0	0.08	0.29	0.62	1.16	2.14	4.04	7.93	12.86	22.21	41.53
	A q*	2.052	2.055	2.059	2.067	2.080	2.104	2.148	2.238	2.358	2.589	2.920
	γ ( a ), %	0	0.12	0.35	0.73	1.36	2.52	4.69	9.08	14.90	26.17	48.28
	u* xx	1.6053	1.6059	1.6063	1.6072	1.6084	1.6112	1.615	1.6225	1.6341	1.6485	1.6769
	0( a ), %	0	0.04	0.06	0.11	0.2	0.36	0.63	1.07	1.81	3.24	4.77
60 °	C*	0.4851	0.4852	0.4860	0.4880	0.4901	0.4951	0.5021	0.5120	0.5323	0.5781	0.6452
	^ ( a ), %	0	0.044	0.208	0.624	1.068	1.973	3.461	5.538	9.767	19.378	33.06
	A q*	2.582	2.585	2.591	2.602	2.618	2.649	2.699	2.768	2.905	3.221	3.729
	γ ( a ), %	0	0.1	0.32	0.78	1.37	2.58	4.51	7.21	12.54	24.8	44.41
	U * xx	1.3319	1.3322	1.3332	1.3340	1.3359	1.3396	1.3452	1.3533	1.3660	1.3920	1.4450
	8( a ). %	0	0.05	0.11	0.15	0.3	0.59	1.05	1.58	2.49	4.5	8.53
75 °	C*	0.7201	0.7201	0.7211	0.7230	0.7252	0.7301	0.7341	0.7392	0.7561	0.8050	0.9021
	X a ), %	0	0	0.13	0.38	0.75	1.4	1.89	2.68	4.93	11.74	25.27
	A q*	2.894	2.897	2.906	2.917	2.937	2.969	3.004	3.066	3.209	3.545	4.118
	γ ( a ). %	0	0.13	0.43	0.82	1.48	2.62	3.83	5.97	10.91	22.52	42.31
	xx.	1.0052	1.0062	1.0080	1.0100	1.0131	1.0172	1.0239	1.0371	1.0622	1.1020	1.1423
	0( a ), %	0	0.12	0.3	0.43	0.73	1.2	1.9	3.2	5.7	9.65	13.6
90 °	C*	1.558	1.559	1.560	1.561	1.562	1.565	1.570	1.580	1.597	1.616	1.637
	X a ), %	0	0.06	0.12	0.19	0.26	0.45	0.77	1.41	2.50	3.72	5.04
	A q*	3.003	3.012	3.02	3.034	3.053	3.086	3.148	3.295	3.564	4.348	6.477
	γ ( a ), %	0	0.29	0.58	1.03	1.65	2.76	4.82	7.83	13.07	22.75	43.81
	U * xx	0.482	0.483	0.484	0.486	0.488	0.493	0.498	0.511	0.528	0.567	0.651
	8( a ), %	0	0.21	0.42	0.83	1.45	2.28	3.3	6.02	9.54	17.64	35.06

По численным значениям таблицы были рассчи- Поскольку эти характеристики выступают здесь как таны изменения электрических характеристик C*, результаты измерений поля, то уместно трактовать Aq * и U*xx., вызванные влиянием проводящей плос- их изменения как погрешности измерений кости при приближении датчика к ее поверхности.     β(а) = [x(a) – x(~0)] / x(~0) × 100%, где β(а) — погрешности электрических параметров x(): C(а), Aq*(а) и U*xx(а), соответственно обозначенные в таблице, как ^( a), у( a) и £ a).

Результаты расчетов занесены в ту же таблицу. Из данных таблицы следует, что емкость C ^*, дифференциальный электрический заряд A q и напряжение холостого хода U ^*_xx увеличиваются по мере приближения к заземленной плоскости. Наибольшее увеличение наблюдается для емкости C ^* и дифференциального электрического заряда A q , наименьшее — для напряжения холостого хода U ^* xx . Это подтверждают и рассчитанные значения погрешности этих параметров.

Значительное увеличение

– емкости C ^* объясняется "открытостью" электродной системы датчика, на которую оказывают влияние проводящая заземленная плоскость и внешние тела;

- дифференциального электрического заряда A q объясняется, тем, что его погрешность Ya ) пропорциональна сумме погрешностей ^ ( a ) межэлектродной емкости и £ a ) напряжения холостого хода, т.е. / ( a ) ~ [ ^ ( a ) + ц ( a ) ] .

Незначительное увеличение напряжения холостого хода U ^* xx объясняется, тем, что его погрешность . £ a ) пропорциональна разности погрешностей Ya ) дифференциального электрического заряда и межэлектродной емкости ^ ( a ), т.е. £ ( ^а ) ~ [ / ( ^а ) — 0( a ) ] • Это еще раз подтверждает правильность выбора в ранней работе автора [9] в качестве выходного параметра напряжения холостого хода.

При выходном сигнале датчика в виде напряжения холостого хода и выборе углового размера ЧЭ датчика 0 0 <  45 ° погрешность датчика, вызванная влиянием проводящей плоскости, не превысит £ a ) <  4.77% в пространственном диапазоне 0 <  a <  1, а в допустимом пространственном диапазоне 0 <  a <  0.5 не превысит £ a ) <  0.36%.

Допустимый пространственный диапазон измерения исключает касание датчиком заземленных и токоведущих тел. В допустимом диапазоне a = = R / d <  0.5, т.е. расстояние между центром датчика и внешними телами не должно быть меньше d = 2 R , а просвет не должен быть меньше R .

Таким образом, результаты, полученные при математическом моделировании датчика с разомкнутой системой электродов, подтвердили возможность его использования вблизи заземленной плоскости.

ВЫВОДЫ И ЗАКЛЮЧЕНИЕ

Выводы по результатам исследований сводятся к следующему.

• 1)    Построена краткая теория поведения однокомпонентного датчика напряженности ЭП с разомкнутой системой электродов в форме полых сферических сегментов вблизи проводящей заземленной плоскости.

• 2)    Составлена математическая модель датчика, учитывающая конструктивные параметры ЧЭ датчика и параметры, задающие пространственное положение датчика относительно заземленной плоскости. В основу математической модели датчика легли основные уравнения краткой теории.

• 3)    Проведено математическое моделирование датчика, позволившее получить численные значения межэлектродной емкости C ^*, дифференциального электрического заряда A q ^* и напряжений холостого хода U ^* xx в зависимости от пространственного диапазона измерения датчика a и угловых размеров его ЧЭ 0₀. При этом пространственный диапазон измерения изменялся в диапазоне 0 <  a <  1 с шагом 0,1, а угловой размер сферических сегментов 0₀ — от 30 ° до 90 ° с шагом в 15 ° .

• 4)    Установлено, что при приближении к проводящей плоскости наиболее сильно изменяются такие параметры датчика, как межэлектродная емкость C ^* и дифференциальный электрический заряд A q ^*, индуцированный на электродах датчика.

• 5)    Установлено, что минимальную погрешность, вызванную приближением датчика к проводящей плоскости, обеспечивает напряжение холостого хода U ^* xx , принятое за выходной сигнал датчика.

• 6)    Установлено, что напряжение холостого хода при угловом размера ЧЭ датчика 0 0 <  45 ° , обеспечит датчику погрешность, вызванную влиянием проводящей плоскости, не превышающую S( a ) <  4.77% во всем пространственном диапазоне измерения 0 <  a <  1.

• 7)    Показано, что при тех же угловых размерах ЧЭ датчика, но в допустимом пространственном диапазоне 0 <  a <  0.5 погрешность датчика не превысит £ ( a ) <  0.36%.

• 8)    Подтверждена возможность применения датчика вблизи проводящей заземленной плоскости.

Подытоживая результаты проведенных исследований, можно заключить, что получены новые сведения о поведении датчика напряженности ЭП с разомкнутой системой электродов, находящимся в однородном поле вблизи заземленной плоскости.