Одномерная модель удлинения нитей основы в тканом полотне с учетом сил трения

УДК 620.19:677.017:53.09                              

Важнейшую, если не основную, роль во взаимодействии волокон в пряже, а нитей основы и утка, ‒ в ткани, играют силы трения и сцепления. Их принято относить к разновидности трения, называемого «сухим» трением, и описывать обобщенным законом Кулона – Амонтона [1]. Движение или покой взаимодействующих по этому закону тел описываются уравнениями механики, которые являются нелинейными, плохо поддающимися линеаризации. Поэтому адекватное включение поля сил сухого трения, например, в конечно-элементную модель проблематично. Как было доказано в [2], при квазистатических нагрузках наличие большого числа участков трения в материале со статистическим разбросом значений нормальных давлений, площадей контакта и коэффициентов трения и сцепления происходит нивелирование нелинейного закона Кулона – Амонтона и преобразование его в закон вязкого трения, в котором сила трения линейно связана со скоростью деформации.

Для оценки роли сил трения при деформации тканого полотна рассмотрим упрощенную модель деформации нити основы при удлинении образца ткани. Геометрическая схема модели представлена в верхней части рисунка 1. На участках перекрытия основы и утка происходит уменьшение передаваемой по основе силы натяжения T(k) из-за противодействующих сил трения. В идеализированной форме для тонких нерастяжимых нитей, огибающих криволинейную поверхность, это уменьшение описывается формулой Эйлера T(k) = T(k-1) exp(-p а), где к - номер уточной нити, который отсчитывается от подвижной кромки образца; μ – коэффициент трения, α – угол охвата нитью криволинейной поверхности. В рассматриваемом случае формула может быть применена к тем волокнам основной нити, которые на участке перекрытия неподвижны относительно утка и охватывают его на участке перекрытия. Та часть волокон основы, которая непосредственно не взаимодействует с утком, находится в тесном взаимодействии с окружающими их волокнами за счет уплотнения сечений основы на участках перекрытия. Поэтому их также можно считать неподвижными относительно уточной нити и распространить и на них применение формулы Эйлера. Поскольку поперечное сечение нитей основы соизмеримо с радиусом кривизны, а нити содержат большое число волокон или элементарных нитей, и само сечение далеко от идеализированной формы вследствие расплющивания при формировании элемента переплетения, то формула Эйлера применима с определенными оговорками. Существуют и другие важные особенности деформации основной нити при удлинении образца ткани вдоль основы.

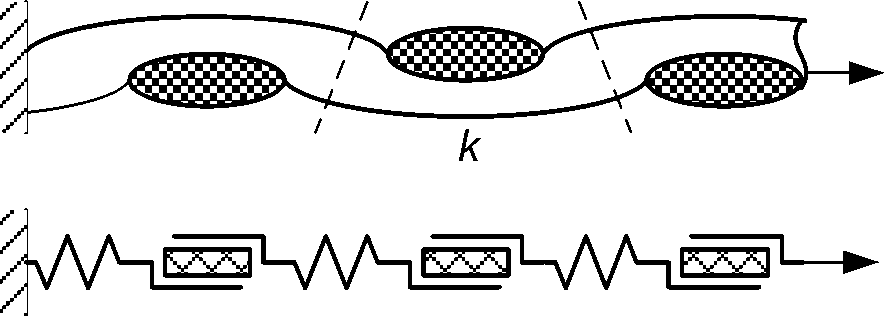
Рисунок 1 ‒ Геометрическая схема и механическая модель удлинения нити основы при растяжении образца тканого полотна. Чередование упругих элементов и элементов с сухим трением

Участки основной нити, направленные вдоль действия растягивающей нагрузки, приходятся на перекрытия с нитями утка. Взаимодействие с утком упрочняет нить основы. Части основной нити, приходящиеся на участки между перекрытиями, находятся под большими углами в к плоскости ткани. Поэтому деформация этих частей нити относительно невелика. Эти особенности в целом приводят к увеличению прочности ткани и увеличивают ее сопротивление удлинению. Перечисленные специфические особенности можно приближенно учесть, уменьшив эффективное значение коэффициента трения. Учитывая, что в каждом перекрытии эти изменения имеют случайные вариации, примем, что эффективное значение коэффициента трения равно ц_э = z Ц, где z - равномерно распределенное случайное число. Каждый элемент ткани, включающий в себя участок перекрытия основной и уточной нитей и участок основы между соседними уточинами, описывается следующими соотношениями

T(k) = T(к -1) ■ exp(- Це(к) • а(к))

AL(к) = T(k)' L(k) • cos(^(к)) к = 1,2,...,N E (к) • 5 (к)

В этих формулах: T(к) - натяжение нити основы в к-м элементе перекрытия; це(к) - значение эффективного коэффициента трения между волокнами основной нити и волокнами утка; а(к) - угол охвата нитью основы уточной нити на участке перекрытия; AL(к) -величина абсолютного удлинения основной нити в пределах к-го элемента перекрытия в плоскости тканого полотна; L(к) - длина нити основы в пределах к-го элемента перекрытия; E(к) и S(к) - соответственно, модуль упругости и площадь поперечного сечения основной нити; в(к) - угол наклона нити основы к плоскости полотна в соответствии с фазой строения переплетения. Все перечисленные величины, входящие в формулы, зависят от номера элемента перекрытия, поскольку они могут варьировать в некоторых, иногда весьма значительных пределах, от элемента к элементу из-за влияния различных случайных факторов.

Для моделирования удлинения нити основы была построена компьютерная программа [3, 4], выполняющая вычисления в соответствии с приведенными формулами рекуррентно для каждого элемента полотна. Исходные данные, использованные при расчетах: длина моделируемого образца 0,2 м; плотность ткани по утку 400 нитей на дециметр; толщина основной и уточных нитей принята одинаковой и равной 30 текс; модуль упругости 240 9 Ра, что соответствует нейлону; среднее значение коэффициента трения 0,26; углы охвата основной нитью уточной нити и наклона основной нити к плоскости ткани соответственно 140 и 60 градусов.

На графиках рисунка 2 показаны кривые изменения относительного удлинения нити основы и относительной накопленной деформации в зависимости от номера элемента. Кривые получены для трех вариантов моделей. В первом варианте среднее значение коэффициента трения равно 0,26 с равномерно распределенными случайными вариациями между элементами перекрытия в пределах ± 0,03. Во втором варианте случайная составляющая вариации исключена, а коэффициент трения равен среднему значению. В третьем варианте случайная составляющая коэффициента трения также отсутствует, но значение увеличено до 0,33. В соответствии с этими вариантами на рисунке относительные удлинения обозначены: и для первого варианта; uSr для второго варианта и иМ для третьего варианта. Аналогично, накопленные по длине образца относительные удлинения обозначены us, usSr и usM . В качестве аргумента в графиках всех этих зависимостей использованы не номера элементов k , а их отношения к общему числу уточных нитей в моделируемом образце Nk .

Кривые на рисунке 2 показывают, что, несмотря на заметные случайные вариации относительной деформации нити основы от элемента к элементу, относительная накопленная деформация нивелирует эти вариации и может быть хорошо аппроксимирована экспоненциальной зависимостью.

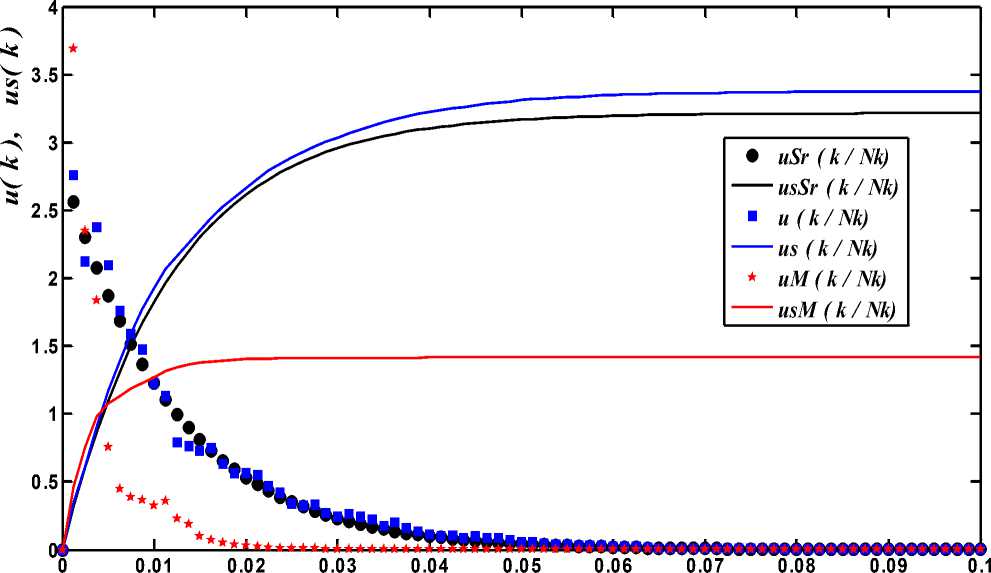
k / Nk

Рисунок 2 ‒ Изменение относительной деформации нити основы по длине растягиваемого образца тканого полотна

Таким образом, моделирование показало, что деформация удлинения распространяется не по всей длине образца полотна равномерно, а постепенно ослабевает от той части образца, к которой она непосредственно применяется, к удаленной части образца. Напряжение в нити также ослабевает за счет сил трения по мере удаления участка от места приложения нагрузки. Вместе с тем случайные вариации величин от одного к другому элементов перекрытия не существенны для распространения деформации и напряжения и могут быть исключены из рассмотрения, что упрощает модель.

Аналогичные выводы можно получить и с помощью конечно-элементной модели основной нити в растягиваемом образце ткани. В основу геометрической модели при конечно-элементном моделировании нити основы использованы геометрическая модель нити основы и схема структуры ее взаимодействия с нитями утка, изображенная на рисунке 1. Для имитации взаимодействия нити основы с уточными нитями задавались граничные условия в виде чередующихся по направлению действия сил, направленных перпендикулярно оси нити основы в пределах полуволн только на участках ее взаимодействия с нитями утка. Для имитации сил трения задавались силы, направленные в сторону, противоположную деформации, и действующие по объему нити основы в пределах взаимодействия с уточными нитями. Амплитудные значения этих сил обозначим A усл. ед., а коэффициент трения µ.

На рисунке 3 представлены полученные с помощью этой модели эпюры первого главного компонента тензора деформации epx для трех вариантов моделирования. В первом варианте силы взаимодействия с уточными нитями отсутствовали, и силы трения были «выключены», т.е. нить моделировалась как абсолютно упругий, прямолинейный стержень, удлиняемый на 10 % своей длины. При этом, за исключением краев нити, деформация распределена равномерно по длине. Во втором варианте «включены» силы поперечного воздействия (изгиба) нити под действием нитей утка, что привело к изгибу основы и возникновению периодических изменений в величине деформации по длине нити. В третьем варианте, кроме изгибающих поперечных воздействий, на нить основы действуют также силы трения, распределенные по ее объему на участках взаимодействия с нитями утка. При этом деформация нити основы сосредоточена у конца, к которому приложена удлиняющее воздействие. На зажатом и неподвижном конце нити деформация принимает малые значения. Это подтверждает вывод о том, что трение в нити основы, как между ее волокнами, так и о нити утка, приводит к перераспределению деформации и напряжений по длине нити основы, а значит, и по длине образца ткани.

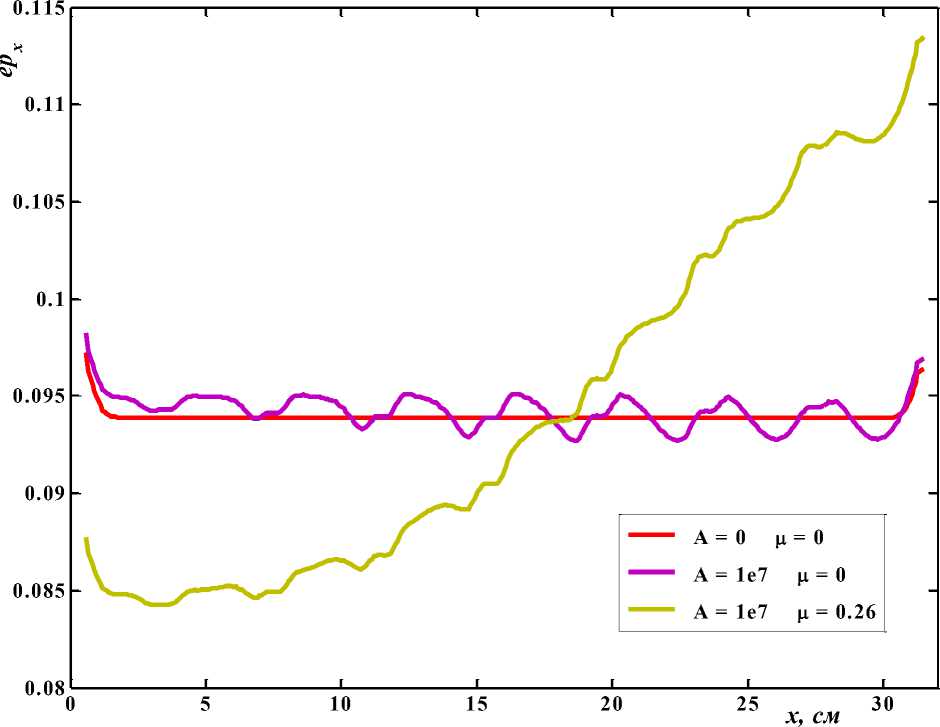
Рисунок 3 ‒ Диаграмма распределения главного компонента тензора деформации по длине основной нити при отсутствии сил трения для трех вариантов конечно-элементного моделирования