Одномерный фотонный кристалл на основе нанокомпозита: металлические наночастицы - диэлектрик
Автор: Дьяченко П.Н., Микляев Ю.В.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 1 т.31, 2007 года.
Бесплатный доступ
В работе исследован одномерный фотонный кристалл на основе нанокомпозита: металлические наночастицы - диэлектрик. Предсказано возникновение эффекта расщепления единой зоны на поляритонную и структурную фотонную запрещенную зону. Найдено различие в поведении структурной фотонной запрещенной зоны при изменении концентрации металлических наночастиц, в зависимости от ее положения относительно поляритонной фотонной запрещенной зоны. Рассмотренные эффекты позволяют расширить возможности создания новых фотонных кристаллов с заданными свойствами.
Короткий адрес: https://sciup.org/14058728
IDR: 14058728
Текст научной статьи Одномерный фотонный кристалл на основе нанокомпозита: металлические наночастицы - диэлектрик
В работе исследован одномерный фотонный кристалл на основе нанокомпозита: металлические наночастицы - диэлектрик. Предсказано возникновение эффекта расщепления единой зоны на поляритонную и структурную фотонную запрещенную зону. Найдено различие в поведении структурной фотонной запрещенной зоны при изменении концентрации металлических наночастиц, в зависимости от ее положения относительно поляритонной фотонной запрещенной зоны. Рассмотренные эффекты позволяют расширить возможности создания новых фотонных кристаллов с заданными свойствами.
Фотонными кристаллами называют структуры, с периодической модуляцией показателя преломления, обладающие фотонной запрещенной зоной (ФЗЗ) [1]. Уже в 1972 г. в работе Быкова [2] было показано, что такие структуры позволяют управлять спонтанным излучением у внедренных в матрицу структуры молекул или атомов. Начиная с работ Яблоновича [3] и Джона [4], концепция фотонных кристаллов стала одной из наиболее исследуемых в современной оптике. При наличии полной ФЗЗ распространение свет подавлено в любом направлении в спектральном диапазоне, совпадающем с запрещенной зоной. Данное свойство очень важно для возможных применений фотонных кристаллов в системах оптической связи и передачи информации, лазерной технике.
В первых теоретических работах изучались фотонные кристаллы, получаемые из непоглощающих и без-дисперсионных материалов [5]. В данных исследованиях был произведен поиск периодических структур имеющих полные ФЗЗ при высоких показателях преломления. На данный момент, наименьший показатель преломления, позволяющий существовать полной ФЗЗ, равен n =1,9 для алмазной решетки [6]. Это накладывает серьезные ограничения на выбор материала, т. к. в видимой области спектра не существует стекл и полимеров с таким показателем преломления. В дальнейших работах стали исследоваться материалы, обладающие поглощением и значительной дисперсией. В частности, фотонные кристаллы, состоящие из ионного материала или имеющие металлические включения. Используя метод конечных разностей, вычислены коэффициенты пропускания гранецентрированной кубической (ГЦК) и алмазных решеток, состоящих из идеально проводящих металлических шаров [7]. В результате в работе [7] было показано, что такая алмазная решетка имеет полную ФЗЗ размером более 45%, что является большим, чем у любого известного диэлектрического фотонного кристалла. Используя для диэлектрической проницаемости металлов приближение Друде, которое позволяет учитывать дисперсию и поглощение, установлено, что ГЦК решетка, состоящая из частиц благородных металлов (например серебра), размером порядка 160 нм, имеет большую полную
ФЗЗ [8]. Авторы объясняют это тем, что в области частот, в диапазоне которых образуется ФЗЗ, диэлектрическая проницаемость металлов принимает большие отрицательные значения, тем самым, образуя значительный контраст диэлектрических свойств, что является благоприятным для открытия полных ФЗЗ [1]. В работе [9] исследован диэлектрический волновод, покрытый с одной стороны одним слоем металлических наночастиц, упорядоченных в квадратную решетку. В результате, было обнаружено, что в такой структуре в оптическом диапазоне могут распространяться как волноводные, так и плазмонные моды.
Ионные материалы в инфракрасной области спектра имеют диапазон частот ю T < ю < ю L , для которого материал оптически подобен металлу, то есть диэлектрическая проницаемость отрицательна и имеет сильную дисперсию [10]. Фотонные кристаллы, полученные из ионного материала (поляритонные фотонные кристаллы) исследованы в работах [11,12]. Показано, что в результате фотон-фононного взаимодействия может образоваться поляритонная ФЗЗ, которую следует отличать от структурной ФЗЗ, образовывающейся в результате брэгговской дифракции собственных электромагнитных состояний на краю зоны Бриллюэна. ФЗЗ, возникающая в результате взаимодействия с коллективными оптическими возбуждениями, такими, как оптические фононы, плазмоны, экситоны, называется поляритонной ФЗЗ. В [13] обнаружен эффект слияния поляритонной и структурной ФЗЗ, который дает новый инструмент для получения структур с ФЗЗ.
Композитные среды с наночастицами благородных металлов представляют большой практический интерес при разработке различных оптических устройств. Линейные и нелинейные оптические свойства таких сред определяются плазмонным резонансом металлических наночастиц и свойствами прозрачной матрицы. Авторами [14,15] предсказано возникновение резонанса диэлектрической проницаемости в нанокомпозите, состоящем из металлических наночастиц, взвешенных в прозрачной матрице, причем положение резонанса зависит как от диэлектрической проницаемости исходных материалов, так и от концентрации наночастиц. Форма резонансов диэлектрической проницаемости такого нанокомпозита, совпадает с формой резонансов ионного материала, но резонанс лежит в области видимого света. Представляет большой интерес, как с прикладной, так и с фундаментальной точки зрения, использование таких нанокомпозитов в качестве материалов фотонных кристаллов. В нашей работе мы вычисляем коэффициенты пропускания, отражения, поглощения для одномерного фотонного кристалла, состоящего из нанокомпозита: металлические наночастицы, распределенные случайным образом в прозрачной матрице.
Для того чтобы найти диэлектрическую проницаемость нанокомпозита s mix( to ), используем формулу Максвелла-Гарнета:
S mix( to ) — S d = f БтИ -s d
Smix(to) + 2s d Sm(to) + 2s d
где f - относительный объем занимаемый наночастицами, s m ( to ) - диэлектрическая проницаемость металла, из которого изготовлены наночастицы, s d - диэлектрическая постоянная матрицы, в которую погружаются наночастицы, to - частота излучения.
Наночастицы распределены в матрице случайным образом, но однородно. Будем считать, что наночастицы имеют форму шара, с радиусом в пределах нескольких нанометров, что значительно меньше длины волны и глубины проникновения поля в материал. Диэлектрическую проницаемость металла, из которого изготовлены наночастицы, найдем, используя приближение Друде, в следующем виде:
S m( to ) = S 0
-
ω
p
to ( to + i y )
где s 0 - постоянная ( s 0 =5 для серебра), to p - плазменная частота ( to p = 9 эВ для серебра), у - релаксационная постоянная ( у = 0,02 эВ для серебра [16]). Для определенности, во всех дальнейших расчетах в качестве металла мы будем использовать серебро. Следует отметить, что соотношение (1) можно получить, если применить формулу Клаузиуса-Моссотти к расположенным в вакууме наночастицам с нормированной диэлектрической проницаемостью S m( to )/ s d [17]. Подставив (2) в (1), найдем S mix( to ) в виде:
S mix( to ) =S mx ( to ) + i S m ix ( to ) (3)
На рис. 1 представлены зависимости s mix ( to ) и s m ix ( to ) при f = 0,2, s d = 2,56. Можно увидеть, что кривые на рис. 1 имеют резонансный характер (вид кривых аналогичен случаю ионного материала [10]). Пренебрегая малым фактором у 2 , найдем, что функция s mix ( to ) обращается в ноль в точках:
to 10
=ω p
1 - f
S 0 + 2 s d - f ( S 0 - S d )
S 0( S 0 + 2 s d - f ( S 0 -S d )) toon = to„ ,1 +-- 20 p V s d ( S o + 2 S d + 2 f ( S o -s d ))
( to 10/ to p =0,288 и to 20/ to p =0,355, при f =0,2, s d =2,56). На промежутке [ to 10, to 20] функция s mix ( to ) принимает отрицательные значения, а значит, в этой области частот нанокомпозит оптически подобен металлу. Следовательно, можно ожидать появления поляритонных ФЗЗ в этом промежутке частот.
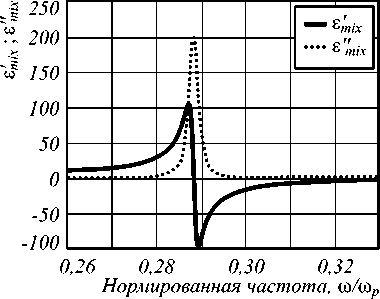
Рис. 1. Функции s mix ( to ) и s mix ( to ) для серебряных наночастиц, взвешенных в прозрачной матрице, при f =0,2, ε d =2,56
Рассмотрим одномерный фотонный кристалл, состоящий из N элементарных ячеек с периодом а . Каждая ячейка состоит из слоя толщиной d 1 с диэлектрической проницаемостью s mix ( to ) и слоя толщиной d 2 с диэлектрической проницаемостью равной 1. Период ячейки а равен a = d 1 + d 2. Во всех случаях рассматривается нормальное падение электромагнитной волны на фотонный кристалл. Для нахождения коэффициентов пропускания, отражения, поглощения использовался метод конечных разностей [18]. Коэффициенты пропускания и поглощения показаны на рис. 2, при N =16, f =0,2, d 1 / а = 0,5, а / X p =1. На графике частота указана в единицах плазменной частоты to p . На рис. 3 представлено изменение ФЗЗ в зависимости от размера элементарной ячейки а , при N =16, f =0,2, d 1 / а = 0,5 . Под ФЗЗ понимается такой диапазон частот, для которого коэффициент пропускания меньше 0,1.
На графике размер элементарной ячейки а отмечен в единицах плазменной длины волны X p , равной X p = 2 п c / to p , где c - скорость света в вакууме, а частота в единицах плазменной частоты to p . Пустыми кругами отмечается нижний край ФЗЗ, а закрашенными - верхний.
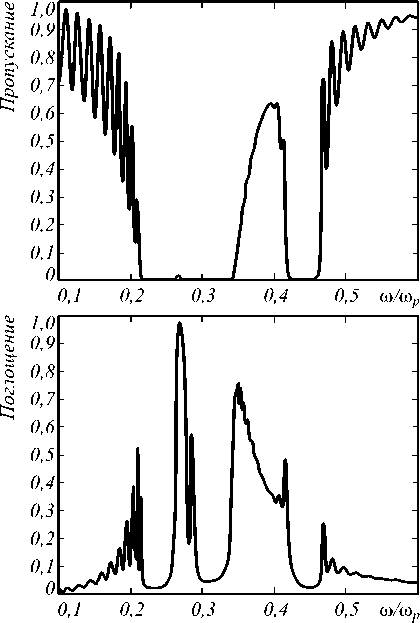
Рис. 2. Коэффициенты пропускания и поглощения
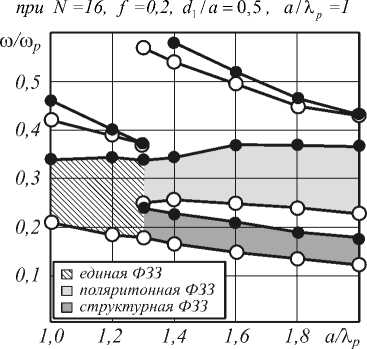
Рис. 3. Поведение ФЗЗ в зависимости от размера элементарной ячейки а при N =16, f =0,2, d 1 / a =0,5
На рис. 3 можно заметить, что при a / Xp =1,3 единая ФЗЗ расщепляется на поляритонную и структурную ФЗЗ. Для того, чтобы это доказать, необходимо исследовать поведение этих ФЗЗ при изменении фактора заполнения нанокомпозитом, т.е. при изменении отношения d 1 / a . Как показано в [13], поляритонная ФЗЗ увеличивается в размерах при увеличении фактора заполнения материалом, тогда как структурная ФЗЗ достигает максимума и начинает уменьшаться в размере. Изменение ФЗЗ при варьировании фактора заполнения нанокомпозитом представлено на рис. 4, при a / Xp =2. Можно наблюдать, что поляритонная ФЗЗ с центром между ю10 - ю20 увеличивается в размере, при увеличении отношения d 1 / a , тогда как структурная ФЗЗ, лежащая ниже, достигает максимума в размере и начинает уменьшаться. Эффект расщепления ФЗЗ на поляритонную и структурную дает нам новый инструмент в проектировании фотонных кристаллов. Данный эффект дает нам возможность, не меняя фактора заполнения нанокомпозитом, изменяя характерные размеры ячейки фотонного кристалла, кардинально изменять оптические свойства. В обычных диэлектрических фотонных кристаллах, меняя размеры ячейки (при постоянном факторе заполнения), мы только сдвигаем ФЗЗ, но не меняем
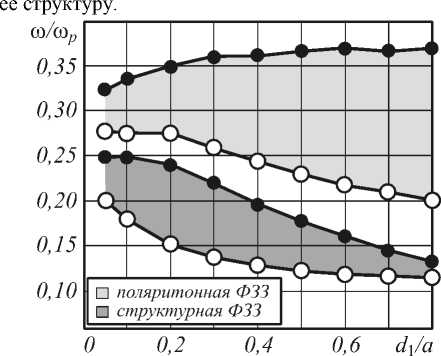
Рис. 4. Зависимость ФЗЗ от фактора заполнения нанокомпозитом d 1 / a при a / X p =2, N =16, f =0,2
Следует так же отметить, что, уменьшая концентрацию металлических наночастиц, мы понижаем поглощение в нанокомпозите. В металлических фотонных кристаллах поглощение очень существенно, вследствие высокой концентрации металла. Кроме того, металлические фотонные кристаллы достаточно сложно создать экспериментально, из-за необходимости периодически выстроить субмикронные металлические объекты. В исследуемом нанокомпозите металлические частицы распределены случайным образом, а однородность распределения в пространстве мы можем реализовать, используя кулоновское взаимодействие заряженных металлических шаров.
На рис. 5 показано изменение ФЗЗ в зависимости от концентрации металлических наночастиц f , при N =8, d 1 / a =0,5, a / X p =1. В следствие того, что с увеличением f ширина отрезка [ ю 10, ю 20] увеличивается, мы наблюдаем рост размера поляритонной ФЗЗ. Структурная ФЗЗ ведет себя более сложным образом, при f =0,15 она достигает максимального размера, затем уменьшается до нуля. Следует так же заметить, что центр структурной ФЗЗ перемещается в более высокие частоты, при увеличении f .
Противоположное поведение структурной ФЗЗ наблюдается при a / X p =2, что показано на рис. 6.
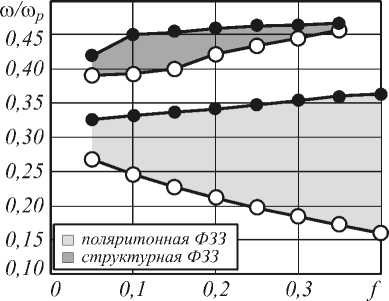
Рис. 5. Зависимость ФЗЗ от концентрации металлических наночастиц при f , при a/λp =1, N =8, d1 /a=0,5
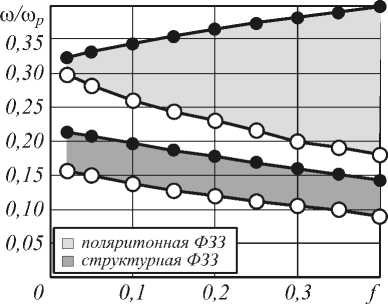
Рис. 6. Зависимость ФЗЗ от концентрации металлических наночастиц f при a / λ p =2, N =8, d 1 / a =0,5
В этом случае, при увеличении f структурная ФЗЗ практически не изменяется в размерах, причем ее центр смещается в более низкие частоты [14]. Данный эффект, зависимости поведения структурной ФЗЗ от ее положения относительно поляритонной ФЗЗ, может оказаться полезным при проектировании фотонных кристаллов с необходимыми свойствами. Изменяя концентрацию металлических наночастиц, мы можем добиться того, что ФЗЗ окажется в нужных частотах.
Возможность изменения параметра f выгодно отличает нанокомпозит от ионного материала. В ионных материалах положение пика резонанса нельзя изменять, что может негативно сказаться на возможностях производства фотонных кристаллов, из этих материалов. Также важно и то, что фотонные кристаллы на основе нанокомпозита, позволяют работать в видимом диапазоне частот.
Заключение
В данной работе исследовано поведение ФЗЗ при изменении размера элементарной ячейки и концентрации металлических наночастиц.
Предсказано возникновение эффекта расщепления единой ФЗЗ на поляритонную и структурную ФЗЗ.
Найдено различие в поведении структурной ФЗЗ при изменении концентрации металлических наночастиц, в зависимости от ее положения относительно поляритонной ФЗЗ. Рассмотренные эффекты позволяют расширить возможности создания новых фотонных кристаллов с заданными свойствами.


