Однопараметрическое распределение непрерывной случайной величины для моделирования отказов в технических системах

При моделировании сложных технических систем в ряде случаев возникают ситуации, в которых известные законы распределения случайных величин проявляют значительные ограничения [1; 2]. Пусть, например, необходимо определить долю отказавших объектов, находящихся на испытаниях [3; 4]. Если известны число объектов и вероятность отказов, то использование биномиального распределения легко решает указанный вопрос [5; 6]. Однако зачастую использование двухпараметрического распределения при решении прикладных задач, связанных с неопределенностью исходных данных, представляется весьма неудобным.

Сущность подхода

Представим, что на испытании находится совокупность некоторого числа N идентичных объектов (в общем случае N не определено). Случайная величина ^ˆη определяется долей оставшихся исправными объектов и лежит, таким образом, в интервале от 0 до 1. При этом вероятность p отказа отдельного объекта является, в свою очередь, не фиксированной в рамках испытания величиной, а случайной, что обусловлено необходимостью «разыгрывать» при моделировании неопределенность исходных данных о характере отказов [7; 8]. Для этого неопределенность вероятности p отказов будем учитывать следующим образом. При максимальной неопределенности она равномерно распределена от 0 до 1.

Терехов В.Г., Захаров И.В. Однопараметрическое распределение непрерывной...    41

При крайних значениях (0 или 1) параметра η искомого распределения оно должно вырождаться в соответствующий детерминизм случайной величины ^ˆη . В то же время математическое ожидание M [ п ] величины п должно иметь смысл ожидаемой вероятности отказа объекта M [ p ] , а при единственном объекте ( N = 1) искомое распределение должно вырождаться в распределение Бернулли с параметром p = η [1]. Поэтому биномиальное распределение не удовлетворяет данным требованиям, так как характеризуется «колоколообразной» плотностью распределения и при N →∞ очевидно ведет к детерминизму П ^ p = П, что не отражает смысл поставленной задачи. При этом оно двухпараметрическое, а неизвестны как число объектов, так и вероятность их отказов (известно лишь ее математическоеожидание M [ p ] = п).

Искомый закон распределения величины ˆη построим следующим образом. Представим, что объекты отказывают последовательно, причем отказ одного объекта уменьшает вероятность отказов других исходя из того, что фактор, вызывающий отказ объекта, воздействует как на исправные объекты, так и на уже отказавшие. Поэтому из соображения пропорциональности вероятности p числу объектов, остающихся исправными, примем, что ^ˆη определяется как дополнение до единицы функции показательного распределения ˆˆ

-z     A ln6     *А     _ А _____„______

= e = 6 , где Q — случайная вели-

V           V V                     Л У—X            А некоторой случайной величины z. Отсюда n = e

—

чина, равномерно распределенная от 0 до 1. Параметр A положим таким, чтобы 1 - п                                                             -9

M 1 П 1 = П- Тогда п = у ^п , функция распределения выразится как F ( x ) = x ¹ ~ⁿ , x е( 0;1 ] , 2П - 1                                         ¹

а плотность распределения f _n ( x ) = ^ П x ^{1 n} , x е( 0;1 ] .

Пример

Удобство предложенного распределения состоит в том, что оно, являясь однопараметрическим, при η = 0 и η = 1 сводит величину ˆη к детерминированной, а при η = 0,5 сводится к равномерному распределению. При этом отражен случайный характер степени воздействия фактора, вызывающего отказ некоторого количества объектов из их совокупности. Примеры графиков плотности распределения, соответствующие предложенному закону, показаны на рисунке. Изложенный подход использован на практике (см., например: [2]).

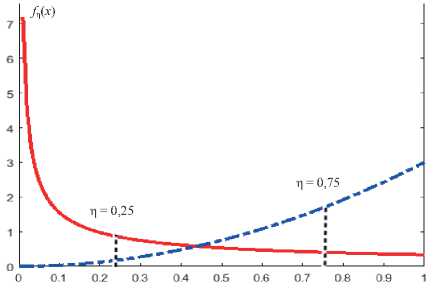
Примеры плотности распределения доли ˆη исправных объектов

42 в ыпуск 3/2019

Выводы

В условиях неопределенности исходных данных для анализа результатов моделирования сложных систем предпочтительным является использование однопараметрических распределений. Предложенное распределение можно в известном смысле рассматривать как «непрерывный однопараметрический аналог» биномиального и использовать при решении прикладных задач [9; 10].