Однородность магнитного поля систем правильных многоугольников с током
Автор: Фишбейн Л.А.
Журнал: Международный журнал гуманитарных и естественных наук @intjournal
Рубрика: Физико-математические науки
Статья в выпуске: 9-1 (84), 2023 года.
Бесплатный доступ
На основании закона Био-Савара-Лапласа получено выражение для магнитной индукции вдоль оси симметрии двух правильных эквивалентных осесимметричных произвольных многоугольников с током, а также условия обнуления второй производной в разложении в ряд Тейлора в центре системы. Показано, что такие системы обладают практически одинаковой однородностью магнитного поля.
Однородность магнитного поля, кольца гельмгольца, круглые, треугольные и квадратные витки с током (кольца)
Короткий адрес: https://sciup.org/170200383
IDR: 170200383 | DOI: 10.24412/2500-1000-2023-9-1-294-298
Текст научной статьи Однородность магнитного поля систем правильных многоугольников с током
Генерирование однородного магнитного поля является необходимым условием как для проведения многих физических и биологических экспериментов, так и для калибровки различных физических устройств. Наиболее часто для этих целей служат системы катушек с током, позволяющие достаточно легко поместить исследуемый объект в пространство с магнитным полем. В зависимости от назначения были разработаны различные конструкции систем катушек, отличающиеся друг от друга формой, количеством и пространственным расположением. Наиболее широко исследованы круглая и квадратная геометрия катушек в конфигурации Гельмгольца. В меньшей степени - треугольная и многоугольная геометрия.
В данной статье представлено сравнительное исследование однородности магнитного поля для круглых, квадратных, треугольных и шестиугольных катушек Гельмгольца вдоль оси симметрии.
Магнитное поле системы двух правильных многоугольников с током
Используя закон Био-Савара-Лапласа, рассчитаем магнитное поле осесимметричной системы двух правильных р -угольников (витков) со сторонами равными Ь, током I и лежащих в плоскостях, перпендикулярных оси симметрии и находящихся на одинаковом расстоянии l от центральной точки на оси z = 0. Ограничимся проекцией вектора магнитной индукции на ось z. В результате расчета получаем (рис. 1).
Bz(z) = р 1Ь- ctg - [----------------------1 +
-
- Р ((z + D2 + 4ctg2 -) ^С^У^^^^^
]■
((z — I)2 +brctg2 -) j(z — iy+^(1 + ctg2-)
Отметим, что при р ^ го и Ь ^ 0 (рЬ ^ 2nR) получается выражение для проекции магнитного поля двух круглых витков с током [1]
Bz(z) = ^-IR2 [--------1------- 3 +--------1------- 3 ] ■ (2)
-
2 L((z + l)2 + R2) 2 ((z - l)2 + R2) 2 J
Здесь R — радиус витков (колец).
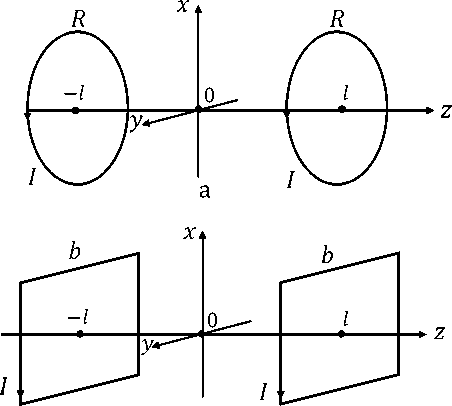
б
Рис. 1. Система двух соосных эквивалентных круглых (а) и квадратных (б) проводников с током
Введем безразмерные переменные и рассмотрим магнитное поле на оси в пространстве между двумя р -угольниками с током z b R
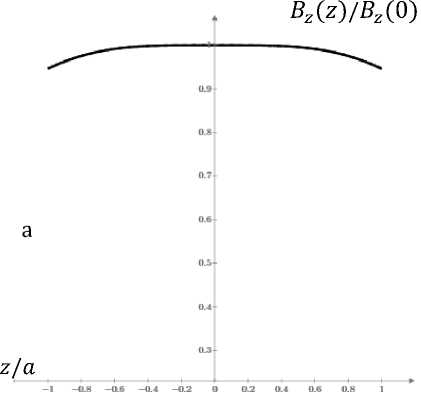
—1<1 Bz(z) = P5"jd'2ctg17V— 1 27 l р / z --------------------------- ■ + + 1)2 + d2ctg27) J(y+ 1)2 + d2 (1 + ctg2 77) ((f-D2 + Sz(0) = Bo = p—-d2ctg- 77 l р ]- — 1)2 + d2(1 + ctg27) (1 + d2ctg2 7) J1 + d2 (1 + ctg2P) В указанной области разложим в в центре системы (z = 0) выражение для проекции магнитной индукции в ряд Тейлора поz/l до четвертой степени. Очевидно, что нечетные степени в разложении зануляются, вследствие симметрии системы Тогда имеем Bz(z) = Bz(0) + 1d2Bz(0) 2 --7. L 2! dz2 + 1 d4Bz(0), z x z4 । 4! dz4Z Чем больше младших производных в разложении можно занулить, тем однороднее магнитное поле в центре системы. Пусть вторая производная от проекции вектора магнитной индукции (3) по z равна нулю. Получаем кубическое уравнение вида d6 (3ctg6 — + 5ctg4 — + 2ctg2 —) — d4 (6ctg4 — + 10ctg2 — + б) — d2 (21ctg2 — + 15) - 12 = 0 (5) Данное уравнение имеет аналитическое решение для произвольного р. В таблице 1 приведены численные значения d(p') для первых десяти правильных многоугольников (и окружности) и приведенный радиус описанной окружности г(р) для сравнения размеров этих многоугольников в поперечном направлении. Выражения (1,2) и значения таблицы 1 совпадают с аналитическими результатами работ [2, 3], где были рассмотрены круглые (р = го) , треугольные (р = 3) и квадратных (р = 4) многоугольники с током с учетом замены I = h/2,b = 2а, М =1 где h — расстояние между многоугольниками, 2 а —длина стороны многоугольников или диаметр окружности, М —число витков с током в каждом многоугольнике. При занулении второй производной разложение магнитной индукции в ряд Тейлора начинается с четвертой степени (не считая нулевой). Такие системы называются системами (кольцами) Гельмгольца [4]. Таблица 1. p d = b/2l r = Я/Z 3 3.060 3.534 4 1.837 2.597 5 1.370 2.331 6 1.107 2.213 7 0.924 2.150 8 0.808 2.112 9 0.714 2.087 10 0.639 2.069 го 0 2 Отметим, что в работе [3] для сравнения однородности магнитного поля систем круглых, треугольных и квадратных витков рассматриваются системы с одинаковыми сторонами 2 а, которые имеют приблизительно одинаковые поперечные, но разные продольные размеры, т.е. находят- ся на разном расстоянии h(a) друг от друга. Магнитное поле изучается на одном и том же отрезке вдоль оси z вокруг центральной точки z = 0. В результате имеем [3]: для круглых витков 32n5z0 /z йо^ Bz(z) = -^° [1 — 1,152 (-)4], h = a, BZO=^N, для треугольных витков 5 (z) =-----365z0 [1 — 6,0254 (Z)4] , h = 0,6536a, 1.3204V4.3204a va -I для квадратных витков 5z(z) = 165zo 1.2965V2.2965a [1 — 0,8068 (|)4], h = 1,0890a. Рис. 2. Распределение магнитного поля система двух соосных: a) квадратных (1), круглых (2) и треугольных (3) проводников с током имеющих одинаковые а длины сторон; б) квадратных (1), круглых (2) и треугольных (3) проводников с током находящихся на одинаковом расстоянии Z друг от друга. б z/Z На основании приведенных выше выражений и расчета, приведенного на рисунке 2а в работах делается вывод, что магнитное поле системы треугольников с током гораздо менее однородно, чем поле системы квадратов и круглых витков с током. Нам представляется более правильным другой подход. Сравним магнитные поля систем, имеющих одинаковые продольные размеры, т.е. находящихся на одинаковом расстоянии Z друг от друга, но разные поперечные. В результате имеем: для круглых витков Bz(z) = ^Ц [1—97 (Z)4] = ^ 0.3578[1 - 0,0720 (Z)4], Z 3 125 Z Z Z для треугольных витков Bz(z) = p0.3411[1 - 0,0687 (Z)4], для квадратных витков Bz(z) = ^-0.3528[1 — 0,0709 (Z)4], для шестиугольных витков Bz(z) = ^0-0.3567[1 - 0,0662 (Z)4], и т.д. Если на рис.2а для каждой из кривых ограничится интервалом по оси абсцисс h(a) --: а то мы получим по оси ординат значения аналогичные значениям, приведенным на рисунке 2б. Заключение На основании закона Био-Савара-Лапласа получено выражение, позволяю- z h(a) а — а , щее рассчитать магнитное поле вдоль оси симметрии систем Получено выражение, позволяющее. Таким образом, на основании полученных выше уравнений и расчетов, приведенных на рисунке 2б, можно сделать вывод о, практически, одинаковой однородности магнитных полей систем ком, имеющих одинаковые продольные правильных р - угольников (и колец) с то- размеры.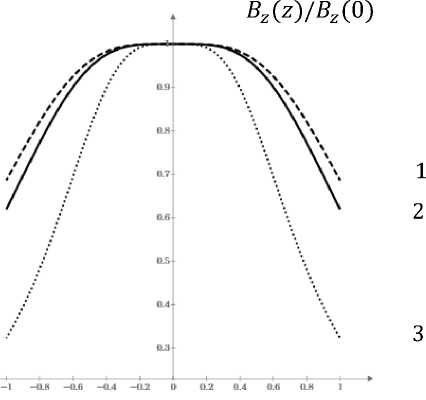
Список литературы Однородность магнитного поля систем правильных многоугольников с током
- Fishbein L. On the possibility of creating a magnetic field with a given degree of spatial inhomogeneity // Rev. Sci. Instrum. 92, 064705 (2021). DOI: 10.1063/5.0040871 EDN: LFZIVG
- D.M. Petkovic and M.D. Radi'c. Generalization of helmholtz coil 'problem // Serbian Journal of Electrical Engineering. - 2015. - Vol. 12, №3. - Pp. 375-384.
- Restrepo, A. F., Franco, E., Cadavid, H., & Pinedo, C. R. (2017). A comparative study of the magnetic field homogeneity for circular, square and equilateral triangular helmholtz coils // International Conference on Electrical, Electronics, Communication, Computer, and Optimization Techniques (ICEECCOT). DOI: 10.1109/iceeccot.2017.8284514
- Caprari R.S. Optimal current loop systems for producing uniform magnetic fields // Meas. Sci. Technol. - 1995. - №6. - P. 593. EDN: AZLQST


